5.2: Motores térmicos y el ciclo de Carnot
- Page ID
- 72392
Motores de Calor
Sadi Carnot (1796 — 1832) (Mendoza, 2016), un físico e ingeniero francés estaba muy interesado en la mejora de las máquinas de vapor para realizar las tareas que necesita la sociedad moderna.

Para simplificar su análisis del funcionamiento interno de un motor, Carnot ideó un constructo útil para examinar qué afecta la eficiencia del motor. Su construcción es el motor de calor. La idea detrás de un motor térmico es que tomará energía en forma de calor, y la transformará en una cantidad equivalente de trabajo.
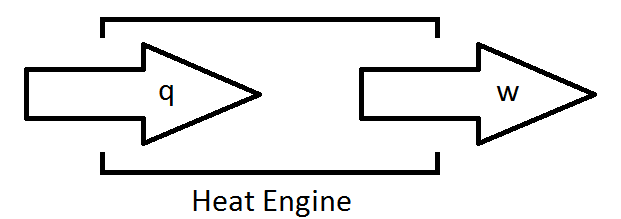
Desafortunadamente, tal dispositivo no es práctico. Resulta que la naturaleza impide la conversión completa de la energía en trabajo con una eficiencia perfecta. Esto lleva a una importante declaración de la Segunda Ley de la Termodinámica.
Es imposible convertir el calor en una cantidad equivalente de trabajo sin que ocurran otros cambios en el universo.
Como tal, una imagen más razonable del motor térmico es aquella que permitirá pérdidas de energía a los alrededores.
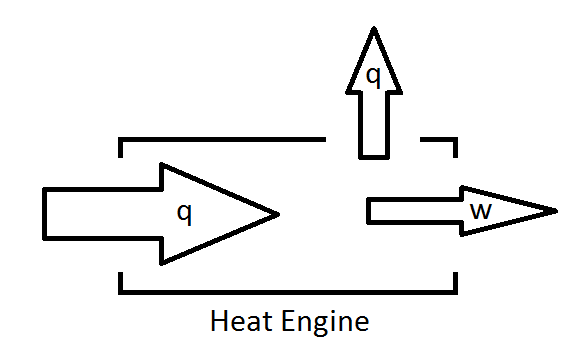
La fracción de energía suministrada al motor que se puede convertir a trabajo define la eficiencia del motor.
El ciclo del carnot
El ciclo Carnot es un motor térmico cíclico teórico que puede utilizarse para examinar lo que es posible para un motor para el que el trabajo es convertir calor en trabajo. Por simplicidad, toda la energía proporcionada al motor ocurre isotérmicamente (y reversiblemente) a una temperatura\(T_h\) y toda la energía perdida en el entorno también ocurre isotérmica y reversiblemente a temperatura\(T_l\). Para asegurar esto, el sistema debe cambiar entre las dos temperaturas adiabáticamente.
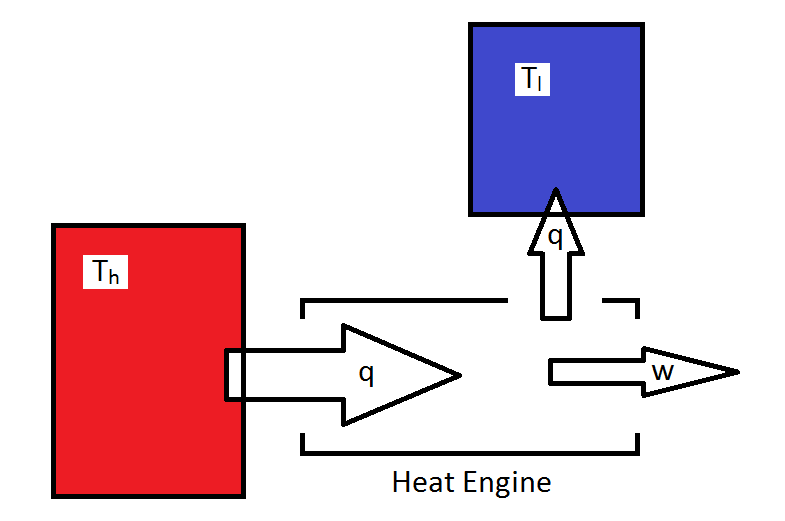
Así, el ciclo consta de cuatro patas reversibles, dos de las cuales son isotérmicas, y dos de las cuales son adiabáticas.
- Expansión isotérmica de p 1 y V 1 a p 2 y V 2 a T h.
- Expansión adiabática de p 2, V 2, T h a p 3, V 3, T l.
- Compresión isotérmica de p 3 y V 3 a p 4 y V 4 a T l.
- Compresión adiabática de p 4, V 4, T l a p 1, V 1, T h.
Trazado en un diagrama de presión-volumen, el ciclo Carnot se ve de la siguiente manera:
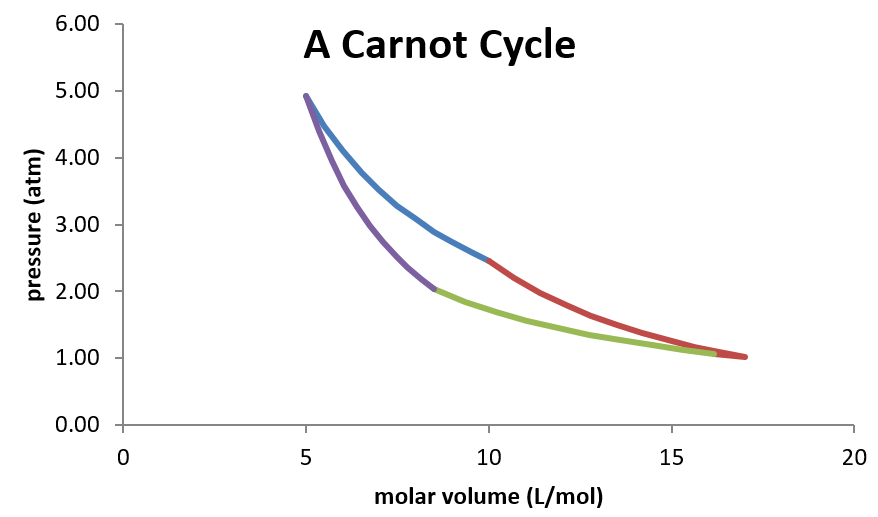
Debido a que este es un ciclo cerrado (el estado final es idéntico al estado inicial) cualquier función de estado debe tener un cambio neto de cero a medida que el sistema se mueve alrededor del ciclo. Además, la eficiencia del motor puede expresarse por la cantidad neta de trabajo que produce el motor por unidad de calor suministrada para alimentar el motor.
\[\epsilon = \dfrac{w_{net}}{q_h}\]
Para examinar esta expresión, es útil anotar expresiones del flujo de calor y trabajo en cada una de las cuatro patas del ciclo del motor.
| Pierna | Calor | Trabajo |
|---|---|---|
| I | q h = -nRT h ln (V 2 /V 1) | nRT h ln (V 2 /V 1) |
| II | 0 | C V (T l — T h) |
| III | q l = -nRT l ln (V 4 /V 3) | nRT l ln (V 4 /V 3) |
| IV | 0 | C V (T h — T l) |
La cantidad total de trabajo realizado viene dada por la suma de términos en la columna sed. Claramente los términos para las dos piernas adiabáticas cancelan (ya que tienen la misma magnitud, pero signos opuestos). Por lo que el trabajo total realizado viene dado por
\[ w_{tot} = nRT_h \ln \left( \dfrac{V_2}{V_1} \right) + nRT_l \ln \left( \dfrac{V_4}{V_3} \right) \]
La eficiencia del motor puede definirse como el trabajo total producido por unidad de energía proporcionada por el reservorio de alta temperatura.
\[\epsilon = \dfrac{w_{tot}}{q_h}\]
o
\[\epsilon = \dfrac{ nRT_h \ln \left( \dfrac{V_2}{V_1} \right) + nRT_l \ln \left( \dfrac{V_4}{V_3} \right)}{nRT_h \ln \left( \dfrac{V_2}{V_1} \right) } \label{eff1}\]
Esa expresión tiene muchas variables, pero resulta que se puede simplificar drásticamente. Resulta que por la elección de vías que conectan los estados se coloca una restricción muy importante sobre los valores relativos de V 1, V 2, V 3 y V 4. Para entender esto, debemos considerar cómo se relaciona el trabajo de expansión adiabática con las temperaturas y volúmenes iniciales y finales. En el Capítulo 3, se demostró que las temperaturas y volúmenes iniciales y finales de una expansión adiabática están relacionados por
\[V_iT_i^{C_V/R} = V_fT_f^{C_V/R}\]
o
\[ \dfrac{V_i}{V_f} = \left( \dfrac{T_f}{T_i} \right)^{C_V/R}\]
Usando las patas adiabáticas de expansión y compresión (II y IV), esto requiere que
\[\dfrac{V_2}{V_2} = \left( \dfrac{T_h}{T_l} \right)^{C_V/R}\]
y
\[\dfrac{V_4}{V_1} = \left( \dfrac{T_l}{T_h} \right)^{C_V/R}\]
Ya que los segundos términos son recíprocos el uno del otro, ¡los primeros términos deben ser también!
\[ \dfrac{V_2}{V_2}=\dfrac{V_1}{V_4}\]
Un simple reordenamiento demuestra que
\[ \dfrac{V_2}{V_1}=\dfrac{V_3}{V_4}\]
¡Esto es muy conveniente! Es lo que permite la simplificación de la expresión de eficiencia (Ecuación\ ref {eff1}) se convierte
\[\epsilon = \dfrac{ \cancel{nR}T_h \cancel{\ln \left( \dfrac{V_2}{V_1} \right)} + \cancel{nR}T_l \cancel{ \ln \left( \dfrac{V_2}{V_1} \right)}}{\cancel{nR}T_h \cancel{\ln \left( \dfrac{V_2}{V_1} \right)} }\]
Cancelación de términos en los rendimientos del numerador y denominador
\[\epsilon = \dfrac{T_g-T_l}{T_h} \label{eff2}\]
¡Esta expresión da la máxima eficiencia y depende solo de las altas y bajas temperaturas!
Además, cabe señalar que el motor térmico puede funcionar hacia atrás. Al proporcionar trabajo al motor, puede ser fuerzas para extraer calor del depósito de baja temperatura y disiparlo en el depósito de alta temperatura. Así es como funciona un refrigerador o bomba de calor. La eficiencia limitante de dicho dispositivo también se puede calcular utilizando las temperaturas de los depósitos fríos de lata caliente.
Ejemplo\(\PageIndex{1}\):
¿Cuál es la máxima eficiencia de un juego de congeladores para mantener el helado a un -10 o C fresco, que está operando en una habitación que es de 25 o C? ¿Cuál es la cantidad mínima de energía necesaria para sacar 1.0 J del congelador y disiparlo a la habitación?
Solución:
La eficiencia viene dada por la Ecuación\ ref {eff2} y convirtiendo las temperaturas a una escala absoluta, la eficiencia se puede calcular como
\[\epsilon = \dfrac{298\,K - 263\,K}{298\,K} \]
Este valor se puede utilizar de la siguiente manera
\[energy_{transferred} = \epsilon (work_{required})\]
Entonces
\[ 1.0 \,J = 0.1174(w)\]
o
\[w = 8.5\, J\]
Es interesante señalar que cualquier proceso cíclico cerrado arbitrario puede describirse como una suma de ciclos Carnot infinitesimalmente pequeños, por lo que todas las conclusiones alcanzadas para el ciclo Carnot se aplican a cualquier proceso cíclico.
Colaboradores
Patrick E. Fleming (Department of Chemistry and Biochemistry; California State University, East Bay)


