1.9: El principio de incertidumbre de Heisenberg
- Page ID
- 79529
- Para entender que en algún momento no se puede saber todo sobre un sistema cuántico como lo demuestra el principio de incertidumbre de Heisenberg.
En la física clásica, estudiar el comportamiento de un sistema físico suele ser una tarea sencilla debido a que varias cualidades físicas se pueden medir simultáneamente. Sin embargo, esta posibilidad está ausente en el mundo cuántico. En 1927 el físico alemán Werner Heisenberg describió limitaciones como el Principio de Incertidumbre de Heisenberg, o simplemente el Principio de Incertidumbre, afirmando que no es posible medir tanto el impulso como la posición de una partícula simultáneamente.
El Principio de Incertidumbre de Heisenberg es una teoría fundamental en la mecánica cuántica que define por qué un científico no puede medir múltiples variables cuánticas simultáneamente. Hasta los albores de la mecánica cuántica, se sostuvo como un hecho que todas las variables de un objeto podían conocerse con precisión exacta simultáneamente para un momento dado. La física newtoniana no puso límites a cómo mejores procedimientos y técnicas podrían reducir la incertidumbre de medición de manera que era concebible que con el cuidado y precisión adecuados se pudiera definir toda la información. Heisenberg hizo la audaz proposición de que hay un límite inferior a esta precisión haciendo que nuestro conocimiento de una partícula sea inherentemente incierto.
Probabilidad
La materia y los fotones son olas, lo que implica que se extienden a cierta distancia. ¿Cuál es la posición de una partícula, como un electrón? ¿Está en el centro de la ola? La respuesta radica en cómo se mide la posición de un electrón. Los experimentos muestran que encontrarás el electrón en algún lugar definido, a diferencia de una onda. Pero si configuras exactamente la misma situación y la vuelves a medir, encontrarás el electrón en una ubicación diferente, a menudo lejos de cualquier incertidumbre experimental en tu medición. Las mediciones repetidas mostrarán una distribución estadística de ubicaciones que aparecen como ondas (Figura 1.9.1 ).
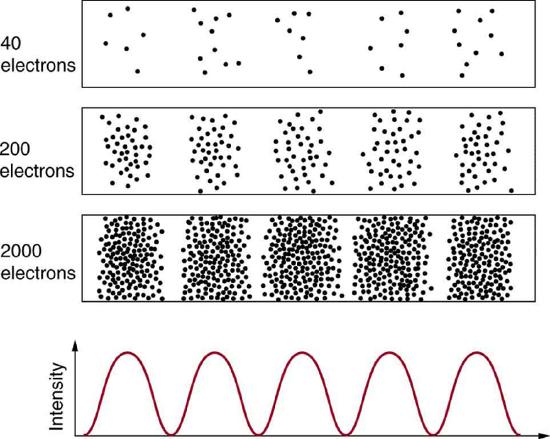
Después de que de Broglie propusiera la naturaleza ondulada de la materia, muchos físicos, entre ellos Schrödinger y Heisenberg, exploraron las consecuencias. Rápidamente surgió la idea de que, por su carácter de onda, la trayectoria y el destino de una partícula no pueden predecirse con precisión para cada partícula individualmente. Sin embargo, cada partícula va a un lugar definido (Figura 1.9.1 ). Después de compilar suficientes datos, obtiene una distribución relacionada con la longitud de onda y el patrón de difracción de la partícula. Existe cierta probabilidad de encontrar la partícula en una ubicación determinada, y el patrón general se denomina distribución de probabilidad. Quienes desarrollaron la mecánica cuántica idearon ecuaciones que predijeron la distribución de probabilidad en diversas circunstancias.
Es algo inquieto pensar que no se puede predecir exactamente a dónde irá una partícula individual, o incluso seguirla hasta su destino. Exploremos lo que sucede si tratamos de seguir una partícula. Considere los patrones de doble rendija obtenidos para electrones y fotones en la Figura 1.9.2 . Los patrones de interferencia se acumulan estadísticamente a medida que las partículas individuales caen sobre el detector. Esto se puede observar para fotones o electrones, por ahora, concentrémonos en los electrones. Se podría imaginar que los electrones están interfiriendo entre sí como cualquier onda lo hace. Para probar esto, se puede bajar la intensidad hasta que nunca haya más de un electrón entre las rendijas y la pantalla. ¡Se acumula el mismo patrón de interferencia!
Esto implica que la distribución de probabilidad de una partícula abarca ambas rendijas, y las partículas realmente interfieren consigo mismas. ¿Significa esto también que el electrón pasa por ambas hendiduras? Un electrón es una unidad básica de materia que no es divisible. Pero es una pregunta justa, y entonces deberíamos mirar para ver si el electrón atraviesa una hendidura o la otra, o ambas. Una posibilidad es tener bobinas alrededor de las ranuras que detecten cargas que se mueven a través de ellas. Lo que se observa es que un electrón siempre pasa por una hendidura u otra; no se divide para pasar por ambas.
Pero hay una trampa. Si determina que el electrón pasó por una de las hendiduras, ya no obtiene un patrón de doble rendija, sino que obtiene interferencia de una sola hendidura. No hay escape al usar otro método para determinar por qué hendidura pasó el electrón. Saber que la partícula pasó por una hendidura obliga a un patrón de una sola rendija. Si no observas por qué hendidura pasa el electrón, obtienes un patrón de doble rendija. ¿Cómo cambia el patrón saber por qué hendidura pasó el electrón? La respuesta es fundamentalmente importante: la medición afecta al sistema que se observa. Se puede perder información, y en algunos casos es imposible medir dos cantidades físicas simultáneamente con precisión exacta. Por ejemplo, se puede medir la posición de un electrón en movimiento dispersando luz u otros electrones de él. Esas sondas tienen ímpetu ellas mismas, y al dispersarse del electrón, cambian su impulso de una manera que pierde información. Hay un límite para el conocimiento absoluto, incluso en principio.
Principio de incertidumbre de Heisenberg
Es matemáticamente posible expresar la incertidumbre que, concluyó Heisenberg, siempre existe si se intenta medir el impulso y la posición de las partículas. Primero, debemos definir la variable “x” como la posición de la partícula, y definir “p” como el momento de la partícula. Se sabe que el momento de un fotón de luz es simplemente su frecuencia, expresada por la relación\(h/λ\), donde h representa la constante de Planck y\(\lambda\) representa la longitud de onda del fotón. La posición de un fotón de luz es simplemente su longitud de onda (\(\lambda\)). Para representar el cambio finito en las cantidades, la letra griega mayúscula delta, o Δ, se coloca delante de la cantidad. Por lo tanto,
\[\Delta{p}=\dfrac{h}{\lambda} \label{1.9.1} \]
\[\Delta{x}= \lambda \label{1.9.2} \]
Al sustituir\(\Delta{x}\)\(\lambda\) en Ecuación\(\ref{1.9.1}\), derivamos
\[\Delta{p}=\dfrac{h}{\Delta{x}} \label{1.9.3} \]
o,
\[\underset{\text{early form of uncertainty principle }}{\Delta{p}\Delta{x}=h} \label{1.9.4} \]
La ecuación se\(\ref{1.9.4}\) puede derivar asumiendo que la partícula de interés se está comportando como una partícula, y no como una onda. Simplemente deja\(\Delta p=mv\), y\(Δx=h/(m v)\) (de la expresión de De Broglie para la longitud de onda de una partícula). Sustituir\(Δp\) por\(mv\) en la segunda ecuación lleva a Ecuación\(\ref{1.9.4}\).
La ecuación\ ref {1.9.4} fue refinada aún más por Heisenberg y su colega Niels Bohr, y finalmente fue reescrita como
\[\Delta{p_x}\Delta{x} \ge \dfrac{h}{4\pi} = \dfrac{\hbar}{2} \label{1.9.5} \]
con\(\hbar = \dfrac{h}{2\pi}= 1.0545718 \times 10^{-34}\; m^2 \cdot kg / s\).
La ecuación\(\ref{1.9.5}\) revela que cuanto más precisa se conoce la posición de una partícula (cuanto más pequeña\(Δx\) es), menos precisión se conoce el momento de la partícula en la dirección x (\(Δp_x\)). Matemáticamente, esto ocurre porque cuanto más pequeño\(Δx\) se vuelve, más grande\(Δp_x\) debe llegar a ser para satisfacer la desigualdad. Sin embargo, cuanto más preciso se conoce el momento, la posición con menor precisión se conoce (Figura 1.9.2 ).
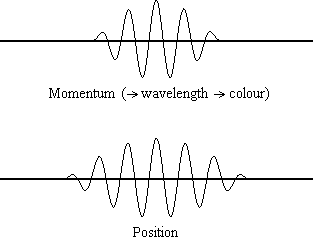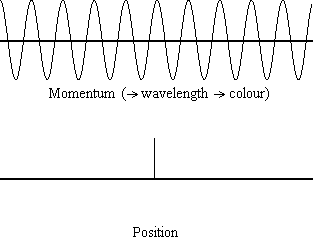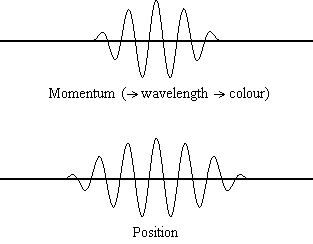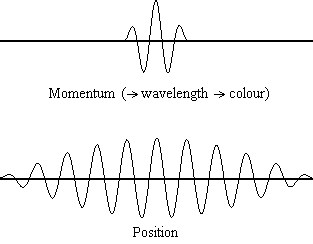
\(\ref{1.9.5}\)La ecuación relaciona la incertidumbre de impulso y posición. Una pregunta inmediata que surge es si\(\Delta x\) representa el rango completo de\(x\) valores posibles o si es la mitad (e.g.,\(\langle x \rangle \pm \Delta x\)). \(\Delta x\)es la desviación estándar y es una medida estadística de la dispersión de\(x\) valores. El uso de la mitad del rango posible es una estimación más precisa de\(\Delta x\). Como demostraremos más adelante, una vez construimos una función de onda para describir el sistema, entonces ambas\(x\) y se\(\Delta x\) pueden derivar explícitamente. Sin embargo por ahora, la Ecuación\ ref {1.9.5} funcionará.
Por ejemplo: Si un problema argumenta que una partícula está atrapada en una caja de longitud\(L\), entonces la incertidumbre de su posición es\(\pm L/2\). Entonces el valor de\(\Delta x\) usado en Ecuación\(\ref{1.9.5}\) debería ser\(L/2\), no\(L\).
Un electrón está confinado al tamaño de un átomo de magnesio con un radio de 150pm. ¿Cuál es la incertidumbre mínima en su velocidad?
Solución
El principio de incertidumbre (Ecuación\(\ref{1.9.5}\)):
\[\Delta{p}\Delta{x} \ge \dfrac{\hbar}{2} \nonumber \]
se puede escribir
\[\Delta{p} \ge \dfrac{\hbar}{2 \Delta{x}} \nonumber \]
y sustituyendo\(\Delta p=m \Delta v \) ya que la masa no es incierta.
\[\Delta{v} \ge \dfrac{\hbar}{2\; m\; \Delta{x}} \nonumber \]
los parámetros relevantes son
- masa de electrón\(m=m_e= 9.109383 \times 10^{-31}\; kg\)
- incertidumbre en la posición:\(\Delta x=150 \times 10^{-12} m \)
\[ \begin{align*} \Delta{v} &\ge \dfrac{1.0545718 \times 10^{-34} \cancel{kg} m^{\cancel{2}} / s}{(2)\;( 9.109383 \times 10^{-31} \; \cancel{kg}) \; (150 \times 10^{-12} \; \cancel{m}) } \\[4pt] &= 3.9 \times 10^5\; m/s \end{align*} \nonumber \]
¿Cuál es la máxima incertidumbre de velocidad del electrón descrita en el Ejemplo 1.9.1 ?
- Contestar
-
Infinito. No hay límite en la incertidumbre máxima, solo la incertidumbre mínima.
Comprensión del principio de incertidumbre a través de paquetes de ondas y el experimento de hendidura
Es difícil para la mayoría de la gente aceptar el principio de incertidumbre, porque en la física clásica la velocidad y la posición de un objeto se pueden calcular con certeza y precisión. Sin embargo, en la mecánica cuántica, la dualidad onda-partícula de los electrones no nos permite calcular con precisión tanto el momento como la posición porque la onda no está en una ubicación exacta sino que se extiende por el espacio. Un “paquete de ondas” se puede utilizar para demostrar cómo se puede calcular con precisión el impulso o la posición de una partícula, pero no ambas simultáneamente. Una acumulación de ondas de longitudes de onda variables se puede combinar para crear una longitud de onda promedio a través de un patrón de interferencia: esta longitud de onda promedio se llama el “paquete de ondas”. Cuantas más ondas se combinan en el “paquete de ondas”, más precisa se vuelve la posición de la partícula y más incierto se vuelve el impulso porque se agregan más longitudes de onda de momentos variables. Por el contrario, si queremos un impulso más preciso, agregaríamos menos longitudes de onda al “paquete de ondas” y entonces la posición se volvería más incierta. Por lo tanto, no hay forma de encontrar simultáneamente tanto la posición como el impulso de una partícula.
Varios científicos han debatido el Principio de Incertidumbre, entre ellos Einstein. Einstein creó un experimento de hendidura para intentar desmentir el Principio de Incertidumbre. Tenía luz pasando por una hendidura, lo que provoca una incertidumbre de impulso porque la luz se comporta como una partícula y una onda a medida que pasa por la hendidura. Por lo tanto, se desconoce el impulso, pero se conoce la posición inicial de la partícula. Aquí hay un video que demuestra partículas de luz que pasan a través de una hendidura y a medida que la hendidura se hace más pequeña, la matriz final posible de direcciones de las partículas se vuelve más ancha. A medida que la posición de la partícula se vuelve más precisa cuando se estrecha la hendidura, la dirección, o por lo tanto el momento, de la partícula se vuelve menos conocida como se ve por una distribución horizontal más amplia de la luz.
La velocidad de un proyectil de 1.0 g es conocida por dentro\(10^{-6}\;m/s\).
- Calcular la incertidumbre mínima en su posición.
- ¿Cuál es la máxima incertidumbre de su posición?
Solución
a
De la ecuación\(\ref{1.9.5}\), el\(\Delta{p_x} = m \Delta v_x\) con\(m=1.0\;g\). Resolviendo\(\Delta{x}\) para obtener
\[ \begin{align*} \Delta{x} &= \dfrac{\hbar}{2m\Delta v} \\[4pt] &= \dfrac{1.0545718 \times 10^{-34} \; m^2 \cdot kg / s}{(2)(0.001 \; kg)(10^{-6} \;m/s)} \\[4pt] &= 5.3 \times 10^{-26} \,m \end{align*} \nonumber \]
Esto despreciable para todos los efectos y propósitos como se esperaba para cualquier objeto macroscópico.
b
Ilimitado (o el tamaño del universo). Los principios de incertidumbre de Heisenberg no cuantifican la incertidumbre máxima.
Estimar la incertidumbre mínima en la velocidad de un electrón confinado a un átomo de hidrógeno dentro de un diámetro de\(1 \times 10^{-10} m\)?
- Contestar
-
Necesitamos cuantificar la incertidumbre del electrón en posición. Podemos estimar eso como\(\pm 5 \times 10^{-10} m\). Por lo tanto, sustituyendo los números relavantes en Ecuación\ ref {1.9.5} y resolviendo para\(\Delta v\) obtenemos
\[\Delta v= 1.15 \times 10^6\, km/s \nonumber \]
Observe que la incertidumbre es significativamente mayor para el electrón en un átomo de hidrógeno que en el átomo de magnesio (Ejemplo 1.9.1 ) como se esperaba ya que el átomo de magnesio es apreciablemente mayor.
El principio de incertidumbre de Heisenberg no solo ayudó a dar forma a la nueva escuela de pensamiento conocida hoy en día como mecánica cuántica, sino que también ayudó a desacreditar teorías más antiguas. Lo más importante, el Principio de Incertidumbre de Heisenberg hizo evidente que había un error fundamental en el modelo Bohr del átomo. Dado que la posición y el impulso de una partícula no se pueden conocer simultáneamente, la teoría de Bohr de que el electrón viajaba en una trayectoria circular de un radio fijo orbitando el núcleo era obsoleta. Además, el principio de incertidumbre de Heisenberg, cuando se combina con otras teorías revolucionarias de la mecánica cuántica, ayudó a dar forma a la mecánica de las olas y a la comprensión científica actual del átomo.
- Heisenberg es parado por exceso de velocidad por la policía. El oficial le pregunta “¿Sabes lo rápido que ibas?”
- Heisenberg responde: “¡No, pero sabemos exactamente dónde estamos!”
- El oficial lo mira confundido y dice “¡ibas 108 millas por hora!”
- Heisenberg levanta los brazos y grita: “¡Genial! ¡Ahora estamos perdidos!”
Colaboradores y Atribuciones
- Sarah Woods, Kris Baumgartner (UC Davis)

