1.8: La teoría de Bohr del átomo de hidrógeno
- Page ID
- 79500
- Introducir los fundamentos detrás del átomo de Bohr y demostrar que puede predecir la ecuación de Rydberg para el espectro atómico del hidrógeno
Átomo planetario fallido de Rutherford
Ernest Rutherford había propuesto un modelo de átomos basado en los experimentos\(\alpha\) de dispersión de partículas de Hans Geiger y Ernest Marsden. En estos experimentos se dispararon núcleos de helio (\(\alpha\)-partículas) en finas láminas metálicas de oro. La mayoría de las partículas no se dispersaron; pasaron sin cambios a través de la delgada lámina metálica. Algunos de los pocos que estaban dispersos estaban dispersos en la dirección hacia atrás; es decir, retrocedieron. Esta dispersión hacia atrás requiere que la lámina contenga partículas pesadas. Cuando una\(\alpha\) -partícula golpea una de estas partículas pesadas simplemente retrocede, al igual que una bola arrojada a una pared de ladrillos. Dado que la mayoría de las partículas α no se dispersan, las partículas pesadas (los núcleos de los átomos) deben ocupar solo una región muy pequeña del espacio total del átomo. La mayor parte del espacio debe estar vacío u ocupado por partículas de muy baja masa. Estas partículas de baja masa son los electrones que rodean el núcleo.
Hay algunos problemas básicos con el modelo Rutherford. La fuerza Coulomb que existe entre partículas de carga opuesta significa que un núcleo positivo y electrones negativos deben atraerse entre sí, y el átomo debe colapsar. Para evitar el colapso, se postuló que el electrón estaba orbitando el núcleo positivo. La fuerza Coulomb (discutida a continuación) se utiliza para cambiar la dirección de la velocidad, así como una cuerda tira de una bola en una órbita circular alrededor de tu cabeza o la fuerza gravitacional mantiene a la luna en órbita alrededor de la Tierra. El origen de esta hipótesis que sugiere que esta perspectiva es plausible es la similitud de la gravedad y las interacciones culombicas. La expresión de la fuerza de gravedad entre dos masas (Ley de la gravedad de Newton) es
\[F_{gravity} \propto \dfrac{m_1m_2}{r^2}\label{1.8.1} \]
con\(m_1\) y\(m_2\) representando la masa del objeto 1 y 2, respectivamente y\(r\) representando la distancia entre los centros de los objetos
La expresión de la fuerza de Coulomb entre dos especies cargadas es
\[F_{Coulomb} \propto \dfrac{Q_1Q_2}{r^2}\label{1.8.2} \]
con\(Q_1\) y\(Q_2\) representando la carga del objeto 1 y 2, respectivamente y\(r\) representando la distancia entre los centros de los objetos.
Sin embargo, esta analogía también tiene un problema. Un electrón dando vueltas en círculo se acelera constantemente porque su vector de velocidad está cambiando. Una partícula cargada que se está acelerando emite radiación. Esta propiedad es esencialmente cómo funciona un transmisor de radio. Una fuente de alimentación impulsa electrones arriba y abajo de un cable y así transmite la energía (radiación electromagnética) que capta tu receptor de radio. La radio luego reproduce para ti la música que está codificada en la forma de onda de la energía radiada.
Si el electrón en órbita está generando radiación, está perdiendo energía. Si una partícula en órbita pierde energía, el radio de la órbita disminuye. Para conservar el momento angular, la frecuencia del electrón en órbita aumenta. La frecuencia aumenta continuamente a medida que el electrón colapsa hacia el núcleo. Dado que la frecuencia del electrón giratorio y la frecuencia de la radiación que se emite son las mismas, ambas cambian continuamente para producir un espectro continuo y no las líneas discretas observadas. Además, si uno calcula cuánto tiempo tarda en ocurrir este colapso, uno encuentra que tarda unos\(10^{‑11}\) segundos. Esto significa que nada en el mundo basado en la estructura de los átomos podría existir por más de unos\(10^{-11}\) segundos. Claramente algo está terriblemente mal con este cuadro clásico, lo que significa que algo faltaba en ese momento de las conocidas leyes de la física.
Una fuerza conservadora depende únicamente de la posición del objeto. Si una fuerza es conservadora, es posible asignar un valor numérico para el potencial en cualquier punto. Cuando un objeto se mueve de una ubicación a otra, la fuerza cambia la energía potencial del objeto en una cantidad que no depende del camino tomado. El potencial se puede construir como derivadas simples para las fuerzas 1-D:
\[F = -\dfrac{dV}{dx} \nonumber \]
o como gradientes en fuerzas 3-D
\[F = -\nabla V \nonumber \]
donde\(\nabla\) está el vector de derivados parciales
\[\nabla = \left ( \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right) \nonumber \]
Las fuerzas conservadoras más familiares son la gravedad y las fuerzas columbicas.
La ley de fuerza de Coulomb (Ecuación\(\ref{1.8.2}\)) proviene del correspondiente potencial de Coulomb (a veces llamado potencial electrostático)
\[V(r)=\dfrac{kQ_1 Q_2}{r} \label{1.8.5} \]
y se puede verificar fácilmente que la fuerza coulómbica de esta interacción (\(F(r)\)) es
\[F(r)=-\dfrac{dV}{dr} \label{1.8.6} \]
Como\(r\) es variado, la energía va a cambiar, por lo que tenemos un ejemplo de una curva de energía potencial\(V(r)\) (Figura\(\PageIndex{2; left}\)). Si\(Q_1\) y\(Q_2\) son el mismo signo, entonces la curva que es un potencial puramente repulsivo, es decir, la energía aumenta monótonamente a medida que las cargas se juntan y disminuye monótonamente a medida que se separan. A partir de esto, es fácil ver que cargas similares (cargas de la misma señal) se repelen entre sí.
Si las cargas son de signo opuesto, entonces la curva aparece aproximadamente Figura\(\PageIndex{2; right}\) y esto es un potencial puramente atractivo. Así, la energía disminuye a medida que se juntan las cargas, lo que implica que las cargas opuestas atraen
El modelo Bohr
Se observa que los espectros lineales discutidos en las secciones anteriores muestran que los átomos de hidrógeno absorben y emiten luz solo a longitudes de onda discretas. Esta observación está conectada a la naturaleza discreta de las energías permitidas de un sistema mecánico cuántico. La mecánica cuántica postula que, a diferencia de la mecánica clásica, la energía de un sistema sólo puede asumir ciertos valores discretos. Esto nos deja con la pregunta: ¿Cómo determinamos cuáles son estos valores de energía discreta permitidos? Después de todo, parece que la fórmula de Planck para las energías permitidas salió de la nada.
El modelo que describiremos aquí, debido a Niels Bohr en 1913, es un intento temprano de predecir las energías permitidas para los átomos de un solo electrón como\(\ce{H}\),,\(\ce{He^{+}}\),\(\ce{Li^{2+}}\)\(\ce{Be^{3+}}\), etc. Aunque el razonamiento de Bohr se basa en conceptos clásicos y por lo tanto, no es una explicación correcta, el razonamiento es interesante, por lo que examinamos este modelo por su significación histórica.
Considera un núcleo con carga\(+Ze\) y un electrón orbitando el núcleo. En este análisis, utilizaremos otra representación de la constante\(k\) en la ley de Coulomb (Ecuación\(\ref{1.8.5}\)), que se representa más comúnmente en la forma:
\[k=\dfrac{1}{4\pi \epsilon_0} \label{1.8.7} \]
donde\(\epsilon_0\) se conoce como la permitividad del espacio libre con el valor numérico\(\epsilon_0 = 8.8541878\times 10^{-12} \ C^2 J^{-1} m^{-1}\).
La energía total del electrón (se supone que el núcleo está fijo en el espacio en el origen) es la suma de energías cinéticas y potenciales:
\[E_{total}=\underset{\text{kinetic energy}}{\dfrac{p^2}{2m_e}} - \underset{\text{potential energy}}{\dfrac{Ze^2}{4\pi \epsilon_0 r}} \nonumber \]
La fuerza sobre el electrón es
\[\vec{F}=-\dfrac{Ze^2}{4\pi \epsilon_0 r^3}r \nonumber \]
y su magnitud es
\[F=|\vec{F}|=\dfrac{Ze^2}{4\pi \epsilon_0 r^3}|r|=\dfrac{Ze^2}{4\pi \epsilon_0 r^2} \nonumber \]
ya que\(\vec{F}=m_e \vec{a}\), la magnitud, se deduce que\(|\vec{F}|=m_e |\vec{a}|\). Si asumimos que la órbita es circular, entonces la aceleración es puramente centrípeta, entonces
\[|a|=\dfrac{v^2}{r} \nonumber \]
donde\(v\) está la velocidad del electrón. Equiparando la fuerza\(|F|\) a\(m_e |a|\), obtenemos
\[\dfrac{Ze^2}{4\pi \epsilon_0 r^2}=m_e\dfrac{v^2}{r} \nonumber \]
o
\[\dfrac{Ze^2}{4\pi \epsilon_0}=m_e v^2 r \nonumber \]
o
\[\dfrac{Ze^2 m_e r}{4\pi \epsilon_0}=(m_e vr)^2 \label{1.8.14} \]
La razón para escribir la ecuación de esta manera es que la cantidad\(m_e vr\) es el momento angular orbital clásico del electrón. Bohr estaba familiarizado con la teoría de Maxwell del electromagnetismo clásico y sabía que en una teoría clásica, el electrón orbitante debería irradiar energía y eventualmente colapsar en el núcleo (Figura 1.8.1 ). Él eludió este problema siguiendo la idea de Planck subyacente a la radiación de cuerpo negro y postulando que el momento angular orbital\(m_e vr\) del electrón solo podía tomar valores específicos
\[m_e vr=n\hbar\label{1.8.15} \]
con\(n=1,2,3,...\).
Tenga en cuenta que el electrón debe estar en movimiento, por lo que no\(n=0\) está permitido.
Sustituyendo la ecuación\(\ref{1.8.15}\) en la ecuación\(\ref{1.8.14}\), encontramos
\[\dfrac{Ze^2 m_e r}{4\pi \epsilon_0}=n^2 (\hbar)^2 \label{1.8.16} \]
La ecuación\ ref {1.8.16} implica que las órbitas solo podrían tener ciertos radios permitidos
\[\begin{align}r_n &= \dfrac{4\pi \epsilon_0 \hbar^2}{Ze^2 m_e}n^2 \\ &=\dfrac{a_0}{Z}n^2 \label{1.8.16B} \end{align} \]
con\(n=1,2,3,...\). L a colección de constantes se ha definido como\(a_0\)
\[a_0=\dfrac{4\pi \epsilon_0 \hbar^2}{e^2 m_e} \label{1.8.17} \]
una cantidad que se conoce como th e radio de Bohr.
También podemos calcular los momentos permitidos desde\(m_e vr=n\hbar\), y\(p=m_e v\). Por lo tanto,
\[\begin{align}p_n r_n &=n\hbar\\[4pt] p_n &=\dfrac{n\hbar}{r_n}\\[4pt] &=\dfrac{\hbar Z}{a_0 n} \\[4pt] &= \dfrac{Ze^2 m_e}{4\pi \epsilon_0 \hbar n}\end{align} \label{1.8.18} \]
Desde\(p_n\) y\(r_n\), podemos calcular las energías permitidas a partir de
\[E_n=\dfrac{p^2_n}{2m_e}-\dfrac{Ze^2}{4\pi \epsilon_0 r_n} \label{1.8.19} \]
Sustituir en las expresiones\(p_n\) y\(r_n\) y simplificar da
\[E_n=-\dfrac{Z^2 e^4 m_e}{32\pi^2 \epsilon_{0}^{2}\hbar^2}\dfrac{1}{n^2}=-\dfrac{e^4 m_e}{8 \epsilon_{0}^{2}h^2}\dfrac{Z^2}{n^2} \label{1.8.20} \]
W e puede redefinir una nueva escala de energía definiendo el Rydberg como
\[1 \ Ry = \dfrac{e^4 m_e}{8\epsilon_{0}^{2} h^2} =2.18\times 10^{-18} \ J. \nonumber \]
y esto simplifica las energías permitidas predichas por el modelo de Bohr (Ecuación\ ref {1.8.20}) como
\[E_n=-(2.18\times 10^{-18})\dfrac{Z^2}{n^2} \ J=-\dfrac{Z^2}{n^2} \ R_y \label{1.8.21} \]
De ahí que también se cuantifique la energía del electrón en un átomo. La ecuación\(\ref{1.8.21}\) da las energías de los estados electrónicos del átomo de hidrógeno. Es muy útil en el análisis de espectros para representar gráficamente estas energías en un diagrama de niveles de energía. Un diagrama de nivel de energía tiene la energía trazada en el eje vertical con una línea horizontal dibujada para ubicar cada nivel de energía (Figura 1.8.4 ).
Estos resultan ser los niveles de energía correctos, aparte de pequeñas correcciones que no se pueden explicar en este tratamiento pseudo-clásico. A pesar de que las energías son esencialmente correctas, el modelo Bohr enmascara la verdadera naturaleza cuántica del electrón, que solo emerge de un análisis mecánico completamente cuántico.
Calcule un valor para el radio de Bohr usando Ecuación\(\ref{1.8.16}\) para verificar que esta ecuación sea consistente con el valor 52.9 pm. ¿Para qué sería el radio\(n = 1\) en el\(\ce{Li^{2+}}\) ion?
- Contestar
-
Partiendo de la ecuación\ ref {1.8.16} y resolviendo para\(r\):
\[ \begin{align*} \dfrac{Ze^2m_er}{4πϵ_0} &=n^2ℏ^2 \\ r &=\dfrac{4 n^2 \hbar^2 πϵ_0}{Z e^2 m_e} \end{align*} \nonumber \]
con
- \(e\)es la carga fundamental:\(e=1.60217662 \times 10^{-19}C^2\)
- \(m_e\)es la masa de un electrón:\(m_e= 9.10938356 \times 10^{-31}kg\)
- \(\epsilon_o\)es la permitividad del espacio libre:\(\epsilon_o = 8.854 \times 10^{-12}C^2N^{-1}m^{-2}\)
- \(\hbar\)es la constante de tablones reducidos:\(\hbar=1.0546 \times 10^{-34}m^2kg/s\)
Para el estado fundamental del átomo de hidrógeno:\(Z=1\) y\(n=1\).
\[ \begin{align*} r &=\dfrac{4 \hbar^2 πϵ_0}{e^2m_e} \\ &= \dfrac{4 (1.0546 \times 10^{-34}m^2kg/s)^2 \times π \times 8.854 \times 10^{-12}C^2N^{-1}m^{-2}}{(1.60217662 \times 10^{-19}C)^2(9.10938356 \times 10^{-31}kg)} \\ &=5.29 \times 10^{-11}m = 52.9\, pm\end{align*} \nonumber \]
Para el estado fundamental del ion litio +2:\(Z=3\) y\(n=1\)
\[ \begin{align*} r &=\dfrac{4 \hbar^2 πϵ_0}{3 e^2m_e} \\ &= \dfrac{4 (1.0546 \times 10^{-34}m^2kg/s)^2 \times π \times 8.854\times10^{-12}C^2N^{-1}m^{-2}}{3(1.60217662 \times 10^{-19}C)^2(9.10938356 \times 10^{-31}kg)} \\ &=1.76 \times 10^{-11}m = 17.6 \,pm\end{align*} \nonumber \]
Como era de esperar, el\(\ce{Li^{2+}}\) tiene un radio menor que los\(\ce{H}\) átomos debido al aumento de la carga nuclear.
¿Cómo varían los radios de las órbitas de hidrógeno\(n\)? Preparar una gráfica que muestre\(r\) como una función de\(n\). Se\(n = 200\) han preparado estados de átomos de hidrógeno (llamados estados de Rydberg). ¿Cuál es el diámetro de los átomos en estos estados?
- Contestar
-
Esta es una aplicación sencilla de la Ecuación de\ ref {1.8.16B}. El átomo de hidrógeno solo tiene ciertos radios permisibles y estos radios se pueden predecir a partir de la ecuación que los relaciona con cada uno\(n\). Tenga en cuenta que el electrón debe estar en movimiento por lo que no\(n = 0\) está permitido.
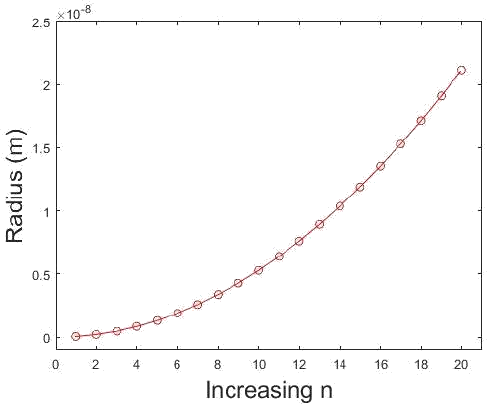
Esta gráfica muestra la relación de radio en función de\(n\). Tenga en cuenta que en\(n=1\) el radio no es cero. (CC BY-NC; Ümit Kaya vía LibreTexts) \(4 \pi \epsilon_{0}=1.113 \times 10^{-10} \mathrm{C}^{2} \mathrm{J}^{-1} \mathrm{m}^{-1}\)y\(\hbar=1.054 \times 10^{-34} \mathrm{J} \mathrm{s},\) también sabiendo
\ [\ begin {aligned}
e &=1.602\ times 10^ {-19}\ mathrm {C}\ text {con}\\
m_ {e} &=9.109\ times 10^ {-31}\ mathrm {kg}
\ end {alineado}\ nonumber\]y\(Z\) es la carga nuclear, utilizamos esta ecuación directamente. Se puede hacer una simplificación aprovechando el hecho de que
\[a_{0}=\frac{4 \pi \epsilon_{0} \hbar^{2}}{e^{2} m_{e}} \nonumber \]
resultando en
\[r_{n}=\frac{a_{0}}{Z} n^{2} \nonumber \]
donde\(a_{0}=5.292 \times 10^{-11} \mathrm{m}\) que es el Radio de Bohr.
Supongamos que queremos encontrar el radio donde\(n=200 . n^{2}=40000\) tan enchufando directamente tenemos
\[ \begin{align*} r_{n} &=\frac{\left(5.292 \times 10^{-11}\right)}{(1)}(40000) \\[4pt] &=2.117 \times 10^{-6} m \end{align*} \nonumber \]
para el radio de un átomo de hidrógeno con un electrón excitado al\(\mathrm{n}=200\) estado. El diámetro es entonces\(4.234 \times 10^{-6} \mathrm{m}\).
El argumento de la onda para la cuantificación
La discusión anterior se basa en una imagen clásica de un electrón en órbita con la cuantificación del requisito de momento angular (Ecuación\(\ref{1.8.15}\)) levantada de los argumentos de cuantificación de Planck. De ahí que solo permita que ciertas trayectorias sean estables (con radios diferentes). Sin embargo, como se discutió anteriormente, el electrón tendrá una propiedad de onda también con una longitud de onda de Broglie\(\lambda\)
\[\lambda = \dfrac{h}{p} \nonumber \]
Por lo tanto, un impulso mayor\(p\) implica una longitud de onda más corta. Eso significa que a medida que\(n\) aumenta (Ecuación\(\ref{1.8.21}\)), la longitud de onda también debe aumentar; esta es una característica común en la mecánica cuántica y a menudo se observará. En el átomo de Bohr, la simetría circular y la propiedad de onda del electrón requiere que las ondas electrónicas tengan un número entero de longitudes de onda (Figura\(\PageIndex{1A}\)). Si no, entonces las ondas se superpondrán imperfectamente y se cancelarán (es decir, el electrón dejará de existir) como se demuestra en la Figura\(\PageIndex{1B}\).
Una discusión más detallada sobre el efecto de las ondas electrónicas en los átomos se discutirá en los siguientes capítulos.
Derivación de la ecuación de Rydberg a partir del modelo de Bohr
Ante una predicción de las energías permitidas de un sistema, ¿cómo podríamos ir para verificarlas? La técnica experimental general conocida como espectroscopia nos permite sondear las diversas diferencias entre las energías permitidas. Así, si la predicción de las energías reales, en sí mismas, es correcta, también deberíamos ser capaces de predecir estas diferencias. Supongamos que somos capaces de colocar el electrón en el átomo de hidrógeno de Bohr en un estado energético\(E_n\) para\(n>1\), es decir, uno de sus llamados estados excitados. El electrón volverá rápidamente a su estado de energía más bajo, conocido como el estado fundamental y, al hacerlo, emitirá luz. La energía arrastrada por la luz viene determinada por la condición de que la energía total es conservada (Figura 1.8.6 ).
Así, si\(n_i\) es el entero el que caracteriza el estado inicial (excitado) del electrón, y\(n_f\) es el estado final (aquí lo imaginamos\(n_f =1\), pero es aplicable en casos que\(n_f <n_i\), es decir, emisión)
\[E_{nf}=E_{ni}-h\nu \label{1.8.22} \]
o
\[\nu=\dfrac{E_{ni}-E_{nf}}{h}=\dfrac{Z^2 e^4 m_e}{8\epsilon_{0}^{2} h^3}\left ( \dfrac{1}{n_{f}^{2}}-\dfrac{1}{n_{i}^{2}}\right ) \label{1.8.23} \]
Ahora podemos identificar la constante de Rydberg\(R_H\) con la relación de constantes en el lado derecho de la ecuación\(\ref{1.8.23}\)
\[ R_H = \dfrac {m_ee^4}{8 \epsilon ^2_0 h^3 } \label {2-22} \]
Evaluar\(R_H\) a partir de las constantes fundamentales en esta fórmula da un valor dentro del 0.5% del obtenido experimentalmente del espectro de átomos de hidrógeno.
Así, al observar la luz emitida, podemos determinar la diferencia de energía entre los niveles de energía inicial y final, lo que da como resultado los espectros de emisión discutidos en las Secciones 1.4 y 1.5. Diferentes valores de\(n_f\) determinan qué espectro de emisión se observa, y los ejemplos mostrados en la figura llevan el nombre de los individuos que los observaron por primera vez. La siguiente figura muestra algunas de las transiciones posibles para diferentes\(n_f\) y\(n_i\) valores discutidos anteriormente.
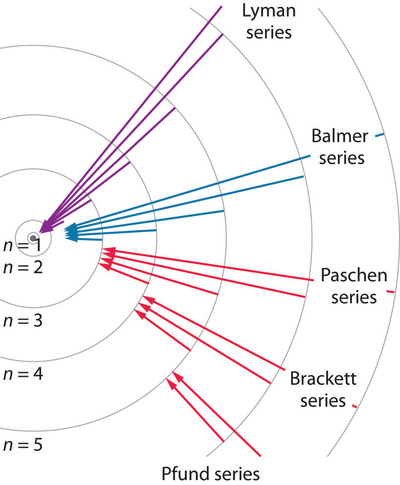
Si el átomo absorbe luz termina en un estado excitado como resultado de la absorción. La absorción sólo es posible para la luz de ciertas frecuencias, y nuevamente, la conservación de la energía determina cuáles son estas frecuencias. Si la luz es absorbida, entonces la energía final se\(E_{nf}\) relacionará con la energía inicial\(E_{ni}\) con\(n_f >n_i\)
\[E_{nf}=E_{ni}+h\nu \label{1.8.24} \]
o
\[\nu=\dfrac{E_{nf}-E_{ni}}{h}=\dfrac{Z^2 e^4 m_e}{8\epsilon_{0}^{2}h^3}\left ( \dfrac{1}{n_{i}^{2}}-\dfrac{1}{n_{f}^{2}}\right ) \label{1.8.25} \]
Ejercicio 1.8.3
- Calcular la energía de un fotón que se produce cuando un electrón en un átomo de hidrógeno va de una órbita con\(n = 4\) a una órbita con\(n = 1\).
- ¿Qué sucede con la energía del fotón a medida que el valor inicial de\(n\) se acerca al infinito?
- Contestar
-
a:
\ [\ begin {align*}
E_ {\ text {nf}} &= E_ {ni} - h\ nu\\
E_ {fotón} = h\ nu &= E_ {nf} - E_ {ni}\\
&=\ frac {z^2e^4m_E} {8\ epsilon_o^2h^2}\ izquierda (\ frac {1} n_f^2} -\ frac {1} {n_i^2}\ derecha)\\
&=\ frac {e^4m_e} {8\ epsilon_o^2h^2}\ izquierda (\ frac { 1} {1^2} -\ frac {1} {4^2}\ derecha)\\
&=2.18\ times 10^ {-18}\ left (1 -\ frac {1} {16}\ right)\\
&=2.04\ times 10^ {-18} J
\ end {align*}\ nonumber\]b:
Como\(n_i \rightarrow \infty\)
\ [\ begin {align*}
E_ {fotón} &=\ frac {e^4m_e} {8\ epsilon_o^2h^2}\ izquierda (\ frac {1} {n_f^2} -\ frac {1} {n_i^2}\ derecha)
\\ frac {1} {n_i^2} &\ fila derecha 0\\
E_ {fotón} &\ fila derecha\ frac {e^4m_e} {8\ epsilon_o^2h^2}\ izquierda (\ frac {1} {n_f^2}\ derecha)\\
\ end {align*}\ nonumber\]
La propuesta de Bohr explicó el espectro de átomos de hidrógeno, el origen de la fórmula de Rydberg y el valor de la constante de Rydberg. Específicamente demostró que los números enteros en la fórmula de Rydberg son una manifestación de cuantificación. La energía, el momento angular y el radio del electrón orbitante están cuantificados. Esta cuantificación también es paralela al concepto de órbitas estables en el modelo de Bohr. Solo ciertos valores de\(E\),\(M\), y\(r\) son posibles, y por lo tanto el electrón no puede colapsar sobre el núcleo irradiando continuamente energía porque solo puede tener ciertas energías, y no puede estar en ciertas regiones del espacio. El electrón sólo puede saltar de una órbita (estado cuántico) a otra. La cuantificación significa que las órbitas son estables y el electrón no puede entrar en espiral en el núcleo a pesar de la atractiva fuerza de Coulomb.
Aunque las ideas de Bohr explicaron con éxito el espectro de hidrógeno, fracasaron cuando se aplicaron a los espectros de otros átomos. Además quedó una pregunta profunda. ¿Por qué se cuantifica el momento angular en unidades de\(\hbar\)? Como veremos, de Broglie tuvo una respuesta a esta pregunta, y esta respuesta llevó a Schrödinger a un postulado general que produce la cuantificación del momento angular como consecuencia. Esta cuantificación no es tan simple como la propuesta por Bohr, y veremos que no es posible determinar la distancia del electrón desde el núcleo con tanta precisión como pensaba Bohr. De hecho, dado que la posición del electrón en el átomo de hidrógeno no está en absoluto tan bien definida como una órbita clásica (como la luna que orbita la tierra) se le llama orbital. Un electrón orbital representa o describe la posición del electrón alrededor del núcleo en términos de una función matemática llamada función de onda que produce la probabilidad de posiciones del electrón.
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski
- Template:Contriboundless

