8.7: Los cálculos de Hartree-Fock dan buena concordancia con los datos experimentales
- Page ID
- 79669
- Comprender cómo se expande el método Hartree para incluir funciones de onda determenciales de electrones mulitas simétricas a través de las ecuaciones de Hartree-Fock.
- Entender cómo calcular las energías orbitales a partir de la teoría de HF.
- Aplicar la teoría de HF con la teoría de Koopman para estimar las energías de ionización y afinidades electrónicas.
El método Hartree discutido anteriormente es útil como introducción a la solución del sistema de muchas partículas y a los conceptos de autoconsistencia y de los cálculos de campo autoconsistente, pero su importancia se limita a la historia de la física. De hecho el método de Hartree no es solo aproximado, es fundamentalmente erróneo ya que su función de onda no es antisimétrica a la permutación de electrones! El enfoque de Hartree-Fock que se analiza a continuación es un mejor enfoque, que toma en cuenta correctamente el carácter antisimétrico de las funciones de onda de prueba.
Aunque las ecuaciones de Hartree son manejables numéricamente a través del método de campo autoconsistente, no es sorprendente que una aproximación tan cruda no logre capturar elementos de la física esencial. El principio de exclusión de Pauli exige que la función de onda de muchos cuerpos sea antisimétrica con respecto al intercambio de cualesquiera dos coordenadas electrónicas, p.
\[\Psi(\mathbf{r}_{1},\mathbf{r}_{2}, \ldots, \mathbf{r}_{N}) = - \Psi(\mathbf{r}_{2},\mathbf{r}_{1}, \ldots, \mathbf{r}_{N}) \label{2.7} \]
que claramente no pueden ser satisfechas por las funciones de onda multi-electrón de la forma utilizada en la Aproximación de Hartree, es decir, la aproximación orbital (Ecuación\(\ref{2.3}\)).
\[\Psi(\mathbf{r}_1,\mathbf{r}_2, \ldots, \mathbf{r}_N) \approx \psi_{1}(\mathbf{r}_1)\psi_{2}(\mathbf{r}_2) \ldots \psi_{N}(\mathbf{r}_N) \label{2.3} \]
Esta condición de indistinguibilidad puede satisfacerse formando un determinante Slater de orbitales de una sola partícula
\[\Psi(\mathbf{r}_{1}, \mathbf{r}_{2}, \ldots, \mathbf{r}_{N})= \dfrac{1}{\sqrt{N}} \left \vert\psi(\mathbf{r}_{1})\psi(\mathbf{r}_{2}) \ldots \psi(\mathbf{r}_{N}) \right\vert \label{2.8} \]
Esto desacopla los electrones dando como resultado ecuaciones de Hartree-Fock de\(N\) una sola partícula:
\[\underbrace{-\dfrac{\hbar^{2}}{2m}\nabla^{2}\psi_{i}(\mathbf{r})}_{\text{kinetic energy}} + \underbrace{V_{nucleus}(\mathbf{r})\psi_{i}(\mathbf{r})}_{\text{electron-nucleus potential}} + \underbrace{V_{electron}(\mathbf{r})\psi_{i}(\mathbf{r})}_{\text{Hartree Term}} - \sum_{j} \int d\mathbf{r}^{\prime} \dfrac{\psi^{\star}_{j}(\mathbf{r}') \psi^{\star}_{i}(\mathbf{r}') \psi_{j}(\mathbf{r}) } {\left \vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} = \epsilon_{i}\psi_{i}(\mathbf{r}). \label{2.9} \]
Al igual que con las ecuaciones de Hartree, el primer término es la energía cinética del\(i^{th}\) electrón
\[-\dfrac{\hbar^{2}}{2m}\nabla^{2}\psi_{i}(\mathbf{r}) \nonumber \]
y el segundo término es el potencial electrón-núcleo entre el\(i^{th}\) electrón y el núcleo
\[V_{nucleus}(\mathbf{r})\psi_{i}(\mathbf{r}) \nonumber \]
El tercer término (a veces llamado término “Hartree”) es el potencial electrostático entre el\(i^{th}\) electrón y la distribución de carga promedio de los otros electrones N-1.
\[V_{electron}(\mathbf{r})\psi_{i}(\mathbf{r}) = J_{j,k} = \int |\phi_j(r)|^2 |\phi_k(r’)|^2 \dfrac{e^2}{r-r'} dr dr’ \label{8.3.9} \]
Estos tres términos son idénticos a las ecuaciones de Hartree con el producto wavefunction ansatz (es decir, aproximación orbital). El cuarto término de la Ecuación no\(\ref{2.9}\) está en las Ecuaciones de Hartree:
\[\sum_{j} \int d\mathbf{r}^{\prime} \dfrac{\psi^{\star}_{j}(\mathbf{r}') \psi^{\star}_{i}(\mathbf{r}') \psi_{j}(\mathbf{r}) } {\left \vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} \nonumber \]
y es el término de intercambio. Este término se asemeja al término directo de Coulomb, pero para los índices intercambiados. Es una manifestación del principio de exclusión Pauli, y actúa para separar electrones del mismo giro. Este término de “intercambio” actúa únicamente sobre electrones con el mismo giro y proviene de la forma determinante de Slater de la función de onda. Físicamente, el efecto del intercambio es que los electrones de espín similar se eviten entre sí. El término de intercambio se suma considerablemente a la complejidad de estas ecuaciones.
Las ecuaciones de Hartree-Fock en la ecuación se\(\ref{2.9}\) pueden refundir como una serie de ecuaciones similares a Schrödinger:
\[ \hat {F} | \varphi _i \rangle = \epsilon _i| \varphi _i \rangle \label {8.7.2} \]
donde\(\hat {F}\) se llama el operador Fock y\( \{| \varphi_i \rangle \}\) son los orbitales Hatree-Fock con las energías correspondientes\(\epsilon_i\).
El operador Fock es un operador de un electrón y resolver una ecuación de Hartree-Fock da la energía y el orbital Hartree-Fock para un electrón. Para un sistema con 2N electrones, la variable i variará de 1 a N; es decir, habrá una ecuación para cada orbital. La razón de esto es que solo se utilizan las funciones de onda espaciales en la Ecuación\(\ref{8.7.2}\). Dado que la porción espacial de un orbital puede usarse para describir dos electrones, cada una de las energías y funciones de onda encontradas al resolver Ecuación se\(\ref{8.7.2}\) utilizará para describir dos electrones.
La naturaleza del operador Fock revela cómo el método Hartree-Fock (HF) o Campo Self-Consistente (SCF) explica la interacción electrón-electrón en átomos y moléculas mientras preserva la idea de orbitales atómicos independientes. La función de onda escrita como determinante de Slater de los orbitales giratorios es necesaria para derivar la forma del operador Fock, que es
\[\hat {F} = \hat {H} ^0 + \sum _{j=1}^N ( 2 \hat {J} _j - \hat {K} _j ) = -\dfrac {\hbar ^2}{2m} \nabla ^2 - \dfrac {Ze^2}{4 \pi \epsilon _0 r} + \sum _{j=1}^N (2\hat {J}_j - \hat {K} _j ) \label {8.7.3} \]
Como lo demuestra la versión expandida en el extremo derecho, el primer término en esta ecuación,\(\hat {H}^0\), es el familiar operador similar al hidrógeno que da cuenta de la energía cinética de un electrón y la energía potencial de este electrón interactuando con el núcleo. El siguiente término da cuenta de la energía potencial de un electrón en un campo promedio creado por todos los demás electrones en el sistema. \(\hat {K}\)Los operadores\(\hat {J}\) y resultan de los términos de repulsión electrón-electrón en el Hamiltoniano completo para un sistema multi-electrón. Estos operadores involucran los orbitales de un electrón así como la energía de interacción electrón-electrón.
El operador Fock (Ecuación\(\ref{8.7.3}\)) depende de todos los orbitales ocupados (debido a los operadores de intercambio y Coulomb). Por lo tanto, un orbital específico sólo se puede determinar si todos los demás son conocidos. Se deben usar métodos iterativos para resolver las ecuaciones de HF como el método de campo autoconsistente discutido anteriormente para la Aproximación de Hartree.
La interacción de intercambio es un efecto mecánico cuántico que solo ocurre entre partículas idénticas. A pesar de que a veces se le llama una fuerza de intercambio en analogía con la fuerza clásica, no es una verdadera fuerza, ya que carece de un portador de fuerza. El efecto se debe a que la función de onda de partículas indistinguibles están sujetas a simetría de intercambio, es decir, permaneciendo inalteradas (simétricas) o cambiando su signo (antisimétrico) cuando se intercambian dos partículas. Tanto los bosones como los fermiones pueden experimentar la interacción de intercambio. Para los fermiones, a veces se le llama repulsión de Pauli y se relaciona con el principio de exclusión de Pauli. Para los bosones, la interacción de intercambio toma la forma de una atracción efectiva que hace que las partículas idénticas se encuentren más juntas, como en la condensación Bose-Einstein.
Por ejemplo, el electrón 1 en helio (con\(Z=2\)), luego
\[\hat {H}^0 (1) = - \dfrac {\hbar ^2}{2m} \nabla ^2_1 - \dfrac {2e^2}{4 \pi \epsilon _0 r_1} \label {8.7.4} \]
El operador Fock se expresa en términos de las coordenadas de un electrón cuya perspectiva estamos tomando (que llamaremos electrón 1 a lo largo de la siguiente discusión), y el campo promedio creado por todos los demás electrones en el sistema se construye en términos de las coordenadas de un genérico” otro electrón” (que llamaremos electrón 2) que se considera que ocupa cada orbital a su vez durante la suma sobre los N orbitales espaciales.
Al igual que con las ecuaciones de Hartree, resolver las ecuaciones de Hartree-Fock es matemáticamente equivalente a asumir que cada electrón interactúa solo con la nube de carga promedio de los otros electrones. Es así como se maneja la repulsión electrón-electrón. Esto también es por lo que a este enfoque se le llama también el enfoque de Campo Autoconsistante (SCF).
Las mejores funciones de onda de un electrón posibles, por definición, darán la energía total más baja posible para un sistema multielectrónico utilizado con el multielectrón completo Hamiltoniano para calcular el valor de expectativa para la energía total del sistema. Estas funciones de onda se llaman las funciones de onda Hartree-Fock y la energía total calculada es la energía Hartree-Fock del sistema.
Hartree-Fock Energía
Las ecuaciones de Hartree-Fock\(h_e \phi_i = \epsilon_i \phi_i\) implican que las energías orbitales\(\epsilon_i\) pueden escribirse como:
\[ \begin{align*} \epsilon_i &= \langle \phi_i | h_e | \phi_i \rangle \\[4pt] &= \langle \phi_i | T + V | \phi_i \rangle + \sum_{j({\rm occupied})} \langle \phi_i | J_j - K_j | \phi_i \rangle \label{8.7.6} \\[4pt] &= \langle \phi_i | T + V | \phi_i \rangle + \sum_{j({\rm occupied})} [ J_{i,j} - K_{i,j} ],\label{8.7.7} \end{align*} \]
donde\(T + V\) representa las energías cinética (\(T\)) y de atracción nuclear (\(V\)), respectivamente. Así,\(\epsilon_i\) es el valor promedio de la energía cinética más la atracción coulómbica a los núcleos para un electrón in\(\phi_i\) más la suma sobre todos los espín-orbitales ocupados en\(\psi\) de Coulomb menos Interacciones de intercambio de estos electrones con el electrón adentro\(\phi_i\).
Si\(\phi_i\) es un spin-orbital ocupado, el\(j = i\) término\([ J_{i,i} - K_{i,i}]\) desaparece en la suma anterior y los términos restantes en la suma representan la interacción de Coulomb menos intercambio de\(\phi_i\) con todos los\(N-1\) demás orbitales espín-orbitales ocupados. Si\(\phi_i\) es un spin-orbital virtual, esta cancelación no ocurre porque la suma sobre\(j\) no incluye\(j = i\). Entonces, se obtiene la interacción de intercambio de Coulomb menos\(\phi_i\) con todos\(N\) los orbitales spin-orbitales ocupados en\(\psi\). De ahí que las energías de los orbitales ocupados pertenecen a interacciones apropiadas a un total de\(N\) electrones, mientras que las energías de los orbitales virtuales pertenecen a un sistema con\(N+1\) electrones. Esta diferencia es muy importante de entender y de tener en cuenta.
Para dar una idea de lo bien que la teoría de HF puede predecir las energías de estado fundamental de varios átomos, considere la Tabla 8.7.1 a continuación:
| Atom | Hartree-Fock Energía | Experimento |
|---|---|---|
| \(He\) | \(-5.72\) | \(-5.80\) |
| \(Li\) | \(-14.86\) | \(-14.96\) |
| \(Ne\) | \(-257.10\) | \(-257.88\) |
| \(Ar\) | \(-1053.64\) | \(-1055.20\) |
Teorema de Koopman
El teorema de Koopman afirma que la primera energía de ionización es igual a la negativa de la energía orbital del orbital molecular ocupado más alto. De ahí que la energía de ionización requerida para generar un catión y un electrón separado se representa por la eliminación de un electrón de un orbital sin cambiar las funciones de onda de los otros electrones. A esto se le llama la “aproximación orbital congelada”. Consideremos el siguiente modelo del desprendimiento o unión de un electrón en un sistema\(N\) -electrón.
- En este modelo, tanto la molécula parental como las especies generadas por la adición o eliminación de un electrón se tratan a nivel de determinante único.
- Los orbitales Hartree-Fock de la molécula parental se utilizan para describir ambas especies. Se dice que dicho modelo descuida la relajación orbital (es decir, la reoptimización de los orbitales espín para permitirles llegar a ser apropiados a la especie hija).
Dentro de este modelo, la diferencia de energía entre el hijo y el padre se puede escribir de la siguiente manera (\(\phi_k\)representa el spin-orbital particular que se agrega o elimina:
- para desprendimiento de electrones (energías de ionización vertical)\[ \color{red} E_{N-1} - E_N = - \epsilon_k \label{8.7.8} \]
- y para la unión de electrones (afinidades de electrones)\[ \color{red} E_N - E_{N+1} = - \epsilon_k .\label{8.7.9} \]
Derivamos este resultado para el caso en el que se agrega un electrón al\(N+1^{st}\) spin-orbital. La energía del determinante\(N\) -electrón con espín-orbitales\(\phi_1\) a través de\(f_N\) ocupado es
\[E_N = \sum_{i=1}^N \langle \phi_i | T + V | \phi_i \rangle + \sum_{i=1}^{N} [ J_{i,j} - K_{i,j} ] \nonumber \]
que también se puede escribir como
\[E_N = \sum_{i=1}^N \langle \phi_i | T + V | \phi_i \rangle + \frac{1}{2} \sum_{i,j=1}^{N} [ J_{i,j} - K_{i,j} ].\nonumber \]
Asimismo, la energía\(N+1\) de la función de onda determinante de electrones es
\[E_{N+1} = \sum_{i=1}^{N+1} \langle \phi_i | T + V | \phi_i \rangle + \frac{1}{2} \sum_{i,j=1}^{N+1} [ J_{i,j} - K_{i,j} ]. \nonumber \]
La diferencia entre estas dos energías viene dada por
\[ \begin{align*} E_{N} – E_{N+1} = &- \langle \phi_{N+1} | T + V | \phi_{N+1} \rangle - \frac{1}{2} \sum_{i=1}^{N+1} [ J_{i,N+1} - K_{i,N+1} ] \\[4pt] &- \frac{1}{2} \sum_{j=1}^{N+1} [ J_{N+1,j} - K_{N+1,j} ] \\[4pt] &= - \langle \phi_{N+1} | T + V | \phi_{N+1} \rangle - \sum_{i=1}^{N+1} [ J_{i,N+1} - K_{i,N+1} ] \\[4pt] &= - \epsilon_{N+1}. \end{align*} \nonumber \]
Es decir, la diferencia de energía es igual a menos la expresión para la energía del\(N+1^{st}\) spin-orbital, que se dio antes.
Las ecuaciones de Hartree-Fock tratan exactamente el intercambio; sin embargo, las ecuaciones descuidan correlaciones más detalladas debido a interacciones de muchos cuerpos. Los efectos de las correlaciones electrónicas no son despreciables; de hecho, el fracaso de la teoría de Hartree-Fock para incorporar con éxito la correlación conduce a uno de sus fracasos más celebrados.
En la Interpretación de Copenhague, el módulo cuadrado de la función ondulada da la probabilidad de encontrar una partícula en un lugar dado. La función de onda de muchos cuerpos da la función de distribución de partículas N,\(|Φ(r_1, ..., r_N )|^2\) es decir, es la densidad de probabilidad de que la partícula 1 esté en\(r_1\),..., y la partícula\(N\) está en\(r_N\). Sin embargo, al tratar de calcular la interacción entre electrones, lo que queremos saber es la probabilidad de encontrar un electrón en\(r\), dadas las posiciones de todos los demás electrones\(\{r_i\}\). Esto implica que el electrón se comporta mecánicamente cuántico cuando evaluamos su función de onda, pero como una partícula puntual clásica cuando contribuye al potencial visto por los otros electrones.
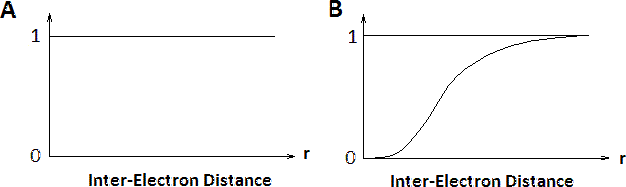
Las contribuciones de las interacciones electrón-electrón en sistemas de electrones N dentro de los métodos Hartree y Hartree-Fock se muestran en la Figura 8.7.2 . Las distribuciones de probabilidad electrónica condicional\(n(r)\) de\(N-1\) electrones alrededor de un electrón con espín dado situado en\(r=0\). Dentro de la aproximación de Hartree, todos los electrones son tratados como independientes, por lo tanto\(n(r)\) es sin estructura. Sin embargo, dentro de la aproximación Hartree-Fock, la función de onda\(N\) -electrón refleja el principio de exclusión de Pauli y cerca del electrón en\(r=0\) el agujero de intercambio se puede ver donde se reduce la densidad de espines igual a la del electrón central. Los electrones con espines opuestos no se ven afectados (no se muestran).
Resumen
Entonces, dentro de las limitaciones del HF, modelo orbital congelado, los potenciales de ionización (IPs) y las afinidades electrónicas (EA) se dan como el negativo de las energías spin-orbitales ocupadas y virtuales, respectivamente. Esta afirmación se conoce como el teorema de Koopman; se usa ampliamente en cálculos químicos cuánticos como medio para estimar potenciales de ionización (Ecuación\(\ref{8.7.8}\)) y Afinidades Electrónicos (Ecuación\(\ref{8.7.9}\)) y a menudo produce resultados que son cualitativamente correctos (es decir, ± 0.5 eV). En general, la teoría de Hartree-Fock da una gran solución de primer orden (99%) a la descripción de sistemas multi-electrón, pero ese último 1% sigue siendo demasiado grande para describir cuantitativamente muchos aspectos de la química y son necesarios enfoques más sofisticados. Éstos se discuten en otra parte.
Colaboradores y Atribuciones
- Template:ContribAukland
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

