10.1: Los orbitales híbridos tienen en cuenta la forma molecular

Objetivos de aprendizaje

• Introducir orbital híbrido para explicar la estructura molecular no lineal

La teoría del enlace de valencia (VB) es una de las dos teorías básicas, junto con la teoría orbital molecular (MO), que se desarrollaron para utilizar los métodos de la mecánica cuántica para explicar la unión química. Se centra en cómo se combinan los orbitales atómicos de los átomos disociados para dar enlaces químicos individuales cuando se forma una molécula. En contraste, la teoría orbital molecular, que se discutirá en otra parte, predicen las funciones de onda que cubren toda la molécula.

Revisión de Diatómica

Consideremos\(H_2\). Recordemos que la estructura de Lewis para un solo\(H\) átomo es\(H\cdot\) y para\(H_2\), lo es\(H:H\). Así, cada hidrógeno trae un electrón desapareado al enlace. Que los dos protones se denoten A y B y los dos electrones 1 y 2. Ahora, considere la energía potencial

\[\begin{align} V &= V_{ee}+V_{en}+V_{nn}\\[4pt] &=\dfrac{e^2}{4\pi \epsilon_0}\left [ \dfrac{1}{r_{12}}-\dfrac{1}{r_{1A}}-\dfrac{1}{r_{1B}}-\dfrac{1}{r_{2A}}-\dfrac{1}{r_{2B}}+\dfrac{1}{R_{AB}}\right ] \end{align} \nonumber \]

Pero a medida\(R_{AB}\rightarrow \infty\) que los\(1/R_{AB}\) términos\(1/r_{12}\) \(1/r_{1B}\),\(1/r_{2A}\),, y desaparecen y la energía potencial se convierte simplemente en la de dos átomos de hidrógeno que no interactúan

\[V\rightarrow -\dfrac{e^2}{4\pi \epsilon_0}\left [ \dfrac{1}{r_{1A}}+\dfrac{1}{r_{2B}}\right ] \nonumber \]

Dado que la energía potencial se convierte en una simple suma de energías separadas para los electrones 1 y 2, la función de onda debería ser simplemente un producto\(\psi_{1s}(r_1 -r_A)\psi_{1s}(r_2 -r_B)\). Pero como dejamos\(R_{AB}\rightarrow R_e\), dónde\(R_e\) está la longitud del enlace de equilibrio, los electrones se mezclan, y ya no podemos decir si el electrón 1 pertenece al átomo A o al átomo B y lo mismo para el electrón 2. Por lo tanto, necesitamos construir una combinación de productos que sea consistente con el principio de exclusión de Pauli. Si solo consideramos las coordenadas\(r_1\) y\(r_2\) de los electrones, entonces la única función de onda que podemos construir a partir de un producto de 1s orbitales es

\[\psi_u (r_1 ,r_2)=C_u [\psi_{1s}^{A}(r_1)\psi_{1s}^{B} (r_2)-\psi_{1s}^{A}(r_2)\psi_{1s}^{B}(r_1)] \nonumber \]

donde el\(u\) designator indicates that this is an odd function. The constant \(C_u\) es la constante de noramlización general. Desafortunadamente, como en el método LCAO, tal función de onda es antiadhesión y no es una buena representación del estado fundamental. Si, sin embargo, construimos la función de onda

\[\psi_g (r_1 ,r_2)=C_g [\psi_{1s}^{A} (r_1)\psi_{1s}^{B} (r_2)+\psi_{1s}^{A}(r_2) \psi_{1s}^{B} (r_1)] \nonumber \]

(donde\(g\) designates that this is an even function), we violate the Pauli exclusion principle, even though such a wavefunction leads to a stable chemical bond.

Lo que falta aquí es el hecho de que no hemos considerado los giros de los electrones. Dado que los electrones son idénticos, si intercambiamos coordenadas y giros, entonces la función de onda debería cambiar de signo. Por lo tanto, podemos hacer que ambas funciones de onda anteriores sean consistentes con el principio de exclusión de Pauli multiplicando por una función de onda de giro apropiada. Obtenemos

\[\begin{align}\psi_u (r_1 ,r_2 ,s_1 ,s_2 ) &=\psi_u(x_1 ,x_2)=C_u [\psi_{1s}^{A}(r_1)\psi_{1s}^{B}(r_2)-\psi_{1s}^{A}(r_2)\psi_{1s}^{B}(r_1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)+\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)]\\[4pt] \psi_g (r_1 ,r_2 ,s_1 ,s_2) &= \psi_g(x_1 ,x_2)=C_g[\psi_{1s}^{A}(r_1)\psi_{1s}{B}(r_2)+\psi_{1s}^{A}(r_2)\psi_{1s}^{B}(r_1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)]\end{align} \nonumber \]

donde\(s_1\) y\(s_2\) son los componentes z de spin para los electrones 1 y 2, respectivamente. Ahora podemos usar\(\psi_g\) como una función de onda aproximada de 2 electrones que conduce a un enlace químico estable en\(H_2\).

El hecho de que\(\psi_u\) es antienlace se puede determinar fácilmente buscando un plano nodal entre los dos átomos, en este caso, en el plano que biseca exactamente la línea que une los dos átomos, a medio camino entre ellos. Que esto es, efectivamente, un plano nodal se puede ver considerando dos puntos\(r_1\) y\(r_2\) para que los dos electrones que se toman se encuentren en este plano. Por simetría, las funciones\(\psi_{1s}^{A}(r_1)\) y\(\psi_{1s}^{B}(r_1)\) tienen el mismo valor para\(r_1\) en este plano, y lo mismo para\(\psi_{1s}^{B}(r_2)\) y\(\psi_{1s}^{A}(r_2)\). Asignemos los siguientes valores:

\[\begin{align}\psi_{1s}^{A}(r_1) &= \psi_{1s}^{B}(r_1)=A\\[4pt] \psi_{1s}^{B}(r_2) &= \psi_{1s}^{A}(r_2)=A' \end{align} \nonumber \]

Sustituyendo estos en\(\psi_u (x_1 ,x_2)\), obtenemos

\[\psi_u (x_1 ,x_2)=C_u [AA' -A' A][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)+\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)]=0 \nonumber \]

Dado que la función de onda tiene un nodo a medio camino entre los dos átomos, es claramente antienlace y debe tener una energía más alta que la función de onda de enlace correspondiente\(\psi_g\).

Un argumento similar puede ser usado para la molécula\(F_2\). Cada uno\(F\) tiene una configuración electrónica

\[1s^2 2s^2 2p_{x}^{2}2p_{y}^{2}2p_{z}^{1} \nonumber \]

y la estructura de Lewis de\(F_2\) es

Figura 10.1.1 : Estructura de Lewis de\(F_2\).

La mayoría de los electrones están en pares solitarios, pero los\(2p_z\) electrones, que están desapareados en cada\(F\) come together to form the bond. Thus, the bonding wavefunction should be a 2-electron wavefunction constructed from \(2p_z\) orbitales. La función de onda de unión toma la forma “gerade” como en\(H_2\):

\[\psi_g (r_1 ,r_2 ,s_1 ,s_2)=C_g [\psi_{2p_z}^{A}(r_1)\psi_{2p_z}^{B}(r_2)+\psi_{2p_z}^{A}(r_2)\psi_{2p_z}^{B}(r_1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)] \nonumber \]

Para\(HF\), the \(2p_z\) orbital encendido\(F\) and \(1s\) orbital on \(H\) come together to form the bonding wavefunction. To be consistent with the Pauli principle, we need a wavefunction of the form

\[\psi (r_1 ,r_2 ,s_1 ,s_2)=[\psi_{1s}^{H}(1)\psi_{2p_z}^{F}(2)+\psi_{1s}^{H}(2)\psi_{2p_z}^{F}(1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)] \label{1}) \]

Mirando los\(HF\) example, it becomes clear how much valence bond theory attempts to appear as a "quantum version'' of the Lewis dot structure model. Valence bond theory attempts to construct very approximate wavefunctions for the bonding electrons in a Lewis structure, leaving the orbitals unused in the construction of the valence bond wavefunctions for the lone pair electrons. In the case of \(HF\), we use the \(2p_z\) orbitales de\(F\), which leaves the \(2s\),\(2p_x\) y\(2p_y\) orbitales no utilizados. Dado que hay tres pares solitarios, estos tres orbitales son suficientes para mantener a cada una de las parejas solitarias como parejas spin-up/spin-down.

Hibridación

Para las moléculas poliatómicas, la teoría del enlace de valencia se convierte en una aproximación muy pobre porque las direccionalidades de los\(2p\) orbitales\(2s\) y son demasiado restrictivas para describir moléculas con números estéricos que oscilan entre 2 y 4. ¡El ejemplo considerado anteriormente\(H_2 O\) ilustra esto bastante dramáticamente! Consideremos una molécula aún más simple,\(BeH_2\), que tiene un número estérico de 2 y es lineal. Deje que los átomos se encuentren completamente a lo largo del eje z en la disposición\(H-Be-H\).

Aunque\(Be\) tiene una configuración electrónica de estado fundamental de\(1s^2 2s^2\), pero si “promovemos” uno de los\(2s\) electrones a un estado con mayor energía y permitimos que su estructura electrónica sea\(1s^2 2s 2p_z\), entonces los electrones desapareados en los\(2p_z\) orbitales\(2s\) y pueden combinarse con el electrones desapareados en cada uno de los átomos de hidrógeno para formar enlaces. La energía necesaria para excitar el electrón en Be sería ``reembolsada” por la energía ganada en la formación de enlaces estables. Las dos funciones de onda de enlace de valencia que construiríamos serían

\[\begin{align}\psi_1 (1,2) &= C_1 \left[\psi_{1s}^{H_1}(1)\psi_{2s}^{Be}(2)+\psi_{1s}^{H_1}(2)\psi_{2s}^{Be}(1) \right] \left[\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)\right]\\[4pt] \psi_2 (1,2) &= C_2 \left[\psi_{1s}^{H_2}(1)\psi_{2p_z}^{Be}(2)+\psi_{1s}^{H_2}(2)\psi_{2p_z}^{Be}(1)\right] \left[\psi_\uparrow (s_1)\psi_\downarrow (s_2)-\psi_\uparrow (s_2)\psi_\downarrow (s_1) \right]\end{align} \nonumber \]

Desafortunadamente, incluso este esquema simple no funciona del todo porque las dos\(Be-H\) bonds would be different due to their construction from different combinations of orbitals. By symmetry, however, we can see that the two \(BeH\) bonds should be equivalent. A solution to this problem was proposed by Linus Pauling in the 30s in the form of hibridaciones orbitales, un esquema que todavía usamos hoy en día.

Pauling utilizó el hecho de que en los períodos primero y segundo, los\(2p\) orbitales\(2s\) y tienen energías similares. En efecto, pues\(H\), las energías son exactamente las mismas. Dado que estas energías no son tan diferentes, podemos combinar orbitales s y p y aún así tener una solución válida de la ecuación de Schrödinger. Es decir, un orbital general

\[\chi (r)=C_1 \psi_{2s}(r)+C_2 \psi_{2p_x}(r)+C_3 \psi_{2p_y}(r)+C_4 \psi_{2p_z}(r) \nonumber \]

es también una solución de la ecuación de Schrödinger con la misma energía que a\(2s\) or \(2p\) orbitals individually (this is exactly true for \(H\)). In the case of \(BeH_2\), el potencial externo sobre los electrones en Be by the two hydrogens cambia los niveles de energía y crea una degeneración cercana entre los\(2s\) y\(2p_z\) orbitales, por lo tanto, ahora somos libres de combinar el en combinaciones lineales que son más adecuadas para la construcción tanto de las funciones de onda de enlace de valencia como de los MO a través del procedimiento LCAO.

\(sp\)Orbitales Híbridos

Para Be, ahora permitimos que los orbitales s y p se mezclen y creen dos orbitales híbridos conocidos como\(sp\) orbitales. Las dos nuevas funciones de onda híbridas como combinación lineal de las funciones para 2s y 2p _z (usando Dirac Notation):

\[| \chi_i \rangle = a_1|2s \rangle + b_1 |2p_z \rangle \label{sp1} \]

\[| \chi_j \rangle = a_2|2s \rangle + b_2 |2p_z \rangle \label{sp2} \]

Estas dos funciones de onda deben ser ortogonales.

\[ \langle \chi_i | \chi_j \rangle = \delta_{ij} \nonumber \]

Que se pueden separar en las siguientes relaciones:

\[ \langle \chi_i | \chi_i \rangle = 1 \label{norm1} \]

y

\[\langle \chi_j | \chi_j \rangle = 1 \label{norm2} \]

y

\[ \langle \chi_i | \chi_j \rangle = \langle \chi_j | \chi_i \rangle = 0 \label{ortho} \]

Las ecuaciones\(\ref{norm1}\) y\(\ref{norm2}\) son el requisito de normalidad y la ecuación\(\ref{ortho}\) es el requisito de ortogonalidad para las nuevas funciones de onda híbridas. Sustituir\(\ref{sp1}\) en\(\ref{norm1}\) resultados en

\[ \langle \chi_i | \chi_i \rangle = a_1^2 \cancelto{1}{\langle 2s | 2s \rangle } + a_1 b_1 \cancelto{0} {\langle 2s | 2p_z \rangle} + a_1 b_1 \cancelto{0} {\langle 2p_z | 2s} \rangle + b_1^2 \cancelto{1} {\langle 2p_z | 2p_z \rangle} =1 \nonumber \]

y de manera similar para\(\langle \chi_j | \chi_j \rangle\)

\[ \langle \chi_j | \chi_j \rangle = a_2^2 \cancelto{1}{\langle 2s | 2s \rangle } + a_2 b_2 \cancelto{0} {\langle 2s | 2p_z \rangle} + a_2 b_2 \cancelto{0} {\langle 2p_z | 2s} \rangle + b_2^2 \cancelto{1} {\langle 2p_z | 2p_z \rangle} =1 \nonumber \]

da como resultado las siguientes relaciones

\[ \langle \chi_i | \chi_i \rangle = a_1^2 + b_1^2 = 1 \label{Con1} \]

\[ \langle \chi_j | \chi_j \rangle = a_2^2 + b_2^2 = 1 \label{Con2} \]

y

\[ \langle \chi_i | \chi_j \rangle = a_1a_2 + b_1b_2 = 0 \label{Con3} \]

Se trata de cuatro incógnitas y tres ecuaciones. La cuarta “restricción” es que suponemos que la contribución de\(|s\rangle\) es la misma para ambos orbitales híbridos.

\[ a_1 = a_2 \nonumber \]

Ecuaciones\(\ref{Con1}\) a las que\(\ref{Con3}\) volver

\[a_1^2 + b_1^2 = 1 \label{Con1a} \]

\[ a_1^2 + b_2^2 = 1 \label{Con2a} \]

\[ b_1^2 = b_2^2 \label{Con3a} \]

Por lo tanto

\[ b_1 = -b_2 \nonumber \]

y

\[a_1 = b_1 \label{eq231} \]

Insertar Ecuación\ RefPEQ231} en\(\ref{Con3a}\) para obtener

\[a_1= \dfrac{1}{\sqrt{2}} \nonumber \]

y los dos orbitales híbridos son

\[\begin{align}\chi_1 (r) &= \dfrac{1}{\sqrt{2}}[\psi_{2s}(r)+\psi_{2p_z}(r)]\\[4pt] \chi_2 (r) &= \dfrac{1}{\sqrt{2}}[\psi_{2s}(r)-\psi_{2p_z}(r)]\end{align} \nonumber \]

Tenga en cuenta que estos orbitales son normalizados y ortogonales:

\[\int |\chi_1 (r)|^2 dV=1 \ ; \ \int |\chi_2 (r)|^2 dV=1 \ ; \ \int \chi_{1}^{*}(r)\chi_2 (r)dV=0 \nonumber \]

Estos orbitales aparecen como se muestra en la Figura 10.1.3

Figura 10.1.3 : La formación de orbitales híbridos sp. Tomando la suma y diferencia de un orbital atómico ns y un np donde n = 2 da dos orbitales híbridos sp equivalentes orientados a 180° entre sí.

Dado que los dos\(sp\) hybrid orbitals are mirror images of each other, they can overlap with the \(1s\) orbital of \(H\) (shown in the figure) and create two equal bonds, as needed for \(BeH_2\). Usando la formulación de enlace de valencia, ahora, uno de los\(BeH\) bonds will be described by a wavefunction of the form:

\[\begin{align}\psi_1 (1,2) &= C_1 [\psi_{1s}^{H_1}(1)\chi_{1}^{Be}(2)+\psi_{1s}^{H_1}(2)\chi_{1}^{Be}(1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)]\\[4pt] \psi_2 (1,2) &= C_2 [\psi_{1s}^{H_2}(1)\chi_{2}^{Be}(2)+\psi_{1s}^{H_2}(2)\chi_{2}^{Be}(1)][\psi_{\uparrow}(s_1)\psi_\downarrow (s_2)-\psi_{\uparrow}(s_2)\psi_\downarrow (s_1)]\end{align} \nonumber \]

En las anteriores funciones de onda, es evidente que\(H_1\) está a la derecha y\(H_2\) está a la izquierda, con base en las direccionalidades de\(\chi_1\) y\(\chi_2\).

\(sp^2\)Orbitales Híbridos

Para las moléculas planas trigonales como\(BH_3\), comenzamos con la configuración electrónica de\(B\), que es\(1s^2 2s^2 2p_x\), y promovemos uno de\(2s\) los electrones a un\(2p_y\) orbital, para que tengamos\(1s^2 2s 2p_x 2p_y\). Supongamos que la geometría de\(BH_3\) es tal que uno de los hidrógenos se encuentra a lo largo del eje x positivo. Los hidrógenos restantes estarían en los cuadrantes 3º y 4º, respectivamente, como se muestra en la Figura 10.1.4 .

Figura 10.1.4 : Geometría de\(BH_3\).

Si simplemente combinamos el\(2s\) con los\(2p_y\) orbitales\(2p_x\) y del boro, los orbitales híbridos resultantes no apuntarán en la dirección correcta. Por esta razón, crearemos versiones rotadas de los\(p_x\) y\(p_y\) orbitales, que, como veremos, equivalen a tomar nuevas combinaciones de\(2p_x\) y\(2p_y\) orbitales para combinar con el\(2s\). Dado que la rotación ocurre en el\(xy\) plano, la coordenada que controla este es el ángulo azimutal\(\phi\). Para los\(p_y\) orbitales\(p_x\) y, la\(\phi\) dependencia es

\[\psi_{2p_x}\sim \cos\phi \ ; \ \psi_{2p_y}\sim \sin\phi \nonumber \]

Si giramos\(2p_y\) por\(-30\) grado s (Figura 10.1.5 ; b lue es positivo y rojo es negativo), la\(\phi\) dependencia se convierte en

\[\psi_{2p_y}^{(rot)}\sim \sin(\phi +30) \nonumber \]

Figura 10.1.5 : Rotación de un\(2p_y\) orbital por\(-30\) grados.

Utilizando el hecho de que

\[\sin(\alpha \pm \beta)=\sin\alpha \cos\beta \pm cos\alpha sin\beta \nonumber \]

esta rotación da

\[\begin{align}\psi_{2p_y}^{(rot,1)} &\sim sin\phi \cos30+\cos\phi \sin30\\[4pt] &\sim \left [ \dfrac{\sqrt{3}}{2}\sin\phi +\dfrac{1}{2}\cos\phi \right ] \\[4pt] &\sim \left [ \dfrac{\sqrt{3}}{2}\psi_{2p_y}+\dfrac{1}{2}\psi_{2p_x}\right ]\end{align} \nonumber \]

Del mismo modo, considere rotar\(-\psi_{2p_y}\) por\(+30\) grados (Figura 10.1.6 ). Esto da

\[\begin{align}-\psi_{2p_y}^{(rot,2)} &\sim -\sin(\phi -30)\\[4pt] &\sim -\left [ \dfrac{\sqrt{3}}{2}\sin\phi -\dfrac{1}{2}\cos\phi \right ] \\[4pt] &\sim -\dfrac{\sqrt{3}}{2}\psi_{2p_y}+\dfrac{1}{2}\psi_{2p_x}\end{align} \nonumber \]

Figura 10.1.6 : Rotación de un\(-2p_y\) orbital por\(30\) grados.

Entonces, ahora tomamos los orbitales híbridos para que sean de la forma

\[\begin{align}\chi_1 (r) &= a\psi_{2s}(r)-b\psi_{2p_x}\\[4pt] \chi_2 (r) &= c\psi_{2s}(r)+d\psi_{2p_y}^{(rot,1)}(r)\\[4pt] \chi_3 (r) &=c\psi_{2s}(r)-d\psi_{2p_y}^{(rot,2)}(r)\end{align} \nonumber \]

Los coeficientes\(a\),\(b\), y\(c\) se determinan requiriendo que los orbitales estén normalizados y mutuamente ortogonales:

\[\begin{align}\int |\chi_1 (r)|^2 dV=1 \ &; \ \int \chi_{1}^{*}(r)\chi_2 (r)dV=0\\[4pt] \int |\chi_2 (r)|^2 dV=1 \ &; \ \int \chi_{1}^{*}(r)\chi_3 (r)dV=0\\[4pt] \int |\chi_3 (r)|^2 dV=1 \ &; \ \int \chi_{2}^{*}(r)\chi_3 (r)dV=0\end{align} \nonumber \]

Realizando el álgebra, obtenemos los siguientes orbitales\(sp^2\) híbridos:

\[\begin{align}\chi_1 (r) &= \dfrac{1}{\sqrt{3}}[\psi_{2s}(r)-\sqrt{2}\psi_{2p_x}(r)]\\[4pt] \chi_2 (r) &= \dfrac{1}{\sqrt{6}}[\sqrt{2}\psi_{2s}(r)+\psi_{2p_x}(r)+\sqrt{3}\psi_{2p_y} (r)]\\[4pt] \chi_3 (r) &= \dfrac{1}{\sqrt{6}}[\sqrt{2}\psi_{2s}(r)+\psi_{2p_x}(r)-\sqrt{3}\psi_{2p_y}(r)]\end{align} \nonumber \]

Los\(sp^2\) híbridos permiten la unión en\(120^\circ\) grados, y estos orbitales aparecen como se muestra en la Figura 10.1.7 :

Figura 10.1.7 : Formación de orbitales híbridos sp ². La combinación de un ns y dos np orbitales atómicos da tres orbitales híbridos sp ² equivalentes en una disposición plana trigonal; es decir, orientados a 120° entre sí.

La figura también muestra los solapamientos de estos orbitales con el\(1s\) orbitals of \(H\).

\(sp^3\)Orbitales Híbridos

Finalmente, consideramos el caso del metano\(CH_4\). La configuración electrónica de\(C\) es\(1s^2 2s^2 2p_x 2p_y\). Ahora promovemos uno de los\(2s\) orbitales al\(2p_z\) orbital y escribimos\(C\) como\(1s^2 2s2p_x 2p_y 2p_z\). Ahora podemos hibridar el\(2s\) orbital con cada uno de los\(2p\) orbitales para crear cuatro híbridos:

\[\begin{align}\chi_1 (r) &= \dfrac{1}{2} \left[\psi_{2s}(r)+\psi_{2p_x}(r)+\psi_{2p_y}(r)+\psi_{2p_z}(r)\right]\\[4pt] \chi_2 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)-\psi_{2p_x}(r)-\psi_{2p_y}(r)+\psi_{2p_z}(r)\right]\\[4pt] \chi_3 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)+\psi_{2p_x}(r)-\psi_{2p_y}(r)-\psi_{2p_z}(r)\right]\\[4pt] \chi_4 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)-\psi_{2p_x}(r)+\psi_{2p_y}(r)-\psi_{2p_z}(r)\right]\end{align} \nonumber \]

Los grandes lóbulos de los orbitales hibridados están orientados hacia los vértices de un tetraedro, con ángulos de 109.5° entre ellos (Figura 10.1.8 ). Como todos los orbitales hibridados discutidos anteriormente, se prevé que los orbitales atómicos híbridos sp ³ sean iguales en energía.

Figura 10.1.8 : Formación de orbitales híbridos sp ³. Combinando un ns y tres np orbitales atómicos resulta en cuatro orbitales híbridos sp ³ orientados a 109.5° entre sí en una disposición tetraédrica.

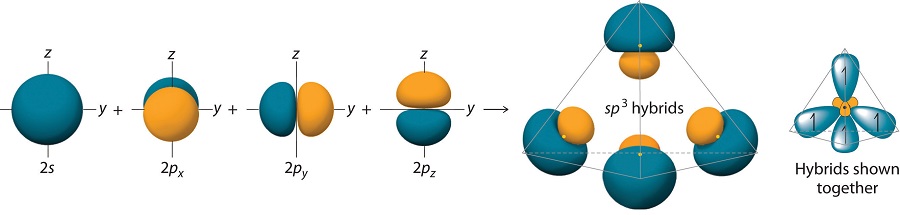
Además de explicar por qué algunos elementos forman más enlaces de los esperados en función de sus configuraciones de electrones de valencia, y por qué los enlaces formados son iguales en energía, la teoría de los enlaces de valencia explica por qué estos compuestos son tan estables: la cantidad de energía liberada aumenta con el número de enlaces formados. En el caso del carbono, por ejemplo, se libera mucha más energía en la formación de cuatro enlaces que dos, por lo que los compuestos de carbono con cuatro enlaces tienden a ser más estables que aquellos con solo dos. El carbono sí forma compuestos con solo dos enlaces covalentes (como CH ₂ o CF ₂), pero estas especies son intermedios altamente reactivos e inestables que se forman solo en ciertas reacciones químicas.

¿Son reales los orbitales híbridos?

La hibridación es un concepto a menudo mal concebido. Sólo se trata de una interpretación matemática, que explica una cierta situación de vinculación (de manera intuitiva). En una molécula la geometría de equilibrio será el resultado de diversos factores, como interacciones estéricas y electrónicas, y más interacciones adicionales con el entorno como un solvente o campo externo. La disposición geométrica no se formará porque una molécula se hibrida de cierta manera, es al revés, es decir, resultado de la geometría o más precisa e interpretación de la función de onda para el arreglo molecular dado.

La justificación que dimos para invocar la hibridación en moléculas como BeH ₂, BF ₃ y CH ₄ fue que los enlaces en cada uno son geométrica y químicamente equivalentes, mientras que los orbitales atómicos s y p en los átomos centrales no lo son. Al combinarlos en nuevos orbitales de los tipos sp, sp ² y sp ³ obtenemos el número requerido de orbitales completamente equivalentes. Esto parecía bastante fácil de hacer en papel; simplemente dibujamos cajitas y escribimos “sp ²” o lo que sea debajo de ellas. Pero, ¿qué está pasando realmente aquí?

La respuesta completa está más allá del alcance de este curso, por lo que sólo podemos ofrecer la siguiente explicación muy general. Primero, recordemos lo que entendemos por “orbital”: una función matemática ψ que tiene el carácter de una onda estacionaria cuyo cuadrado ψ ² es proporcional a la probabilidad de encontrar el electrón en cualquier ubicación particular en el espacio. Esta última, la distribución de la densidad electrónica, se puede observar (por dispersión de rayos X, por ejemplo), y en este sentido es lo único que es “real”.

Una onda estacionaria dada (función Y) se puede sintetizar combinando todo tipo de patrones de onda fundamentales (es decir, orbitales atómicos) de la misma manera que un color que observamos se puede reproducir combinando diferentes conjuntos de colores primarios en diversas proporciones. En ningún caso se deduce que estos orbitales originales (o colores) estén realmente presentes en el producto final. Entonces bien se podría argumentar que los orbitales híbridos no son “reales”; simplemente resultan convenientes para entender la unión de moléculas simples a nivel elemental, y es por eso que los usamos.

Resumen

La forma y valecias de unión de las moléculas poliatómicas pueden ser contabilizadas por orbitales híbridos. Los orbitales moleculares se forman a partir de combinaciones lineales de orbitales atómicos que son similares en energía. Estos orbitales atómicos podrían provenir de diferentes átomos, o del mismo átomo. Por ejemplo, los 2 orbitales 2patómicos de arena están muy cerca energéticamente. Cuando se forma un combo lineal de más de un orbital atómico del mismo átomo, tenemos un orbital híbrido

Colaboradores

• Mark Tuckerman (New York University)