19.1: Panorama general de la termodinámica clásica
- Page ID
- 79445
Uno de los pioneros en el campo de la termodinámica moderna fue James P. Joule (1818 - 1889). Entre los experimentos que Joule llevó a cabo, estuvo un intento de medir el efecto sobre la temperatura de una muestra de agua que fue causado por realizar trabajos sobre el agua. Usando un aparato inteligente para realizar trabajos sobre el agua usando un peso descendente para girar las paletas dentro de un bote aislado lleno de agua, Joule pudo medir un aumento de temperatura en el agua.

Así, Joule pudo demostrar que el trabajo y el calor pueden tener el mismo efecto sobre la materia, ¡un cambio de temperatura! Entonces sería razonable concluir que la calefacción, así como realizar trabajos en un sistema aumentarán su contenido energético, y así es la capacidad de realizar trabajos en los alrededores. Esto lleva a un constructo importante de la Primera Ley de la Termodinámica:
La capacidad de un sistema para hacer trabajo se incrementa calentando el sistema o haciendo trabajo en él.
La energía interna (U) de un sistema es una medida de su capacidad para suministrar energía que puede hacer trabajo dentro del entorno, haciendo de U la variable ideal para realizar un seguimiento del flujo de calor y energía de trabajo dentro y fuera de un sistema. Los cambios en la energía interna de un sistema (\(\Delta U\)) pueden calcularse mediante
\[\Delta U = U_f - U_i \label{FirstLaw}\]
donde los subíndices\(i\) e\(f\) indican estados inicial y final del sistema. \(U\)como resulta, es una variable de estado. En otras palabras, la cantidad de energía disponible en un sistema para ser suministrada al entorno es independiente de cómo esa energía llegó a estar disponible. Eso es importante porque la manera en que se transfiere la energía depende del camino.
Hay dos métodos principales que la energía puede ser transferida hacia o desde un sistema. Estos se sugieren en el enunciado anterior de la primera ley de la termodinámica. Matemáticamente, podemos reafirmar la primera ley como
\[\Delta U = q + w\]
o
\[dU = dq + dw\]
donde q se define como la cantidad de energía que fluye hacia un sistema en forma de calor y w es la cantidad de energía perdida debido a que el sistema realiza trabajos en los alrededores.
Calor
El calor es el tipo de energía que a falta de otros cambios tendría el efecto de cambiar la temperatura del sistema. Un proceso en el que el calor fluye hacia un sistema es endotérmico desde el punto de vista del sistema (q sistema > 0, q alrededores < 0). Asimismo, un proceso en el que el calor fluye fuera del sistema (hacia el entorno) se denomina exotérmico (q sistema < 0, q entorno > 0). En ausencia de cualquier flujo de energía en la forma o trabajo, el flujo de calor dentro o fuera de un sistema puede medirse por un cambio de temperatura. En los casos en los que es difícil medir los cambios de temperatura del sistema directamente, la cantidad de energía térmica transferida en un proceso puede medirse utilizando un cambio en la temperatura de los sondeos. (Este concepto se utilizará más adelante en la discusión de la calorimetría).
Una cantidad infinitesimal de flujo de calor dentro o fuera de un sistema puede estar relacionada con un cambio en la temperatura por
\[dq = C dT\]
donde C es la capacidad calorífica y tiene la definición
\[ C = \dfrac{dq}{\partial T}\]
Las capacidades de calor generalmente tienen unidades de (J mol -1 K -1) y magnitudes iguales al número de J necesarias para elevar la temperatura de 1 mol de sustancia en 1 K. Similar a una capacidad calorífica es un calor específico el cual se define por unidad de masa en lugar de por mol. El calor específico del agua, por ejemplo, tiene un valor de 4.184 J g -1 K -1 (a presión constante — una distinción de trayectoria que se discutirá más adelante.)
Ejemplo\(\PageIndex{1}\): Heat required to Raise Temperature
Ejemplo:
¿Cuánta energía se necesita para elevar la temperatura de 5.0 g de agua de 21.0 °C a 25.0 °C?
Solución:
\[q=mC \Delta T\]
\[ q = (5.0 \,\cancel{g}) (4.184 \dfrac{J}{\cancel{g} \, \cancel{°C}}) (25.0 \cancel{°C} - 21.0 \cancel{°C})\]
\[ q= 84\, J\]
¿Qué es una derivada parcial?
Una derivada parcial, como una derivada total, es una pendiente. Da una magnitud en cuanto a la rapidez con que una función cambia de valor cuando una de las variables dependientes cambia. Matemáticamente, una derivada parcial se define para una función\(f(x_1,x_2, \dots x_n)\) por
\[\left( \dfrac{ \partial f}{\partial x_i} \right)_{x_j \neq i} = \lim_{\Delta _i \rightarrow 0} \left( \dfrac{f(x_1,x_2, \dots \Delta x_i, \dots x_n) -f(x_1,x_2, \dots x_i, \dots x_n) }{\Delta x_i} \right)\]
Debido a que mide cuánto cambia una función por un cambio en una variable dependiente dada, los cambios infinitesimales en el en la función pueden describirse mediante
\[ df = \sum_i \left( \dfrac{\partial f}{\partial x_i} \right)_{x_j \neq i}\]
Para que cada contribución al cambio total en la función\(f\) pueda considerarse por separado.
Por simplicidad, considera un gas ideal. La presión se puede calcular para el gas usando la ley de gas ideal. En esta expresión, la presión es función de la temperatura y el volumen molar.
\[ p(V,T) = \dfrac{RT}{V} \]
Las derivadas parciales de p también se pueden expresar en términos de T y V.
\[ \left( \dfrac{\partial p}{ \partial V} \right)_{T} = - \dfrac{RT}{V^2} \label{max1}\]
y
\[ \left( \dfrac{\partial p}{ \partial T} \right)_{V} = \dfrac{R}{V} \label{max2}\]
Para que se pueda expresar el cambio en la presión
\[ dp = \left( \dfrac{\partial p}{ \partial V} \right)_{T} dV + \left( \dfrac{\partial p}{ \partial T} \right)_{V} dT \label{eq3}\]
o sustituyendo las ecuaciones\ ref {max1} y\ ref {max2}
\[ dp = \left( - \dfrac{RT}{V^2} \right ) dV + \left( \dfrac{R}{V} \right) dT\]
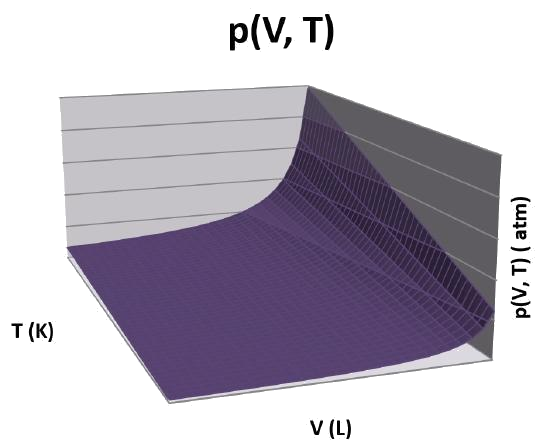
Los cambios macroscópicos se pueden expresar integrando las piezas individuales de la Ecuación\ ref {eq3} en intervalos apropiados.
\[ \Delta p = \int_{V_1}^{V_2} \left( \dfrac{\partial p}{ \partial V} \right)_{T} dV + \int_{T_1}^{T_2} \left( \dfrac{\partial p}{ \partial T} \right)_{V} dT \]
Esto se puede considerar como dos cambios consecutivos. El primero es una expansión isotérmica (temperatura constante) de\(V_1\) a\(V_2\) a\(T_1\) y el segundo es un cambio de temperatura isocórico (volumen constante) de\(T_1\) a\(T_2\) at\(V_2\). Por ejemplo, supongamos que se necesita calcular el cambio de presión para un gas ideal expandiéndose de 1.0 L/mol a 200 K a 3.0 L/mol a 400 K. La disposición podría verse de la siguiente manera.
\[ \Delta p = \underbrace{ \int_{V_1}^{V_2} \left( - \dfrac{RT}{V^2} \right ) dV}_{\text{isothermal expansion}} + \underbrace{ \int_{T_1}^{T_2}\left( \dfrac{R}{V} \right) dT}_{\text{isochoric heating}} \]
o
\[ \Delta p = \int_{1.0 \,L/mol}^{3.0 \,L/mol} \left( - \dfrac{R( 400\,K)}{V^2} \right ) dV + \int_{200 \,K}^{400,\ K }\left( \dfrac{R}{1.0 \, L/mol} \right) dT \]
\[ \Delta p = \left[ \dfrac{R(200\,K)}{V} \right]_{ 1.0\, L/mol}^{3.0\, L/mol} + \left[ \dfrac{RT}{3.0 \, L/mol} \right]_{ 200\,K}^{400\,K} \]
\[ \Delta p = R \left[ \left( \dfrac{200\,K}{3.0\, L/mol} - \dfrac{200\,K}{1.0\, L/mol}\right) + \left( \dfrac{400\,K}{3.0\, L/mol} - \dfrac{200\,K}{3.0\, L/mol}\right) \right] \]
\[ = -5.47 \, atm\]
Alternativamente, se podría calcular el cambio como un cambio isocórico de temperatura de T1 a T2 en V 1 seguido de una expansión isotérmica de V 1 a V 2 en T 2:
\[ \Delta p = \int_{T_1}^{T_2}\left( \dfrac{R}{V} \right) dT + \int_{V_1}^{V_2} \left( - \dfrac{RT}{V^2} \right ) dV \]
o r
\[ \Delta p = \int_{200 \,K}^{400,\ K }\left( \dfrac{R}{1.0 \, L/mol} \right) dT + \int_{1.0 \,L/mol}^{3.0 \,L/mol} \left( - \dfrac{R( 400\,K)}{V^2} \right ) dV \]
\[ \Delta p = \left[ \dfrac{RT}{1.0 \, L/mol} \right]_{ 200\,K}^{400\,K} + \left[ \dfrac{R(400\,K)}{V} \right]_{ 1.0\, L/mol}^{3.0\, L/mol} \]
\[ \Delta p = R \left[ \left( \dfrac{400\,K}{1.0\, L/mol} - \dfrac{200\,K}{1.0\, L/mol}\right) + \left( \dfrac{400\,K}{3.0\, L/mol} - \dfrac{400\,K}{1.0\, L/mol}\right) \right] \]
\[ = -5.47 \, atm\]
Este resultado demuestra una propiedad importante de la presión en que la presión es una variable de estado, y por lo tanto el cálculo de los cambios en la presión no depende de la vía!
Trabajo
El trabajo puede tomar varias formas, como expansión contra una presión de resistencia, extender la longitud contra una tensión de resistencia (como estirar una banda de goma), estirar una superficie contra una tensión superficial (como estirar un globo a medida que se infla) o empujar electrones a través de un circuito contra una resistencia. La clave para definir el trabajo que fluye en un proceso es comenzar con una cantidad infinitesimal de trabajo definida por lo que está cambiando en el sistema.
| Tipo de trabajo | Desplazamiento | Resistencia | dw |
|---|---|---|---|
| Expansión | dV (volumen) | - p ext (presión) | - p ext dV |
| Eléctricos | dQ (cargo) | W (resistencia) | -W dQ |
| Extensión | dL (longitud) | -t (tensión) | t dL |
| Estiramiento | dA | -s (surf. decenas.) | s dA |
El patrón seguido es siempre un desplazamiento infinitesimal multiplicado por una fuerza de resistencia. El trabajo total se puede determinar integrando a lo largo del camino que sigue el cambio.
Ejemplo\(\PageIndex{2}\): Work from a Gas Expansion
¿Cuál es el trabajo realizado por 1.00 mol un gas ideal expandiéndose de un volumen de 22.4 L a un volumen de 44.8 L contra una presión externa constante de 0.500 atm?
Solución
\[dw = -p_{ext} dV \nonumber\]
ya que la presión es constante, podemos integrarnos fácilmente para obtener un trabajo total
\[w = -p_{exp} \int_{V_1}^{V_2} dV \nonumber\]
\[w = -p_{exp} ( V_2-V_1) \nonumber\]
\[w = -(0.500 \,am)(44.8 \,L - 22.4 \,L) \left(\dfrac{8.314 \,J}{0.08206 \,atm\,L}\right) \nonumber\]
\[ = -1130 \,J = -1.14 \;kJ \nonumber\]
Nota: ¡La relación de constantes de ley de gas se puede utilizar para convertir entre ATM∙L y J de manera bastante conveniente!

