Inicio
Química
Química Física y Teórica
Química Física (LibreTexts)
19: La Primera Ley de la Termodinámica
19.10: Las entalpías relativas se pueden determinar a partir de datos de capacidad térmica y calores de transición

19.10: Las entalpías relativas se pueden determinar a partir de datos de capacidad térmica y calores de transición

Última actualización
Guardar como PDF

Page ID: 79402

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Cabe destacar que no hay entalpías absolutas. Todo lo que se define correctamente son diferencias en entalpía ΔH y estas solo se definen para procesos

Cuando se trata de entalpías

Definir el proceso

Por ejemplo para el proceso de:

Proceso 1: calentar hielo de -20 ^o C a -0 ^o C

Podríamos escribir ΔH ₁ = ∫ C _{P, hielo}. dT de T=253K a T=273K = H (273) -H (253). Pero antes de ir más allá del punto de fusión primero debe tener lugar un proceso diferente, el de

Proceso 2: fusión

Esto nos da Δ _fus H = H _líquido - H _sólido (¡ambos a 273K!). Cuando calentamos más el agua líquida para decir +20 ^o C tendríamos que integrar sobre la capacidad calorífica del líquido.

Proceso 3: calentar agua de 0 ^o C a +20 ^o C

Podríamos escribir

\[ΔH_3 = \int C_{P,water} dT \nonumber \]

de T=273K a T=293K = H (293) -H (273).

El cambio total en la entalpía entre -20 y +20 sería la suma de los tres cambios de entalpía.

\[ΔH_{total process} = ΔH_1 + Δ_{fus}H + ΔH_3 \nonumber \]

Por supuesto que podríamos considerar hacer el mismo cálculo para cualquier temperatura entre -20 y +20 y resumir todos nuestros resultados en una gráfica. Por lo tanto, los tres procesos pueden mostrarse esquemáticamente en la Figura 19.10.1 .

Figura 19.10.1 : Función de entalpía esquemática que muestra el salto en el punto de fusión

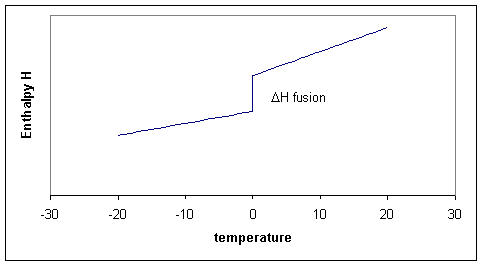
Observe que las pendientes (¡es decir, las capacidades de calor!) antes y después del punto de fusión difieren. La pendiente para el líquido es un poco más pronunciada debido a que el líquido tiene más grados de libertad y por lo tanto la capacidad calorífica del líquido tiende a ser mayor que la del sólido. En la figura las curvas cautivadoras se muestran como líneas rectas. Este sería el caso si las capacidades de calor son constantes a lo largo del intervalo de temperatura. Aunque C _p suele ser una función 'lenta' o 'débil' de la temperatura, generalmente cambia un poco, lo que significa que las líneas rectas para H se convierten en curvas.

Aunque _Cp es típicamente una función 'lenta' o 'débil' de la temperatura y se aproxima bien como una constante.

Observe que para el proceso dos, la temperatura es constante, eso significa que\(ΔT\) o\(dT\) es cero, pero ΔH es finita, en consecuencia ΔH/ΔT es infinitamente grande. Tomando el límite para ΔT yendo a cero, obtenemos una derivada:

\[ \left( \dfrac{\partial H}{ \partial T} \right)_p = C_p \nonumber \]

Esta derivada, la capacidad calorífica debe sufrir una singularidad: la pendiente es infinitamente grande (es decir, la\(H\) curva va hacia arriba). Cuando hay más transiciones de fase, más discontinuidades\(H\) y singularidades en\(C_p\) resultado (Figura 19.10.1 ). Tenga en cuenta que\(H(T)-H(0)\), no\(H(T)\) se traza para evitar la pregunta cuál es la entalpía absoluta.

Calorimetría de barrido

Existe una técnica que nos permite medir la capacidad calorífica en función de la temperatura de manera bastante directa. Se llama Calorimetría Diferencial de Barrido (DSC). Se pone una muestra en una cacerola pequeña y se pone la sartén más una sartén de referencia vacía en el calorímetro. El instrumento calienta ambas bandejas con una velocidad de calentamiento constante. Ambas sartenes se calientan por conducción, pero la capacidad de calor de la sartén llena es obviamente mayor. Esto significa que el flujo de calor en el recipiente de muestra debe ser un poco más grande que en el vacío. Este flujo de calor diferencial induce una pequeña diferencia de temperatura ΔT entre las dos bandejas que se pueden medir. Esta diferencia de temperatura es proporcional a la diferencia de flujo de calor que es proporcional a la diferencia de capacidad calorífica.

\[ΔT ~ ΔΦ ~ Δ_{between pans}C_p = C_p^{sample} \,(if the pans cancel) \nonumber \]

Sin embargo, hay una serie de serios problemas de ampliación con la técnica. Si fundes algo nunca llegarás a ver la infinita singularidad de la capacidad calorífica. En cambio, se ensancha en un pico. Si integras el pico obtienes la Δ _fusión H y el inicio se calibra para darte el punto de fusión.

alt — La señal de capacidad calorífica ideal y su señal DSC ampliada

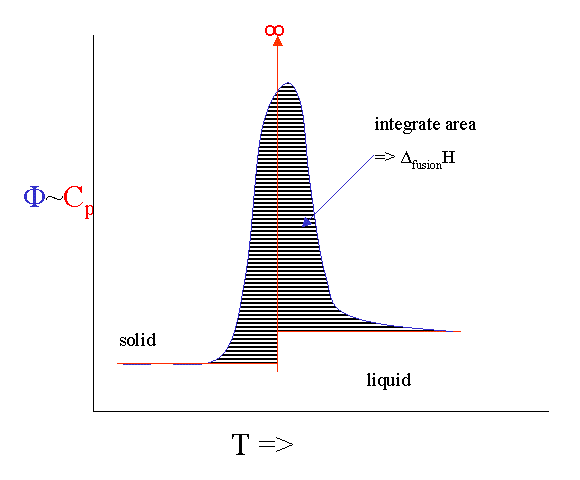
Incluso es posible calentar la muestra con una tasa que fluctúa con un poco de onda sinusoidal. Esta versión de “DSC modulada” puede incluso darte la (pequeña) diferencia en\(C_p\) antes y después del evento de fusión.