21.2: La 3ª Ley de la Termodinámica pone a la Entropía en una Escala Absoluta

En el improbable caso de que tengamos\(C_p\) datos desde 0 K podríamos escribir:

\[ S(T) = S(0) + \int_{0}^{T} C_p dT \nonumber \]

Es tentador establecer el\(S(0)\) a cero y hacer que la entropía sea así una cantidad absoluta. Como hemos visto con la entalpía, en realidad no era posible ponerla\(H(0)\) a cero. Todo lo que hicimos fue definir\(ΔH\) para un proceso en particular, aunque si hay\(C_p\) datos disponibles podríamos construir una función de entalpía (aunque con un punto cero flotante) mediante la integración de\(C_P\) (¡en lugar de\(C_p/T\)!).

Aún para la entropía\(S\) la situación es un poco diferente a la de\(H\). Aquí podemos realmente poner las cosas en una escala absoluta. Tanto Nernst como Planck se han propuesto hacerlo. Nernst postuló que para un cristal puro y perfecto\(S\) debería de hecho ir a cero como\(T\) va a cero. Por ejemplo, el azufre tiene dos estructuras cristalinas sólidas, rómbica y monoclínica. A 368.5 K, la entropía de la transición de fase de rómbica a monoclínica,\(S_{(rh)}\rightarrow S_{(mono)}\), es:

\[\Delta_\text{trs}S(\text{368.5 K})=1.09\;\sf\frac{J\cdot mol}{K} \nonumber \]

A medida que la temperatura se baja a 0 K, la entropía de la transición de fase se aproxima a cero:

\[\lim_{T\rightarrow 0}\Delta_rS=0 \nonumber \]

Figura 1. Esquema que muestra la entropía de las estructuras rómbicas y monoclínicas del azufre en función de la temperatura.

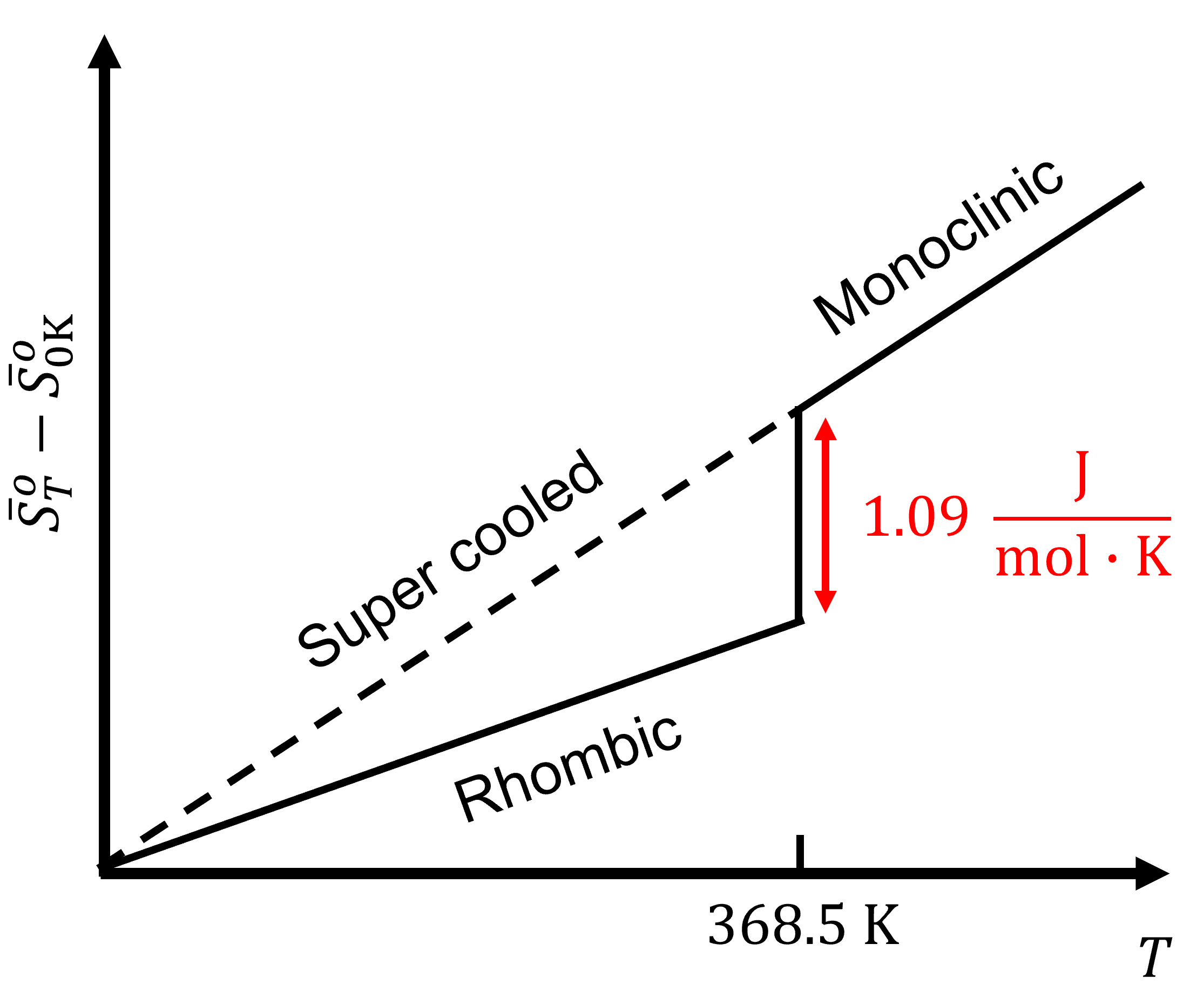
Esto demuestra que la entropía de las dos formas cristalinas son las mismas. La única manera es si todas las especies tienen la misma entropía absoluta a 0 K. Para dispersión de energía a 0 K:

1. La energía está lo más concentrada posible.
2. Sólo se pueden ocupar los estados de energía más bajos.

Para un sólido cristalino puro y perfecto a 0 K, solo hay una disposición energética para representar su estado de energía más bajo. Podemos usar esto para definir un cero natural, dando a la entropía una escala absoluta. La tercera Ley de Termodinámica establece que la entropía de una sustancia pura en una forma cristalina perfecta es de 0\(\sf\frac{J}{mol\cdot K}\) a 0 K:

\[{\bar{S}}_{0\text{ K}}^\circ=0 \nonumber \]

Esto es consistente con nuestra fórmula molecular para la entropía:

\[S=k\ln{W} \nonumber \]

Para un cristal perfecto a 0 K, el número de formas en que se puede distribuir la energía total de un sistema es one (\(W=1\)). El\(\ln{W}\) término va a cero, dando como resultado que el cristal perfecto a 0 K tenga cero entropía.

Ciertamente es cierto que para la gran mayoría de los materiales terminamos con un material cristalino a materiales suficientemente bajos (aunque hay raras excepciones como el helio líquido). No obstante, cabe mencionar que ¡un cristal completamente perfecto solo se puede cultivar a cero Kelvin! Sin embargo, no es posible cultivar nada a 0 K. A cualquier temperatura finita el cristal siempre incorpora defectos, más aún si se cultiva a temperaturas más altas. Cuando se enfrían muy lentamente los defectos tienden a ser expulsados de la red para que el cristal alcance un nuevo equilibrio con menos defectos. Esta tendencia hacia cada vez menos desorden al enfriarse es de lo que trata la tercera ley.

Sin embargo, el proceso de ordenación a menudo se vuelve imposiblemente lento, ciertamente al acercarse al cero absoluto. Esto significa que los cristales reales siempre tienen algunos congelados en imperfecciones. Así siempre hay alguna entropía residual. Afortunadamente, el efecto suele ser demasiado pequeño para medirlo. Esto es lo que nos permite ignorarlo en muchos casos (pero no en todos).

Podríamos exponer la Tercera ley de la termodinámica de la siguiente manera:

La entropía de un cristal perfecto se acerca a cero cuando T se acerca a cero (pero los cristales perfectos no existen).

Otra complicación surge cuando el sistema experimenta una transición de fase, por ejemplo, el derretimiento del hielo. Como podemos escribir:

\[Δ_{fus}H= q_P \nonumber \]

Si el hielo y el agua están en equilibrio entre sí el proceso es bastante reversible y así tenemos:

\[Δ_{fus}S = \dfrac{q_{rev}}{T}= \dfrac{Δ_{fus}H}{T} \nonumber \]

Esto quiere decir que en el punto de fusión la curva para\(S\) hace un salto repentino por esta cantidad porque todo esto sucede a una a la misma temperatura. Las entropías se calculan típicamente a partir de datos calorimétricos (\(C_P\)mediciones por ejemplo) y se tabulan en forma molar estándar. El estado estándar a cualquier temperatura es el hipotético gas ideal correspondiente a una barra para los gases.

En la tabla 21.3 se muestran varios de esos valores. Hay algunas tendencias claras. Por ejemplo, cuando el gas noble se vuelve más pesado esto induce más entropía. Esta es una consecuencia directa de la partícula en la fórmula de caja: Tiene masa en el denominador y por lo tanto los niveles de energía se abarrotan más cuando m aumenta: más niveles de energía, más entropía.

Los niveles de energía se abarrotan cuando\(m\) aumenta: más niveles de energía, más entropía

Tabulación de\(H\), \(S\) and \(G\). Frozen entropy

Hay mesas para\(H^\circ(T)-H^\circ(0)\),\(S^\circ(T)\) y\(G^\circ(T)-H^\circ(0)\) en función de la temperatura para numerosas sustancias. Como comentamos antes el plimsoll define son estado estándar en términos de presión (1 bar) y de concentración de estados de referencia, si corresponde, pero la temperatura es la de interés.

Para la mayoría de las sustancias la Tercera Ley supone que\(\lim{S^\circ(T)}\) para\(T\rightarrow 0 = 0\) es razonable pero hay notables excepciones, como el monóxido de carbono. En la forma sólida, idealmente las moléculas de monóxido de carbono deberían estar completamente ordenadas en cero absoluto, pero debido a que los tamaños de los átomos de carbono y los átomos de oxígeno están muy cerca y el dipolo de la molécula es pequeño, es muy posible poner una molécula 'boca abajo', es decir, con el oxígeno en un sitio de carbono y viceversa. A temperaturas más altas, a las que se forma el cristal, esto disminuye la energía de Gibbs (\(G\)) porque aumenta la entropía. De hecho podríamos decir que si pudiéramos poner cada molécula en la red de dos maneras diferentes, el número de formas en las\(W_{disorder}\) que podemos poner las moléculas de N en la red es de 2 ^N. Esto lleva a una contribución adicional a la entropía de

\[S_{disorder} = k\,\ln{W_{disorder}}= N k \ln 2 = R \ln 2 = 5.7\, \frac{\text{J}}{\text{mol}\cdot\text{K}}) \nonumber \]

Aunque a temperaturas más bajas el término de entropía en\(G = H-TS\) se vuelve cada vez menos significativo y el ordenamiento del cristal a un estado de menor entropía debería convertirse en un proceso espontáneo, en realidad la cinética es tan lenta que el proceso de ordenación no ocurre y el CO sólido por lo tanto tiene un valor distinto de cero entropía al acercarse a 0 K.

En principio todos los materiales cristalinos tienen este efecto hasta cierto punto, pero el CO es inusual porque la concentración de entidades 'mal alineadas' es del orden del 50% en lugar de decir 1 en 10 ¹³ (una concentración de defecto típica en digamos silicio monocristalino).