27.1: La energía cinética traslacional promedio de un gas
- Page ID
- 80384
Las leyes que describen el comportamiento de los gases estaban bien establecidas mucho antes de que alguien hubiera desarrollado un modelo coherente de las propiedades de los gases. En esta sección, presentamos una teoría que describe por qué los gases se comportan de la manera en que lo hacen. La teoría que presentamos también puede ser utilizada para derivar leyes como la ley del gas ideal a partir de principios fundamentales y las propiedades de las partículas individuales.
Una propiedad clave de las partículas individuales es su velocidad. Sin embargo, en una muestra de muchas partículas de gas, las partículas probablemente tendrán varias velocidades. En lugar de enumerar la velocidad de cada molécula de gas individual, podemos combinar estas velocidades individuales de varias maneras para obtener velocidades “colectivas” que describen la muestra como un todo.
| Inmueble | Velocidad | Energía cinética |
|---|---|---|
| Lo más probable | \( \sqrt{\dfrac{2k_bT}{m}}\) | \(k_BT\) |
| Promedio | \( \sqrt{\dfrac{8k_bT}{\pi m}}\) | \(\dfrac{4k_BT}{\pi}\) |
| Raíz media cuadrada | \( \sqrt{\dfrac{3k_bT}{m}}\) | \( \dfrac{3}{2} k_BT\) |
En el siguiente ejemplo, estas tres velocidades colectivas se definen y calculan para una muestra de gas que consta de sólo ocho moléculas.
Las velocidades de ocho moléculas fueron 1.0, 4.0, 4.0, 6.0, 6.0, 6.0, 6.0, 8.0 y 10.0 m/s, calculando su velocidad promedio (\(v_{\rm avg}\)) velocidad media cuadrática (\(v_{\rm rms}\)) y velocidad más probable (\(v_{\rm mp}\)).
Solución
Comience con definiciones:
- velocidad promedio (\(v_{\rm avg}\)) = la suma de todas las velocidades divididas por el número de moléculas
- velocidad cuadrática-media (\(v_{\rm rms}\)) = la raíz cuadrada de la suma de las velocidades cuadradas dividida por el número de moléculas
- velocidad más probable (\(v_{\rm mp}\)) = la velocidad a la que se mueve el mayor número de moléculas
La velocidad promedio:
\[\begin{align*} v_{\rm avg} &=\rm\dfrac{(1.0+4.0+4.0+6.0+6.0+6.0+8.0+10.0)\;m/s}{8} \\[4pt] &=5.6\;m/s \end{align*} \nonumber \]
La velocidad cuadrática media de la raíz:
\[\begin{align*}v_{\rm rms} &=\rm\sqrt{\dfrac{(1.0^2+4.0^2+4.0^2+6.0^2+6.0^2+6.0^2+8.0^2+10.0^2)\;m^2/s^2}{8}} \\[4pt] &=6.2\;m/s\end{align*} \nonumber \]
La velocidad más probable:
De las ocho moléculas, tres tienen velocidades de 6.0 m/s, dos tienen velocidades de 4.0 m/s, y las otras tres moléculas tienen velocidades diferentes. De ahí
\[v_{\rm mp}=6.0\, m/s. \nonumber \]
Usar expresiones para\(v_{mp}\),\(v_{ave}\), o\(v_{rms}\), es bastante simple derivar expresiones para energía cinética a partir de la expresión
\[E_{kin} = \dfrac{1}{2} mv^2 \nonumber \]
Es importante recordar que habrá una distribución completa de velocidades moleculares en una muestra termalizada de gas. Algunas moléculas viajarán más rápido y otras más despacio. También es importante reconocer que los términos de energía cinética más probables, promedio y RMS que pueden derivarse de la teoría molecular cinética no dependen de la masa de las moléculas (Cuadro 27.1.1). Como tal, se puede concluir que la energía cinética promedio de las moléculas en una muestra termalizada de gas depende únicamente de la temperatura. Sin embargo, la velocidad promedio depende de la masa molecular. Entonces, para una temperatura dada, las moléculas ligeras viajarán más rápido en promedio que las moléculas más pesadas.
Los cálculos realizados en el Ejemplo 27.1.1 se vuelven engorrosos a medida que aumenta el número de moléculas en la muestra de gas. Así, se requiere una manera más eficiente de determinar las diversas velocidades colectivas para una muestra de gas que contenga un gran número de moléculas.
Una descripción molecular de la presión y la velocidad molecular
La teoría molecular cinética de los gases explica las leyes que describen el comportamiento de los gases. Desarrollada a mediados del siglo XIX por varios físicos, entre ellos el austriaco Ludwig Boltzmann (1844—1906), el alemán Rudolf Clausius (1822—1888) y el escocés James Clerk Maxwell (1831—1879), esta teoría se basa en las propiedades de las partículas individuales definidas para un gas ideal y lo fundamental conceptos de física. Así, la teoría molecular cinética de los gases proporciona una explicación molecular para las observaciones que condujeron al desarrollo de la ley de gases ideales. La teoría molecular cinética de los gases se basa en los siguientes cinco postulados:
- Un gas está compuesto por un gran número de partículas llamadas moléculas (ya sean monatómicas o poliatómicas) que están en constante movimiento aleatorio.
- Debido a que la distancia entre las moléculas de gas es mucho mayor que el tamaño de las moléculas, el volumen de las moléculas es insignificante.
- Las interacciones intermoleculares, ya sean repulsivas o atractivas, son tan débiles que también son insignificantes.
- Las moléculas de gas chocan entre sí y con las paredes del contenedor, pero estas colisiones son perfectamente elásticas; es decir, no cambian la energía cinética promedio de las moléculas.
- La energía cinética promedio de las moléculas de cualquier gas depende solo de la temperatura, y a una temperatura dada, todas las moléculas gaseosas tienen exactamente la misma energía cinética promedio.
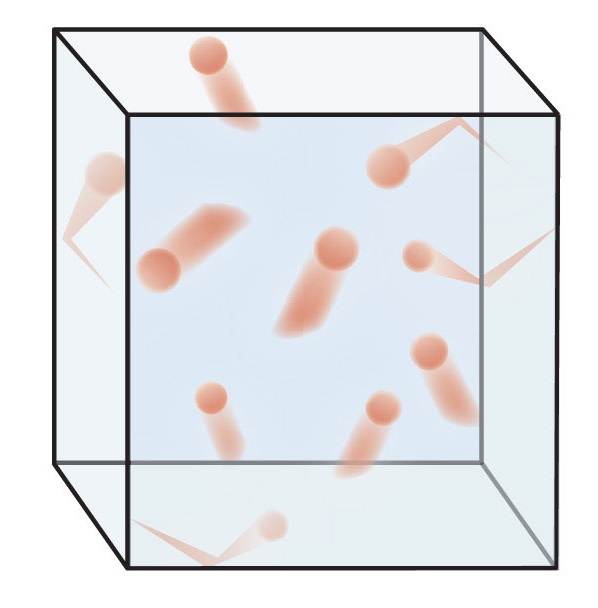
Figura 27.1.1 : Visualización del movimiento molecular. Las moléculas de un gas están en constante movimiento y chocan entre sí y con la pared del contenedor.
Si bien las moléculas de los gases reales tienen volúmenes distintos de cero y ejercen fuerzas atractivas y repulsivas unas sobre otras, por el momento nos centraremos en cómo la teoría molecular cinética de los gases se relaciona con las propiedades de los gases que hemos estado discutiendo. En el Tema 1C, explicamos cómo se debe modificar esta teoría para dar cuenta del comportamiento de los gases reales.
Los postulados 1 y 4 establecen que las moléculas de gas están en constante movimiento y chocan frecuentemente con las paredes de sus contenedores. La colisión de moléculas con las paredes de sus contenedores da como resultado una transferencia de impulso (impulso) de las moléculas a las paredes (Figura 27.1.2 ).
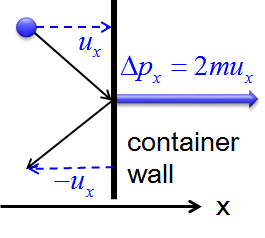
Figura 27.1.2 : Nota: En esta figura, el símbolo\(u\) se utiliza para representar la velocidad. En el resto de este texto, la velocidad se representará con el símbolo\(v\). Transferencia de Momentum (Impulso) de una molécula a la pared del contenedor a medida que rebota en la pared. La transferencia de momento (\(\Delta \rho_x\)) para una colisión elástica es igual a m\(\Delta v_x\), donde m es la masa de la molécula y\(\Delta v_x\) es el cambio en el\(x\) componente de la velocidad molecular (\(v_{x_{final}}-v_{x_{initial}})\). El muro es perpendicular a\(x\) axis. Dado que las colisiones son elásticas, la molécula rebota con la misma velocidad en la dirección opuesta, y\(\Delta v_x\) es igual\(2v_x\).
La transferencia de impulso a la pared perpendicular al\(x\) eje como una molécula con una velocidad inicial\(v_x\) en la\(x\) dirección de impactos se expresa como:
\[\rm momentum\; transfer_x\;= \Delta \rho_x = m\Delta v_x = 2mv_x \label{1.2.1} \]
La frecuencia de colisión, un número de colisiones de las moléculas a la pared por unidad de área y por segundo, aumenta con la velocidad molecular y el número de moléculas por unidad de volumen.
\[f\propto (v_x) \times \Big(\dfrac{N}{V}\Big) \label{1.2.2} \]
La presión que ejerce el gas sobre la pared se expresa como el producto del impulso y la frecuencia de colisión.
\[P\propto (2mv_x)\times(v_x)\times\Big(\dfrac{N}{V}\Big)\propto \Big(\dfrac{N}{V}\Big)mv_x^2 \label{1.2.3} \]
En cualquier instante, sin embargo, las moléculas en una muestra de gas están viajando a diferente velocidad. Por lo tanto, debemos sustituir\(v_x^2\) en la expresión anterior con el valor promedio de\(v_x^2\), que se denota por\(\bar{v_x^2}\). La barra superior designa el valor promedio sobre todas las moléculas.
La expresión exacta para la presión se da como:
\[P=\dfrac{N}{V}m\bar{v_x^2} \label{1.2.4} \]
Por último, debemos considerar que no hay nada de especial en\(x\) la dirección. Eso debemos esperar\(\bar{v_x^2}= \bar{v_y^2}=\bar{v_z^2}=\dfrac{1}{3}\bar{v^2}\). Aquí la cantidad\(\bar{v^2}\) se llama la velocidad media cuadrada definida como el valor promedio de velocidad cuadrada (\(v^2\)) sobre todas las moléculas. Ya que\(v^2=v_x^2+v_y^2+v_z^2\) para cada molécula,\(\bar{v^2}=\bar{v_x^2}+\bar{v_y^2}+\bar{v_z^2}\). Al sustituir\(\bar{v_x^2}\) en\(\dfrac{1}{3}\bar{v^2}\) la expresión anterior, podemos obtener la expresión final de la presión:
\[P=\dfrac{1}{3}\dfrac{N}{V}m\bar{v^2} \label{1.2.5} \]
Debido a que los volúmenes y las interacciones intermoleculares son insignificantes, los postulados 2 y 3 establecen que todas las partículas gaseosas se comportan de manera idéntica, independientemente de la naturaleza química de sus moléculas componentes. Esta es la esencia de la ley de gas ideal, que trata a todos los gases como colecciones de partículas que son idénticas en todos los aspectos excepto en masa. El Postulado 2 también explica por qué es relativamente fácil comprimir un gas; simplemente se disminuye la distancia entre las moléculas de gas.
El Postulado 5 proporciona una explicación molecular de la temperatura de un gas. El postulado 5 se refiere a la energía cinética traduccional promedio de las moléculas de un gas,
\[\epsilon = m\bar{v^2}/2\label{1.2.6} \]
Reordenando la ecuación\(\ref{1.2.5}\) y sustituyendo en ecuación\(\ref{1.2.6}\), obtenemos
\[PV = \dfrac{1}{3} N m \bar{v^2} = \dfrac{2}{3} N \epsilon \label{1.2.7} \]
El factor 2/3 en la proporcionalidad refleja el hecho de que los componentes de velocidad en cada una de las tres direcciones contribuyen ½ kT a la energía cinética de la partícula. La energía cinética traslacional promedio es directamente proporcional a la temperatura:
\[\epsilon = \dfrac{3}{2} kT \label{1.2.8} \]
en la que la constante de proporcionalidad\(k\) se conoce como la constante de Boltzmann. Sustitución de\(\ref{1.2.7}\) rendimientos de ecuación\(\ref{1.2.8}\) en ecuación
\[ PV = \left( \dfrac{2}{3}N \right) \left( \dfrac{3}{2}kT \right) =NkT \label{1.2.9} \]
La constante de Boltzmann\(k\) es solo la constante de gas por molécula, así que si se elige N como número de Avogadro\(N_A\), entonces\(N_Ak\) es R, la constante de gas por mol. Así, para n moles de partículas, la Ecuación\(\ref{1.2.9}\) se convierte en
\[ PV = nRT \label{1.2.10} \]
que es la ley de gas ideal.
Como se indica en el Ejemplo 27.1.1 , la velocidad cuadrática-media (\(v_{\rm rms}\)) es la raíz cuadrada de la suma de las velocidades cuadradas dividida por el número de partículas:
\[v_{\rm rms}=\sqrt{\bar{v^2}}=\sqrt{\dfrac{v_1^2+v_2^2+\cdots v_N^2}{N}} \label{1.2.11} \]
donde\(N\) es el número de partículas y\(v_i\) es la velocidad de la partícula\(i\).
El\(v_{\rm rms}\) para una muestra que contiene un gran número de moléculas se puede obtener combinando ecuaciones\(\ref{1.2.7}\) y de una\(\ref{1.2.8}\) manera ligeramente diferente a la utilizada para obtener la ecuación\(\ref{1.2.10}\):
\[PV=\dfrac{1}{3} N m \bar{v^2} = \dfrac{2}{3} N \epsilon \tag{27.1.10} \]
\[\epsilon = \dfrac{3}{2} kT \tag{27.1.11} \]
\[\dfrac{1}{3} N m \bar{v^2}= \left(\dfrac{2}{3}\right)\left(\dfrac{3}{2}\right) NkT \label{1.2.12} \]
\[\dfrac{1}{3} N m \bar{v^2}= NkT \label{1.2.13} \]
\[ N m \bar{v^2}= 3NkT \label{1.2.14} \]
Si se elige N para ser el número de Avogadro\(N_A\), entonces\(N_Am = M\), la masa molar, y\(N_Ak = R\), la constante de gas por mol,
\[\bar{v^2} = \dfrac{3RT}{M} \label{1.2.15} \]
\[v_{\rm rms}=\sqrt{\bar{v^2}}=\sqrt{\dfrac{3RT}{M}} \label{1.2.16} \]
En Ecuación\(\ref{1.2.16}\),\(v_{\rm rms}\) tiene unidades de metros por segundo; en consecuencia, las unidades de masa molar\(M\) son kilogramos por mol, la temperatura\(T\) se expresa en kelvin, y la constante de gas ideal\(R\) tiene el valor 8.3145 J/ (K•mol). \(\ref{1.2.16}\)La ecuación muestra que\(v_{\rm rms}\) de un gas es proporcional a la raíz cuadrada de su temperatura Kelvin e inversamente proporcional a la raíz cuadrada de su masa molar. La velocidad media cuadrática de la raíz de un gas aumenta con el aumento de la temperatura. A una temperatura dada, las moléculas de gas más pesadas tienen velocidades más lentas que las más ligeras.
¿Cuál es la velocidad media cuadrática de\(\rm O_2\) las moléculas a 25ºC?
Dado: Temperatura en ºC, tipo de moléculas, constante de gas ideal
Preguntado por:\(v_{\rm rms}\), la velocidad media cuadrática de la raíz
Estrategia:
Convertir temperatura a kelvins:
\(\rm T\; (in\; kelvin) = (25ºC + 273ºC)\dfrac{1\; K}{1\; ºC} = 298\; K\)
Convertir masa molar de\(\rm O_2\) moléculas en kg por mol:
\(\rm M\; (in\; \dfrac{kg}{mole}) = 32.00\dfrac{g}{mole}\rm x\dfrac{1\; kg}{1000\; g}=0.03200\dfrac{kg}{mole}\)
Utilice la ecuación\(\ref{1.2.16}\) para calcular la velocidad rms.
Solución
\(v_{\rm rms_{\rm O_2}}= \sqrt{\dfrac{3\rm (8.3145\dfrac{J}{K·mole})(298.15\; K)}{\rm 0.03200\dfrac{kg}{mole}}}=482\dfrac{m}{s}\)
¿Cuál es la velocidad media cuadrática de\(\rm Cl_2\) las moléculas a 25ºC?
\(v_{\rm rms_{\rm Cl_2}}= 324\dfrac{m}{s}\)
Muchas moléculas, muchas velocidades
A temperaturas superiores al cero absoluto, todas las moléculas están en movimiento. En el caso de un gas, este movimiento consiste en saltos en línea recta cuyas longitudes son bastante grandes en comparación con las dimensiones de la molécula. Aunque nunca podemos predecir la velocidad de una molécula individual en particular, el hecho de que usualmente estemos lidiando con un gran número de ellas nos permite saber qué fracción de las moléculas tienen energías cinéticas (y por lo tanto velocidades) que se encuentran dentro de cualquier rango dado.
La trayectoria de una molécula de gas individual consiste en una serie de trayectorias en línea recta interrumpidas por colisiones. Lo que sucede cuando dos moléculas chocan depende de sus energías cinéticas relativas; en general, una molécula más rápida o más pesada impartirá parte de su energía cinética a una más lenta o más ligera. Dos moléculas que tienen masas idénticas y que se mueven en direcciones opuestas a la misma velocidad permanecerán momentáneamente inmóviles después de su colisión.
Si pudiéramos medir las velocidades instantáneas de todas las moléculas en una muestra de un gas a alguna temperatura fija, obtendríamos un amplio rango de valores. Unos pocos serían cero, y unos pocos serían velocidades muy altas, pero la mayoría caerían en un rango más o menos bien definido. Podríamos tener la tentación de definir una velocidad promedio para una colección de moléculas, pero aquí tendríamos que tener cuidado: las moléculas que se mueven en direcciones opuestas tienen velocidades de signos opuestos. Debido a que las moléculas que están en un gas están en movimiento térmico aleatorio, habrá casi tantas moléculas moviéndose en una dirección como en la dirección opuesta, por lo que los vectores de velocidad de signos opuestos se cancelarían todos y la velocidad promedio saldría a cero. Como esta respuesta no es muy útil, necesitamos hacer nuestro promedio de una manera ligeramente diferente.
El tratamiento adecuado es promediar los cuadrados de las velocidades, y luego tomar la raíz cuadrada de este valor para obtener la velocidad media cuadrática (\(v_{\rm rms}\)), que es lo que desarrollamos anteriormente. Esta velocidad describe la muestra de gas como un todo, pero no nos dice sobre el rango de velocidades posibles, ni nos dice la distribución de velocidades. Para obtener una descripción más completa de cuántas moléculas de gas probablemente viajarán a un rango de velocidad dado, necesitamos hacer uso de la ley de distribución de Maxwell-Boltzmann.
Colaboradores y Atribuciones
- Tom Neils, Grand Rapids Community College (editing)

