27.6: Trayectoria Libre Media

Energía de colisión

Considera dos partículas\(A\) y\(B\) en un sistema. La energía cinética de estas dos partículas es

\[K_{AB} = \dfrac{\textbf{p}_A^2}{2m_A} + \dfrac{\textbf{p}_B^2}{2m_B} \label{27.6.1} \]

Podemos describir la energía cinética en términos de centro de masa\(\left( \textbf{P} \right)\) y momento relativo\(\left( \textbf{p} \right)\), que vienen dados por

\(\textbf{P} = \textbf{p}_A + \textbf{p}_B\)

y

\[ \begin{align*} \textbf{p} &= \text{relative velocity}\times \mu \\[4pt] &= (\textbf{v}_A -\textbf{v}_B) \times \left(\dfrac{m_A m_B}{m_A + m_B}\right) \\[4pt] &= \dfrac{m_B \textbf{p}_A - m_A \textbf{p}_B}{M}\end{align*} \nonumber \]

donde

\(M = m_A + m_B\)

es la masa total de las dos partículas, y

\[\mu = \dfrac{m_A m_B}{M} \nonumber \]

es la masa reducida de las dos partículas.

Sustituyendo estos términos en la ecuación\(\ref{27.6.1}\), encontramos

\[K_{AB} = \dfrac{\textbf{p}_A^2}{2m_A} + \dfrac{\textbf{p}_B^2}{2m_B} = \dfrac{\textbf{P}^2}{2M} + \dfrac{\textbf{p}^2}{2 \mu} \nonumber \]

Tenga en cuenta que la energía cinética se separa en una suma de un término de centro de masa y un término de impulso relativo.

Ahora la posición relativa de las dos partículas es\(\textbf{r} = \textbf{r}_A - \textbf{r}_B\) tal que la velocidad relativa es\(\dot{\textbf{r}} = \dot{\textbf{r}}_A - \dot{\textbf{r}}_B\) o\(\textbf{v} = \textbf{v}_A - \textbf{v}_B\). Así, si las dos partículas se acercan entre sí de tal manera que\(\textbf{v}_A = - \textbf{v}_B\), entonces\(\textbf{v} = 2 \textbf{v}_A\). Sin embargo, al equiparticionar la energía cinética relativa, que es independiente de la masa, obtenemos

\[\left< \dfrac{\textbf{p}^2}{2 \mu} \right> = \dfrac{3}{2} k_B T \nonumber \]

que se llama la energía de colisión

Sección transversal de colisión

Considera dos moléculas en un sistema. La probabilidad de que colisionen aumenta con el “tamaño” efectivo de cada partícula. Sin embargo, la medida de tamaño que es relevante es el área aparente de la sección transversal de cada partícula. Por simplicidad, supongamos que las partículas son esféricas, lo que no es una mala aproximación para moléculas pequeñas. Si estamos mirando una esfera, lo que percibimos como el tamaño de la esfera es el área de sección transversal de un gran círculo. Recordemos que cada partícula esférica tiene asociada una “esfera de colisión” que solo encierra dos partículas en el contacto más cercano, es decir, en el momento de una colisión, y que esta esfera es un radio\(d\), donde\(d\) está el diámetro de cada partícula esférica. La sección transversal de esta esfera de colisión representa una sección transversal efectiva para cada partícula dentro de la cual es inminente una colisión. La sección transversal de la esfera de colisión es el área de un gran círculo, que es\(\pi d^2\). Denotamos esta aparente área de sección transversal\(\sigma\). Así, para partículas esféricas\(A\) y\(B\) con diámetros\(d_A\) y\(d_B\), las secciones transversales individuales son

\[\sigma_A = \pi d_A^2, \: \: \: \sigma_B = \pi d_B^2 \nonumber \]

La sección transversal de colisión,\(\sigma_{AB}\) está determinada por un diámetro efectivo\(d_{AB}\) característico de ambas partículas. Los incrementos de probabilidad de colisión de ambas partículas tienen diámetros grandes y disminuye si una de ellas tiene un diámetro menor que la otra. De ahí que una simple medida sensible a esto es el promedio aritmético

\[d_{AB} = \dfrac{1}{2} \left( d_A + d_B \right) \nonumber \]

y la sección transversal resultante de la colisión se convierte

\[\begin{align} \sigma_{AB} &= \pi d_{AB}^2 \nonumber\\ &= \pi \left( \dfrac{d_A + d_B}{2} \right)^2 \nonumber\\ &= \dfrac{\pi}{4} \left( d_A^2 + 2d_A d_B + d_B^2 \right) \nonumber \\ &= \dfrac{1}{4} \left( \sigma_A + 2 \sqrt{\sigma_A \sigma_B} + \sigma_B \right) \nonumber\\ &= \dfrac{1}{2} \left[ \left( \dfrac{\sigma_A + \sigma_B}{2} \right) + \sqrt{\sigma_A \sigma_B} \right] \nonumber \end{align} \nonumber \]

que, curiosamente, es un promedio de los dos tipos de promedios de las dos secciones transversales individuales, ¡las medias aritméticas y geométricas!

Frecuencia promedio de colisión

Considera un sistema de partículas con secciones transversales individuales\(\sigma\). Una partícula de sección transversal\(\sigma\) que se mueve una distancia\(l\) en un tiempo\(\Delta t\) barrerá un volumen cilíndrico (ignorando las tapas esféricas) de volumen\(\sigma l\) (Figura 27.6.1 ). Si el sistema tiene una densidad\(\rho\) numérica, entonces el número de colisiones que ocurrirán es

\[N_{\text{coll}} = \rho \sigma l \nonumber \]

Figura 27.6.1 : Cilindro de colisión. Cualquier partícula que se superponga parcialmente con este volumen experimentará una colisión con una partícula de prueba que traza este volumen. (CC BY-NC; Ümit Kaya)

Definimos la frecuencia de colisión para una sola molécula\(z_A\), también conocida como la tasa promedio de colisión como\(N_{\text{coll}}/ \Delta t\), i.e.,

\[z_A = \dfrac{N_{\text{coll}}}{\Delta t} = \dfrac{\rho \sigma l}{\Delta t} = \rho \sigma \langle v \rangle \label{27.6.2} \]

donde\(\langle v \rangle\) es la velocidad promedio de una partícula

\[\langle v \rangle = \sqrt{\dfrac{8 k_B T}{\pi m_A}} \nonumber \]

\(\ref{27.6.2}\)La ecuación no es del todo correcta porque se basa en el supuesto de que sólo se mueve la molécula de interés. Si tomamos en cuenta el hecho de que todas las partículas se mueven una respecto a la otra, y suponemos que todas las partículas son del mismo tipo (digamos, tipo\(A\)), entonces realizar el promedio sobre una distribución de velocidad Maxwell-Boltzmann da

\[\langle v_r \rangle = \sqrt{\dfrac{8 k_B T}{\pi \mu}} \nonumber \]

donde\(\mu = m_A/2\) esta la masa reducida.

Por lo tanto,

\[\langle v_r \rangle = \sqrt{2} \langle v \rangle \nonumber \]

y

\[z_A = \sqrt{2} \rho \sigma \langle v \rangle\ = \rho \sigma \langle v_r \rangle \nonumber \]

El recíproco de\(z_A\) es una medida del tiempo promedio entre colisiones para una sola molécula.

Trayectoria Media Libre

El camino libre medio es la distancia que recorrerá una partícula, en promedio, antes de experimentar un evento de colisión. Esto se define como el producto de la velocidad promedio de una partícula y el tiempo entre colisiones. El primero lo es\(\langle v \rangle \), mientras que el segundo lo es\(1/z_A\). Por lo tanto, tenemos

\[\lambda = \dfrac{\langle v\rangle}{\sqrt{2} \rho \sigma \langle v \rangle} = \dfrac{1}{\sqrt{2} \rho \sigma} \nonumber \]

El camino libre medio también se puede describir usando términos de la ley de gas ideal, porque\(\rho = \dfrac{P \cdot N_A}{R \cdot T}\):

\[\lambda = \dfrac {R \cdot T}{\sqrt{2} \cdot N_A \cdot \sigma \cdot P} \nonumber \]

Paseos Aleatorios

En cualquier sistema, una partícula que sufre frecuentes colisiones tendrá la dirección de su movimiento cambiada con cada colisión y trazará un camino que parece ser aleatorio. De hecho, si tratamos el proceso como estadístico, entonces, de hecho, estamos tratando cada evento de colisión como un evento aleatorio, ¡y la partícula cambiará su dirección en momentos aleatorios de maneras aleatorias! Tal trayectoria podría aparecer como se muestra en la Figura\(\PageIndex{2}\). Tal camino a menudo se conoce como un camino de caminata aleatorio.

Figura\(\PageIndex{2}\): Sendero de caminata aleatorio. La trayectoria de una sola partícula en una muestra de gas. Los frecuentes cambios de dirección son el resultado de colisiones con otras moléculas de gas y con las paredes del contenedor.

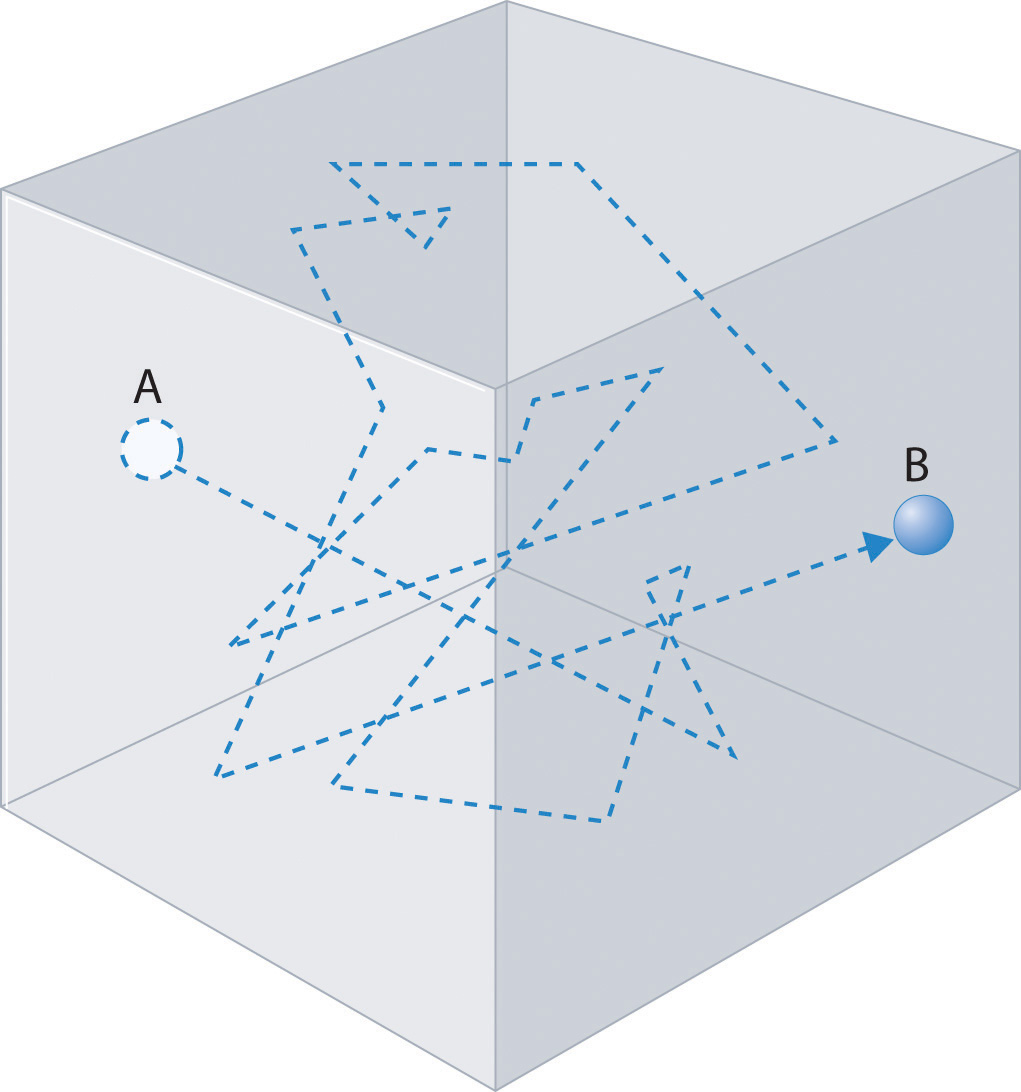
Para analizar tales caminos, consideremos un paseo aleatorio en una dimensión. Supondremos que la partícula mueve una longitud de trayectoria libre de medias\(\lambda\) entre colisiones y que cada colisión cambia la dirección del movimiento de las partículas, lo que en una dimensión, significa que la partícula se mueve ya sea hacia la derecha o hacia la izquierda después de cada evento. Esto se puede mapear en un “lanzamiento de moneda” metafórico que puede subir cabezas “H” o colas “T”, con “H” causando movimiento hacia la derecha, y “T” causando movimiento hacia la izquierda. Que haya\(N\) tales tiradas de monedas,\(i\) sea el número de veces que aparezca “H” y\(j\) denote el número de veces que aparece “T”. Así, el avance de la partícula, que definimos como movimiento neto hacia la derecha, viene dado por\((i - j) \lambda\). Dejando\(k = i - j\), esto es justo\(k \lambda\). Así, necesitamos saber cuál es la probabilidad de obtener un valor particular de\(k\) en un número muy grande\(N\) de tiradas de monedas. Denote esto\(P(k)\).

En los tirados de\(N\) monedas, el número total de secuencias posibles de “H” y “T” es\(2^N\). Sin embargo, el número de formas en las que podemos obtener\(i\) cabezas y\) j\) colas, con\(i + j = N\) es un coeficiente binomial\(N!/i!j!\). Ahora

\[j = N - i = N - (j + k) = N - j - k \nonumber \]

para que\(j = (N - k )/2\). Del mismo modo,

\[i = N - j = N - (i - k) = N - i + k \nonumber \]

para que\(i = (N + k)/2\). Por lo tanto, la probabilidad\(P(k)\) es

\[P(k) = \dfrac{N!}{2^N i! j!} = \dfrac{1}{2^N} \dfrac{N!}{\left(\dfrac{N + k}{2} \right) ! \left( \dfrac{N - k}{2} \right) !} \nonumber \]

Ahora tomamos el logaritmo de ambos lados:

\[\text{ln} \: P(k) = \: \text{ln} \: N! - \: \text{ln} \: 2^N - \: \text{ln} \: \left( \dfrac{N + k}{2} \right) ! - \: \text{ln} \: \left( \dfrac{N - k}{2} \right) ! \nonumber \]

y usa la aproximación de Stirling:

\[\text{ln} \: N! \approx N \: \text{ln} \: N - N \nonumber \]

y escribir\(\text{ln} \: P(k)\) como

\[\begin{align} \text{ln} \: P(k) &\approx N \: \text{ln} \: N - N - N \: \text{ln} \: 2 - \dfrac{1}{2} (N + k) \: \text{ln} \: \dfrac{1}{2} (N + k) + \dfrac{1}{2} (N + k) - \dfrac{1}{2} (N - k) \: \text{ln} \: \dfrac{1}{2} (N - k) + \dfrac{1}{2} (N - k) \nonumber\\ &= N \: \text{ln} \: N - N \: \text{ln} \: 2 + \dfrac{1}{2} (N + k) \: \text{ln} \: \dfrac{1}{2} - \dfrac{1}{2} (N + k) \: \text{ln} \: (N + k) - \dfrac{1}{2} (N - k) \: \text{ln} \: \dfrac{1}{2} - \dfrac{1}{2} (N - k) \: \text{ln} \: (N - k) \nonumber\\ &= N \: \text{ln} \: N - N \: \text{ln} \: 2 + \dfrac{1}{2} (N + k) \: \text{ln} \: 2 - \dfrac{1}{2} (N + k) \: \text{ln} \: (N + k) + \dfrac{1}{2} (N - k) \: \text{ln} \: 2 - \dfrac{1}{2} (N - k) \: \text{ln} \: (N - k) \nonumber\\ &= N \: \text{ln} \: N - \dfrac{1}{2} \left[ (N + k) \: \text{ln} \: (N + k) + (N - k) \: \text{ln} \: (N - k) \right] \nonumber\end{align} \nonumber \]

Ahora, escribe

\[\text{ln} \: (N + k) = \: \text{ln} \: N \left( 1 + \dfrac{k}{N} \right) = \: \text{ln} \: N + \: \text{ln} \: \left( 1 + \dfrac{k}{N} \right) \nonumber \]

y

\[\text{ln} \: (N - k) = \: \text{ln} \: N \left( 1 - \dfrac{k}{N} \right) = \: \text{ln} \: N + \: \text{ln} \: \left( 1 - \dfrac{k}{N} \right) \nonumber \]

Ahora usamos las expansiones

\[\begin{align} \text{ln} \: \left( 1 + \dfrac{k}{N} \right) &= \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 + \cdots \nonumber \\ \text{ln} \: \left( 1 - \dfrac{k}{N} \right) &= - \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 + \cdots \nonumber\end{align} \nonumber \]

Si nos detenemos en el término de segundo orden, entonces

\[\begin{align} \text{ln} \: P(k) &= N \: \text{ln} \: N - \dfrac{1}{2} (N + k) \left[ \: \text{ln} \: N + \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 \right] - \dfrac{1}{2} (N - k) \left[ \: \text{ln} \: N - \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 \right] \nonumber \\ &= -\dfrac{1}{2} (N + k) \left[ \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 \right] + \dfrac{1}{2} (N - k) \left[ \left( \dfrac{k}{N} \right) + \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 \right] \nonumber \\ &= \dfrac{1}{2} N \left( \dfrac{k}{N} \right)^2 - k \left( \dfrac{k}{N} \right) \nonumber\\ & = \dfrac{k^2}{2N} - \dfrac{k^2}{N} = - \dfrac{k^2}{2N} \nonumber\end{align} \nonumber \]

para que

\[P(k) = e^{-k^2/2N} \nonumber \]

Ahora bien, si dejamos\(x = k \lambda\) y\(L = \sqrt{N} \lambda\), y si dejamos\(x\) ser una variable aleatoria continua, entonces la distribución de probabilidad correspondiente\(P(x)\) se convierte en

\[P(x) = \dfrac{1}{L \sqrt{2 \pi}} \: e^{-x^2/2L^2} = \dfrac{1}{\sqrt{2 \pi N \lambda^2}} \: e^{-x^2/2N \lambda^2} \label{27.6.3} \]

que es una distribución gaussiana simple. Ahora bien,\(N\) es el número de colisiones, que viene dado por\(z_At\), así podemos escribir la distribución de probabilidad para que la partícula difunda una distancia\(x\) en el tiempo\(t\) como

\[P(x, t) = \dfrac{1}{\sqrt{2 \pi z_At \lambda^2}} \: e^{-x^2/2z_At \lambda^2} \nonumber \]

Definir\(D = z_A \lambda^2/2\) como la constante de difusión, que tiene unidades de (longitud)\(^{\text{2}}\)/time. The distribution then becomes

\[P(x, t) = \dfrac{1}{\sqrt{4 \pi D t }} \: e^{-x^2/4D t} \nonumber \]

Tenga en cuenta que esta distribución satisface la siguiente ecuación:

\[\dfrac{\partial}{\partial t} P(x, t) = D \dfrac{\partial^2}{\partial x^2} P(x, t) \nonumber \]

que se llama la ecuación de difusión. La ecuación de difusión es, de hecho, más general que la distribución gaussiana en la Ecuación\(\ref{27.6.3}\). It is capable of predicting the distribution in any one-dimensional geometry subject to any initial distribution \(P(x, 0)\) and any imposed boundary conditions.

En tres dimensiones, consideramos que las tres direcciones espaciales son independientes, por lo tanto, la distribución de probabilidad para que una partícula se difunda a una ubicación\(\textbf{r} = (x, y, z)\) is just a product of the three one-dimensional distributions:

\[\mathcal{P}(\textbf{r}) = P(x) \: P(y) \: P(z) = \dfrac{1}{(4 \pi D t) ^{3/2}} \: e^{-\left( x^2 + y^2 + z^2 \right)/4Dt} \nonumber \]

y si solo estamos interesados en la difusión a distancia\(r\), we can introduce spherical coordinates, integrate over the angles, and we find that

\[P(r, t) = \dfrac{4 \pi}{(4 \pi D t)^{3/2}} \: e^{-r^2/4Dt} \nonumber \]

Frecuencia total de colisión por unidad de volumen

En la ecuación 27.6.18,\(z_A\) representa la frecuencia de colisión para una molécula específica en una muestra de gas. Si se desea calcular la frecuencia de colisión total por unidad de volumen, se debe tener en cuenta la densidad numérica de las moléculas\(\rho\),,. La frecuencia de colisión total en una muestra que contiene solo moléculas A,\(Z_{AA}\), es

\[Z_{AA} = \dfrac{1}{2}\rho z_A = \dfrac{1}{2} \sigma \langle v_r \rangle \rho^2 = \dfrac{\sigma \langle v\rangle \rho^2}{\sqrt{2}}\nonumber \]

Se\(\dfrac {1}{2}\) debe incluir el factor de para evitar colisiones de doble conteo entre moléculas similares. (Este es un razonamiento idéntico al hecho de que solo hay una manera de rodar el doble 3 con dos dados).

Si tiene una muestra de gas que contiene moléculas A y moléculas B, entonces

\[Z_{AB} = \sigma_{AB} \langle v_r \rangle \rho_A \rho_B \label{27.6.4} \]

donde

\(\sigma_{AB} = \pi \left (\dfrac{d_A + d_B}{2} \right)^2 \)y\(\langle v_r \rangle = \sqrt{\dfrac{8 k_B T}{\pi \mu}} \nonumber\)

Ejemplo\(\PageIndex{1}\)

Calcular la frecuencia de colisiones hidrógeno-hidrógeno en un contenedor de 1.00 centímetros cúbicos a 1.00 bar y 298 K.

Solución

El valor de\(\sigma_{H_2}\) es 2.30 x 10 ^-19 m ².

La densidad numérica es\(\rho = \left(\dfrac{N_AP_{H_2}}{RT} \right) = \left(\dfrac{(6.022x10^{23} mole^{-1})(1.00 bar)}{(0.08314 L·bar·mol^{-1}·K^{-1})(298 K)} \right) = 2.43 x 10^{22} L^{-1} = 2.43 x 10^{25} m^{-3} \)

La velocidad promedio es\(\langle \text v\rangle = \sqrt{\dfrac{8 \text{R T}}{\pi \text{M}}} = \sqrt{\left(\dfrac{8(8.314 J·K^{-1})(298 K)}{\pi(0.002016 kg)}\right)} = 1770 \dfrac{m}{s} \)

\[ Z_{H_2,H_2}=\dfrac{(2.30 x 10^{-19}m^2)(1770 \dfrac{m}{s})(2.43 x 10^{25} m^{-3})^2}{\sqrt{2}} = 1.7 x 10^{35} s^{-1}m^{-3} = 1.7 x 10^{29} s^{-1}cm^{-3} \nonumber \]