31.1: La Célula Unitaria es el Bloque de Construcción Fundamental de un Cristal

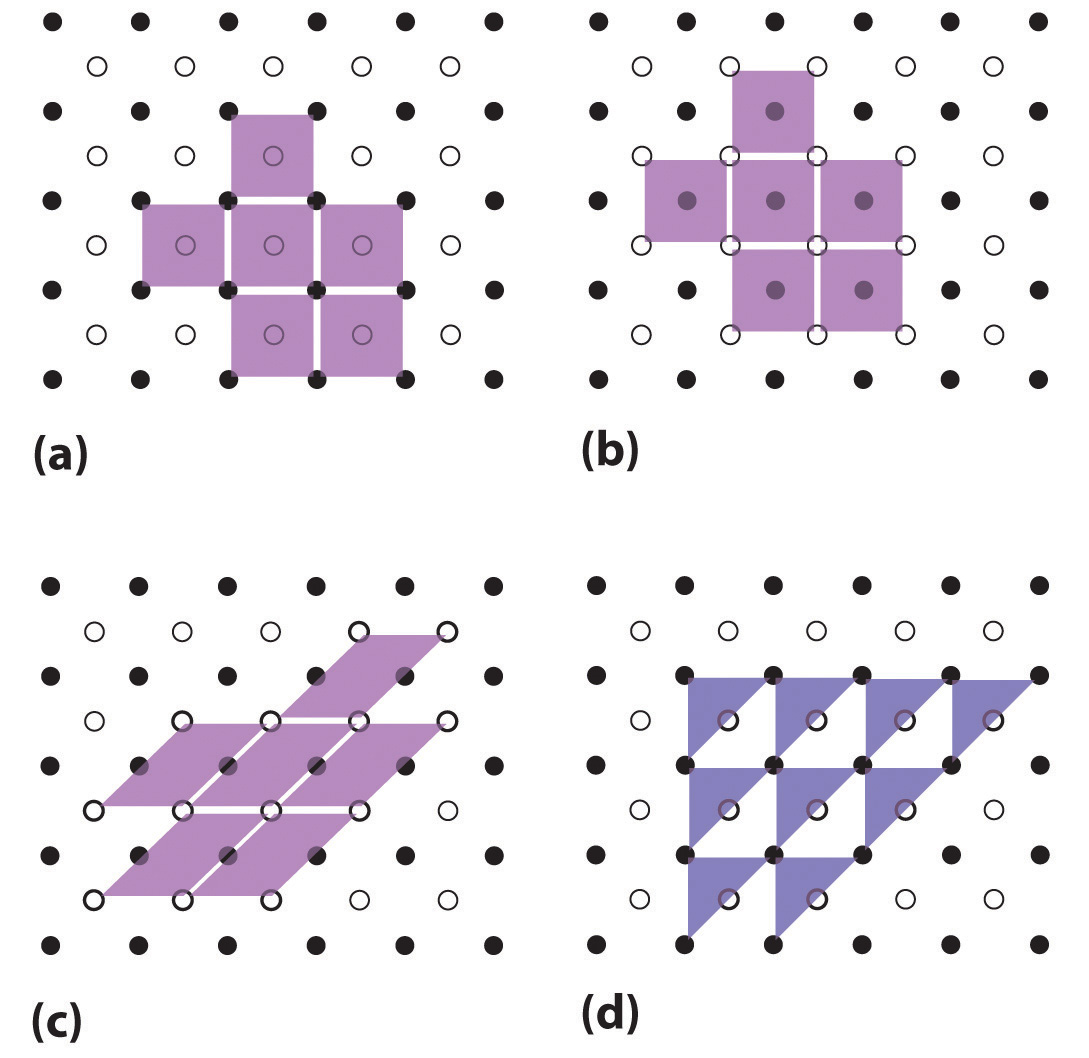
La disposición tridimensional regular de átomos o iones en un cristal generalmente se describe en términos de una red espacial y una celda unitaria. Para ver qué significan estos dos términos, consideremos primero los patrones bidimensionales que se muestran en la Figura \(\PageIndex{1}\). Podemos pensar en cada una de estas tres estructuras como un gran número de repeticiones en dos direcciones. Cada paralelogramo púrpura claro representa una celda unitaria. Se muestran tres celdas unitarias válidas y una celda unitaria no válida para el patrón de puntos claros y oscuros.

Figura\(\PageIndex{1}\): Celdas unitarias en dos dimensiones. (a—c) Tres celosías bidimensionales ilustran las posibles elecciones de la celda unitaria. Las celdas unitarias difieren en sus ubicaciones u orientaciones relativas dentro de la celosía, pero todas son opciones válidas porque repetirlas en cualquier dirección llena el patrón general de puntos. (d) El triángulo no es una celda unitaria válida porque repetirlo en el espacio llena solo la mitad del espacio en el patrón. (CC BY-NC-SA; anónimo)

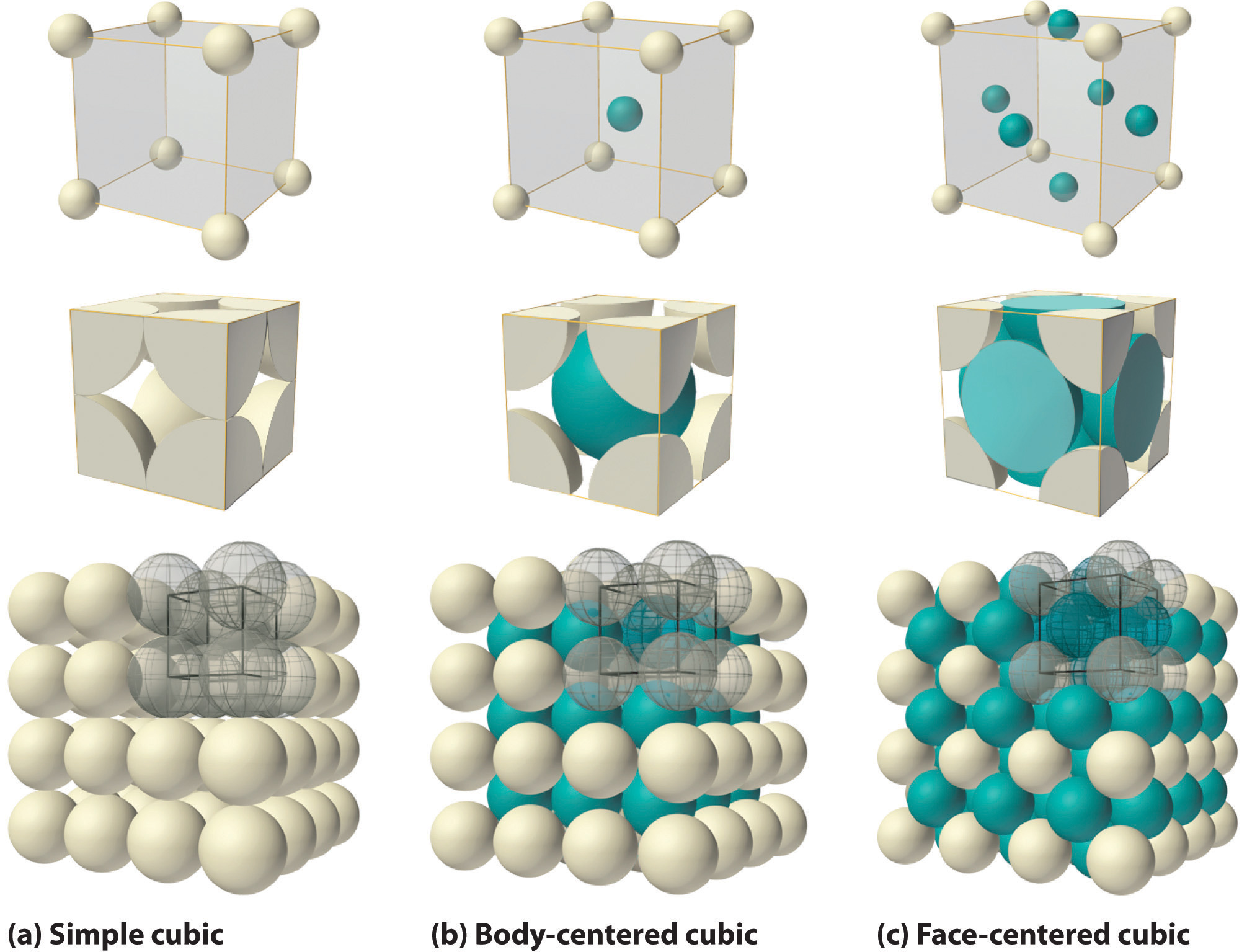
Encontrar la celda unitaria en una estructura cristalina tridimensional puede ser un desafío. La figura\(\PageIndex{2}\) muestra tres representaciones de una clase de estructuras tridimensionales: los tres tipos de celdas unitarias cúbicas. Las líneas negras y las esferas grises en la esquina superior derecha de las imágenes inferiores muestran una celda unitaria dentro de una colección más grande de celdas unitarias.

Figura\(\PageIndex{2}\): Los Tres Tipos de Celda Unitaria Cúbica. Para los tres tipos de celdas unitarias cúbicas, cúbicas simples (a), cúbicas centradas en el cuerpo (b) y cúbicas centradas en la cara (c), hay tres representaciones para cada una: un modelo de bola y palo, un modelo de corte de relleno de espacio que muestra la porción de cada átomo que se encuentra dentro de la celda unitaria, y un agregado de varias unidades celdas. (CC BY-NC-SA; anónimo)

La figura \(\PageIndex{3}\)ilustra la celosía espacial y la celda unitaria para una estructura cristalina tridimensional real, la del cloruro de sodio.

Figura\(\PageIndex{3}\): (izquierda) La red cristalina y celda unitaria de un cristal de cloruro de sodio. Estructura del cristal de cloruro de sodio. Los iones de sodio y cloruro están alrededor en una estructura cúbica centrada en la cara (FCC). Los iones sodio, Na ⁺, se muestran en rojo. Los iones cloruro, Cl ^—, se muestran en verde. (derecha) La imagen macroscópica de la derecha muestra cubos de sal, los cuales demuestran la celda unitaria cúbica de NaCl (No siempre resulta de esta manera. Debido a que el crecimiento de los cristales es un proceso complejo, no se garantiza que la estructura cristalina macroscópica coincida con la celda unitaria). (CC BY; OpenStax)

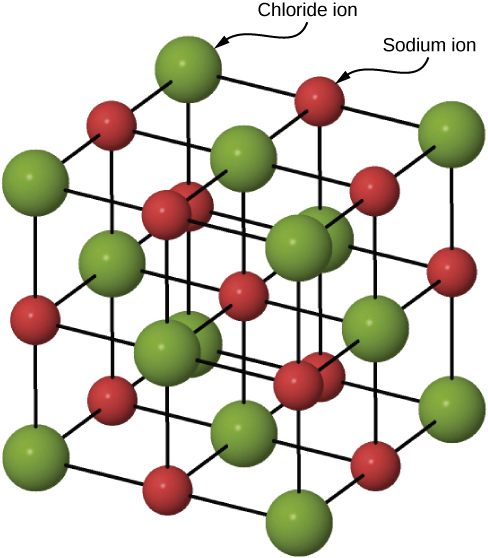
Una celda unitaria para esta estructura es un cubo cuyas esquinas están todas ocupadas por iones de sodio. Alternativamente, la celda unitaria podría elegirse con iones cloruro en las esquinas. La celda unitaria de cloruro de sodio contiene cuatro iones de sodio y cuatro iones de cloruro. Al llegar a tal respuesta debemos tener en cuenta que muchos de los iones son compartidos por varias células adyacentes (la parte c de la Figura \(\PageIndex{2}\)muestra este pozo). Específicamente, los iones de sodio en los centros de las caras cuadradas de la célula son compartidos por dos células, de manera que solo la mitad de cada una se encuentra dentro de la celda unitaria. Dado que hay seis caras a un cubo, esto hace un total de tres iones de sodio. En el centro de cada borde de la celda unitaria hay un ion cloruro que es compartido por cuatro celdas adyacentes y así cuenta un cuarto. Dado que hay doce bordes, esto hace que tres iones cloruro. En cada rincón del cubo, un ión de sodio es compartido por otras ocho células. Dado que hay ocho llegadas, esto suma a un ion sodio más. Por último, hay un ion cloruro en el cuerpo del cubo no compartido por ninguna otra célula. El total general es de cuatro iones de sodio y cuatro iones de cloruro.

Una fórmula general puede derivarse de los argumentos que se acaban de presentar para contar N, el número de átomos o iones en una celda unitaria. Es

\[N=N_{\text{body}}\text{ + }\frac{N_{\text{face}}}{\text{2}}\text{ + }\frac{N_{\text{edge}}}{\text{4}}\text{ + }\frac{N_{\text{corner}}}{\text{8}}\nonumber \]

Sistemas de Cristal

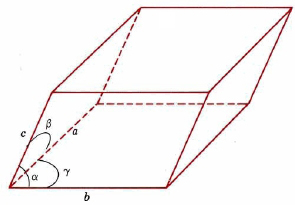
Las celdas unitarias no necesitan ser cubos, sino que deben ser figuras tridimensionales de lados paralelos. Un ejemplo general se muestra en la Figura\(\PageIndex{4}\). Tal celda puede describirse en términos de las longitudes de tres bordes adyacentes, a, b y c, y los ángulos entre ellos, α, β y γ.

Figura\(\PageIndex{4}\) Una celda unitaria generalizada con lados a, b y c, y ángulos α, β y γ.

Los cristales suelen clasificarse como pertenecientes a una de las catorce celosías de Bravais, dependiendo de la forma de la celda unitaria y del número de átomos en la celda unitaria. Estos catorce sistemas se muestran en la Figura\(\PageIndex{5}\) a continuación. La figura\(\PageIndex{6}\) enumera los detalles sobre cada uno de los sistemas de celosía.

Figura\(\PageIndex{5}\): Los siete sistemas de celosía y catorce celosías de Bravais. (Colaboradores de Wikipedia. (2021, 2 de septiembre). Celosía Bravais. En Wikipedia, La enciclopedia libre. Recuperado 01:22, 3 de octubre de 2021, de https://en.Wikipedia.org/w/index.php?title=Bravais_lattice&oldid=1042012012)

Figura\(\PageIndex{6}\): Los seis parámetros de celosía son las tres distancias axiales (\(a, b, \text{and} \, c\)) y los tres ángulos axiales (\(\alpha,, \beta, \text{and} \, \gamma\)). (Colaboradores de Wikipedia. (2021, 2 de septiembre). Celosía Bravais. En Wikipedia, La enciclopedia libre. Recuperado 01:22, 3 de octubre de 2021, de https://en.Wikipedia.org/w/index.php?title=Bravais_lattice&oldid=1042012012)

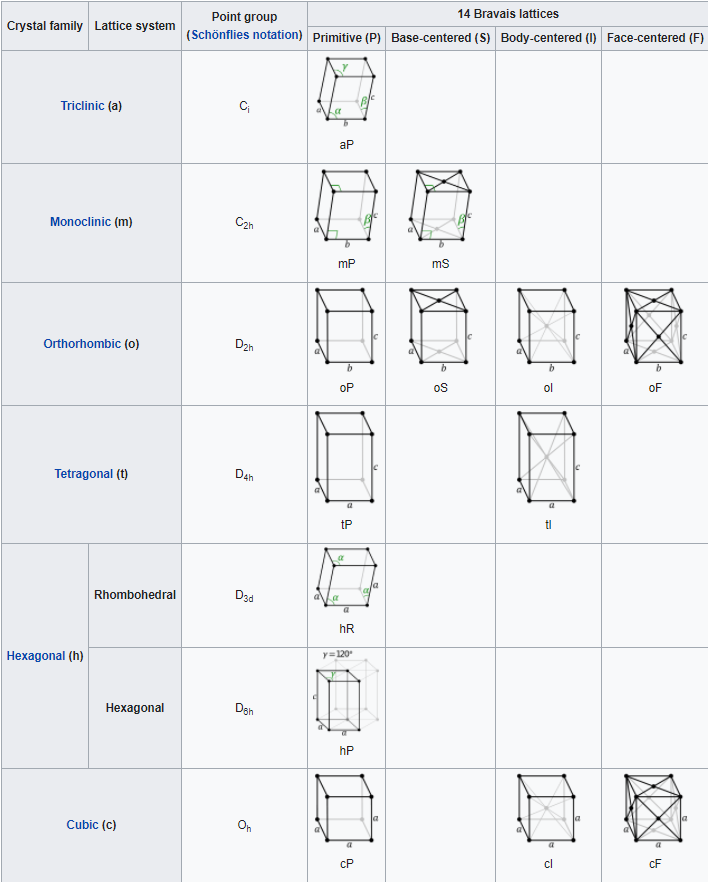
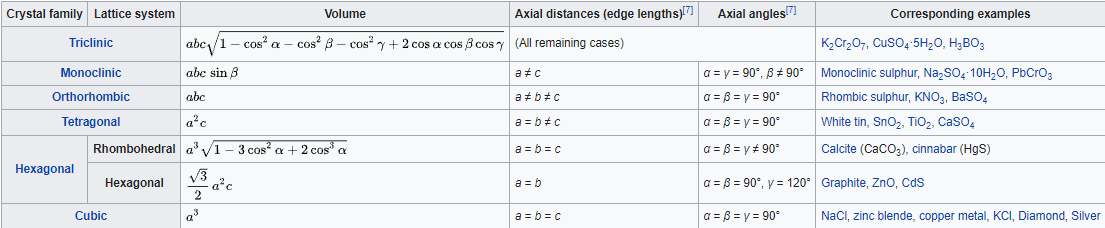
El sistema de celosía más simple es el sistema cúbico, en el que todos los bordes de la celda unitaria son iguales y todos los ángulos son de 90°. Los sistemas tetragonal y ortorrómbico también cuentan con celdas rectangulares, pero los bordes no son todos iguales. En los sistemas restantes, algunos o todos los ángulos no son de 90°. El menos simétrico es el triclínico, en el que no hay bordes iguales y ningún ángulo es igual entre sí ni a 90°.

Sistemas Close-Packed

Una clase importante de estructuras cristalinas se encuentra en muchos metales y también en los gases nobles solidificados donde los átomos (que son todos iguales) se empaquetan lo más cerca posible. La mayoría de nosotros estamos familiarizados con el proceso de empaquetar esferas juntas, ya sea de jugar con canicas o BB de niños o de intentar apilar naranjas u otra fruta redonda en una pirámide. Sobre una superficie nivelada podemos disponer fácilmente una colección de esferas del mismo tamaño en una capa hexagonal muy compacta en la que cada esfera está tocando a seis de sus compañeros, como se ve Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\): Las esferas se pueden empaquetar estrechamente juntas en forma hexagonal, por lo que cada esfera está siendo tocada por otras 6 esferas en el mismo nivel. Esta es una estructura más empaquetada.

Entonces podemos agregar una segunda capa para que cada esfera agregada se acurruque en una depresión entre tres esferas en la capa de abajo. Dentro de esta segunda capa cada esfera también entra en contacto con seis vecinos, y la capa es idéntica a la primera. Parece que podemos agregar capa tras capa indefinidamente, o hasta que nos quedemos sin esferas. Cada esfera estará tocando a doce de sus compañeros ya que está rodeada por seis en el mismo plano y se anida entre tres en el plano de arriba y tres en el plano de abajo. Decimos que cada esfera tiene un número de coordinación de 12. Es imposible hacer cualquier otra estructura con un número de coordinación mayor, es decir, empacar más esferas dentro de un volumen dado. Por consiguiente, la estructura que se acaba de describir se denomina a menudo una estructura empaquetada.

Resulta que hay dos formas de crear una estructura muy compacta. Estas dos formas se muestran en la Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\). Una estructura más empaquetada se puede formar de dos maneras. La parte a muestra el empaque donde se utilizan dos tipos de capas diferentes. La parte b muestra empaque con 3 capas distintas.

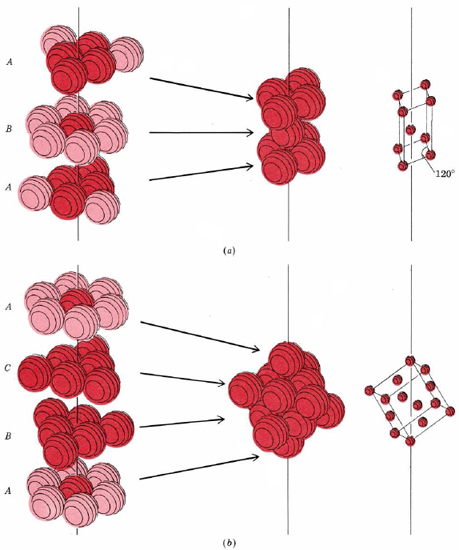
En la parte a de\(\PageIndex{8}\) la Figura la primera capa de esferas ha sido etiquetada A y la segunda etiquetada B para indicar que las esferas en la segunda capa no están directamente por encima de las de la primera. La tercera capa se encuentra directamente por encima de la primera, y por lo tanto está etiquetada como A. Si seguimos en la manera mostrada, agregando alternativamente A, luego B, luego A capas, obtenemos una estructura cuya celda unitaria (mostrada en la parte a) tiene dos lados iguales con un ángulo de 120° entre ellos. Otros ángulos son de 90°, por lo que la celda pertenece al sistema de cristales hexagonales. De ahí que esta estructura se llame hexagonal close packed (hcp).

En la parte b de\(\PageIndex{8}\) la Figura la primera capa de esferas ha sido etiquetada A y la segunda etiquetada B para indicar que las esferas en la segunda capa no están directamente por encima de las de la primera. En este sistema de empaque, la tercera capa está etiquetada como C porque no está directamente por encima de la primera o la segunda capa; tiene su propia orientación única. Si continuamos en la manera mostrada, agregando alternativamente A, luego B, luego capas C, obtenemos una estructura cuya celda unitaria (mostrada en la parte b) que tiene tres lados iguales con todos los ángulos a 90°, y así la celda pertenece al sistema de cristal cúbico. De ahí que esta estructura se llame cúbico cerrado empaquetado (ccp). Para repetir, tanto en las estructuras hexagonales compactas como en las cúbicas compactas, cada esfera tiene 12 vecinos más cercanos.

Figura\(\PageIndex{9}\). La parte a muestra la celda unitaria para la celosía cúbica cúbica empaquetada o centrada en la cara. La parte b muestra la celda unitaria para la red cúbica centrada en el cuerpo.

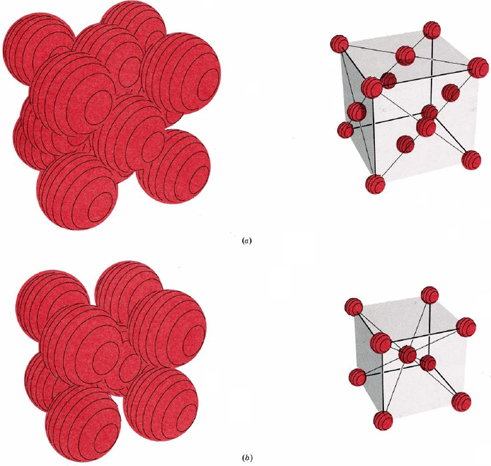
La figura\(\PageIndex{9}\) muestra dos tipos de celosías cúbicas, la cúbica centrada en la cara y la cúbica centrada en el cuerpo La celda unitaria de un cristal cúbico centrado en el cuerpo (bcc) es similar a la estructura fcc excepto que, en lugar de esferas en las caras, hay una sola esfera en el centro del cubo. Esta esfera central está rodeada por ocho vecinos en las esquinas de la celda unitaria, dando un número de coordinación de 8. Por lo tanto, la estructura de bcc no está tan compacta como las estructuras compactas que tenían un número de coordinación 12.

Ejemplo\(\PageIndex{1}\): Unit Cells

Cuente el número de esferas en la celda unitaria de (a) una estructura cúbica centrada en la cara y (b) una estructura cúbica centrada en el cuerpo.

Solución

Haciendo referencia a la Figura\(\PageIndex{9}\) y usando la ecuación:

\[N=N_{\text{body}}\text{ + }\frac{N_{\text{face}}}{\text{2}}\text{ + }\frac{N_{\text{edge}}}{\text{4}}\text{ + }\frac{N_{\text{corner}}}{\text{8}} \nonumber \]

encontramos

a)\[N=N_{\text{body}}\text{ + }\frac{N_{\text{face}}}{\text{2}}\text{ + }\frac{N_{\text{edge}}}{\text{4}}\text{ + }\frac{N_{\text{corner}}}{\text{8}}=\text{0 + }\frac{\text{6}}{\text{2}}\text{ + 0 + }\frac{\text{8}}{\text{8}}=\text{4} \nonumber \]

b)\[N=\text{1 + 0 + 0 + }\frac{\text{8}}{\text{8}}=\text{2} \nonumber \]

Ejemplo\(\PageIndex{2}\): Crystal Forms

El silicio tiene la misma estructura cristalina que el diamante. Ahora hay técnicas disponibles para el cultivo de cristales de este elemento que son prácticamente impecables. El análisis de algunos de estos cristales perfectos encontró que el lado de la celda unitaria tenía 543.102064pm de largo. La celda unitaria es un cubo que contiene ocho átomos de Si, pero es solo una de las celdas cúbicas simples ya discutidas. A partir de la composición isotópica, masa molar y densidad de los cristales, se determinó que un mol de Si en esta forma cristalina tiene un volumen de 12.0588349×10 ^-6 m ³. Determine N _A partir de estos datos.

Solución _{Este problema utiliza el conocimiento de la estructura cristalina de silicio para determinar N A.} A partir de la longitud del borde, podemos obtener el volumen de la celda unitaria cúbica. Sabemos que la unidad contiene ocho átomos, y como conocemos el volumen de un mol, podemos calcular N _A, con la constante Avogadro definida como el número de partículas por unidad de cantidad de sustancia.

\[N_{A}= \frac{N*V_{\text{m}}}{V_{\text{unit cell}}}=\frac{8\times{12.0588349}\times{10}^{-6}\text{m}^{3}}{({ 543.102064}\times{10}^{-12}\text{m})^{3}}={6.02214179}\times{10}^{23} \nonumber \]

Los valores utilizados para determinar este valor fueron tomados de cristales usando Densidad de Cristal de Rayos X (XRCD), para determinar la longitud lateral. Estos valores fueron utilizados en el análisis más reciente publicado por el Comité de Datos para la Ciencia y la Tecnología (CODATA) ^[1], que estandariza definiciones de constantes y unidades científicas importantes. El valor que acabas de calcular es, por lo tanto, la determinación más precisa de la constante de Avogadro a partir de 2007.

Es importante señalar que las esferas en estos modelos pueden representar átomos, iones monoatómicos, iones poliatómicos, moléculas, o una colección de moléculas.

1. ↑ Mohr, P.J., Taylor, B.N., y D. B. Newell. “CODATA Valores Recomendados de las Constantes Físicas Fundamentales: FCKLR2006.” Instituto Nacional de Estándares y Tecnología. 28 de diciembre de 2007. http://physics.nist.gov/cuu/Constants/codata.pdf

Ejemplo\(\PageIndex{1}\)

El cobre tiene una densidad de 8.930\(\dfrac{grams}{cm^3}\) a 20°C y la masa molar del cobre es 63.55\(\dfrac{grams}{mole}\). El cobre cristaliza como una celosía cúbica centrada en la cara. Calcular el radio cristalográfico de un átomo de cobre.

Solución

Al observar la figura\(\PageIndex{2}\) c, se puede determinar que hay 4 átomos por celda unitaria. Así, la masa de una celda unitaria es

\[\dfrac{(63.55 \, grams/mole)(4 \, atoms/cell)}{6.022 x 10^{23} \, atoms/mole} = 4.221 x 10^{-22} \, grams/cell \nonumber \]

El volumen de la celda unitaria es

\[V_{cell} = \dfrac{4.221 x 10^{-22} \, grams/cell}{8.930 \, grams/cm^3} = 4.727 x 10^{-23} \, cm^3\nonumber \]

La celda unitaria es cúbica, por lo tanto, todos los lados tienen la misma longitud, y\(V_{cell} = a^3\)

\[a = V_{cell}^{1/3} = 3.616 x 10^{-8} cm = 361.6 \, pm\nonumber \]

Como se muestra en la figura\(\PageIndex{2}\) c, la diagonal a través de la cara de la celda unitaria tiene una longitud de 4 veces el radio de un átomo de cobre. Así, la longitudh de la diagonal de la cara es\(\sqrt{2}a\), que equivale a\(\sqrt{2}(361.6 \, \text{pm})\) = 511.4 pm. Un cuarto de 511.4 pm es 127.8 pm.

Colaboradores y Atribuciones

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.

• Tom Neils (Grand Rapids Community College)