31.2: La orientación de un plano de celosía es descrita por sus índices Miller

La orientación de una superficie o un plano cristalino puede definirse considerando cómo el plano (o de hecho cualquier plano paralelo) intersecta los ejes cristalográficos principales del sólido. La aplicación de un conjunto de reglas conduce a la asignación de los índices Miller (hkl), que son un conjunto de números que cuantifican las intercepciones y así pueden ser utilizados para identificar de manera única el plano o superficie.

Asignación de índices Miller para un sistema de cristal cúbico

El siguiente tratamiento del procedimiento utilizado para asignar los índices Miller es uno simplificado (puede ser mejor si simplemente lo considera como una “receta”) y solo se considerará un sistema de cristal cúbico (uno que tenga una celda unitaria cúbica con dimensiones a x a x a) .

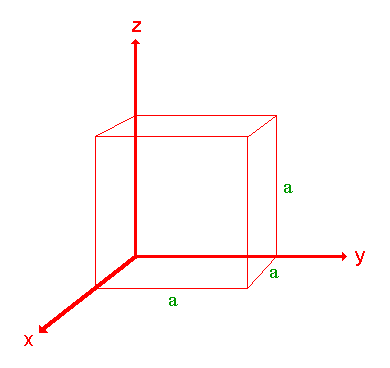
El procedimiento se ilustra más fácilmente usando un ejemplo por lo que primero consideraremos la siguiente superficie/plano:

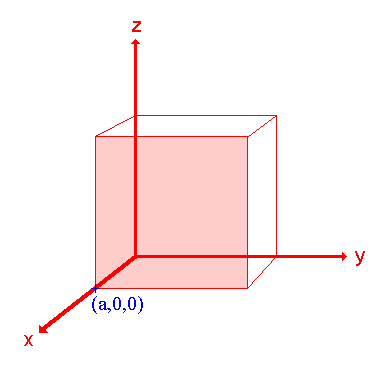
Paso 1: Identificar las intercepciones en los ejes x, y y z.

En este caso la intercepción en el eje x está en x = a (en el punto (a ,0,0)), pero la superficie es paralela a los ejes y - y z - estrictamente por lo tanto no hay intercepción en estos dos ejes pero consideraremos que la intercepción está en el infinito ( ∞) para el caso especial donde el plano es paralelo a un eje. Las intercepciones en los ejes x -, y - y z son así

Intercepciones: a, ∞, ∞

Paso 2: Especificar las intercepciones en coordenadas fraccionarias

Las coordenadas se convierten en coordenadas fraccionarias dividiendo por la dimensión celular respectiva; por ejemplo, un punto (x, y, z) en una celda unitaria de dimensiones a x b x c tiene coordenadas fraccionarias de (x/a , y/b, z/c). En el caso de una celda unitaria cúbica, cada coordenada simplemente se dividirá por la constante de celda cúbica, a. Esto da

Intercepciones fraccionarias: a/a, ∞/a, ∞/a es decir , 1, ∞, ∞

Paso 3: Toma los recíprocos de las intercepciones fraccionarias

Esta manipulación final genera los índices Miller que (por convención) deberían especificarse entonces sin estar separados por comas u otros símbolos. Los índices Miller también están encerrados entre corchetes estándar (...) cuando se está especificando una superficie única como la que se considera aquí.

Los recíprocos de 1 y ∞ son 1 y 0 respectivamente, cediendo así

Índices Miller: (100)

Entonces la superficie/plano ilustrado es el plano (100) del cristal cúbico.

Otros Ejemplos

1. La superficie (110)

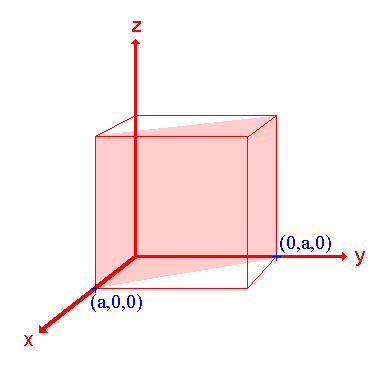Asignación Intercepciones: a, a, ∞ Intercepciones fraccionarias: 1, 1, ∞ Índices Miller: (110)

2. La superficie (111)

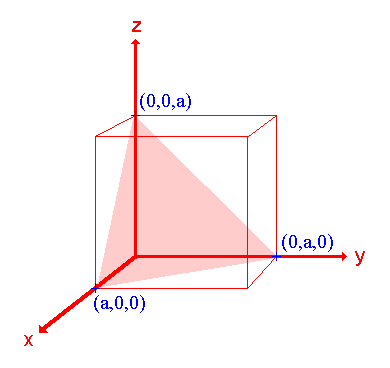Asignación Intercepciones: a, a, a Intercepciones fraccionarias: 1, 1, 1 Índices Miller: (111)

Las superficies (100), (110) y (111) consideradas anteriormente son las llamadas superficies de índice bajo de un sistema de cristal cúbico (la “baja” se refiere a que los índices Miller son números pequeños - 0 o 1 en este caso). Estas superficies tienen una importancia particular pero hay un número infinito de otros planos que pueden definirse usando la notación de índice Miller. Basta con mirar una más...

3. La superficie (210)

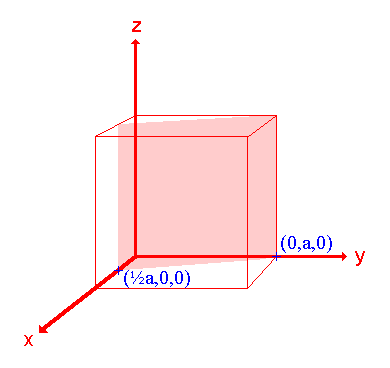Asignación Intercepciones: ½ a, a, ∞ Intercepciones fraccionarias: ½, 1, ∞ Índices Miller: (210)

Notas adicionales:

1. en algunos casos los índices Miller se multiplican o dividen mejor por un número común para simplificarlos, por ejemplo, eliminando un factor común. Esta operación de multiplicación simplemente genera un plano paralelo que se encuentra a una distancia diferente del origen de la celda unitaria particular que se está considerando. e.g. (200) se transforma a (100) dividiendo por 2.
2. si alguna de las intercepciones se encuentra en valores negativos en los ejes, entonces el signo negativo pasará a los índices de Miller; en tales casos el signo negativo se denota realmente sobregolpeando el número relevante. e.g. (00 -1) en cambio se denota por (\(00\bar{1}\)).
3. en el sistema de cristal hcp hay cuatro ejes principales; esto lleva a cuatro índices Miller, por ejemplo, puede ver artículos que hacen referencia a una superficie hcp (0001). Cabe señalar, sin embargo, que las intercepciones en los tres primeros ejes están necesariamente relacionadas y no completamente independientes; en consecuencia, los valores de los tres primeros índices de Miller también están vinculados por una simple relación matemática.

¿Qué son las superficies equivalentes a simetría?

En el siguiente diagrama las tres superficies resaltadas están relacionadas por los elementos de simetría del cristal cúbico, son totalmente equivalentes.

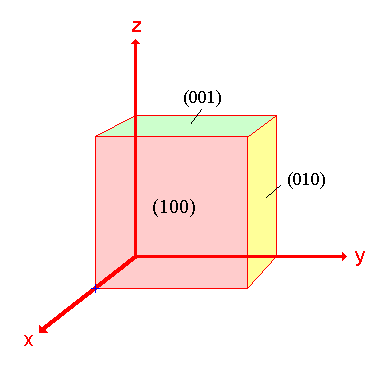
De hecho, hay un total de 6 caras relacionadas por los elementos de simetría y equivalentes a la (100) superficie - cualquier superficie perteneciente a este conjunto de superficies relacionadas con la simetría puede ser denotada por la notación más general {100} donde los índices de Miller de una de las superficies están encerrados en corchetes rizados.

Nota importante final: en el sistema cúbico el plano (hkl) y el vector [hkl], definidos de manera normal con respecto al origen, son normales entre sí pero esta característica es única para el sistema de cristales cúbicos y no aplica a sistemas cristalinos de menor simetría.

La distancia perpendicular entre planos

El símbolo\(d\) se utiliza para designar el espaciado perpendicular entre planos adyacentes. En el cuadro se\(\PageIndex{1}\) muestran las ecuaciones para calcular el valor de d para cuatro de los siete sistemas cristalinos.

Tabla\(\PageIndex{1}\): Ecuaciones para calcular el espaciamiento entre planos adyacentes,\(d\)

Sistema	Ecuación para\(d\)
cúbico	\ (d\) ">\(\dfrac{1}{d^2} = \dfrac{h^2+k^2+l^2}{a^2}\)
tetragonal	\ (d\) ">\(\dfrac{1}{d^2} = \dfrac{h^2+k^2}{a^2}+\dfrac{l^2}{c^2}\)
hexagonal	\ (d\) ">\(\dfrac{1}{d^2} = \dfrac{4}{3}\left(\dfrac{h^2+hk+k^2}{a^2} \right) +\dfrac{l^2}{c^2}\)
ortorrómbico	\ (d\) ">\(\dfrac{1}{d^2} = \dfrac{h^2}{a^2}+\dfrac{k^2}{b^2} +\dfrac{l^2}{c^2}\)

Ejemplo\(\PageIndex{1}\)

Si una celda unitaria tetragonal tiene dimensiones\(a\) =\(b\) = 501pm y\(c\) = 451pm, calcule la distancia perpendicular entre los 111 planos.

Solución

Para una celda unitaria tetragonal

\[\dfrac{1}{d^2} = \dfrac{h^2+k^2}{a^2}+\dfrac{l^2}{c^2}. \nonumber \]

Por lo tanto,

\[\begin{align*} \dfrac{1}{d^2} &= \dfrac{1+1}{(501 \, \text{pm})^2}+\dfrac{1}{(451 \, \text{pm})^2} \\[4pt] &= 1.29 \times 10^{-5} \, \text{pm}^{-2}. \end{align*} \nonumber \]

Entonces\(d = 279 \, \text{pm}\)

Colaboradores y Atribuciones

• Roger Nix (Queen Mary, University of London)

• Tom Neils (Grand Rapids Community College)