31.3: La separación entre planos de celosía puede determinarse a partir de mediciones de difracción de rayos X

La cristalografía de rayos X es una técnica instrumental utilizada para determinar la disposición de los átomos de un sólido cristalino en el espacio tridimensional. Esta técnica aprovecha el espaciamiento interatómico de la mayoría de los sólidos cristalinos al emplearlos como rejilla de difracción para luz de rayos X, que tiene longitudes de onda del orden de 1 angstrom (10 ^-8 cm).

Introducción

En 1895, Wilhelm Rontgen descubrió rayos x. La naturaleza de los rayos x, ya fueran partículas o radiación electromagnética, fue tema de debate hasta 1912. Si la idea de onda era correcta, los investigadores sabían que la longitud de onda de esta luz tendría que ser del orden de 1 Angstrom (Å) (10 ^-8 cm). La difracción y medición de longitudes de onda tan pequeñas requerirían una rejilla con espaciamiento en el mismo orden de magnitud que la luz.

En 1912, Max von Laue, de la Universidad de Munich en Alemania, postuló que los átomos en una red cristalina tenían una estructura regular y periódica con distancias interatómicas del orden de 1 Å. Sin tener ninguna evidencia que respalde su afirmación sobre las disposiciones periódicas de los átomos en una red, postuló además que la estructura cristalina podría ser utilizada para difractar rayos X, al igual que una rejilla en un espectrómetro infrarrojo puede difractar la luz infrarroja. Su postulado se basó en los siguientes supuestos: la red atómica de un cristal es periódica, los rayos x son radiación electromagnética y la distancia interatómica de un cristal es del mismo orden de magnitud que la luz de rayos X. Las predicciones de Laue se confirmaron cuando dos investigadores: Friedrich y Knipping, fotografiaron con éxito el patrón de difracción asociado a la radiación de rayos X de cristalino\(CuSO_4 \cdot 5H_2O\). Nació la ciencia de la cristalografía de rayos X.

La disposición de los átomos necesita estar en una estructura ordenada y periódica para que difracten los haces de rayos X. Luego se utiliza un conjunto de cálculos matemáticos para producir un patrón de difracción que es característico de la disposición particular de los átomos en ese cristal. La cristalografía de rayos X sigue siendo hasta el día de hoy la principal herramienta utilizada por los investigadores para caracterizar la estructura y unión de muchos compuestos.

Difracción

La difracción es un fenómeno que ocurre cuando la luz se encuentra con un obstáculo. Las ondas de luz pueden doblarse alrededor del obstáculo o, en el caso de una hendidura, pueden viajar a través de las hendiduras. El patrón de difracción resultante mostrará áreas de interferencia constructiva, donde dos ondas interactúan en fase, e interferencia destructiva, donde dos ondas interactúan fuera de fase. El cálculo de la diferencia de fase se puede explicar examinando la Figura\(\PageIndex{1}\) a continuación.

Figura\(\PageIndex{1}\): Esta figura muestra la relación angular de los rayos X dispersos por partículas que se encuentran a lo largo del eje a en un sólido cristalino. Los rayos entrantes ingresan al cristal en un ángulo de\(\alpha_0 \), el ángulo de incidencia, y se dispersan desde los puntos de celosía en un ángulo de\(\alpha\). (CC BY-NC; Ümit Kaya vía LibreTexts)

En la figura anterior, dos ondas paralelas están golpeando una rejilla en ángulo\(\alpha_o\). La ola incidente de la derecha viaja más lejos que la de la izquierda por una distancia de BD antes de llegar a la rejilla. La onda dispersa representada debajo del gradiente de la izquierda, viaja más lejos que la onda dispersa a la derecha por una distancia de CA. Entonces la diferencia de trayectoria total entre la onda izquierda y la onda derecha es AC - BD. Para observar una onda de alta intensidad (una creada a través de interferencia constructiva), la diferencia AC - BD debe ser igual a un número entero de longitudes de onda a observar en el ángulo\(\alpha\), AC - BD =\(n\lambda\), donde\(\lambda\) está la longitud de onda de la luz. Aplicando algunas propiedades trigonométricas básicas, se pueden mostrar las siguientes dos ecuaciones sobre las líneas:

\[BD = x \cos(\alpha_o) \nonumber \]

y

\[AC = x \cos (\alpha) \nonumber \]

donde\(x\) es la distancia entre los puntos donde se repite la difracción. Combinando las dos ecuaciones,

\[x(\cos \alpha - \cos \alpha_o) = n \lambda \nonumber \]

Método de Cristal Giratorio

Para describir la naturaleza periódica y tridimensional de los cristales, se emplean las ecuaciones de Laue:

\[ a(\cos \alpha – \cos \alpha_o) = nh\lambda \label{eq1} \]

\[b(\cos \beta – \cos \beta_o) = nk\lambda \label{eq2} \]

\[c(\cos \gamma – \cos \gamma_o) = nl\lambda \label{eq3} \]

donde\(a\)\(b\), y\(c\) son los tres ejes de la celda unitaria,\(\alpha_o\),\(\beta_o\),\(\gamma_o\) son los ángulos de radiación incidente, y\(\alpha\)\(\beta\), y\(\gamma\) son los ángulos de la radiación difractada. El\(n\) término se refiere al orden de las reflexiones. Si\(n\) = 1, entonces las reflexiones son reflexiones de primer orden. Si\(n\) = 2, entonces las reflexiones son reflexiones de segundo orden.

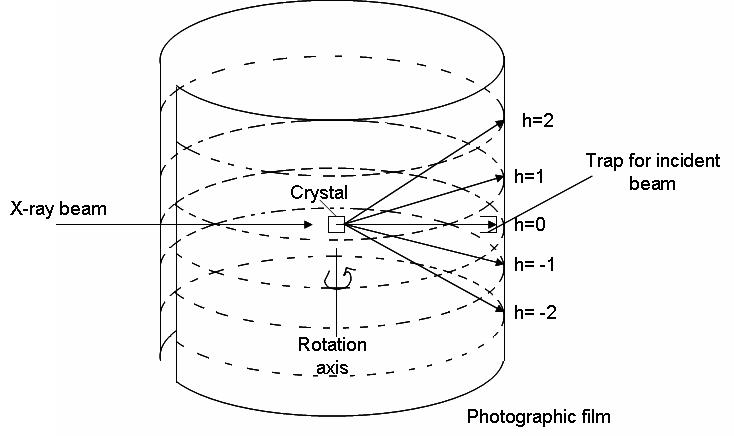
Una señal de difracción (interferencia constructiva) surgirá cuando\(h\)\(k\), y\(l\) son valores enteros. El método del cristal giratorio emplea estas ecuaciones. La radiación de rayos X se muestra sobre un cristal, rodeado por una película cilíndrica, a medida que gira alrededor de uno de sus ejes celulares unitarios. El haz golpea el cristal en un ángulo de 90 grados. Usando la ecuación 1 anterior, vemos que si\(\alpha_o\) es de 90 grados, entonces\(\cos \alpha_o = 0\). Para que la ecuación se mantenga verdadera, podemos establecer h=0, dado que\(\alpha\) = 90. Las tres ecuaciones anteriores serán satisfechas en diversos puntos a medida que el cristal gira. Esto da lugar a un patrón de difracción (mostrado en la figura\(\PageIndex{2}\) como múltiples valores de h). La película cilíndrica es luego desenvuelta y desarrollada.

La siguiente ecuación se puede utilizar para determinar la longitud del eje alrededor del cual se giró el cristal:

\[ a = \dfrac{nh \lambda}{\cos (\tan^{-1} (y/r))} \nonumber \]

donde a es la longitud del eje, y es la distancia desde\(h=0\) hasta el\(h\) de interés,\(r\) es el radio de la película (o la distancia desde el centro del cristal al detector), y\(\lambda\) es la longitud de onda de la radiación de rayos X utilizada.

Figura\(\PageIndex{2}\): El patrón de difracción de rayos X de los planos\(h\) 00 de un cristal montado de tal manera que los rayos X entrantes son perpendiculares al eje a del cristal.

Los difractómetros modernos utilizan detectores electrónicos de centelleo o detectores de área que actúan como una especie de “película” electrónica. Con estos detectores, los datos de difracción pueden enviarse directamente a una computadora y analizarse mucho más rápidamente que la película fotográfica. \(\PageIndex{3}\) shows a mounted crystal and its x-ray diffraction pattern.Ejemplo de Figura\(\PageIndex{1}\)

Figura\(\PageIndex{3}\): Arriba) Esta es una imagen de un cristal de proteína montado en un bucle (UC Davis Structural Biology Lab);

Abajo) Este es un patrón de difracción creado a partir del mutante APS Kinasa D63N del cristal anterior (UC Davis Structural Biology Lab)

Para un detector con una superficie plana, las reflexiones de un cristal cúbico primitivo golpearían la superficie en un patrón similar al que se muestra en la figura\(PageIndex{4}\)

Figura\(\PageIndex{1}\): Una porción del patrón de reflexión de algunos planos hkl de un cristal cúbico primitivo. El cristal está alineado de manera que el haz de rayos X entrante sea perpendicular al eje a. Esta misma disposición se utiliza para el cristal en el Ejemplo\(\PageIndex{1}\) a continuación. (CC BY-NC; Ümil Kaya vía LibreTexts)

Ejemplo\(\PageIndex{1}\)

Supongamos que desea medir la longitud de una celda unitaria\(a\) de un cristal que tiene celda unitaria cúbica primitiva. En la Figura se muestra un primer plano de la configuración experimental\(\PageIndex{4}\). El cristal está alineado de manera que los rayos X entrantes sean perpendiculares al eje a. La distancia entre el centro del cristal y la superficie del detector es de 5.50 cm. La distancia entre los puntos detectados dispersos por los 000 planos y los 100 planos es de 2.50 cm, y se dispersa en un ángulo de\(\alpha\). La longitud de onda de la luz de la fuente de rayos X de cobre es 154.4 pm. Determine la longitud de la celda unitaria a lo largo del eje a.

Figura\(\PageIndex{4}\): Una vista ampliada de rayos X sometidos a dispersión desde los 100 planos en un ángulo de\(\alpha\). (CC BY-NC; Ümit Kaya vía LibreTexts)

Solución

El ángulo\(\alpha\) puede ser determinado por el hecho de que\(\tan \alpha\) =\(\dfrac{5.50}{2.50}\). Así\(\tan ^{-1}(2.2)\), da\(\alpha\) = 65.56. Luego podemos encontrar la longitud de a de la ecuación 30.3.10

a =\(\dfrac{(1)(154.4 \, pm)}{\cos (65.56)} = 373.2 \, pm \)

Ley de Bragg aplicada a los cristales

Una segunda forma de analizar la difracción de rayos X es usar la ley de Bragg. La difracción de un haz de rayos X por sólidos cristalinos ocurre cuando la luz interactúa con la nube de electrones que rodea los átomos del sólido. Debido a la estructura cristalina periódica de un sólido, es posible describirlo como una serie de planos con una distancia interplanar igual. A medida que un haz de rayos X golpea la superficie del cristal en ángulo\(\theta\), parte de la luz se difractará en ese mismo ángulo alejándose del sólido (Figura\(\PageIndex{5}\)). El resto de la luz viajará al cristal y parte de esa luz interactuará con el segundo plano de átomos. Parte de la luz se difractará en ángulo\(theta\), y el resto viajará más profundamente en el sólido. Este proceso se repetirá para los muchos planos en el cristal. Los haces de rayos X recorren diferentes longitudes de trayectoria antes de chocar con los diversos planos del cristal, por lo que después de la difracción, los haces interactuarán constructivamente solo si la diferencia de longitud de trayectoria es igual a un número entero de longitudes de onda (al igual que en el caso de difracción normal anterior). En la siguiente figura, la diferencia en las longitudes de trayectoria del haz golpeando el primer plano y el haz que golpea el segundo plano es igual a BG + GF. Entonces, los dos haces difractados interferirán constructivamente (estarán en fase) solo si\(BG + GF = n \lambda\). La trigonometría básica nos dirá que los dos segmentos son iguales entre sí con la distancia interplanar multiplicada por el seno del ángulo\(\theta\). Entonces obtenemos:

\[ BG = BC = d \sin \theta \label{1} \]

Por lo tanto,

\[ 2d \sin \theta = n \lambda \label{2} \]

Esta ecuación es conocida como Ley de Bragg, que lleva el nombre de W. H. Bragg y su hijo, W. L. Bragg; quienes descubrieron esta relación geométrica en 1912. La Ley de Bragg relaciona la distancia entre dos planos en un cristal y el ángulo de reflexión con la longitud de onda de los rayos X. Los rayos X que se difractan del cristal tienen que estar en fase para poder ser observados. Solo se registrarán ciertos ángulos que cumplan la siguiente condición:

\[ \sin \theta = \dfrac{n \lambda}{2d} \label{3} \]

Por razones históricas, el espectro de difracción resultante se representa como intensidad vs\(2θ\).

Ejemplo\(\PageIndex{1}\)

El metal cesio tiene una estructura de cristal cúbico centrada en el cuerpo con una longitud de celda unitaria de 605.0 pm. Utilice la ecuación de Bragg para determinar los dos primeros ángulos de difracción observados desde los planos 110 cuando la longitud de onda de los rayos X es de 154.4 pm.

Solución

De la sección 31.2.3, encontramos que la distancia interplanar para celdas cúbicas se puede calcular usando la ecuación

\[\dfrac{1}{d^2} = \dfrac{h^2+k^2+l^2}{a^2} \nonumber \]

Si cuadramos la ecuación 31.3.10 obtenemos

\[ \sin^2 \theta = \dfrac{n^2 \lambda^2}{4d^2} \nonumber \]

Combinando estas dos ecuaciones, obtenemos

\[ \sin^2 \theta = \dfrac{n^2 \lambda^2}{4a^2}(h^2+k^2+l^2) \nonumber \]

El ángulo de difracción más pequeño ocurre cuando\(n = 1\)

\[ \sin^2 \theta = \dfrac{(1^2) (154.4 \ , pm)^2}{4(605.0)^2}(1^2+1^2+0^2) = 0.03257 \nonumber \]

Así,\(\theta\) = 10.40°

El siguiente ángulo de difracción más grande ocurre cuando\(n = 1\)

\[ \sin^2 \theta = \dfrac{(2^2) (154.4 \ , pm)^2}{4(605.0)^2}(1^2+1^2+0^2) = 0.1303 \nonumber \]

Así,\(\theta\) = 21.16°

En la siguiente sección, discutiremos los factores que determinan la fase y la amplitud de los múltiples rayos X dispersos producidos durante la difracción.

Referencias

1. Skoog, D. A.; Holler, F. J.; Stanley R. C.; Principios del Análisis Instrumental; Thomson Brooks/Cole: Belmont CA, 2007.
2. Sands, D. E.; Introducción a la Cristalografía; Dover Publications, Inc.; Nueva York, 1975
3. Drenth, Ene. Principios de Cristalografía de rayos X de Proteína, 3a edición. 2007, Springer Science + Business Media, LLC. pg. 14.
4. Rodas, Gale. Cristalografía Made Crystal Clear, 3a edición. 2006, Elsevier Inc. pg. 33, 55 - 57.
5. Experimentación real realizada con APS Kinasa D63N Penicillium Chrysogenum.

Colaboradores

• Roman Kazantsev (UC Davis) y Michelle Towles (UC Davis)
• Tom Neils - Colegio Comunitario de Grand Rapids