32.3: Vectores
- Page ID
- 79689
En este capítulo revisaremos algunos conceptos que probablemente conozcas de tus cursos de física. Este capítulo no pretende cubrir el tema de manera integral, sino que toca algunos conceptos que usarás en tus clases de química física.
Un vector es una cantidad que tiene tanto una magnitud como una dirección, y como tales se utilizan para especificar la posición, velocidad e impulso de una partícula, o para especificar una fuerza. Los vectores generalmente se denotan con símbolos en negritas (por ejemplo\(\mathbf{u}\)) o con una flecha encima del símbolo (por ejemplo\(\vec{u}\)). Una tilde colocada encima o debajo del nombre del vector también se usa comúnmente en taquigrafía (\(\widetilde{u}\),\(\underset{\sim}{u}\)).
Si multiplicamos un número\(a\) por un vector\(\mathbf{v}\), obtenemos un nuevo vector que es paralelo al original pero con una longitud que es\(a\) por la longitud de\(\mathbf{v}\). Si\(a\) es\(a\mathbf{v}\) puntos negativos en la dirección opuesta a\(\mathbf{v}\). Podemos expresar cualquier vector en términos de los llamados vectores unitarios. Estos vectores, que se designan\(\hat{\mathbf{i}}\),\(\hat{\mathbf{j}}\) y\(\hat{\mathbf{k}}\), tienen longitud unitaria y punto a lo largo del positivo\(x, y\) y\(z\) eje del sistema de coordenadas cartesianas (Figura\(\PageIndex{1}\)). El símbolo\(\hat{\mathbf{i}}\) se lee “i-hat”. Los sombreros se utilizan para denotar que un vector tiene longitud unitaria.
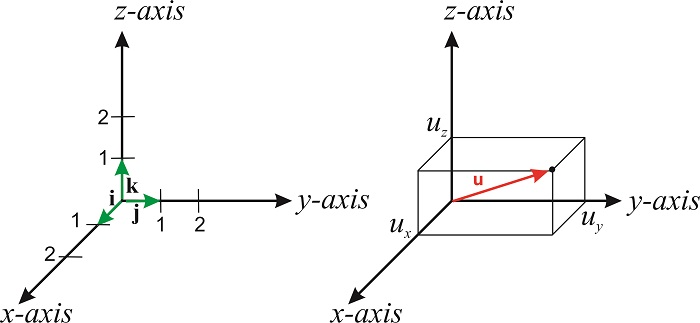
La longitud de\(\mathbf{u}\) es su magnitud (o módulo), y generalmente se denota por\(u\):
\[\label{eq:vectors1} u=|u|=(u_x^2+u_y^2+u_z^2)^{1/2}\]
Si tenemos dos vectores\(\mathbf{u}=u_x\hat{\mathbf{i}}+u_y \hat{\mathbf{j}}+u_z \hat{\mathbf{k}}\) y\(\mathbf{v}=v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}+v_z \hat{\mathbf{k}}\), podemos agregarlos para obtener
\[\mathbf{u}+\mathbf{v}=(u_x+v_x)\hat{\mathbf{i}}+(u_y+v_y)\hat{\mathbf{j}}+(u_z+v_z)\hat{\mathbf{k}} \nonumber\]
o restarlos para obtener:
\[\mathbf{u}-\mathbf{v}=(u_x-v_x)\hat{\mathbf{i}}+(u_y-v_y)\hat{\mathbf{j}}+(u_z-v_z)\hat{\mathbf{k}} \nonumber\]
Cuando se trata de multiplicar, podemos realizar el producto de dos vectores de dos maneras distintas. El primero, que da como resultado un escalar (un número), se denomina producto escalar o producto punto. El segundo, que da como resultado un vector, se llama el producto vector (o cruz). Ambas son operaciones importantes en la química física.
El producto escalar
El producto escalar de los vectores\(\mathbf{u}\) y\(\mathbf{v}\), también conocido como el producto punto o producto interno, se define como (observe el punto entre los símbolos que representan los vectores)
\[\mathbf{u}\cdot \mathbf{v}=|\mathbf{u}||\mathbf{v}|\cos \theta \nonumber\]
donde\(\theta\) está el ángulo entre los vectores. Observe que el producto punto es cero si los dos vectores son perpendiculares entre sí, y es igual al producto de sus valores absolutos si son paralelos. Es fácil demostrar que
\[\mathbf{u}\cdot \mathbf{v}=u_xv_x+u_yv_y+u_zv_z \nonumber\]
Ejemplo\(\PageIndex{1}\)
Mostrar que los vectores
\[ \begin{align*} \mathbf{u_1} &=\dfrac{1}{\sqrt{3}}\hat{\mathbf{i}}+\dfrac{1}{\sqrt{3}}\hat{\mathbf{j}}+\dfrac{1}{\sqrt{3}}\hat{\mathbf{k}} \\[4pt] \mathbf{u_2} &=\dfrac{1}{\sqrt{6}}\hat{\mathbf{i}}-\dfrac{2}{\sqrt{6}}\hat{\mathbf{j}}+\dfrac{1}{\sqrt{6}}\hat{\mathbf{k}} \\[4pt] \mathbf{u_3} &=-\dfrac{1}{\sqrt{2}}\hat{\mathbf{i}}+\dfrac{1}{\sqrt{2}}\hat{\mathbf{k}} \end{align*} \nonumber\]
son de longitud unitaria y son mutuamente perpendiculares.
Solución
La longitud de los vectores son:
\[ \begin{align*} |\mathbf{u_1}|&=\left[\left(\dfrac{1}{\sqrt{3}}\right)^2+\left(\dfrac{1}{\sqrt{3}}\right)^2+\left(\dfrac{1}{\sqrt{3}}\right)^2\right]^{1/2}=\left[\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}\right]^{1/2}=1 \\[4pt] |\mathbf{u_2}| &=\left[\left(\dfrac{1}{\sqrt{6}}\right)^2+\left(-\dfrac{2}{\sqrt{6}}\right)^2+\left(\dfrac{1}{\sqrt{6}}\right)^2\right]^{1/2}=\left[\dfrac{1}{6}+\dfrac{4}{6}+\dfrac{1}{6}\right]^{1/2}=1 \\[4pt] |\mathbf{u_3}| &=\left[\left(-\dfrac{1}{\sqrt{2}}\right)^2+\left(\dfrac{1}{\sqrt{2}}\right)^2\right]^{1/2}=\left[\dfrac{1}{2}+\dfrac{1}{2}\right]^{1/2}=1 \end{align*} \nonumber\]
Para probar si dos vectores son perpendiculares, realizamos el producto punto:
\[ \begin{align*} \mathbf{u_1}\cdot \mathbf{u_2}&=\left(\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{6}}-\dfrac{1}{\sqrt{3}}\dfrac{2}{\sqrt{6}}+\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{6}}\right)=0 \\[4pt] \mathbf{u_1}\cdot \mathbf{u_3} &=\left(-\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{2}}\right)=0 \\[4pt] \mathbf{u_2}\cdot \mathbf{u_3} &=\left(-\dfrac{1}{\sqrt{6}}\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{6}}\dfrac{1}{\sqrt{2}}\right)=0 \end{align*} \nonumber\]
Por lo tanto, acabamos de demostrar que los tres pares son mutuamente perpendiculares, y los tres vectores tienen longitud unitaria. En otras palabras, estos vectores son los vectores\(\hat{\mathbf{i}}\),\(\hat{\mathbf{j}}\) y\(\hat{\mathbf{k}}\) rotados en el espacio.
Si el producto punto de dos vectores (de cualquier dimensión) es cero, decimos que los dos vectores son ortogonales. Si los vectores tienen longitud unitaria, decimos que están normalizados. Si dos vectores están ambos normalizados y son ortogonales, decimos que son ortonormales. El conjunto de vectores mostrados en el ejemplo anterior forman un conjunto ortonormal. [vectors:ortonormal] Estos conceptos también se aplican a vectores que contienen entradas complejas, pero ¿cómo realizamos el producto punto en este caso?
En general, el cuadrado del módulo de un vector es
\[|\mathbf{u}|^2=\mathbf{u}\cdot \mathbf{u}=u_x^2+u_y^2+u_z^2. \nonumber\]
Sin embargo, esto no funciona correctamente para vectores complejos. El cuadrado de\(i\) es -1, lo que significa que corremos el riesgo de tener valores absolutos no positivos. Para abordar este problema, presentamos una versión más general del producto punto:
\[\mathbf{u}\cdot \mathbf{v}=u_x^*v_x+u_y^*v_y+u_z^*v_z, \nonumber\]
donde el “\(*\)” se refiere al conjugado complejo. Por lo tanto, para calcular el módulo de un vector\(\mathbf{u}\) que tiene entradas complejas, utilizamos su conjugado complejo:
\[|\mathbf{u}|^2=\mathbf{u}^*\cdot \mathbf{u} \nonumber\]
Ejemplo\(\PageIndex{2}\): Calculating the Modulus of a vector
Calcular el módulo del siguiente vector:
\[\mathbf{u}=\hat{\mathbf{i}}+i \hat{\mathbf{j}} \nonumber\]
Solución
\[|\mathbf{u}|^2=\mathbf{u}^*\cdot \mathbf{u}=(\hat{\mathbf{i}}-i \hat{\mathbf{j}})(\hat{\mathbf{i}}+i \hat{\mathbf{j}})=(1)(1)+(-i)(i)=2\rightarrow |\mathbf{u}|=\sqrt{2} \nonumber\]
Análogamente, si los vectores contienen entradas complejas, podemos probar si son ortogonales o no verificando el producto punto\(\mathbf{u}^*\cdot \mathbf{v}\).
Ejemplo\(\PageIndex{3}\): Confirming orthogonality
Determina si el siguiente par de vectores son ortogonales (¡no confundas el número irracional\(i\) con el vector unitario\(\hat{\mathbf{i}}\)!)
\[\mathbf{u}=\hat{\mathbf{i}}+(1-i)\hat{\mathbf{j}} \nonumber\]
y
\[\mathbf{v}=(1+i)\hat{\mathbf{i}}+\hat{\mathbf{j}} \nonumber\]
Solución
\[\mathbf{u}^*\cdot \mathbf{v}=(\hat{\mathbf{i}}+(1+i)\hat{\mathbf{j}})((1+i)\hat{\mathbf{i}}+\hat{\mathbf{j}})=(1)(1+i)+(1+i)(1)=2+2i\neq 0 \nonumber\]
Por lo tanto, los vectores no son ortogonales.
El producto vectorial
El producto vectorial de dos vectores es un vector definido como
\[\mathbf{u}\times \mathbf{v}=|\mathbf{u}| |\mathbf{v}| \mathbf{n} \sin\theta \nonumber\]
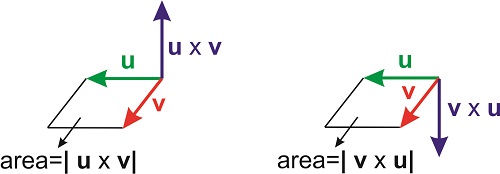
donde\(\theta\) está de nuevo el ángulo entre los dos vectores, y\(\mathbf{n}\) es el vector unitario perpendicular al plano formado por\(\mathbf{u}\) y\(\mathbf{v}\). La dirección del vector\(\mathbf{n}\) viene dada por la regla de la derecha. Extiende tu mano derecha y apunta tu dedo índice en la dirección de\(\mathbf{u}\) (el vector en el lado izquierdo del\(\times\) símbolo) y tu dedo índice en la dirección de\(\mathbf{v}\). La dirección de\(\mathbf{n}\), que determina la dirección de\(\mathbf{u}\times \mathbf{v}\), es la dirección de tu pulgar. Si quieres revertir la multiplicación, y realizar\(\mathbf{v}\times \mathbf{u}\), necesitas apuntar tu dedo índice en la dirección de\(\mathbf{v}\) y tu dedo índice en la dirección de\(\mathbf{u}\) (¡todavía usando la mano derecha!). El vector resultante apuntará en la dirección opuesta (Figura\(\PageIndex{1}\)).
La magnitud de\(\mathbf{u}\times \mathbf{v}\) es el producto de las magnitudes de los vectores individuales veces\(\sin \theta\). Esta magnitud tiene una interesante interpretación geométrica: es el área del paralelogramo formado por los dos vectores (Figura\(\PageIndex{1}\)).
El producto cruzado también se puede expresar como un determinante:
\[\mathbf{u}\times \mathbf{v}= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix} \nonumber\]
Ejemplo\(\PageIndex{1}\):
Dado\(\mathbf{u}=-2 \hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}\) y\(\mathbf{v}=3 \hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}\), calcular\(\mathbf{w}=\mathbf{u}\times \mathbf{v}\) y verificar que el resultado sea perpendicular a ambos\(\mathbf{u}\) y\(\mathbf{v}\).
Solución
\[ \begin{align*} \mathbf{u}\times \mathbf{v} &= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix}=\begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ -2&1&1\\ 3&-1&1\\ \end{vmatrix} \\[4pt] &=\hat{\mathbf{i}}(1+1)-\hat{\mathbf{j}}(-2-3)+\hat{\mathbf{k}}(2-3) \\[4pt] &=\displaystyle{\color{Maroon}2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}-\hat{\mathbf{k}}} \end{align*} \nonumber\]
Para verificar que dos vectores son perpendiculares realizamos el producto punto:
\[\mathbf{u} \cdot \mathbf{w}=(-2)(2)+(1)(5)+(1)(-1)=0 \nonumber\]
\[\mathbf{v} \cdot \mathbf{w}=(3)(2)+(-1)(5)+(1)(-1)=0 \nonumber\]
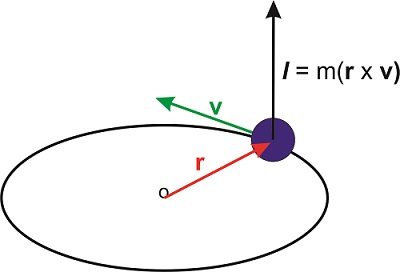
Una aplicación importante del producto cruzado implica la definición del momento angular. Si una partícula con masa\(m\) mueve una velocidad\(\mathbf{v}\) (un vector), su momento (lineal) es\(\mathbf{p}=m\mathbf{v}\). Dejar\(\mathbf{r}\) ser la posición de la partícula (otro vector), entonces el momento angular de la partícula se define como
\[\mathbf{l}=\mathbf{r}\times\mathbf{p} \nonumber\]
El momento angular es, por lo tanto, un vector perpendicular a ambos\(\mathbf{r}\) y\(\mathbf{p}\). Debido a que la posición de la partícula necesita definirse con respecto a un origen particular, este origen debe especificarse al definir el momento angular.
Normalización vectorial
Un vector de cualquier longitud dada se puede dividir por su módulo para crear un vector unitario (es decir, un vector de longitud unitaria). Veremos aplicaciones de vectores unitarios (o normalizados) en el siguiente capítulo.
Por ejemplo, el vector
\[\mathbf{u}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+i\hat{\mathbf{k}} \nonumber\]
tiene una magnitud:
\[|\mathbf{u}|^2=1^2+1^2+(-i)(i)=3\rightarrow |\mathbf{u}|=\sqrt{3} \nonumber\]
Por lo tanto, para normalizar este vector dividimos todos los componentes por su longitud:
\[\hat{\mathbf{u}}=\frac{1}{\sqrt{3}}\hat{\mathbf{i}}+\frac{1}{\sqrt{3}}\hat{\mathbf{j}}+\frac{i}{\sqrt{3}}\hat{\mathbf{k}} \nonumber\]
Observe que usamos el “sombrero” para indicar que el vector tiene longitud unitaria.
¿Necesitas ayuda? Los enlaces a continuación contienen ejemplos resueltos.
Operaciones con vectores: http://tinyurl.com/mw4qmz8
Enlaces externos:
- El producto punto: http://patrickjmt.com/vectors-the-dot-product/
- El producto cruzado: http://patrickjmt.com/the-cross-product/
- El producto de punto y cruz: http://www.youtube.com/watch?v=enr7JqvehJs

