1.1: Por qué es necesaria la mecánica cuántica

El campo de la química teórica se ocupa de las estructuras, enlaces, reactividad y propiedades físicas de átomos, moléculas, radicales e iones, todos cuyos tamaños van desde aproximadamente 1 Å para átomos y moléculas pequeñas hasta unos pocos cientos Å para polímeros y moléculas biológicas como ADN y proteínas. A veces, estos bloques de construcción se combinan para formar materiales nanoscópicos (por ejemplo, puntos cuánticos, láminas de grafeno) cuyas dimensiones abarcan hasta miles de Å, haciéndolos susceptibles de detección utilizando herramientas microscópicas especializadas. Sin embargo, se ha encontrado que la descripción de los movimientos y propiedades de las partículas que comprenden sistemas tan pequeños no es susceptible de tratamiento mediante mecánica clásica. Sus estructuras, energías y otras propiedades solo han sido descritas con éxito en el marco de la mecánica cuántica. Es por ello que la mecánica cuántica tiene que ser dominada como parte del aprendizaje de la química teórica.

Sabemos que todas las moléculas están hechas de átomos que, a su vez, contienen núcleos y electrones. Como discuto en este Capítulo, las ecuaciones que gobiernan los movimientos de electrones y de núcleos no son las ecuaciones familiares de Newton

\[\textbf{F} = m \textbf{a} \tag{1.1}\]

sino un nuevo conjunto de ecuaciones llamadas ecuaciones de Schrödinger. Cuando los científicos estudiaron por primera vez el comportamiento de los electrones y núcleos, intentaron interpretar sus hallazgos experimentales en términos de movimientos newtonianos clásicos, pero tales intentos finalmente fracasaron. Encontraron que esas pequeñas partículas de luz se comportaban de una manera que simplemente no es consistente con las ecuaciones de Newton. Permítanme ahora ilustrar algunos de los datos experimentales que dieron origen a estas paradojas y mostrarles cómo los científicos de aquellos primeros tiempos utilizaron entonces estos datos para sugerir nuevas ecuaciones que estas partículas podrían obedecer. Quiero recalcar que la ecuación de Schrödinger no fue derivada sino postulada por estos científicos. De hecho, hasta la fecha, a mi entender, nadie ha podido derivar la ecuación de Schrödinger.

A partir del trabajo pionero de Bragg sobre difracción de rayos X a partir de planos de átomos o iones en cristales, se supo que los picos en la intensidad de los rayos X difractados que tienen longitud de onda l se producirían en ángulos de dispersión q determinados por la famosa ecuación de Bragg:

\[n \lambda = 2 d \sin{\theta} \tag{1.2}\]

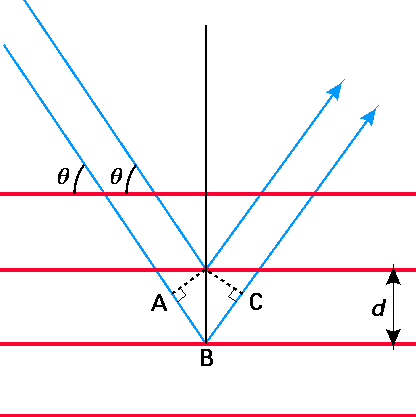
donde d es el espaciamiento entre planos vecinos de átomos o iones. Estas cantidades se ilustran en la Figura 1.1 que se muestra a continuación. Pueden existir tales picos de difracción, cada uno marcado por un valor diferente del entero\(n\) (\(n = 1, 2, 3, \cdots\)). La fórmula de Bragg se puede derivar considerando cuándo dos fotones, uno disperso desde el segundo plano en la figura y el segundo desde el tercer plano, sufrirán interferencia constructiva. Esta condición se cumple cuando la longitud de trayectoria adicional cubierta por el segundo fotón (es decir, la longitud de puntos\(A\)\(B\) a\(C\)) es un múltiplo entero de la longitud de onda de los fotones.

Figura 1.1. Dispersión de dos haces en ángulo\(\theta\) desde dos planos en un cristal espaciado por d.

La importancia de estos experimentos de dispersión de rayos X para electrones y núcleos aparece en los experimentos de Davisson y Germer en 1927 quienes dispersaron electrones de (razonablemente) energía cinética fija\(E\) de cristales metálicos. Estos trabajadores encontraron que las gráficas del número de electrones dispersos en función del ángulo de dispersión\(\theta\) mostraban picos en ángulos\(\theta\) que obedecían una ecuación similar a Bragg. Lo sorprendente de esta observación es que los electrones son partículas, sin embargo, la ecuación de Bragg se basa en las propiedades de las ondas. Una observación importante derivada de los experimentos de Davisson-Germer fue que los ángulos de dispersión\(\theta\) observados para electrones de energía cinética\(E\) podrían ajustarse a la ecuación de Bragg si se atribuyera a estos electrones una longitud de onda definida por

\[\lambda = \dfrac{h}{\sqrt{2m_e E}} \tag{1.3}\]

donde\(m_e\) está la masa del electrón y h es la constante introducida por Max Planck y Albert Einstein a principios del siglo XX para relacionar la energía\(E\) de un fotón con su frecuencia\(\nu\) vía\(E = h\nu\)). Estos sorprendentes hallazgos fueron algunos de los primeros en sugerir que los electrones, que siempre habían sido vistos como partículas, podrían tener algunas propiedades generalmente atribuidas a las ondas. Es decir, como ha sugerido de Broglie en 1925, un electrón parece tener una longitud de onda inversamente relacionada con su momento, y mostrar difracción de tipo onda. Debo mencionar que también se observó difracción análoga cuando otras partículas pequeñas de luz (por ejemplo, protones, neutrones, núcleos e iones atómicos pequeños) se dispersaron de planos cristalinos. En todos estos casos, se observa difracción similar a Bragg y se encuentra que la ecuación de Bragg gobierna los ángulos de dispersión si se asigna una longitud de onda a la partícula de dispersión de acuerdo con

\[\lambda = \dfrac{h}{\sqrt{2m E}} \tag{1.4}\]

donde

• \(m\)es la masa de la partícula dispersa y
• \(h\)es la constante de Planck (6.62 x10 ^-27 erg seg).

La observación de que los electrones y otras pequeñas partículas de luz muestran un comportamiento de onda fue importante porque estas partículas son de lo que están hechos todos los átomos y moléculas. Entonces, si queremos comprender completamente los movimientos y el comportamiento de las moléculas, debemos estar seguros de que podemos describir adecuadamente tales propiedades para sus constituyentes. Debido a que las ecuaciones newtonianas clásicas no contienen factores que sugieran propiedades de onda para electrones o núcleos que se mueven libremente en el espacio, los comportamientos anteriores presentaron desafíos significativos.

Otro problema que surgió en los primeros estudios de átomos y moléculas resultó del estudio de los fotones emitidos por átomos e iones que habían sido calentados o excitados de otra manera (por ejemplo, por descarga eléctrica). Se encontró que cada tipo de átomo (es decir, H o C u O) emitía fotones cuyas frecuencias\(\nu\) eran de valores muy característicos. Un ejemplo de tales espectros de emisión se muestra en la Figura 1.2 para átomos de hidrógeno.

Figura 1.2. Espectro de emisión de hidrógeno atómico con algunas líneas repetidas a continuación para ilustrar las series a las que pertenecen.

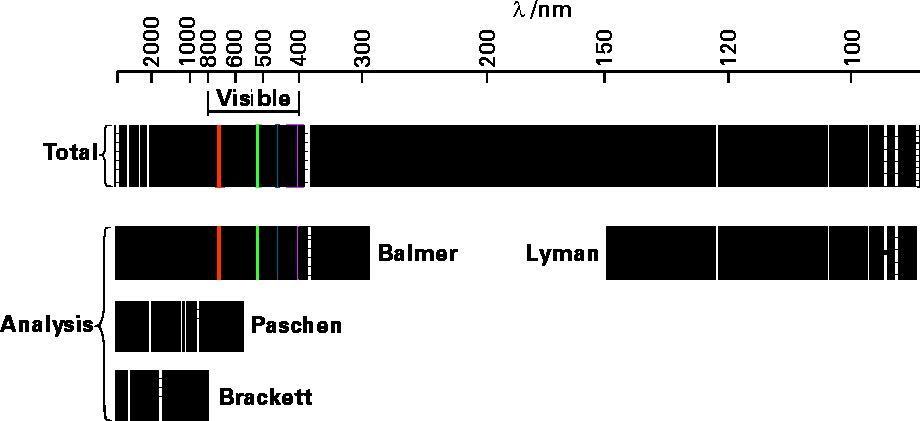
En el panel superior, vemos todas las líneas emitidas con sus longitudes de onda indicadas en nanómetros. Los otros paneles muestran cómo estas líneas han sido analizadas (por científicos cuyos nombres están asociados) en patrones que se relacionan con los niveles de energía específicos entre los cuales se producen transiciones para emitir los fotones correspondientes.

En los primeros intentos de racionalizar tales espectros en términos de movimientos electrónicos, se describió un electrón como moviéndose alrededor de los núcleos atómicos en órbitas circulares como se muestra en la Figura 1. 3.

Figura 1.3: Caracterización de órbitas estables pequeñas y grandes para un electrón que se mueve alrededor de un núcleo.

Se pensó que una órbita circular era estable cuando la fuerza centrífuga externa caracterizada por el radio\(r\) y la velocidad\(v\) (\(m_e v^2/r\)) sobre el electrón contrarrestaba perfectamente la fuerza Coulomb atractiva hacia adentro (\(Ze^2/r^2\)) ejercida por el núcleo de carga\(Z\):

\[m_e \dfrac{v^2}{r} = \dfrac{Ze^2}{r^2} \tag{1.5}\]

Esta ecuación, a su vez, permite relacionar la energía\(\dfrac{1}{2} m_e v^2\) cinética con la energía coulómbica\(Ze^2/r\), y así expresar la energía total\(E\) de una órbita en términos del radio de la órbita:

\[E = \dfrac{1}{2} m_e v^2 – \dfrac{Ze^2}{r^2} = -\dfrac{1}{2} \dfrac{Ze^2}{r^2} \tag{1.6}\]

La energía que caracteriza una órbita o radio\(r\), en relación con la\(E = 0\) referencia de energía en\(r \rightarrow \infty\), se vuelve cada vez más negativa (es decir, cada vez más baja) a medida que\(r\) se vuelve más pequeña. Esta relación entre las fuerzas externas e internas permite concluir que el electrón debe moverse más rápido a medida que se acerca al núcleo desde entonces\(v^2 = Ze^2/(r m_e)\). Sin embargo, en ninguna parte de este modelo hay un concepto que se relacione con el hecho experimental de que cada átomo emite sólo ciertos tipos de fotones. Se creía que la emisión de fotones se producía cuando un electrón que se movía en una órbita circular más grande perdió energía y se trasladó a una órbita circular más pequeña. Sin embargo, la dinámica newtoniana que produjo la ecuación anterior permitiría seguir órbitas de cualquier radio, y por lo tanto de cualquier energía. Así, parecería que el electrón debería poder emitir fotones de cualquier energía a medida que se desplazaba de órbita en órbita.

El avance que permitió a científicos como Niels Bohr aplicar el modelo de órbita circular a los datos espectrales observados implicó introducir primero la idea de que el electrón tiene una longitud de onda y que esta longitud de onda l está relacionada con su impulso por la ecuación de Broglie\(\lambda = h/p\). El paso clave en el modelo de Bohr fue especificar también que el radio de la órbita circular sea tal que la circunferencia del círculo\(2\pi r\) sea igual a un entero (\(n\)) múltiplo de la longitud de onda\(\lambda\). Solo de esta manera la onda del electrón experimentará interferencia constructiva a medida que el electrón orbita el núcleo. Así, la relación de Bohr que es análoga a la ecuación de Bragg que determina en qué ángulos puede ocurrir la interferencia constructiva es

\[2 \pi r = n \lambda. \tag{1.7}\]

Tanto esta ecuación como la ecuación análoga de Bragg son ilustraciones de lo que llamamos condiciones límite; son condiciones extra colocadas en la longitud de onda para producir algún carácter deseado en la onda resultante (en estos casos, interferencia constructiva). Por supuesto, queda la pregunta de por qué se deben imponer estas condiciones extras cuando la dinámica de Newton no las requiere. La resolución de esta paradoja es una de las cosas que hace la mecánica cuántica.

Volviendo al análisis anterior y utilizando\(\lambda = h/p = h/(m_e v)\)\(2\pi r = n\lambda\), así como la ecuación de fuerza-equilibrio\(m_e v^2/r = Ze^2/r^2\), uno puede entonces resolver para los radios que obedecen órbitas estables de Bohr:

\[r = \left(\dfrac{nh}{2\pi}\right)^2 \dfrac{1}{m_e Z e^2} \tag{1.8}\]

y, a su vez, para las velocidades de los electrones en estas órbitas

\[v = \dfrac{Z e^2}{nh/2\pi}. \tag{1.9}\]

Estos dos resultados permiten entonces expresar la suma de las energías cinética (\(\dfrac{1}{2} m_e v^2\)) y potencial de Coulomb (\(-Ze^2/r\)) como

\[E = -\dfrac{1}{2} m_e Z^2 \dfrac{e^4}{(nh/2\pi)^2}. \tag{1.10}\]

Así como en el resultado de la difracción de Bragg, que especificaba en qué ángulos se produjeron altas intensidades especiales en la dispersión, hay muchas órbitas estables de Bohr, cada una etiquetada por un valor del entero\(n\). Aquellos con pequeños radios\(n\) tienen radios pequeños (escalado as\(n^2\)), altas velocidades (escalado como 1/n) y energías totales más negativas (n.b., el cero de referencia de energía corresponde al electrón at\(r = \infty\), y con\(v = 0\)). Entonces, es el resultado de que solo se permiten ciertas órbitas lo que hace que solo se produzcan ciertas energías y así solo se observen ciertas energías en los fotones emitidos.

Resultó que la fórmula de Bohr para los niveles de energía (etiquetados por\(n\)) de un electrón que se mueve alrededor de un núcleo podría usarse para explicar los espectros de emisión de líneas discretas de todos los átomos e iones de un electrón (es decir\(H\)\(He^+\),,\(Li^{+2}\),, etc., a veces llamados especies hidrogénicas) a muy alta precisión. En tal interpretación de los datos experimentales, se afirma que un fotón de energía

\[h\nu = R \left(\dfrac{1}{n_i^2} – \dfrac{1}{n_f^2}\right) \tag{1.11}\]

se emite cuando el átomo o ion experimenta una transición de una órbita que tiene número cuántico\(n_i\) a una órbita de menor energía que tiene\(n_f\). Aquí el símbolo\(R\) se utiliza para denotar la siguiente colección de factores:

\[R = \dfrac{1}{2} m_e Z^2 \dfrac{e^4}{\Big(\dfrac{h}{2\pi}\Big)^2} \tag{1.12}\]

y se llama la unidad de energía Rydberg y es igual a 13.6 eV.

La fórmula de Bohr para los niveles de energía no coincidió también con el patrón observado de espectros de emisión para especies que contenían más de un solo electrón. Sin embargo, da un ajuste razonable, por ejemplo, a los espectros de átomos de Na si se examinan solo las transiciones que involucran solo el electrón de valencia 3s único. Además, se puede mejorar mucho si se introduce una modificación diseñada para tratar la penetración de los orbitales 3s y superiores del átomo de Na dentro de las regiones del espacio ocupadas por los orbitales 1s, 2s y 2p. Tal modificación al modelo de Bohr se logra introduciendo la idea de un llamado defecto cuántico d en el número cuántico principal para\(n\) que la expresión\(n\) de la dependencia de los orbitales cambie a

\[E = \dfrac{-R}{(n-\delta)^2} \tag{1.13}\]

Ejemplo 1.1

Por ejemplo, eligiendo\(\delta\) igual a 0.41, 1.37, 2.23, 3.19 o 4.13 para Li, Na, K, Rb y Cs, respectivamente, en esta llamada fórmula de Rydberg, se encuentra un acuerdo decente entre la\(n\) -dependencia de los espaciamientos energéticos de los estados de valencia excitados por separado de estos átomos. El hecho de que\(\delta\) sea más grande para Na que para Li y mayor para Cs refleja el hecho de que el orbital 3s de Na penetra en los proyectiles 1s, 2s y 2p mientras que el orbital 2s de Li penetra solo en el caparazón 1s y el orbital 6s de Cs penetra\(n = \) 1, 2, 3, 4 y 5 proyectiles.

Resulta que esta fórmula de Rydberg también se puede aplicar a ciertos estados electrónicos de moléculas. En particular, para cationes de cubierta cerrada tales como\(NH_4^+\)\(H_3O^+\), alcoholes protonados y aminas protonadas (incluso en cadenas laterales de aminoácidos), se puede unir un electrón en un denominado orbital de Rydberg para formar radicales neutros correspondientes tales como\(NH_4\),\(H_3O\),\(R-NH_3\), o \(R-OH_2\). Por ejemplo, en\(NH_4\), el electrón unido a un núcleo\(NH_4^+\) catiónico subyacente. El estado de menor energía de esta especie de Rydberg a menudo se etiqueta 3s porque\(NH_4^+\) es isoelectrónico con el catión Na+ que une un electrón en su orbital 3s en su estado fundamental. Al igual que en el caso de los átomos alcalinos, estas moléculas de Rydberg también poseen estados electrónicos excitados. Por ejemplo, el radical NH4 tiene estados etiquetados como 3p, 3d, 4s, 4p, 4d, 4f, etc. Al hacer una elección apropiada del parámetro de defecto cuántico d, los espaciamientos de energía entre estos estados pueden ajustarse razonablemente bien a la fórmula de Rydberg (Ecuación 1.13). En la Figura 1.3.a se muestran varios orbitales de\(NH_4\) Rydberg de

Figura 1.3. a. Los orbitales\(n = 3\)\(4\),, y\(5\) Rydberg de\(NH_4\) con sus contornos más externos que contienen 60% de su densidad electrónica. Se supone que los orbitales más pequeños representan orbitales C-C, C-N o C-O para dar una perspectiva del tamaño de los\(\sigma^*\) orbitales de Rydberg.

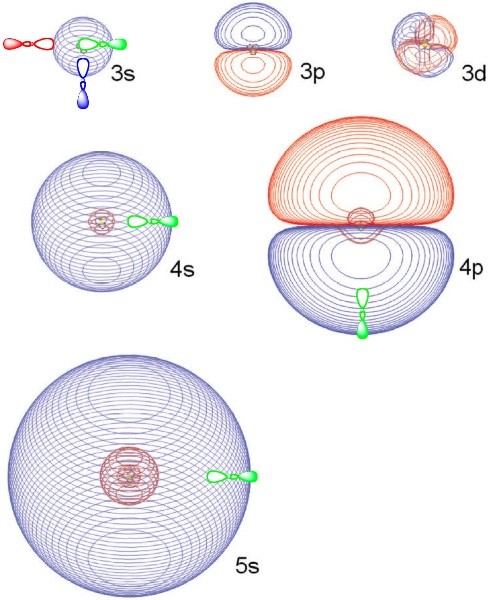
Estos orbitales de Rydberg pueden ser bastante grandes (sus tamaños se escalan ya que\(n^2\), claramente tienen las formas angulares s, p o d, y poseen el número esperado de nodos radiales. Sin embargo, para orbitales moleculares de Rydberg, y a diferencia de los orbitales atómicos de Rydberg\(p\), los orbitales tres\(d\)\(f\), cinco, siete, etc. no son degenerados, sino que se dividen en energía de una manera que refleja la simetría de la simetría del catión subyacente. Por ejemplo, for\(NH_4\), los tres\(3p\) orbitales son degenerados y pertenecen a la\(t_2\) simetría en el grupo de\(T_d\) puntos; los cinco\(3d\) orbitales se dividen en tres orbitales e degenerados\(t_2\) y dos degenerados.

Entonces, el modelo de Bohr funciona bien para átomos o iones de un electrón y la ecuación de Bohr modificada por defecto cuántico describe razonablemente bien algunos estados de átomos alcalinos y de moléculas de Rydberg. La razón principal de la descomposición de la fórmula de Bohr es el descuido de las repulsiones de Coulomb electrón-electrón en su derivación, las cuales se corrigen cualitativamente mediante el uso del parámetro de defecto cuántico para átomos y moléculas de Rydberg. Sin embargo, el éxito del modelo de Bohr dejó claro que los espectros de emisión discretos solo podían explicarse introduciendo el concepto de que no todas las órbitas estaban permitidas. Solo las órbitas especiales que obedecían una condición de interferencia constructiva eran realmente accesibles a los movimientos del electrón. Esta idea de que no todas las energías estaban permitidas, sino que solo podían ocurrir ciertas energías cuantificadas fue esencial para lograr incluso un sentido cualitativo de acuerdo con el hecho experimental de que los espectros de emisión eran discretos.

En resumen, dos observaciones experimentales sobre el comportamiento de los electrones que fueron cruciales para el abandono de la dinámica newtoniana fueron las observaciones de difracción de electrones y de espectros de emisión discretos. Ambos hallazgos parecen sugerir que los electrones tienen algunas características de onda y que estas ondas solo tienen ciertas longitudes de onda permitidas (es decir, cuantificadas).

Entonces, ahora tenemos alguna idea de por qué las ecuaciones de Newton no dan cuenta de los movimientos dinámicos de la luz y las partículas pequeñas como los electrones y los núcleos. Vemos que podrían imponerse condiciones adicionales (por ejemplo, la condición de Bragg o restricciones en la longitud de onda de Broglie) para lograr cierto grado de concordancia con la observación experimental. Sin embargo, todavía nos quedamos preguntándonos qué ecuaciones se pueden aplicar para describir adecuadamente tales movimientos y por qué se necesitan las condiciones adicionales. Resulta que era necesario desarrollar un nuevo tipo de ecuación basada en combinar las propiedades de onda y partícula para abordar tales cuestiones. Estas son las llamadas ecuaciones de Schrödinger a las que ahora dirigimos nuestra atención.

Como dije antes, nadie ha demostrado todavía que la ecuación de Schrödinger siga deductivamente de alguna teoría más fundamental. Es decir, los científicos no derivaron esta ecuación; la postularon. Se puede tener alguna idea de cómo los científicos de esa época soñaron la ecuación de Schrödinger examinando la dependencia temporal y espacial que caracteriza a las llamadas olas viajeras. Cabe señalar que las personas que trabajaban en estos problemas sabían mucho sobre las olas (por ejemplo, las ondas sonoras y las ondas de agua) y las ecuaciones que obedecían. Además, sabían que las ondas a veces podían mostrar la característica de longitudes de onda o frecuencias cuantificadas (por ejemplo, fundamentos y armónicos en ondas sonoras). Sabían, por ejemplo, que las ondas en una dimensión que están restringidas en dos puntos (por ejemplo, una cuerda de violín sujeta fija en dos extremos) experimentan un movimiento oscilatorio en el espacio y el tiempo con frecuencias y longitudes de onda características. Por ejemplo, el movimiento de la cuerda de violín que se acaba de mencionar puede describirse como que tiene una amplitud\(A(x,t)\) en una posición a\(x\) lo largo de su longitud en el tiempo\(t\) dada por

\[A(x,t) = A(x,o) \cos(2\pi \nu t), \tag{1.14}\]

donde\(nu\) esta su frecuencia de oscilacion. La dependencia espacial de la amplitud también tiene una dependencia sinusoidal dada por

\[A(x,0) = A \sin (\dfrac{2\pi x}{\lambda}) \tag{1.15}\]

donde\(\lambda\) es la longitud de cresta a cresta de la ola. Dos ejemplos de tales ondas en una dimensión se muestran en la Figura 1. 4.

Figura 1.4. Notas fundamentales y primeras armónicas de una cuerda de violín de longitud\(L\).

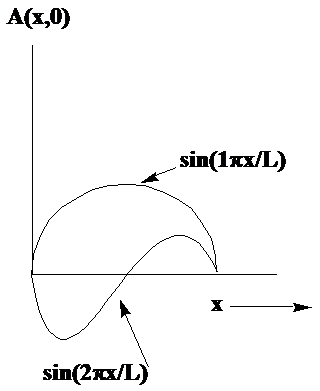
En estos casos, la cuerda se fija en\(x = 0\) y en\(x = L\), por lo que las longitudes de onda que pertenecen a las dos ondas mostradas son\(\lambda = 2L\) y\(\lambda = L\). Si la cuerda del violín no estuviera sujetada\(x = L\), las olas podrían tener algún valor de\(\lambda\). Sin embargo, debido a que la cadena está unida a\(x = L\), las longitudes de onda permitidas se cuantifican para obedecer

\[\lambda = \dfrac{2L}{n}, \tag{1.16}\]

donde\(n = 1, 2, 3, 4, \cdots\). La ecuación que obedecen tales ondas, llamada ecuación de onda, dice:

\[\dfrac{d^2A(x,t)}{dt^2} = c^2 \dfrac{d^2A}{dx^2} \tag{1.17}\]

donde\(c\) esta la velocidad a la que viaja la ola. Esta velocidad depende de la composición del material del que está hecha la cuerda de violín; el material rígido de la cuerda produce ondas con velocidades más altas que para el material más blando. Usando las expresiones anteriores para las\(t\) dependencias\(x-\) y de la onda\(A(x,t)\), encontramos que la frecuencia y longitud de onda de la onda están relacionadas por la llamada ecuación de dispersión:

\[\nu^2 = \left(\dfrac{c}{\lambda}\right)^2, \tag{1.18}\]

o

\[c = \lambda \nu. \tag{1.19}\]

Esta relación implica, por ejemplo, que una cuerda de instrumento hecha de un material muy rígido (grande\(c\)) producirá un tono de frecuencia más alto para una longitud de onda dada (es decir, un valor dado de\(n\)) que una cuerda hecha de un material más suave (más pequeño\(c\)).

Para las olas que se mueven sobre la superficie de, por ejemplo, una superficie rectangular bidimensional de longitudes\(L_x\) y\(L_y\), se encuentra

\[A(x,y,t) = \sin \left(n_x \dfrac{p_x}{L_x}\right) \sin\left(n_y \dfrac{p_y}{L_y}\right) \cos\left(2\pi \nu t\right). \tag{1.20}\]

Por lo tanto, las ondas se cuantifican en dos dimensiones porque sus longitudes de onda deben estar restringidas\(A(x,y,t)\) para hacer que desaparezcan en\(x = 0\) y así\(x = L_x\) como en\(y = 0\) y\(y = L_y\) para todo momento\(t\).

Es importante señalar, al cerrar esta discusión de ondas en cuerdas y superficies, que no está siendo una solución a la ecuación de Schrödinger lo que da como resultado la cuantificación de las longitudes de onda. En cambio, es la condición de que la onda desaparezca en los límites la que genera la cuantificación. Verás esta tendencia una y otra vez a lo largo de este texto; cuando una función de onda está sujeta a restricciones específicas en su límite interno o externo (o ambos), resultará la cuantificación; si estas condiciones límite no están presentes, la cuantificación no ocurrirá. Volvamos ahora al tema de las ondas que describen los electrones en movimiento.

Los pioneros de la mecánica cuántica examinaron formas funcionales similares a las mostradas anteriormente. Por ejemplo, formas como\(A = \exp[\pm 2\pi(\nu t – x/\lambda)]\) fueron consideradas porque corresponden a ondas periódicas que evolucionan en\(x\) y\(t\) bajo ninguna fuerza externa\(x\) o\(t\) dependiente. Al darse cuenta de que

\[\dfrac{d^2A}{dx^2} = - \left(\dfrac{2\pi}{\lambda} \right)^2 A \tag{1.21}\]

y usando la hipótesis de Broglie\(\lambda = h/p\) en la ecuación anterior, se encuentra

\[\dfrac{d^2A}{dx^2} = - p^2 \Big(\dfrac{2\pi}{h}\Big)^2 A. \tag{1.22}\]

Si\(A\) se supone que se relaciona con el movimiento de una partícula de impulso p bajo ninguna fuerza externa (ya que la forma de onda corresponde a este caso), se\(p^2\) puede relacionar con la energía\(E\) de la partícula por\(E = p^2/2m\). Entonces, la ecuación para se\(A\) puede reescribir como:

\[\dfrac{d^2A}{dx^2} = - 2m E \Big(\dfrac{2\pi}{h}\Big)^2 A, \tag{1.23}\]

o, alternativamente,

\[- \Big(\dfrac{h}{2\pi}\Big)^2 (\dfrac{1}{2}m) \dfrac{d^2A}{dx^2} = E A. \tag{1.23}\]

Volviendo a la dependencia del tiempo\(A(x,t)\) y el uso\(\nu = E/h\), también se puede demostrar que

\[i \Big(\dfrac{h}{2\pi}\Big) \dfrac{dA}{dt} = E A, \tag{1.24}\]

lo que, utilizando el primer resultado, sugiere que

\[i \Big(\dfrac{h}{2\pi}\Big) \dfrac{dA}{dt} = - \Big(\dfrac{h}{2\pi}\Big)^2 (\dfrac{1}{2}m) \dfrac{d^2A}{dx^2}. \tag{1.25}\]

Esta es una forma primitiva de la ecuación de Schrödinger que abordaremos con mucho más detalle a continuación. Brevemente, lo que es importante tener en cuenta que el uso de las conexiones de Broglie y Planck/Einstein (\(\lambda = h/p\)y\(E = h\nu\)), ambas que involucran la constante h, produce sugestivas conexiones entre

\[i \Big(\dfrac{h}{2\pi}\Big) \dfrac{d}{dt} \text{ and } E \tag{1.26}\]

y entre

\[p^2 \text {and } – \Big(\dfrac{h}{2\pi}\Big)^2 \dfrac{d^2}{dx^2} \tag{1.27}\]

o, alternativamente, entre

\[p \text{ and } – i \Big(\dfrac{h}{2\pi}\Big) \dfrac{d}{dx}.\tag{1.28}\]

Estas conexiones entre las propiedades físicas (energía\(E\) e impulso\(p\)) y los operadores diferenciales son algunas de las características inusuales de la mecánica cuántica.

La discusión anterior sobre las ondas y longitudes de onda cuantificadas, así como las observaciones sobre la ecuación de onda y los operadores diferenciales no pretenden proporcionar o incluso sugerir una derivación de la ecuación de Schrödinger. Nuevamente los científicos que inventaron la mecánica cuántica no derivaron sus ecuaciones de trabajo. En cambio, las ecuaciones y reglas de la mecánica cuántica han sido postuladas y diseñadas para ser consistentes con las observaciones de laboratorio. Mis alumnos a menudo encuentran esto desconcertante porque esperan y buscan una base fundamental subyacente a partir de la cual las leyes básicas de la mecánica cuántica siguen lógicamente. Trato de recordarles que no es así como funciona la teoría. En cambio, uno usa la observación experimental para postular una regla o ecuación o teoría, y luego se prueba la teoría haciendo predicciones que pueden ser probadas por experimentos adicionales. Si la teoría falla, debe ser refinada, y este proceso continúa hasta que se tiene una teoría cada vez mejor. En este sentido, la mecánica cuántica, con todas sus inusuales construcciones y reglas matemáticas, debe ser vista como derivada de la imaginación de científicos que intentaron inventar una teoría que fuera consistente con datos experimentales y que pudiera usarse para predecir cosas que luego podrían ser probadas en el laboratorio . Hasta el momento, esta teoría ha demostrado ser confiable, pero, por supuesto, siempre estamos buscando una teoría nueva y mejorada que describa cómo se mueven las pequeñas partículas de luz.

Si te ayuda a aceptar más la teoría cuántica, debo señalar que la descripción cuántica de las partículas se reduce a la descripción clásica de Newton bajo ciertas circunstancias. En particular, cuando se tratan partículas pesadas (por ejemplo, masas macroscópicas e incluso átomos más pesados), a menudo es posible usar la dinámica de Newton. Pronto, discutiremos con más detalle cómo coinciden a veces la dinámica cuántica y la clásica (en cuyo caso uno es libre de usar la dinámica Newton más simple). Entonces, pasemos ahora a ver esta extraña ecuación de Schrödinger de la que llevamos tanto tiempo divagando.

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

• Integrated by Tomoyuki Hayashi (UC Davis)