1.4: Movimientos de Partículas Libres en Más Dimensiones
- Page ID
- 70967
El número de dimensiones depende del número de partículas y del número de dimensiones espaciales (y otras) necesarias para caracterizar la posición y el movimiento de cada partícula. El número de dimensiones también afecta el número de números cuánticos que pueden usarse para etiquetar estados propios del Hamiltoniano.
Ecuación de Schrödinger
Considere un electrón de masa m y carga\(e\) moviéndose sobre una superficie bidimensional que define el\(x,y\) plano (por ejemplo, tal vez un electrón está restringido a la superficie de un sólido por un potencial que lo une fuertemente a una región estrecha en la\(z\) dirección -pero le permite vagar libremente sobre un área rectangular en el\(x,y\) plano), y asumir que el electrón experimenta un potencial constante y no variable en el tiempo\(V_0\) en todos los puntos de este plano. Por ejemplo, si\(V_0\) es negativo, podría reflejar la energía de unión del electrón en relación con su energía en vacío.
La ecuación pertinente de Schrödinger independiente del tiempo es:
\[- \dfrac{\hbar^2}{2m} \left(\dfrac{\partial^2}{\partial x^2} +\dfrac{\partial^2}{\partial y^2}\right)\psi(x,y) +V_0 \psi(x,y) = E\psi(x,y).\]
La tarea en cuestión es resolver la ecuación de valor propio anterior para determinar los estados de energía permitidos para este electrón. Debido a que no hay términos en esta ecuación que acoplen el movimiento en las\(y\) direcciones\(x\) y (por ejemplo, no hay términos de la forma\(x^ay^b\)\(x\dfrac{\partial}{\partial y}\) o o\(\psi\dfrac{\partial}{\partial x}\)), la separación de variables se puede utilizar para escribir\(y\) como un producto\(\psi(x,y)=A(x)B(y)\). La sustitución de esta forma en la ecuación de Schrödinger, seguida de reunir todos los términos\(x\) dependientes y todos los términos dependientes de y, da;
\[- \dfrac{\hbar^2}{2m} \frac{1}{A}\frac{\partial^2 A}{\partial x^2} - \dfrac{\hbar^2}{2m} \frac{1}{B}\frac{\partial^2 B}{\partial y^2} = E-V_0.\]
Dado que el primer término no contiene\(y\) -dependencia y el segundo no contiene\(x\) -dependencia, y debido a que el lado derecho de la ecuación es independiente de ambos\(x\) y\(y\), ambos términos de la izquierda deben ser realmente constantes (estas dos constantes se denotan\(E_x\) y\(E_y\), respectivamente, dándose cuenta de que tienen unidades de energía). Esta observación permite escribir dos ecuaciones de Schrödinger separadas:
\[- \dfrac{\hbar^2}{2m} \frac{1}{A}\frac{\partial^2 A}{\partial x^2} = E_x\]
y
\[- \dfrac{\hbar^2}{2m} \frac{1}{B}\frac{\partial^2 B}{\partial y^2} = E_y.\]
La energía total\(E\) puede entonces expresarse en términos de estas energías separadas\(E_x\) y\(E_y\) de\(E_x + E_y = E-V_0\). Las soluciones a las ecuaciones\(x-\) y\(y-\) Schrödinger se ven fácilmente como:
\[A(x) = \exp\left(ix\sqrt{\frac{2mE_x}{\hbar^2}}\right) \text{and} \exp\left(-ix\sqrt{\frac{2mE_x}{\hbar^2}}\right)\]
\[B(y) = \exp\left(iy\sqrt{\frac{2mE_y}{\hbar^2}}\right) \text{and} \exp\left(-iy\sqrt{\frac{2mE_y}{\hbar^2}}\right).\]
Se obtienen dos soluciones independientes para cada ecuación porque las ecuaciones de Schrödinger\(x-\) y el\(y-\) espacio son ambas ecuaciones diferenciales de segundo orden (es decir, una ecuación diferencial de segundo orden tiene dos soluciones independientes).
Condiciones de Límite
Las condiciones límite, no la ecuación de Schrödinger, determinan si los valores propios serán discretos o continuos
Si el electrón está completamente libre dentro del\(x,y\) plano, las energías\(E_x\) y\(E_y\) pueden asumir cualquier valor; esto significa que el experimentador puede inyectar el electrón en el\(x,y\) plano con cualquier energía total\(E\) y cualquier componente\(E_x\) y\(E_y\) a lo largo de los dos ejes siempre y cuando\(E_x + E_y = E\). En tal situación, se habla de las energías a lo largo de ambas coordenadas como que están en el continuo o no cuantificadas.
Por el contrario, si el electrón está obligado a permanecer dentro de un área fija en el\(x,y\) plano (por ejemplo, una región rectangular o circular), entonces la situación es cualitativamente diferente. La restricción del electrón a cualquier área especificada da lugar a condiciones de límite que imponen requisitos adicionales sobre lo anterior\(A\) y\(B\) funciones. Estas restricciones pueden surgir, por ejemplo, si el potencial\(V(x,y)\) se vuelve muy grande para\(x,y\) valores fuera de la región, en cuyo caso, la probabilidad de encontrar el electrón fuera de la región es muy pequeña. Tal caso podría representar, por ejemplo, una situación en la que la estructura molecular de la superficie sólida cambia fuera de la región encerrada de una manera que es altamente repulsiva para el electrón (por ejemplo, como en el caso de los corrales moleculares en superficies metálicas). Este caso podría entonces representar un modelo simple de los llamados corrales en los que la partícula está restringida a una región finita del espacio.
Por ejemplo, si el movimiento está restringido para que tenga lugar dentro de una región rectangular definida por\(0 \le x\le L_x\);\(0 \le y\le L_y\), entonces la propiedad de continuidad que todas las funciones de onda deben obedecer (debido\(A(x)\) a su interpretación como densidades de probabilidad, que deben ser continuas) hace que desaparezca en 0 y en \(L_x\). Es decir, porque\(A\) debe desaparecer para\(x < 0\) y debe desaparecer para\(x > L_x\), y porque\(A\) es continuo, debe desaparecer en\(x = 0\) y en\(x = L_x\). Asimismo,\(B(y)\) debe desaparecer a 0 y a las\(L_y\). Para implementar estas restricciones\(A(x)\), se deben combinar linealmente las dos soluciones anteriores\(\exp\left(ix\sqrt{\dfrac{2mE_x}{\hbar^2}}\right)\) y\(\exp\left(-ix\sqrt{\dfrac{2mE_x}{\hbar^2}}\right) \) lograr una función que se desvanezca en\(x=0\):
\[A(x) = \exp\left(ix\sqrt{\frac{2mE_x}{\hbar^2}}\right) - \exp\left(-ix\sqrt{\frac{2mE_x}{\hbar^2}}\right).\]
Se permite combinar linealmente soluciones de la ecuación de Schrödinger que tienen la misma energía (es decir, son degeneradas) porque las ecuaciones de Schrödinger son ecuaciones diferenciales lineales. Se debe aplicar un proceso análogo\(B(y)\) para lograr una función que se desvanece en\(y=0\):
\[B(y) = \exp\left(iy\sqrt{\frac{2mE_y}{\hbar^2}}\right) - \exp\left(-iy\sqrt{\frac{2mE_y}{\hbar^2}}\right).\]
Además requiriendo\(A(x)\) y\(B(y)\) desaparecer, respectivamente, en\(x=L_x\) y\(y=L_y\), respectivamente, da ecuaciones que solo pueden obedecerse si\(E_x\) y\(E_y\) asumen valores particulares:
\[ \exp\left( iL_x \sqrt{\frac{2mE_x}{\hbar^2}} \right)-\exp\left(-iL_x\sqrt{\frac{2mE_x}{\hbar^2}}\right)=0\text{, and}\]
\[ \exp \left( iL_y \sqrt{\frac{2mE_y}{\hbar^2}} \right) - \exp \left(-iL_y\sqrt{\frac{2mE_y}{\hbar^2}} \right) = 0.\]
Estas ecuaciones son equivalentes (es decir, usando\(\exp(ix) = \cos(x) + i \sin(x)\)) a
\[\sin\left(L_x\sqrt{\frac{2mE_x}{\hbar^2}}\right) = \sin\left(L_y\sqrt{\frac{2mE_y}{\hbar^2}}\right) = 0.\]
Sabiendo que se\(\sin(\theta)\) desvanece en\(q = n\pi\), para\(n=1,2,3,\cdots,\) (aunque la\(\sin(n\pi)\) función se desvanece para\(n=0\), esta función se desvanece para todos\(x\) o\(y\), y por lo tanto es inaceptable porque representa densidad de probabilidad cero en todos los puntos del espacio) se concluye que el energías\(E_x\) y solo\(E_y\) pueden asumir valores que obedecen:
\[L_x\sqrt{\frac{2mE_x}{\hbar^2}} =n_x\pi,\]
\[L_y\sqrt{\frac{2mE_y}{\hbar^2}} =n_y\pi\]
o
\[E_x = \frac{n_x^2\pi^2 \hbar^2}{2mL_x^2}\]
y
\[E_y = \frac{n_y^2\pi^2 \hbar^2}{2mL_y^2}, \text{ with } n_x \text{ and } n_y =1,2,3, \cdots\]
y
\[E = V_0 +E_x+ E_y.\]
Es importante destacar que es la imposición de condiciones límite, expresando el hecho de que el electrón está restringido espacialmente, lo que da lugar a energías cuantificadas. En ausencia de confinamiento espacial, o con confinamiento sólo en\(x = 0\) o\(L_x\) o sólo en\(y = 0\) o\(L_y\), las energías cuantificadas no se realizarían.
En este ejemplo, el confinamiento del electrón a un intervalo finito a lo largo de las\(y\) coordenadas\(x\) y produce energías que se cuantifican a lo largo de ambos ejes. Si el electrón estuviera confinado a lo largo de una coordenada (por ejemplo, entre\(0 \le x\le L_x\)) pero no a lo largo de la otra (\(B(y)\)es decir, está restringido a desaparecer solo en\(y=0\)\(y=L_y\) o en o en ningún punto), entonces la energía total\(E\) se encuentra en el continuo; su\(E_x\) componente se cuantifica pero \(E_y\)no lo es. Los análogos de tales casos surgen, por ejemplo, para una molécula triatómica que contiene un enlace fuerte y otro débil. Si el vínculo con la mayor energía de disociación se excita a un nivel que no es suficiente para romperlo pero que es superior a la energía de disociación del enlace más débil, se tiene una situación que resulta especialmente interesante. En este caso, uno tiene dos estados degenerados
- uno con el enlace fuerte que tiene alta energía interna y el enlace débil que tiene baja energía (\(\psi_1\)), y
- un segundo con el vínculo fuerte teniendo poca energía y el enlace débil teniendo energía más que suficiente para romperlo (\(\psi_2\)).
Aunque un experimento puede preparar la molécula en un estado que contiene solo el primer componente (es decir,\(\Psi(t=0)= C_1\psi_1 + C_2\psi_2\) con\(C_1 = 1\),\(C_2 = 0\)), el acoplamiento entre las dos funciones degeneradas (inducidas por términos en la H hamiltoniana que han sido ignorados en la definición\(\psi_1\) y\(\psi_2\)) puede causar la función de onda verdadera\(\Psi = \exp(-itH/\hbar) \Psi(t=0)\) para adquirir un componente de la segunda función a medida que evoluciona el tiempo. En tal caso, se habla de relajación interna de energía vibratoria (IVR) dando lugar a la descomposición unimolecular de la molécula.
Energías y funciones de onda para estados unidos
Para los niveles de energía discretos, las energías son funciones especificadas que dependen de números cuánticos, una por cada grado de libertad que se cuantifica
Volviendo a la situación en la que el movimiento está restringido a lo largo de ambos ejes, las energías totales resultantes y las funciones de onda (obtenidas insertando los niveles de energía cuántica en las expresiones para\(A(x)\) y\(B(y)\)) son las siguientes:
\[E_x = \frac{n_x^2\pi^2 \hbar^2}{2mL_x^2}\]
y
\[E_y = \frac{n_y^2\pi^2 \hbar^2}{2mL_y^2}\]
\[E = E_x + E_y +V_0\]
\[\psi(x,y) = \sqrt{\frac{1}{2L_x}}\sqrt{\frac{1}{2L_y}}\left[\exp\bigg(\frac{in_x\pi x}{L_x}\bigg) -\exp\bigg(-\frac{in_x\pi x}{L_x}\bigg)\right]\left[\exp\bigg(\frac{in_y\pi y}{L_y}\bigg) -\exp\bigg(-\frac{in_y\pi y}{L_y}\bigg)\right] \]
con\(n_x\) y\(n_y =1,2,3, \cdots\).
Se incluyen los dos\(\sqrt{\dfrac{1}{2L}}\) factores para garantizar que\(y\) se normaliza:
\[\int |\psi(x,y)|^2 dx,dy = 1.\]
La normalización\(|\psi(x,y)|^2\) permite identificarse adecuadamente como una densidad de probabilidad para encontrar el electrón en un punto\(x\),\(y\).
En la Figura 1. 13 se muestran gráficas de cuatro funciones de onda bidimensionales de este tipo para\(n_x\) y\(n_y\) valores de (1,1), (2,1), (1.2) y (2,2), respectivamente.
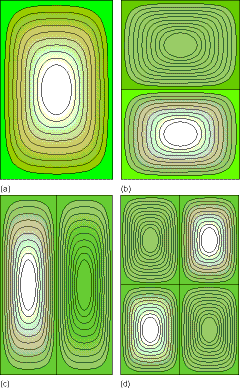
Tenga en cuenta que las funciones desaparecen en los límites de la caja, y observe cómo el número de nodos (es decir, ceros encontrados a medida que la función de onda oscila de positivo a negativo) se relaciona con los números\(n_x\) y\(n_y\) cuánticos y con la energía. Este patrón de más nodos que significan mayor energía es uno que nos encontramos una y otra vez en la mecánica cuántica y es algo que el estudiante debería poder usar para adivinar las energías relativas de las funciones de onda cuando sus tramas están a la mano. Por último, también debe notar que, como en el caso de la caja unidimensional, cualquier intento de interpretar clásicamente las probabilidades\(P(x,y)\) correspondientes a las funciones de onda cuántica anteriores dará como resultado un fallo. Como en el caso unidimensional, lo clásico\(P(x,y)\) sería constante a lo largo de rebanadas de fijas\(x\) y variables\(y\) o rebanadas de fijas\(y\) y variables\(x\) dentro de la caja porque la velocidad es constante allí. Sin embargo, las\(P(x,y)\) gráficas cuánticas, al menos para números cuánticos pequeños, no son constantes. Para los valores grandes\(P(x,y)\) y ny, las\(P(x,y)\) gráficas cuánticas volverán a acercarse, a través del principio de correspondencia cuántico-clásica, a la\(P(x,y)\) forma clásica (constante) excepto cerca de los puntos de inflexión clásicos (es decir, cerca de los bordes de la caja bidimensional).
Si, en lugar de estar confinado a un corral rectangular, el electrón se vio obligado a estar dentro de un círculo de radio R, la ecuación de Schrödinger se expresa más favorablemente en coordenadas polares\((r, \theta)\). Transformar las derivadas parciales que aparecen en la ecuación de Schrödinger
\[- \dfrac{\hbar^2}{2m} (\frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2})\psi(x,y) +V(x,y) \psi(x,y) = E\psi(x,y)\]
en coordenadas polares y darse cuenta de que el potencial depende de\(r\) pero no de\(\theta\) da
\[ - \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r}) +\frac{1}{r^2} \frac{\partial^2}{\partial \theta^2}) \psi(r, \theta) + V (r) \psi(r, \theta) = E\psi(r, \theta).\]
Nuevamente usando la separación de variables para sustituir
\[\psi(r, \theta) = A(r) B(\theta)\]
en la ecuación de Schrödinger y dividiendo por\(AB\), obtenemos
\[- \frac{1}{A} \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r})A(r)) +V_0 – \frac{1}{B} \dfrac{\hbar^2}{2m} (\frac{1}{r^2}\frac{\partial^2 B(\theta)}{\partial \theta^2}) = E\]
donde\(V_0\) es el valor del potencial dentro de la región circular. Los dos primeros términos a la izquierda y a la\(E\) derecha no contienen ninguna referencia a\(\theta\), por lo que la cantidad\(\dfrac{1}{B} \dfrac{\partial^2 B(\theta)}{\partial \theta^2}\) debe ser independiente de\(\theta\):
\[\frac{1}{B} \frac{\partial^2 B(\theta)}{\partial \theta^2} = c\]
Además, debido a que las coordenadas\((r, \theta)\) y\((r, \theta +2\pi)\) describen el mismo punto en el espacio,\(B(\theta)\) deben obedecer
\[B(\theta) = B(\theta +2 \pi).\]
Las soluciones a la ecuación diferencial anterior para\(B(\theta)\) sujeto a la condición de periodicidad son
\[B(\theta) = \frac{1}{\sqrt{2\pi}} \exp(± in \theta); n = 0, 1, 2, ….\]
Esto significa que la ecuación para la parte radial de la función de onda es
\[- \frac{1}{A} \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r})A(r)) +V_0 – \frac{1}{B}\dfrac{\hbar^2}{2m} (\frac{1}{r^2}n^2) = E\]
o
\[r^2 \frac{d^2A}{dr^2} + r \frac{dA}{dr} –n^2 A +\frac{2mr^2}{\hbar^2} (E-V_0)A = 0 .\]
Esta ecuación diferencial probablemente no te sea familiar, pero resulta que esta es la ecuación obedecida por las llamadas funciones de Bessel. Las funciones de Bessel etiquetadas\(J_n(ax)\) obedecen
\[x^2 \frac{d^2J}{dx^2} +x \frac{dJ}{dx} – n^2 J + a^2 x^2 J = 0\]
entonces, nuestra\(A\) función es
\[A(r) = J_n\left(\sqrt{\frac{2m(E-V_0)}{\hbar^2}}r\right).\]
Las funciones de onda completa son entonces
\[\psi(r, \theta) = A(r) B(\theta) = N J_n\left(\sqrt{\frac{2m(E-V_0)}{\hbar^2}}r\right) \frac{1}{\sqrt{2\pi}} \exp(± in \theta)\]
donde\(N\) es una constante de normalización. Los valores propios de energía\(E_{j,n}\) no pueden expresarse analíticamente como en el sistema de partículas en una caja (donde se utilizó el conocimiento de los ceros de la función de pecado para determinar\(E_n\)). Sin embargo, sabiendo que\(A(r)\) debe desaparecer en\(R = R\), podemos usar tablas (por ejemplo, ver Kreyszig, E. Advanced Engineering Mathematics, 8a ed.; John Wiley and Sons, Inc.: New York, 1999) que dan los valores de\(x\) a los que se\(J_n(x)\) desvanece para determinar el conjunto de valores propios asociados con cada valor del número cuántico de momento angular\(n\). En la tabla que se muestra a continuación, enumeramos los primeros cinco valores en los que\(J_0\)\(J_1\),, y\(J_2\) desaparecen.
Valores de\(x\) a los que se\(J_n(x)\) desvanecen para\(n = 0, 1\), y\(2\)
Si llamamos a los valores a los que se\(J_{n(x)}\) desvanece\(z_{n,j}\), entonces las energías se dan como
\[E_{n,j} = V_0 + \dfrac{(z_{n,j})^2 \hbar^2}{2mR^2}.\]
A partir del orden de los\(z_{n,j}\) valores mostrados en la tabla anterior, podemos ver que el orden de los niveles de energía será\(z_{0.1}\)\(z_{1,1}\),\( z_{1,2}\),\(z_{1,0}\),\(z_{1,1}\),\(z_{1,2}\),, y así sucesivamente, independientemente del tamaño del círculo\(R\) o de la masa de la partícula\(m\).
El estado con\(n = -1\) tiene la misma energía que con\(n = 1\); de igual manera,\(n = -2\) tiene la misma energía que\(n=2\). Entonces, todos menos los\(n = 0\) estados son doblemente degenerados; la única diferencia entre tales pares de estados es el sentido de los términos de momento angular\(\exp(\pm ni \theta)\). Estos niveles de energía dependen tanto del número cuántico de momento angular\(n\), como del número cuántico radial\(j\) y dependen de manera\(R\) muy similar a que las energías de partículas en una caja dependen de la longitud de la caja\(L\). En la Figura 1.13a se muestran gráficas de las densidades de probabilidad\(|\psi(r,\theta)|^2\) para\(n = 0, 1\), y para,\(2\) y para\(j = 1, 3\), y\(5\) para ilustrar cómo aumenta el número de nodos radiales a medida que\(j\) aumenta.

El carácter de\(|\psi(r,\theta)|^2\) también cambia con\(n\). Porque\(n = 0\), hay alta amplitud para que la partícula esté en el centro del círculo, pero para\(n > 0\), no hay amplitud en el centro. Esto es análogo a lo que se encuentra para los orbitales atómicos;\(s\) los orbitales tienen una amplitud distinta de cero en el núcleo, pero p, d, y los orbitales superiores no.
Examinemos algunos problemas más fáciles que pueden resolverse analíticamente hasta cierto punto. Esto ayudará a ilustrar cómo las condiciones de contorno generan la cuantificación y cómo el número de números cuánticos depende de la dimensionalidad del problema. Al considerar una partícula de masa\(m\) moviéndose en tres dimensiones pero restringida a permanecer dentro de una esfera de radio R, reemplazamos las tres coordenadas cartesianas\(x, y,\) y\(z\) por las coordenadas esféricas\(r\),\(\theta\), y\(\phi\). Al hacerlo, cambia los términos de energía cinética de la ecuación de Schrödinger en lo que mostramos a continuación
\[-\frac{\hbar^2}{2mr^2}\left(\frac{\partial}{\partial r}\left(r^2\frac{\partial\psi}{\partial r}\right)\right) -\frac{\hbar^2}{2m} \frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial\theta}\right) -\frac{\hbar^2}{2m}\frac{1}{r^2\sin\theta}\frac{\partial^2 \psi}{\partial\phi^2}+ V(r)\psi = E\psi.\]
Tomando el potencial de ser\(V_0\) (una constante) para\(0 \le r \le R\), e infinito para\(r > R\), podemos usar nuevamente la separación de variables para avanzar en la resolución de esta ecuación diferencial tridimensional. Nosotros sustituimos
\[\psi(r,\theta,\phi) = Y_{L,M} (\theta,\phi) F(r)\]
en la ecuación de Schrödinger y teniendo en cuenta que las llamadas funciones armónicas esféricas\(Y_{L,M} (\theta,\phi)\) obedecen a lo siguiente:
\[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial Y_{L,M}}{\partial\theta}\right)+ \frac{1}{\sin^2\theta}\frac{\partial^2 Y_{L,M}}{\partial\phi^2}= - L(L+1) Y_{L,M}.\]
Esto reduce la ecuación de Schrödinger a una ecuación para la función radial\(F(r)\):
\[-\frac{\hbar^2}{2mr^2}\left(\frac{\partial}{\partial r}\left(r^2\frac{\partial F}{\partial r}\right)\right) + \frac{\hbar^2}{2mr^2}L(L+1)F + V_0 F = EF.\]
Una vez más, esta ecuación probablemente no te sea familiar, pero se puede refundir de una manera que la haga equivalente a la ecuación obedecida por las llamadas funciones esféricas de Bessel
\[ x^2\frac{d^2j_L(x)}{dx^2} +2x \frac{dj_L(x)}{dx} +[x^2 –L(L+1)] j_L(x) = 0\]
al tomar
\[x = \sqrt{\frac{2m(E-V_0)}{\hbar^2}} r.\]
El resultado es que las funciones de onda para este problema reducen a
\[\psi(r,\theta,\phi) = N Y_{L,M} (\theta,\phi) j_L\bigg(\sqrt{\frac{2m(E-V_0)}{\hbar^2}} r\bigg)\]
donde\(N\) es una constante de normalización. Las energías se determinan requiriendo\(\psi(r,\theta,\phi)\)
desaparecer en\(r = R\), lo que es análogo a insistir en que la función esférica de Bessel se desvanezca\(r = R\) en el problema anterior que estudiamos. Los valores de\(x (z_{L,n})\) a los que vuelven a\(j_L(x)\) desaparecer se pueden encontrar en diversas tabulaciones, entre ellas la citada anteriormente. Varios de estos valores se tabulan a continuación para ilustración.
Valores de\(x\) a los que se\(j_L(x)\) desvanecen para\(L = 0, 1, 2, 3\), y\(4\)
|
n=1 |
n=2 |
n=3 |
n=4 |
|
|---|---|---|---|---|
|
L=0 |
3.142 |
6.283 |
9.425 |
12.566 |
|
L=1 |
4.493 |
7.725 |
10.904 |
14.066 |
|
L=2 |
5.763 |
9.095 |
12.323 |
15.515 |
|
L=3 |
6.988 |
10.417 |
13.698 |
16.924 |
|
L=4 |
8.183 |
11.705 |
15.040 |
18.301 |
A partir de los valores de\(z_{L,n}\), se encuentran las energías de
\[E_{L,n} = V_0 + \frac{(z_{L,n})^2\hbar^2}{2mR^2}.\]
Nuevamente, vemos cómo la energía depende del tamaño de la región limitante (caracterizada por\(R\)) muy de la misma manera que en los sistemas anteriores. También vemos que\(E\) depende del número cuántico del momento angular\(L\) (tanto como lo hizo en el ejemplo anterior) y de la masa de la partícula. No obstante, el ordenamiento energético de estos niveles es diferente de lo que hemos visto anteriormente como se refleja en el ordenamiento de los\(z_{L,n}\) valores mostrados en la tabla anterior. Las energías aparecen en el orden (\(L=0\)\(n=1\);;\(L=-2\)\(n=1\);\(L=2\)\(n=1\);\(L=0\)\(n=2\);\(L=3\)\(n=1\);;\(L=1\)\(n=2\), y así sucesivamente, y esto es cierto para cualquier tamaño de esfera\(R\) y cualquier masa de partícula m.
Si, en lugar de estar restringida a moverse dentro de un volumen esférico, la partícula se restringe a moverse sobre la superficie de una esfera o radio\(R\), la variable\(R\) es fija (at\(R = R\)) y la ecuación de Schrödinger se convierte en
\[-\frac{\hbar^2}{2m} \frac{1}{R^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial\theta}\right) -\frac{\hbar^2}{2m}\frac{1}{R^2\sin^2\theta}\frac{\partial^2 \psi}{\partial\phi^2}+ V_0\psi = E\psi.\]
Usando
\[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial Y_{L,M}}{\partial\theta}\right)+ \frac{1}{\sin^2\theta}\frac{\partial^2 Y_{L,M}}{\partial\phi^2}= - L(L+1) Y_{L,M}.\]
podemos ver que las funciones de onda son los armónicos esféricos y las energías están dadas por
\[E_{L,M} = V_0 +\frac{L(L+1)\hbar^2}{2mR^2}\]
Tenga en cuenta que las energías dependen del número\(M\) cuántico\(L\) pero no del mismo. Entonces, cada estado que pertenece al nivel\(L\) es\(2L+1\) fold degenerado porque\(M\) va desde\(-L\) hasta\(L\).
Finalmente, si en lugar de estar obligada a moverse dentro de un círculo de radio R, la partícula se limitara a moverse sobre la superficie del círculo, la ecuación bidimensional de Schrödinger tratada anteriormente se reduciría a
\[- \frac{\hbar^2}{2mR^2} \frac{\partial^2\psi(\theta)}{\partial q^2} + V_0 \psi(\theta) = E\psi(\theta).\]
Las soluciones son las funciones familiares
\[\psi(\theta) = \sqrt{(1/2 \pi)} \exp(in\theta)\]
con\(n = 0, ±1, ±2, …\)
y las energías son
\[E_n = \frac{n^2 \hbar^2}{2mR^2} + V_0.\]
Obsérvese que la cuantificación de la energía surge porque el momento angular se cuantifica para ser\(nh\); esta condición surgió, a su vez, por la condición de que
\[\psi(\theta) = \psi(q +2\pi).\]
Al igual que en el caso de una partícula que se mueve dentro de la región circular, los estados con\(n > 0\) son doblemente degenerados; la diferencia entre pares de tales estados refleja el sentido de su momento angular.
Estos problemas de modelo se verán en el Capítulo 2 como representaciones muy útiles de situaciones que surgen cuando un electrón está constreñido dentro o sobre la superficie de diversas partículas nanoscópicas. Por ahora, se discutieron para ilustrar cómo las separaciones de variables a veces se pueden usar para descomponer la ecuación de Schrödinger en ecuaciones diferenciales ordinarias unidimensionales y para mostrar cómo son las condiciones límite (ya sea limitando\(y\) a desaparecer a ciertas distancias o insistiendo en que \(y\)ser periódicos cuando corresponda) que produzcan la cuantificación. Es importante señalar que es cuando una partícula está restringida espacialmente (por ejemplo, cuando su función de onda se vio obligada a desaparecer en dos ubicaciones\(x = 0\) y\(x = L_x\)) que se obtienen niveles de energía cuantificados. Cuando la partícula no está tan atrapada espacialmente, su energía no será cuantificada. Verá este comportamiento una y otra vez mientras exploramos otros modelos para movimientos electrónicos, vibracionales y rotacionales en moléculas.
La acción cuantificada también se puede utilizar para derivar niveles de energía
Hay otro enfoque que se puede utilizar para encontrar niveles de energía y es especialmente sencillo de usar para sistemas cuyas ecuaciones de Schrödinger son separables. La llamada acción clásica (denotada\(S\)) de una partícula que se mueve con impulso p a lo largo de una trayectoria que va desde la coordenada inicial\(q_i\) en el momento inicial\(t_i\) hasta una coordenada final\(q_f\) en el tiempo\(t_f\) se define por:
\[S = \int_{\textbf{q}_i;t_i}^{\textbf{q}_f;t_f}\textbf{p}\cdot\textbf{dq} .\]
Aquí, el vector de impulso p contiene el momento a lo largo de todas las coordenadas del sistema, y el vector de coordenadas\(q\) también contiene las coordenadas a lo largo de todos esos grados de libertad. Por ejemplo, en el problema bidimensional de partículas en una caja considerado anteriormente,\(\textbf{q} = (x, y)\) tiene dos componentes como lo hace\(\textbf{p} = (p_x, p_y)\), y la integral de acción es:
\[ S =\int_{x_i;y_i;t_i}^{x_f;y_f;t_f}(p_xdx+p_ydy).\]
Al computar tales acciones, es fundamental tener presente el signo del impulso a medida que la partícula se mueve desde sus posiciones iniciales a sus posiciones finales. Los ejemplos que se dan a continuación ayudarán a aclarar estos asuntos y mostrarán cómo aplicar la idea.
Para los sistemas para los que el hamiltoniano es separable, la integral de acción se descompone en una suma de tales integrales, una por cada grado de libertad. En el ejemplo bidimensional, la aditividad de H:
\[ H = H_x + H_y = \frac{p_x^2}{2m} + \frac{p_y^2}{2m} + V(x) + V(y)\]
\[ = - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + V(x) - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial y^2} + V(y)\]
significa que\(p_x\) y\(p_y\) puede resolverse independientemente en términos de los potenciales\(V(x)\) y así\(V(y)\) como de las energías\(E_x\) y\(E_y\) asociados con cada grado separado de libertad:
\[p_x = \pm\sqrt{2m(E_x-V(x))}\]
\[p_y = \pm\sqrt{2m(E_y-V(y))} ;\]
los signos\(p_x\) encendidos y\(p_y\) deben elegirse para reflejar adecuadamente el movimiento que la partícula está experimentando realmente en cualquier instante del tiempo. Sustituir estas expresiones en la integral de acción produce:
\[ S = S_x + S_y\]
\[= \int_{x_i;t_i}^{x_f;t_f} \pm\sqrt{2m(E_x-V(x))} dx + \int_{y_i;t_i}^{y_f;t_f} \pm\sqrt{2m(E_y-V(y))} dy.\]
Se ha demostrado que la relación entre estas integrales de acción clásicas y la existencia de niveles de energía cuantificados implica equiparar la acción clásica para el movimiento que es periódica entre un punto de inflexión izquierdo y derecho, como para una partícula clásica que experimenta un movimiento vibratorio periódico, a lo siguiente múltiplo de la constante de Planck:
\[S_{\text{closed}} = \int_{q_i;t_i}^{q_f;t_f} qdq= (n +\frac{1}{2}) h,\]
donde el índice de cuantificación\(n\) varía de 0 a\(\infty\) en pasos de unidad. Alternativamente, para el movimiento en una trayectoria angular cerrada, como para una partícula que se mueve en una trayectoria circular o elíptica, la condición de cuantificación de acción dice:
\[S_{\text{closed}} =\int_{q_i;t_i}^{q_f;t_f} pdq = nh,\]
donde de nuevo\(n\) va desde 0 hasta\(\infty\) en pasos de unidad.
Cuando se aplica acción-cuantificación como se describió anteriormente al llamado problema del oscilador armónico (esto sirve como el modelo razonable más simple para la vibración de una molécula diatómica AB) que estudiaremos en forma cuántica más adelante, se expresa la energía total como la suma de energías cinéticas y potenciales
\[E = \frac{p^2}{2m} + \frac{k}{2} x^2\]
donde\[m = \dfrac{m_Am_B}{m_A + m_B}\] es la masa reducida de la molécula diatómica AB,\(k\) es la constante de fuerza que describe el enlace entre A y B,\(x\) es el desplazamiento de la longitud del enlace y p es el momento asociado con la longitud del enlace. El requisito de acción cuantificada luego lee
\[(n +\frac{1}{2}) h = \int p dx = \int \sqrt{2\mu(E-k/2 x^2)} dx.\]
Esta integral se lleva a cabo entre\(x = - \sqrt{2E/k}\) y\(\sqrt{2E/k}\) los puntos de inflexión izquierdo y derecho del movimiento oscilatorio y de nuevo para formar una trayectoria cerrada. Llevar a cabo esta integral y equipararla\((n +\frac{1}{2}) h\) da la siguiente expresión para la energía\(E\):
\[E = (n +\frac{1}{2}) (\hbar^2\pi) \sqrt{\dfrac{k}{\mu}} .\]
Si\(n\) se permite que el número cuántico asuma valores enteros que van desde\(n = 0\), 1, 2, hasta el infinito, estos niveles de energía concuerdan con los resultados del tratamiento cuántico completo que obtendremos posteriormente.
Para un ejemplo de aplicar este enfoque a un problema que involucra movimiento a lo largo de un bucle cerrado, consideremos la rotación libre (es decir, sin potencial que afecte su movimiento angular) de una molécula diatómica AB que tiene una longitud de enlace fija R. La energía rotacional puede escribirse como
\[E=\frac{p_\phi^2}{2\mu R^2}\]
donde es el momento asociado con la rotación y\(m\) es la masa reducida de la molécula AB. Resolver e insertar esto en la ecuación de acción-cuantificación apropiada para el movimiento a lo largo de un bucle cerrado da
\[\int_{\phi=0}^{\phi=2\pi} p_\phi d\phi=\int_{\phi=0}^{\phi=2\pi} \sqrt{2\mu R^2E} d\phi = \sqrt{2\mu R^2 E}(2\pi) = nh.\]
Resolviendo para la energía\(E\) luego da
\[E=\frac{(nh)^2}{(2\pi)^22\mu R^2}=\frac{n^2h^2}{2\mu R^2},\]
que es exactamente el mismo resultado que obtuvimos antes al resolver la ecuación de Schrödinger para el movimiento de una partícula que se mueve sobre un círculo.
Ahora, vamos a aplicar la cuantificación de acción a cada una de las coordenadas independientes de la partícula bidimensional en un problema de caja. Las dos condiciones de cuantificación de acción separadas dicen:
\[\big(n_x +\dfrac{1}{2}\big) h =\int_{x=0}^{x=L_x} \sqrt{2m(E_x-V(x))} dx +\int_{x=L_x}^{x=0} -\sqrt{2m(E_x-V(x))} dx \]
\[ (n_y +\dfrac{1}{2}) h = \int_{y=0}^{y=L_y} \sqrt{2m(E_y-V(y))} dy +\int_{y=L_y}^{y=0} -\sqrt{2m(E_y-V(y))} dy .\]
Observe que los signos de los momentos son positivos en cada una de las primeras integrales que aparecen arriba (porque la partícula se mueve de\(x = 0\) a\(x = L_x\), y análogamente para\(y\) -movimiento, y por lo tanto tiene impulso positivo) y negativo en cada una de las segundas integrales (porque el movimiento es de \(x = L_x\)a\(x = 0\) (y análogamente para\(y\) -movimiento) y así la partícula tiene un impulso negativo). Dentro de la región delimitada por\(0 \le x\le L_x; 0 \le y\le L_y\), el potencial es constante y puede tomarse como cero (esto solo da nuestro punto de referencia para la energía total). Utilizando este hecho, e invirtiendo los límites superior e inferior, y así el signo, en las segundas integrales anteriores, se obtiene:
\[\big(n_x +\dfrac{1}{2}\big) h = 2\int_{x=0}^{x=L_x} \sqrt{2mE_x} dx= 2\sqrt{2mE_x} L_x\]
\[\big(n_y +\dfrac{1}{2}\big) h = 2\int_{y=0}^{y=L_y} \sqrt{2mE_y} dy= 2\sqrt{2mE_y} L_y.\]
Resolviendo para\(E_x\) y\(E_y\), uno encuentra:
\[E_x =\frac{[\big(n_x +\dfrac{1}{2}\big)h]^2}{8mL_x^2}\]
\[E_y =\frac{[\big(n_y +\dfrac{1}{2}\big)h]^2}{8mL_y^2} .\]
Estos no son los mismos niveles de energía cuantificados que surgieron cuando las condiciones de límite de la función de onda coincidieron en\(x = 0\),\(x = L_x\) y\(y = 0\),\(y = L_y\). En el enfoque de la ecuación de Schrödinger, las expresiones energéticas no tenían el\(\dfrac{1}{2}\) factor + que aparece en el resultado anterior basado en la acción. Resulta que, para potenciales que se definen de manera fragmentada, como es el potencial de partícula en una caja (es decir, el potencial sufre un salto infinito en\(x = 0\) y\(x = L\)), la condición de cuantificación de acción tiene que ser modificada. Un ejemplo de cómo y por qué hay que hacer esta modificación se da en un artículo del grupo del Prof. Bill Miller (J. E. Adams y W. H. Miller, J. Chem. Phys. 67, 5775-5778 (1977)), pero no voy a discutirlo más aquí porque sus detalles están más allá del nivel de este texto. Baste decir que para el movimiento periódico entre dos puntos de inflexión en un potencial suave (es decir, no por partes),\((n+\dfrac{1}{2})h\) es el valor de cuantificación de acción correcto. Para el movimiento angular en un bucle cerrado, nh es el valor adecuado. Pero, para el movimiento periódico entre puntos de inflexión sobre un potencial por partes, las modificaciones discutidas en la referencia anterior deben aplicarse para hacer que la cuantificación de acciones reproduzca el resultado cuántico correcto.
El uso de la cuantificación de acciones como se ha ilustrado anteriormente se ha convertido en una herramienta muy importante. Ha permitido a los científicos hacer grandes avances para cerrar la brecha entre las descripciones clásicas y cuánticas de la dinámica molecular. En particular, mediante el uso de conceptos clásicos como trayectorias y luego imponiendo condiciones de acción cuantificada, las personas han podido desarrollar los llamados modelos semi-clásicos de dinámica molecular. En tales modelos, uno es capaz de retener una gran cantidad de comprensión clásica mientras se construyen efectos cuánticos como la cuantificación de energía, las energías de punto cero y las interferencias. Tanto en el sitio web de My Theory Page como a partir de artículos a los que se accede en el sitio web del profesor William H. Miller, uno de los pioneros de la teoría semi-clásica aplicada a la química, se puede conocer más sobre este tema.
Antes de salir de esta sección, vale la pena discutir un poco más la cuantificación de energía y momento angular que se produce al tratar el movimiento rotacional unidimensional libre de una partícula en un círculo o una molécula rígida lineal restringida a acostarse sobre un plano. Cuando usamos la cuantificación de acciones para abordar este tipo de problema, obtuvimos energías cuantificadas
\[E=\frac{n^2h^2}{2\mu R^2}\]
que, a través de la expresión energética dada en términos de momento angular
\[E=\frac{p_\phi^2}{2\mu R^2},\]
implica que el momento angular en sí está cuantificado
\[p_\phi=\pm nh.\]
Este es el mismo resultado que obtenemos cuando buscamos funciones propias y valores propios del operador de momento\(\textbf{L}_z\) angular de mecánica cuántica. Como mostramos anteriormente, este operador, cuando se calcula como el\(z\) -componente de\(\textbf{R} \times \textbf{p}\), puede escribirse en\((r, \theta, \phi)\) coordenadas polares como
\[L_z = - i \hbar \dfrac{d}{d\phi}.\]
Las funciones propias de este operador tienen la forma\(\exp(ia\phi)\), y los valores propios son a h. Debido a que las geometrías con ángulos azimutales iguales\(\phi\) o iguales a\(\phi + 2\pi\) son exactamente las mismas geometrías, la función\(\exp(ia\phi)\) debe ser exactamente la misma que\(\exp(ia(\phi+2\pi))\). Este solo puede ser el caso si a es un entero. Así, se concluye que solo se pueden permitir múltiplos integrales de h valores de la\(z\) -componente del momento angular.
Experimentalmente, se mide el\(z\) componente de un momento angular colocando el sistema que posee el momento angular en un campo magnético de fuerza B y observando cuántos estados\(z\) de energía de componentes surgen. Esta división en los niveles de energía se denomina el efecto Zeeman. Por ejemplo, un átomo de boro con un electrón desapareado su\(2\pi\) orbital tiene una unidad de momento angular orbital, por lo que se encuentran tres valores\(z\) de componentes separados que generalmente se denotan\(m = -1, m=0,\) y\(m=1\). Otro ejemplo lo ofrece el átomo de escandio con un electrón desapareado en un orbital d; los estados de este átomo se dividen en estados\(z\) de cinco (\(m = -2, -1, 0, 1, 2\)) componentes. En cada caso, se encuentran\(2L + 1\) valores del número\(m\) cuántico, y, debido a que L es un entero,\(2L + 1\) es un entero impar. Ambas observaciones son consistentes con la expectativa de que solo pueden ocurrir valores enteros para los\(L_z\) valores propios obtenidos de la cuantificación de acciones y de la condición de límite\(\exp(ia\phi) = \exp(ia(\phi+2\pi))\).
Sin embargo, se ha observado que algunas especies no poseen 3 o 5 o 7 o 9 estados\(z\) componentes sino un número par de dichos estados. En particular, se observa que los electrones, protones o neutrones solo tienen valores propios\(z\) de dos componentes. Esto también se observa en, por ejemplo, el átomo de boro mencionado anteriormente, si se examinan las divisiones adicionales de los niveles\(2\pi\) (m = -1, 0 y 1) causadas por la acción del campo magnético sobre el espín del electrón desapareado. Porque, como discutimos más adelante en este texto, todos los momentos angulares tienen valores propios\(z\) -componentes que están separados entre sí por múltiplos unitarios de h, uno se ve obligado a concluir que estas tres partículas fundamentales del bloque de construcción (electrones, protones y neutrones) tienen\(z\) -componente valores propios de\(\dfrac{1}{2} \hbar\) y\(-\dfrac{1}{2} \hbar\). La aparición de momentos angulares semiintegrales no es consistente con el resultado de acción-cuantificación o la observación realizada anteriormente\(\phi\) y\(\phi + 2\pi\) corresponden exactamente al mismo punto físico en el espacio de coordenadas, lo que, a su vez, implica que solo son posibles los momentos angulares enteros completos.
La resolución de la paradoja anterior (es decir, ¿cómo pueden existir momentos angulares de medio entero?) implica darse cuenta de que algunos momentos angulares no corresponden al momento\(\textbf{R} \times \textbf{p}\) angular de una masa física que gira, sino que, en cambio, son propiedades intrínsecas de ciertas partículas. Es decir, el momento angular intrínseco de electrones, protones y neutrones no puede ser visto como derivado de la rotación de alguna masa que comprende estas partículas. En cambio, tales momentos angulares intrínsecos son fundamentales construidos en las características de estas partículas. Por ejemplo, los estados de impulso dos\(\dfrac{1}{2} \hbar\) y\(-\dfrac{1}{2} \hbar\) angular de un electrón, generalmente denotados a y b, respectivamente, son dos estados internos del electrón que son degenerados en ausencia de un campo magnético pero que representan dos estados distintos del electrón. Análogamente, un protón tiene\(\dfrac{1}{2} \hbar\) y\(-\dfrac{1}{2} \hbar\) afirma, al igual que los neutrones. Todos estos estados de momento angular semiintegrales no pueden contabilizarse utilizando la mecánica clásica, sino que se sabe que surgen en la mecánica cuántica. Esto quiere decir que, cuando enseñamos química introductoria a estudiantes jóvenes, no es correcto decir que los estados de espín arriba y abajo (a y b) de un electrón pueden verse en términos de la masa del electrón girando en sentido horario o antihorario alrededor de algún eje. Dichos momentos angulares de masa giratoria solo pueden poseer valores enteros; los momentos angulares de medio entero no pueden y no deben describirse en términos de masas giratorias.
La acción también se puede utilizar para generar funciones de onda
Las integrales de acción calculadas a partir de descripciones clásicas de movimiento en superficies de energía potencial también se pueden usar para generar funciones de onda cuántica aproximadas. Hacerlo ofrece otra vía más para hacer conexión entre los mundos clásico y cuántico. Para ver cómo tal conexión puede surgir directamente de la ecuación de Schrödinger, comenzamos con la ecuación de Schrödinger independiente del tiempo para una sola partícula de masa que\(m\) se mueve sobre un potencial\(V(r)\) que depende de las coordenadas de posición de la partícula\(r\):
\[E\Psi(r)=-\frac{\hbar^2}{2m}\nabla^2\Psi(r)+V(r)\Psi(r).\]
Entonces, expresamos la función de onda compleja como una amplitud real constante A multiplicada por una fase compleja que escribimos como:
\[\Psi(r)=A\exp(iW(r)/\hbar).\]
Sustituir esta expresión por en la ecuación de Schrödinger da una ecuación para\(W\):
\[E=V+\frac{(\nabla W)^2}{2m}-i\hbar\frac{\nabla^2W}{2m}.\]
Esta ecuación contiene componentes tanto reales como imaginarios (n.b.,\(W\) en sí es complejo). Por lo general, se resuelve asumiendo que se\(W(r)\) puede expandir en una serie de potencias en la variable\(\hbar\). Esta expansión está motivada por señalar que si se descuida el\(\dfrac{\nabla^2 W}{2m}i\hbar\) factor en la ecuación anterior, la ecuación resultante
\[0=V-E+\frac{(\nabla W)^2}{2m}\]
tendría sentido si\(\nabla W(r)\) fueran iguales al impulso clásico de la partícula. Entonces, tomar el\(\hbar\rightarrow 0\) límite de la ecuación para\(W(r)\) parece reducir esta ecuación de mecánica cuántica a un resultado clásico en el que\(\nabla W(r) = p(r)\).
Entonces, sustituyendo
\[W(r)=W_0(r)+hW_1(r)+\hbar^2W_2(r)+\cdots\]
en la ecuación anterior para\(W(r)\) y reuniendo todos los términos de un poder dado en produce ecuaciones para los diversos\(W_n(r)\), los dos primeros de los cuales dicen:
\[0=2m(V-E)+(\nabla W_0)^2\]
y
\[0=2\nabla W_0\cdot \nabla W_1-i\nabla^2 W_0.\]
Para simplificar más la discusión de esta llamada teoría semiclásica de la función de onda, limitemos la atención al caso en el que solo hay una coordenada espacial. Para los casos bidimensionales o tridimensionales,\(\nabla W_0\) y\(\nabla W_1\) son cantidades vectoriales, y la solución de estas ecuaciones es considerablemente más complicada, sobre todo si el potencial no se\(V(\textbf{r})\) puede separar en contribuciones aditivas de cada una de las variables. Cuando sólo hay una coordenada espacial, y son cantidades escalares.
La primera ecuación se puede resolver\(W_0(r)\) y da dos soluciones independientes (es decir, las correspondientes al signo ±):
\[W_0(r)=\pm\int\sqrt{2m(E-V(r^\prime))dr^\prime},\]
cada uno de los cuales será real cuando\(E > V(r)\) (es decir, en regiones del espacio clásicamente permitidas) e imaginario cuándo\(E < V(r)\) (es decir, en regiones clásicamente prohibidas). Observe que\(W_0(r)\) contiene un integrando igual al impulso clásico\(p(r)=\sqrt{2m(E-V(r)) }\).
La ecuación para también se\(W_1(r)\) puede resolver:
\[W_1(r)=\frac{i}{2}\ln[\sqrt{2m(E-V(r))}].\]
Entonces, a través de primer orden en\(\hbar\), las funciones de onda semi-clásicas son
\[\Psi(r)=A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\exp\left(\frac{i\hbar}{2h}i\ln[\sqrt{2m(E-V(r))}]\right).\]
\[=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\]
Estos pares de funciones de onda a menudo se expresan como
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\]
en regiones del espacio donde\(E > V\), y
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right)\]
en las regiones clásicamente prohibidas donde\(V > E\). Observe que las funciones de onda en las regiones clásicamente permitidas tienen densidades de probabilidad dadas por
\[\Psi^*\Psi=\frac{A^2}{\sqrt{2m(E-V(r))}}\]
que es exactamente la densidad de probabilidad clásica que discutimos anteriormente en este Capítulo. La probabilidad es inversamente proporcional a la velocidad de la partícula en la ubicación r, y tiene la misma singularidad que la probabilidad clásica en los puntos de inflexión (donde\(V = E\)). En contraste, las densidades de probabilidad en regiones donde crecen\(V > E\) o decaen exponencialmente dentro de estas regiones clásicamente prohibidas.
Veamos cómo estas funciones de onda semi-clásicas se pueden aplicar a algunos de los problemas del modelo que discutimos anteriormente. Para el problema unidimensional de partículas en caja, las dos funciones de crecimiento exponencial y descomposición no son necesarias porque en las regiones\(R < 0\) y\(R > L\), la función de onda se puede tomar para desaparecer. Dentro de la región\(0 \le r \le L\), hay dos funciones de onda independientes
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right),\]
y el potencial\(V(r’)\) es constante (llamemos al potencial en esta región\(V_0\)). Entonces, la integración que aparece en estas dos funciones de onda se puede llevar a cabo para dar
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right).\]
Podemos combinar estas dos funciones para generar una función que desaparecerá en\(R = 0\) (como debe para este problema de partículas en una caja):
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\left[\exp\left(\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right)-\exp\left(-\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right)\right].\]
Entonces podemos usar la condición que también\(\Psi\) debe desaparecer en\(R = L\) para obtener una ecuación que especifique las energías\(E\) que están permitidas:
\[0=\left[\exp\left(\frac{iL}{\hbar}\sqrt{2m(E-V_0)}\right)-\exp\left(-\frac{iL}{\hbar}\sqrt{2m(E-V_0)}\right)\right]=2i\sin\left(\frac{L}{\hbar}\sqrt{2m(E-V_0)}\right),\]
lo que significa que
\[E=V_0+\frac{n^2\pi^2\hbar^2}{2mL^2}.\]
Estas energías son exactamente las mismas que encontramos cuando resolvimos la ecuación de Schrödinger para este problema de modelo.
Es informativo señalar que estas funciones de onda semi-clásicas, que no son exactas porque se obtuvieron al retener solo términos hasta la primera potencia de\(\hbar\), fueron capaces de generar patrones nodales cuánticos (es decir, interferencias) y niveles de energía cuantificados a pesar de que contenían clásicos conceptos como el impulso en diversas posiciones en el espacio. Fue superponiendo dos funciones que tienen la misma energía que se obtuvieron patrones nodales.
Consideremos ahora qué sucede cuando aplicamos la función de onda semi-clásica al problema del oscilador armónico también discutido anteriormente. En este caso, hay dos puntos de inflexión clásicos\(r_1\) y\(r_2\) en los que\(E = V(r)\). Las funciones de onda semi-clásicas apropiadas a las tres regiones (dos clásicamente prohibidas y una clásicamente permitida) son:
\[\Psi_1=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A_1\exp\left(-\frac{1}{\hbar}\int_{r_2}^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right),r\ge r_2.\]
\[\Psi_2=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A_2\exp\left(\frac{1}{\hbar}\int_{r_1}^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right),r\le r_1.\]
\[\Psi_3=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}\left[A_3\exp\left(\frac{i}{\hbar}\int_{r_1}^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)-A_{3^\prime}\exp\left(-\frac{i}{\hbar}\int_{r}^{r_2}\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\right],r_1\le r\le r_2.\]
Las dos primeras se descomponen exponencialmente dentro de las dos regiones clásicamente prohibidas. La tercera es una combinación de las dos soluciones independientes dentro de la región clásicamente permitida, con las amplitudes de las dos soluciones definidas por los coeficientes\(A_3\) y\(A_{3’}\). Las amplitudes\(A_1\) y\(A_2\) multiplicar las funciones de onda en las dos regiones clásicamente prohibidas, y las cuatro amplitudes así como la energía\(E\) deben determinarse (i) normalizando la función de onda total para obedecer
\[\int_{-\infty}^{\infty}\Psi^*\Psi dr=1\]
y (2) haciendo coincidir las funciones de onda\(\Psi_1\) y\(\Psi_3\) y sus primeras derivadas en\(R = r_1\), y las funciones de onda\(\Psi_2\) y\(\Psi_3\) y sus primeras derivadas en\(R = r_2\).
Antes de abordar cómo se podría lograr esta coincidencia de función de onda, permítanme señalar una propiedad interesante del factor que entra en el exponencial de la función de onda semi-clásica. Primero usamos las dos expresiones
\[\frac{dW_0}{dr}=\pm\sqrt{2m(E-V(r))} \]
y
\[\frac{dW_1}{dr}=\dfrac{i\dfrac{d\sqrt{2m(E-V)}}{dr}}{2\sqrt{2m(E-V)}}\]
dado anteriormente para los dos primeros componentes de\(W(r)\) y luego hacer uso de la forma armónica de\(V(r)\)
\[V(r)=\frac{1}{2}kr^2.\]
A continuación, evaluamos la integral de\(\dfrac{dW}{dr}\) para un camino clásico cerrado en el que el sistema se mueve desde el punto de inflexión izquierdo
\[r_1=-\sqrt{\frac{2E}{k}}\]
al punto de inflexión derecho
\[r_2=\sqrt{\frac{2E}{k}}\]
y de nuevo a la izquierda punto de inflexión. La contribución de la integración\(\dfrac{dW_0}{dr}\) a lo largo de este camino cerrado es (n.b., el signo + se usa para la primera parte del camino porque la partícula tiene impulso positivo, y el signo — se aplica a la parte de retorno del camino cuando la partícula tiene impulso negativo):
\[W_0=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr\]
que es exactamente la integral de acción que tratamos anteriormente en este Capítulo cuando calculamos para el oscilador armónico clásico. La contribución de la integración\(\dfrac{dW_1}{dr}\) a lo largo de este camino cerrado se puede evaluar escribiendo primero
\[\frac{dW_1}{dr}=\dfrac{i\dfrac{d\sqrt{2m(E-1/2 kr^2)}}{dr}}{2\sqrt{2m(E-1/2 kr^2)}}=\frac{-ikr}{4(E-1/2 kr^2)}.\]
La integral de\(r_1\) a\(r_2\) de esta cantidad se puede llevar a cabo (utilizando la sustitución\(r = \sqrt{2E/k} y\)) como
\[\dfrac{-ik}{4}\int_{-\sqrt{2E/k}}^{\sqrt{2E/k}}\dfrac{rdr}{(E-1/2kr^2)}=\dfrac{-ik}{4}\int_{-1}^{1}\dfrac{\dfrac{2E}{k}ydy}{E(1-y^2)}=\dfrac{-i}{4}\int_{-1}^{1}\dfrac{ydy}{(1-y)(1+y)}.\]
La evaluación de la integral restante en el lado derecho se puede hacer utilizando la integración de contornos (los estudiantes de pregrado pueden no haber encontrado esta materia dentro de la teoría de variables complejas; los remito a pp. 367-377 Methods of Theoreical Physics, P. M. Morse y H. Feshabach, McGraw-Hill, Nueva York (1953) o p. 113 Variables Complejas Aplicadas, J. W. Dettman, Macmillan Co. Nueva York (1965)). La ecuación básica de la integración de contorno dice que una integral de la forma\(\int \dfrac{f(z)}{(z-a)}dz\), donde\(z = a\) es una singularidad, es igual a\(2\pi if(a)\). Nuestra integral tiene singularidades en\(y = 1\) y en\(y = -1\), por lo tanto, hay dos de esas contribuciones. El resultado neto es que nuestra integral reduce a
\[\frac{-i}{4}\int_{-1}^{1}\frac{ydy}{(1-y)(1+y)}=\frac{i}{4}2\pi i\left[\frac{1}{2}+\frac{-1}{-2}\right]=-\frac{\pi}{2}.\]
Entonces, la contribución a la integral de\(\dfrac{dW_1}{dr}\)\(r_1\) derivar de a\(r_2\) es igual a\(–\pi/2\). La integral de\(r_2\) atrás a\(r_1\) da otro factor o\(–\dfrac{\pi}{2}\). Combinar la integral de\(\dfrac{dW_0}{dr}\) y la integral de\(\dfrac{dW_1}{dr}\) (multiplicada por porque\(W = W_0 + \hbar W_1 + …\)) da el siguiente resultado final
\[W=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\pi \hbar\]
Si la cuantificación original de Bohr se aplica a la integral de a\(\dfrac{dW}{dr}\) lo largo de un camino clásico cerrado:
\[W=nh,n=1,2,3,\cdots\]
nuestro resultado anterior dice entonces que
\[nh=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\frac{1}{2}h\]
que es lo mismo que
\[\int p(r)dr=\big(n+\dfrac{1}{2}\big)h.\]
Esto significa que el\(\dfrac{1}{2}\) factor que surge en la condición de cuantificación de acción para movimientos periódicos entre dos puntos de inflexión puede ser visto como derivado de la primera corrección cuántica (es decir, el término primer orden en\(\hbar\)) a la función de onda semi-clásica. Recordemos que igualando esta acción clásica integral\(\big(n+\dfrac{1}{2}\big) h\) dio las energías correctas (es decir, cuánticas) para este problema del oscilador armónico.
Hemos visto cómo se puede definir una función de onda semi-clásica, cuál es su densidad de probabilidad espacial, cómo se puede construir en interferencia (para lograr patrones nodales adecuados) y cómo cuantificar su acción puede dar los niveles de energía permitidos correctos. No obstante, hay un tema que no hemos abordado completamente. Para resolver los coeficientes que\((A_1, … A_{3’})\) multiplican las funciones de onda semi-clásicas en las regiones clásicamente permitidas y prohibidas, las funciones de onda\(\Psi_1\)\(\Psi_3\) y sus primeras derivadas deben coincidir en\(r = r_1\), y las funciones de onda\(\Psi_2\) y\(\Psi_3\) y su primera los derivados deben coincidir en\(R\) =\(r_2\). Desafortunadamente, los detalles de este proceso de emparejamiento son bastante complicados y requieren examinar con más detalle la naturaleza de las funciones de onda cerca de los puntos de inflexión clásicos donde cada uno de\(\Psi_1\)\(\Psi_2\),, y\(\Psi_3\) contienen factores de la forma\(\sqrt{\sqrt{2m(-E+V(r)}}\) en sus denominadores. Debe quedar claro que las funciones coincidentes y sus derivadas que contienen tales singularidades plantean retos especiales. No voy a ir más allá en este asunto aquí; más bien, remito al lector interesado a las pp. 268-279 de Quantum Mechanics, 3rd Ed., L. I. Schiff, McGraw-Hill, Nueva York (1968) para un buen tratamiento de este llamado enfoque WKB al tema de emparejamiento.
Colaboradores y Atribuciones
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


