1.3: La aproximación Nacido-Oppenheimer

Una de las aproximaciones más importantes relacionadas con la aplicación de la mecánica cuántica a moléculas e iones moleculares se conoce como la aproximación Born-Oppenheimer (BO). La idea básica detrás de esta aproximación implica darse cuenta de que en el operador Hamiltoniano lleno de electrones más-núcleos introducido anteriormente

\[H = \sum_i \left[- \dfrac{\hbar^2}{2m_e} \dfrac{\partial^2}{\partial q_i^2} \right]+ \dfrac{1}{2} \sum_{j\ne i} \dfrac{e^2}{r_{i,j}} - \sum_{a,i} \dfrac{​Z_ae^2}{r_{i,a}} + \sum_a \left[- \dfrac{\hbar^2}{2m_a} \dfrac{\partial^2}{\partial q_a^2}\right]+ \dfrac{1}{2} \sum_{b\ne a} \dfrac{​Z_aZ_b e^2}{r_{a,b}} \]

las escalas de tiempo con las que se mueven los electrones y los núcleos suelen ser bastante diferentes. En particular, los núcleos pesados (es decir, incluso un núcleo H pesa casi 2000 veces lo que pesa un electrón) se mueven (es decir, vibran y giran) más lentamente que los electrones más ligeros. Por ejemplo, los movimientos vibracionales de enlace típicos ocurren en escalas de tiempo de ca.\(10^{-14}\) s, las rotaciones moleculares requieren\(10^{-100}\) tiempos tan largos, pero los electrones experimentan movimientos periódicos dentro de sus órbitas en la escala de tiempo\(10^{-17}\) s si residen dentro de orbitales centrales o de valencia. Así, esperamos que los electrones puedan “ajustar” rápidamente sus movimientos a los núcleos que se mueven mucho más lentamente.

Esta observación nos motiva a considerar resolver la ecuación de Schrödinger para el movimiento de los electrones en presencia de núcleos fijos como una forma de representar el estado completamente ajustado de los electrones en cualquier posición fija de los núcleos. Por supuesto, entonces tenemos que tener una manera de describir las diferencias entre cómo se comportan los electrones y los núcleos en ausencia de esta aproximación y cómo se mueven dentro de la aproximación. Estas diferencias dan lugar a las llamadas correcciones no nacidas en Oppenheimer, transiciones sin radiación, saltos superficiales y transiciones no adiabáticas, que trataremos más adelante.

Cabe señalar que esta separación de escalas de tiempo entre movimientos electrónicos rápidos y lentos de vibración y rotación no se aplica tan bien a, por ejemplo, los estados Rydberg de átomos y moléculas. Como se discutió anteriormente, en tales estados, el electrón en la órbita de Rydberg tiene una velocidad mucho menor y una extensión radial mucho mayor que para los orbitales típicos de núcleo o valencia. Por esta razón, las correcciones al modelo BO suelen ser más importantes de hacer al tratar con los estados de Rydberg.

El Hamiltoniano electrónico que pertenece a los movimientos de los electrones en presencia de núcleos sujetos

\[H = \sum_i \left[- \dfrac{\hbar^2}{2m_e} \dfrac{\partial^2}{\partial q_i^2} \right]+ \dfrac{1}{2} \sum_{j\ne i} \dfrac{e^2}{r_{i,j}} - \sum_{a,i} \dfrac{​Z_ae^2}{r_{i,a}} \dfrac{1}{2} \sum_{b\ne a} \dfrac{​Z_a Z_b e^2}{r_{a,b}}\]

produce como sus valores propios a través de la ecuación

\[H \psi_J(q_j|q_a) = E_J (q_a) \psi_J(q_j|q_a)\]

energías\(E_K (q_a)\) que dependen de donde se localicen los núcleos (es decir, las {\(q_a\)} coordenadas). Como sus funciones propias, se obtiene lo que se denominan funciones de onda electrónica {\(\psi_K(q_i|q_a)\)} que también dependen de dónde se localicen los núcleos. Las energías\(E_K(q_a)\) son lo que solemos llamar superficies energéticas potenciales. Un ejemplo de dicha superficie se muestra en la Figura 1.5.

Figura 1.5. Superficie de energía potencial bidimensional que muestra mínimos locales, estados de transición y caminos que los conectan.

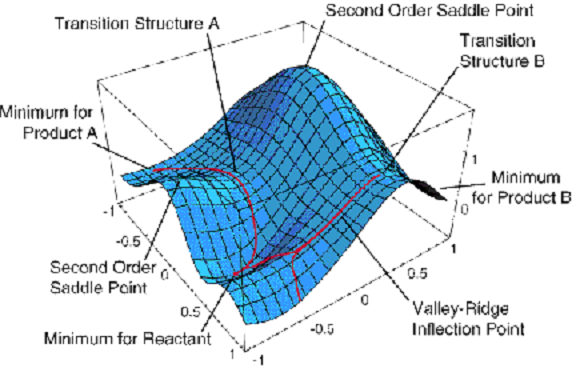
Esta superficie depende de dos coordenadas geométricas\(\{q_a\}\) y es una gráfica de un valor propio en particular\(E_J(q_a)\) frente a estas dos coordenadas.

Si bien esta trama tiene más información sobre ella de la que discutiremos ahora, vale la pena señalar algunas características. Parecen haber tres mínimos (es decir, puntos donde la derivada de\(E_J\) con respecto a ambas coordenadas desaparece y donde la superficie tiene curvatura positiva). Estos puntos corresponden, como veremos hacia el final de este material introductorio, a geometrías de estructuras moleculares estables. La superficie también muestra dos puntos de sillín de primer orden (etiquetados como estructuras de transición A y B) que conectan los tres mínimos. Estos puntos tienen cero primera derivada de\(E_J\) con respecto a ambas coordenadas pero tienen una dirección de curvatura negativa. Como veremos más adelante, estos puntos describen estados de transición que juegan un papel crucial en la cinética de las transiciones entre las tres geometrías estables.

Tenga en cuenta que la Figura 1.5 muestra solo una de las\(E_J\) superficies; cada molécula tiene una superficie en estado fundamental (es decir, la que es la que es más baja en energía) así como un número infinito de superficies en estado excitado. Volvamos ahora a nuestra discusión sobre el modelo BO y preguntemos qué se hace una vez que se tiene esa superficie energética en la mano.

Posteriormente se supone que el movimiento de los núcleos, dentro del modelo BO, obedece a una ecuación de Schrödinger en la que

\[\displaystyle\sum_a [- \dfrac{\hbar^2}{2m_a} \dfrac{\partial^2}{\partial q_a^2} ]+ \dfrac{1}{2} \sum_{b\ne a} \dfrac{Z_aZ_be^2}{r_{a,b}} + E_K(q_a)\]

define un hamiltoniano de rotación-vibración para el estado energético particular\(E_K\) de interés. Las energías rotacionales y vibracionales y las funciones de onda pertenecientes a cada estado electrónico (es decir, para cada valor del índice\(K\) en\(E_K(q_a)\)) se encuentran luego resolviendo un\(E_K\) hamiltoniano.

Este modelo de BO forma la base de gran parte de cómo los químicos ven la estructura molecular y la espectroscopia molecular. Por ejemplo, aplicado al formaldehído\(H_2C=O\), hablamos del estado electrónico de tierra singlete (con todos los electrones emparejados y ocupando los orbitales de menor energía) y sus estados vibracionales y rotacionales así como los estados\(n\rightarrow \pi^*\) y\(\pi\rightarrow \pi^*\) electrónicos y sus vibraciones y rotacionales niveles. Si bien se dirá mucho más sobre estos conceptos más adelante en este texto, el estudiante debe estar al tanto de los conceptos de superficies de energía electrónica (es decir, el {\(E_K(q_a)\)}) y los estados de vibración-rotación que pertenecen a cada una de esas superficies.

Debo señalar que las coordenadas\(3N\) cartesianas {\(q_a\)} utilizadas para describir las posiciones de los\(N\) núcleos de la molécula pueden ser reemplazadas por 3 coordenadas cartesianas\((X,Y,Z)\) especificando el centro de masa de los\(N\) núcleos y\(3N-3\) otras llamadas coordenadas internas que se puede usar para describir la orientación de la molécula (estas coordenadas aparecen en la energía cinética rotacional) y sus longitudes y ángulos de enlace (estas coordenadas aparecen en las energías cinéticas vibracionales y potenciales). Cuando se utilizan coordenadas centrales e internas en lugar de las coordenadas\(3N\) cartesianas, se ve que las superficies de energía Born-Oppenheimer {\(E_K(q_a)\)} dependen únicamente de las coordenadas internas. Además, si la energía de la molécula no depende de su orientación (por ejemplo, si se mueve libremente en la fase gaseosa), la {\(E_K(q_a)\)} tampoco dependerá de las 3 coordenadas orientacionales, sino solo de las coordenadas\(3N-6\) vibracionales.

Habiendo sido introducidos a los conceptos de operadores, funciones de onda, el hamiltoniano y su ecuación de Schrödinger, es importante considerar ahora varios ejemplos de las aplicaciones de estos conceptos. Los ejemplos tratados a continuación fueron elegidos para proporcionar al lector una valiosa experiencia en la resolución de la ecuación de Schrödinger; también se eligieron porque forman los modelos químicos más elementales de movimientos electrónicos en moléculas conjugadas y en átomos, rotaciones de moléculas lineales y vibraciones de enlaces químicos.

Su Primera Aplicación de Mecánica Cuántica- Movimiento de una Partícula en una Dimensión

Este es un problema muy importante cuyas soluciones utilizan los químicos para modelar una amplia variedad de fenómenos.

Comencemos examinando el movimiento de una sola partícula de masa\(m\) en una dirección a la que llamaremos\(x\) bajo la influencia de un potencial denotado\(V(x)\). La expresión clásica para la energía total de dicho sistema es\(E = \dfrac{p^2}{2m} + V(x)\), donde\(p\) está el impulso de la partícula a lo largo del eje x. Para enfocarse en ejemplos específicos, considere cómo se movería esta partícula si\(V(x)\) fuera de las formas mostradas en la Figura 1. 6, donde la energía total\(E\) se denota por la posición de la línea horizontal.

Figura 1. 6. Tres potenciales característicos que muestran puntos de inflexión clásicos izquierdo y derecho en energías denotadas por las líneas horizontales.

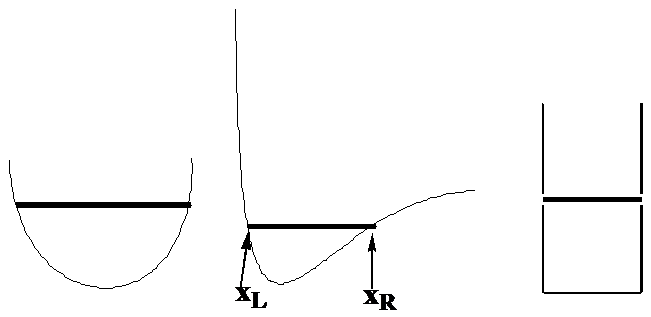
La densidad de probabilidad clásica

Me gustaría que se imaginaran cuál sería la densidad de probabilidad para esta partícula moviéndose con energía total\(E\) y con\(V(x)\) variación como ilustran las tres gráficas anteriores. Para conceptualizar la densidad de probabilidad, imagina que la partícula tiene una lámpara parpadeante unida a ella y piensa en esta lámpara parpadeando digamos 100 veces por cada vez que tarda la partícula en completar un tránsito completo desde su punto de inflexión izquierdo, hasta su punto de inflexión derecho y de vuelta al primero. Los puntos de inflexión\(x_L\) y\(x_R\) son las posiciones en las que la partícula, si se moviera bajo las leyes de Newton, invertiría la dirección (a medida que el impulso cambia de signo) y da la vuelta. Estas posiciones se pueden encontrar preguntando a dónde va el impulso a cero:

\[0 = p = \sqrt{2m(E-V(x)}.\]

Estas son las posiciones donde toda la energía aparece como energía potencial\(E = V(x)\) y corresponden en las figuras anteriores a los puntos donde las líneas horizontales oscuras tocan las\(V(x)\) gráficas como se muestra en la gráfica central.

La densidad de probabilidad a cualquier valor de\(x\) representa la fracción de tiempo que la partícula pasa a este valor de\(x\) (es decir, dentro\(x\) y\(x+dx\)). Piense en formar esta densidad permitiendo que la lámpara parpadeante unida a la partícula arroje luz sobre una placa fotográfica que está expuesta a esta luz para muchas oscilaciones de la partícula entre\(x_L\) y\(x_R\). Alternativamente, se puede expresar la probabilidad de\(P(x) dx\) que la partícula\(x\) gaste entre y\(x + dx\) dividiendo la distancia espacial\(dx\) por la velocidad (p/m) de la partícula en el punto\(x\):

\[P(x)dx = \sqrt{2m(E-V(x))} \;m\; dx.\]

Debido a que\(E\) es constante a lo largo del movimiento de la partícula,\(P(x)\) será pequeño en\(x\) valores donde la partícula se mueve rápidamente (\(V\)es decir, donde es baja) y será alta donde la partícula se mueve lentamente (donde\(V\) es alta). Entonces, la placa fotográfica mostrará una región brillante donde\(V\) es alta (porque la partícula se mueve lentamente en tales regiones) y menos brillo donde\(V\) es bajo. Tenga en cuenta, sin embargo, que a medida que\(x\) se acerca a los puntos de inflexión clásicos, la velocidad se aproxima a cero, por\(P(x)\) lo que la expresión anterior para No significa que la probabilidad de encontrar la partícula en el punto de inflexión sea infinita; significa que ahí la densidad de probabilidad es infinita. Esta divergencia de\(P(x)\) es una característica de la densidad de probabilidad clásica que se verá muy diferente de la densidad de probabilidad cuántica.

La conclusión es que las densidades de probabilidad anticipadas al analizar la dinámica newtoniana clásica de esta partícula aparecerían como ilustran las gráficas de histograma que se muestran en la Figura 1.7.

Figura 1. 7 Gráficas de probabilidad clásicas para los tres potenciales mostrados

Donde la partícula tiene alta energía cinética (y por lo tanto menor\(V(x)\)), gasta menos tiempo y\(P(x)\) es pequeña. Donde la partícula se mueve lentamente, pasa más tiempo y\(P(x)\) es más grande. Para la gráfica de la derecha,\(V(x)\) es constante dentro de la “caja”, por lo que la velocidad es constante, de ahí\(P(x)\) es constante para todos los\(x\) valores dentro de esta caja unidimensional. Le pido que tenga en cuenta estas tramas porque son muy distintas de lo que se encuentra cuando se resuelve la ecuación de Schrödinger para este mismo problema. También por favor tenga en cuenta que estas parcelas representan lo que se espera si la partícula se moviera de acuerdo con la dinámica newtoniana clásica (¡que sabemos que no lo es!).

Tratamiento Quantum

Para resolver las funciones y energías de onda mecánica cuántica de este mismo tipo de problema, primero escribimos al operador hamiltoniano como se discutió anteriormente reemplazándolo\(p\) por\(-i\hbar \dfrac{d}{dx}\):

\[H = -\dfrac{ \hbar^2}{2m} \dfrac{d^2}{dx^2} + V(x).\]

Entonces tratamos de encontrar soluciones\(\psi(x)\) a\(H\psi = E\psi\) que obedezcan ciertas condiciones. Estas condiciones están relacionadas con el hecho de que\(|\psi (x)|^2\) se supone que es la densidad de probabilidad para encontrar la partícula entre\(x\) y\(x+dx\). Para que las cosas sean lo más simples posible, centrémonos en el potencial de caja que\(V\) se muestra en el lado derecho de la Figura 1. 7. Este potencial, expresado en función de\(x\) es:\(V(x) = \infty\) para\(x< 0\) y para\(x> L\);\(V(x) = 0\) para\(x\) entre\(0\) y\(L\).

El hecho de que\(V\) sea infinito para\(x< 0\) y para\(x> L\), y que la energía total\(E\) debe ser finita, dice que\(\psi\) debe desaparecer en estas dos regiones (\(y = 0\)para\(x< 0\) y para\(x> L\)). Esta condición significa que la partícula no puede acceder a regiones del espacio donde el potencial es infinito. La segunda condición que hacemos uso es que\(\psi (x)\) debe ser continua; esto significa que la probabilidad de que la partícula esté en\(x\) no puede relacionarse discontinuamente con la probabilidad de que esté en un punto cercano. También es cierto que la derivada espacial\(\dfrac{d\psi}{dx}\) debe ser continua excepto en puntos donde el potencial\(V(x)\) tiene una discontinuidad infinita como lo hace en el ejemplo mostrado a la derecha en la Figura 1.7. La continuidad de\(\dfrac{d\psi}{dx}\) se relaciona con la continuidad del impulso (recordar,\(-i \hbar \dfrac{\partial}{\partial x}\) es un operador de impulso). Cuando una partícula se mueve por debajo, por ejemplo, de uno de los dos potenciales mostrados a la izquierda o a la mitad de la Figura 1.7, el potencial cambia suavemente como intercambio de energía cinética y potencial durante el movimiento periódico. En contraste, cuando se mueve bajo el potencial a la derecha de la Figura 1.7, el potencial experimenta un cambio repentino de dirección cuando la partícula choca con cualquiera de las paredes. Entonces, incluso clásicamente, el impulso de la partícula sufre una discontinuidad en esos puntos de inflexión de pared dura. Estas condiciones de continuidad de\(\psi\) (y su primera derivada espacial) y que\(\psi\) deben desaparecer en regiones del espacio donde el potencial es extremadamente alto fueron postuladas por los pioneros de la mecánica cuántica para que las predicciones de la teoría cuántica estuvieran en línea con las experimentales observaciones.

Funciones Energías y Ondas

La ecuación diferencial de segundo orden

\[- \dfrac{\hbar^2}{2m} \dfrac{d^2\psi}{dx^2} + V(x)\psi = E\psi\]

tiene dos soluciones (porque es una ecuación de segundo orden) en la región entre\(x= 0\) y\(x= L\) donde\(V(x) = 0\):

\[\psi = \sin(kx)\]

y

\[\psi = \cos(kx),\]

donde\(k\) se define como

\[k=\sqrt{2mE/\hbar^2}.\]

De ahí que la solución más general sea alguna combinación de estos dos:

\[\psi = A \sin(kx) + B \cos(kx).\]

Podríamos, alternativamente usar\(\exp(ikx)\) y\(\exp(-ikx)\) como las dos soluciones independientes (lo hacemos más adelante en la Sección 1.4 para ilustrar) porque\(\sin(kx)\) y se\(\cos(kx)\) pueden reescribir en términos de\(\exp(ikx)\) y\(\exp(-ikx)\); es decir, abarcan exactamente el mismo espacio.

El hecho de que\(\psi\) debe desaparecer en\(x= 0\) (n.b., se\(\psi\) desvanece\(x< 0\) porque ahí\(V(x)\) es infinito y\(\psi\) es continuo, por lo que debe desaparecer en el punto\(x= 0\)) significa que la amplitud de ponderación del\(\cos(kx)\) término debe desaparecer porque\(\cos(kx) = 1\) al \(x = 0\). Es decir,

\[B = 0.\]

La amplitud del\(\sin(kx)\) término no se ve afectada por la condición que se\(\psi\) desvanece en\(x= 0\), ya que en\(\sin(kx)\) sí misma se desvanece en\(x= 0\). Entonces, ahora sabemos que\(\psi\) es realmente de la forma:

\[\psi(x) = A \sin(kx).\]

La condición que\(\psi\) también se desvanece en\(x= L\) (porque se desvanece para\(x < 0\) donde de\(V(x)\) nuevo es infinito) tiene dos posibles implicaciones. O bien\(A = 0\) o\(k\) debe ser tal que\(\sin(kL) = 0\). La opción\(A = 0\) conduciría a una respuesta\(\psi\) que se desvanece en todos los valores de\(x\) y por lo tanto una probabilidad que se desvanece en todas partes. Esto es inaceptable porque implicaría que la partícula nunca se observa en ningún lado.

La otra posibilidad es esa\(\sin(kL) = 0\). Exploremos esta respuesta porque ofrece el primer ejemplo de cuantificación de energía que probablemente hayas encontrado. Como sabéis, la función de pecado se desvanece en múltiplos integrales de\(p\). Por lo tanto,\(kL\) debe haber algún múltiplo de\(\pi\); llamemos al entero\(n\) y\(Lk = n\pi\) escribamos (usando la definición de\(k\)) en la forma:

\[L\sqrt{\dfrac{2mE}{\hbar^2}} = n\pi.\]

Resolviendo esta ecuación para la energía\(E\), obtenemos:

\[E = \dfrac{n^2 \pi^2 \hbar^2}{2mL^2}\]

Este resultado dice que los únicos valores de energía que son capaces de dar una función de onda\(\psi (x)\) que obedezca las condiciones anteriores son estos\(E\) valores específicos. Es decir, no todos los valores energéticos están permitidos en el sentido de que pueden producir\(\psi\) funciones que son continuas y desaparecen en regiones donde\(V(x)\) es infinito. Si uno usa una energía\(E\) que no es uno de los valores permitidos y la sustituye\(E\) en\(\sin(kx)\), la función resultante no desaparecerá en\(x = L\). Espero que la solución a este problema les recuerde la cuerda de violín que discutimos anteriormente. Recordemos que la cuerda de violín que se amarraba en\(x = 0\) y en\(x = L\) dio lugar a la cuantificación de la longitud de onda al igual que las condiciones\(\psi\) que son continuas en\(x = 0\) y\(x = L\) dieron cuantificación de energía.

Sustituir\(k = n\pi/L\) en\(\psi = A \sin(kx)\) da

\[\psi (x) = A \sin\Big(\dfrac{np_x}{L}\Big).\]

El valor de A se puede encontrar recordando que\(|\psi|^2\) se supone que representa la densidad de probabilidad para encontrar la partícula en\(x\). Se supone que tales densidades de probabilidad están normalizadas, lo que significa que su integral sobre todos los\(x\) valores debe equivaler a unidad. Entonces, podemos encontrar A requiriendo que

\[1 = \int |\psi(x)|^2 dx = |A|^2 \int \sin^2\Big(\dfrac{np_x}{L}\Big)​dx\]

donde la integral va desde\(x = 0\) hasta\(x = L\). Buscar la integral de\(\sin^2(ax)\) y resolver la ecuación anterior para la llamada constante de normalización\(A\) da

\(A = \sqrt{\dfrac{2}{L}}\)y así

\[\psi(x) = \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{np_x}{L}\Big).\]

Los valores que\(n\) pueden asumir son\(n = 1, 2, 3, \cdots\); la elección\(n = 0\) es inaceptable porque produciría una función de onda\(\psi(x)\) que se desvanece en absoluto\(x\).

Las funciones de onda dependientes de x y t completas se dan como

\[\Psi(x,t) = \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{np_x}{L}\Big) \exp\bigg[-\dfrac{it}{\hbar}\dfrac{n^2 \pi^2\hbar^2}{2mL^2}\bigg].\]

Observe que la densidad\(|\Psi(x,t)|^2\) de probabilidad espacial no depende del tiempo y es igual a\(|\psi(x)|^2\) porque el exponencial complejo desaparece cuando\(\Psi^*\Psi\) se forma. Esto significa que la probabilidad de encontrar la partícula a varios valores de\(x\) es independiente del tiempo.

Otra cosa que quiero que noten es que, a diferencia del caso de la dinámica clásica, no todos los valores energéticos\(E\) están permitidos. En la situación de la dinámica newtoniana,\(E\) podría especificarse y luego se determinó el impulso de la partícula a cualquier\(x\) valor dentro de un signo. En contraste, en la mecánica cuántica, se debe determinar, resolviendo la ecuación de Schrödinger, cuáles\(E\) son los valores permitidos de. Estos\(E\) valores son cuantificados, es decir, que ocurren solo para valores discretos\(E = \dfrac{n^2 \pi^2h^2}{2mL^2}\) determinados por un número cuántico\(n\), por la masa de la partícula m, y por características del potencial (\(L\)en este caso).

Densidades de Probabilidad

Veamos ahora algunas de las funciones de onda\(\psi (x)\) y comparemos las densidades de probabilidad\(|\psi (x)|^2\) que representan con las densidades de probabilidad clásicas discutidas anteriormente. Las funciones de\(n=2\) onda\(n=1\) y se muestran en la parte superior de la Figura 1.8. Las densidades de probabilidad cuántica correspondientes se muestran debajo de las funciones de onda en dos formatos (como\(x-y\) gráficas y gráficas sombreadas que podrían relacionarse con la forma de luz intermitente de monitorear la ubicación de la partícula que discutimos anteriormente).

Figura 1. 8. Las dos funciones de onda más bajas y densidades de probabilidad

En la Figura 1 se muestra un conjunto más completo de funciones de onda (para que\(n\) van de 1 a 7).

Figura 1. 9. Siete funciones y energías de onda más bajas

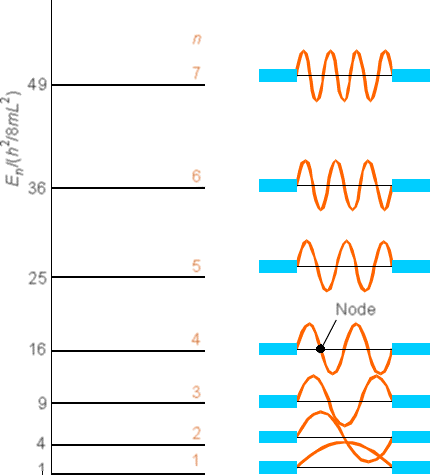
Observe que a medida que\(n\) aumenta el número cuántico, la energía\(E\) también aumenta (cuadráticamente con\(n\) en este caso) y el número de nodos en\(\psi\) también aumenta. También observe que las densidades de probabilidad son muy diferentes de lo que encontramos antes para el caso clásico. Por ejemplo, observe\(n = 2\) las densidades\(n = 1\) y y compárelas con la densidad clásica ilustrada en la Figura 1.10.

Figura 1.10. Densidad de probabilidad clásica para el potencial mostrado

La densidad clásica es fácil de entender porque estamos familiarizados con la dinámica clásica. En este caso, decimos que\(P(x)\) es constante dentro de la caja porque el hecho de que\(V(x)\) sea constante hace que la energía cinética y de ahí que la velocidad de la partícula se mantenga constante, y esto es cierto para cualquier energía\(E\). En contraste, la\(P(x)\) gráfica de la función de onda\(n = 1\) cuántica alcanza su punto máximo en el medio de la caja y cae a cero en las paredes. La\(n = 2\) densidad\(P(x)\) tiene dos picos (uno a la izquierda del punto medio de la caja y otro a la derecha), un nodo en el punto medio de la caja, y cae a cero en las paredes. Una cosa que a menudo me preguntan los estudiantes es “¿cómo pasa la partícula de estar en el pico izquierdo a estar en el pico derecho si tiene cero posibilidades de estar alguna vez en el punto medio donde está el nodo?” La dificultad con esta pregunta es que se plantea en una terminología que pide una respuesta dinámica clásica. Es decir, al preguntar “cómo se pone la partícula...” se está exigiendo una respuesta que implica describir su movimiento (es decir, se mueve de aquí en tiempo\(t_1\) a allá en tiempo\(t_2\)). Desafortunadamente, la mecánica cuántica no trata temas como la trayectoria de una partícula (es decir, dónde está en varios momentos) sino solo con su probabilidad de estar en algún lugar (es decir,\(|\psi|^2\)). En la siguiente sección se tratarán aún más cuestiones tan paradójicas.

Densidades de Probabilidad Clásica y Cuántica

Como se acaba de señalar, es tentador para la mayoría de los estudiantes principiantes de mecánica cuántica intentar interpretar el comportamiento cuántico de una partícula en términos clásicos. No obstante, esta aventura está llena de peligro y está destinada a fallar porque las pequeñas partículas de luz simplemente no se mueven de acuerdo con las leyes de Newton. Para ilustrar, intentemos entender qué tipo de movimiento (clásico) sería consistente con las\(P(x)\) gráficas\(n = 1\) o\(n = 2\) cuánticas mostradas en la Figura 1. 8. No obstante, como espero que ustedes anticipen, este intento de obtener una comprensión clásica de un resultado cuántico no funcionará en el sentido de que conducirá a resultados sin sentido. Mi punto al llevarte a intentar una comprensión tan clásica es enseñarte que los resultados clásicos y cuánticos son simplemente diferentes y que debes resistir el impulso de imponer una comprensión clásica sobre los resultados cuánticos al menos hasta que entiendas bajo qué circunstancias los resultados clásicos y cuánticos deben o no deben ser comparables.

Para el\(n = 1\) caso de la Figura 1.8, observamos que\(P(x)\) es más alto en el punto medio de la caja y desaparece en\(x = 0\) y\(x = L\). En un mundo de la mecánica clásica, esto significaría que la partícula se mueve lentamente cerca\(x = \dfrac{L}{2}\) y más rápidamente cerca\(x = 0\) y\(x = L\). Debido a que la energía total de la partícula\(E\) debe permanecer constante a medida que se mueve, en regiones donde se mueve lentamente, el potencial que experimenta debe ser alto, y donde se mueve rápidamente,\(V\) debe ser pequeño. Este análisis (n.b., basado en conceptos clásicos) nos llevaría a concluir que el\(n =1\)\(P(x)\) surge de que la partícula se mueve en un potencial que es alto cercano\(x = \dfrac{L}{2}\) y bajo a medida que se\(x\) acerca a 0 o L.

Un análisis similar de la\(P(x)\) parcela para nos\(n = 2\) llevaría a concluir que la partícula para la que esta es la correcta\(P(x)\) debe experimentar un potencial alto a medio camino entre\(x = 0\) y\(x = \dfrac{L}{2}\), alto a medio camino entre\(x = \dfrac{L}{2}\) y\(x = L\), y bajo cerca\(x = \dfrac{L}{2}\) y cerca \(x = 0\)y\(x = L\). Estas conclusiones son locas porque sabemos que el potencial\(V(x)\) para el que resolvimos la ecuación de Schrödinger para generar ambas funciones de onda (y ambas densidades de probabilidad) es constante entre\(x = 0\) y\(x = L\). Es decir, sabemos que lo mismo\(V(x)\) se aplica a la partícula que se mueve en los\(n = 2\) estados\(n = 1\) y, mientras que el análisis de movimiento clásico ofrecido anteriormente sugiere que\(V(x)\) es diferente para estos dos casos.

¿Qué tiene de malo nuestro intento de entender las\(P(x)\) tramas cuánticas? El error que cometimos fue al intentar aplicar las ecuaciones y conceptos de la dinámica clásica a una\(P(x)\) trama que no surgió del movimiento clásico. En pocas palabras, no se puede preguntar cómo se mueve la partícula (es decir, cuál es su velocidad en diversas posiciones) cuando la partícula está experimentando una dinámica cuántica. La mayoría de los estudiantes, cuando experimentan por primera vez funciones de onda cuántica y probabilidades cuánticas, intentan pensar en que la partícula se mueve de una manera clásica que es consistente con la cuántica\(P(x)\). Este intento de conservar un grado de comprensión clásica del movimiento de la partícula casi siempre se encuentra con frustración, como lo ilustré con el ejemplo anterior y lo ilustraré más adelante en otros casos.

Continuando con este primer ejemplo de cómo se resuelve la ecuación de Schrödinger y cómo se piensa de los\(E\) valores cuantificados y las funciones de onda\(\psi\), permítanme ofrecer una nota un poco más optimista que la ofrecida en la discusión anterior. Si examinamos la\(\psi(x)\) gráfica mostrada en la Figura 1.9 para\(n = 7\), and think of the corresponding \(P(x) = |\psi(x)|^2\), observamos que el\(P(x)\) plot would look something like that shown in Figure 1. 11.

Figura 1.11. Densidad de probabilidad cuántica para\(n = 7\) mostrar siete picos y seis nodos

Tendría siete máximos separados por seis nodos. Si tuviéramos que trazar\(|\psi(x)|^2\) para un\(n\) valor muy grande como\(n = 55\), encontraríamos una\(P(x)\) parcela con 55 máximos separados por 54 nodos, con los máximos separados aproximadamente por distancias de (1/55L). Tal trama, cuando se ve en un sentido de grano grueso (es decir, enfocándose con una visión algo borrosa en las posiciones y alturas de los máximos) se parece mucho a la\(P(x)\) trama clásica en la que\(P(x)\) es constante para todos\(x\). Otra forma de observar la diferencia entre las distribuciones de probabilidad cuántica bajo-n y alta-n se refleja en la llamada longitud de onda local de Broglie

\[\lambda_{\rm local}(x)=\dfrac{h}{\sqrt{2m(E-V(X))}}\]

Se puede demostrar que las probabilidades clásicas y cuánticas serán similares en regiones del espacio donde

\[\left|\dfrac{d\lambda_{\rm local}}{dx}\right| << 1.\]

Esta desigualdad será cierta cuando\(E\) sea mucho mayor que\(V\), lo que es consistente con la opinión de que los estados cuánticos altos se comportan clásicamente, pero no se mantendrá cuando esté solo ligeramente por encima\(V\) (\(E\)es decir, para estados cuánticos de baja energía y para cualquier estado cuántico cercano al clásico puntos de inflexión) o cuando\(E\) es menor que\(V\) (es decir, en regiones clásicamente prohibidas).

En resumen, es un resultado general de la mecánica cuántica que\(P(x)\) las distribuciones cuánticas para grandes números cuánticos toman la forma de lo clásico\(P(x)\) para el mismo potencial\(V\) que se utilizó para resolver la ecuación de Schrödinger excepto cerca de puntos de inflexión y en clásicamente prohibido regiones. También es cierto que, a cualquier energía especificada, los resultados clásicos y cuánticos concuerdan mejor cuando se trata de partículas pesadas que de partículas ligeras. Por ejemplo, una energía dada\(E\) corresponde a un número\(n\) cuántico mayor en la fórmula de partícula en caja\(E_n = \dfrac{n^2\hbar^2}{2mL^2}\) para una partícula más pesada que para una partícula más ligera. De ahí que las partículas más pesadas, que se mueven con una energía dada\(E\), tienen distribuciones de probabilidad más clásicas.

Para obtener perspectiva sobre este asunto, en la tabla que se muestra a continuación, doy los niveles de energía\(E_n = \dfrac{n^2\hbar^2}{2mL^2}\) en kcal mol ^-1 para una partícula cuya masa es de 1, 2000, 20,000 o 200,000 veces la masa de un electrón restringida a moverse dentro de una región unidimensional de longitud\(L\) (en unidades Bohr denotadas \(a_0\); 1\(a_0\) =0.529 Å).

Energías\(E_n\) (kcal mol ^-1) para varias\(m\) y\(L\) combinaciones

m = 1 m _e

	L = 1 a 0	L = 10 a 0	L = 100 a 0	L = 1000 a 0
m = 1 m e	3.1 x10 ^3 n ^2	3.1 x10 ^1 n ^2	3.1 x10 ^-1 n ^2	3.1 x10 ^-3 n ^2
m = 2000 m e	1.5 x10 ^0 n ^2	1.5 x10 ^-2 n ^2	1.5 x10 ^-4 n ^2	1.5 x10 ^-6 n ^2
m = 20,000 m e	1.5 x10 ^-1 n ^2	1.5 x10 ^-3 n ^2	1.5 x10 ^-5 n ^2	1.5 x10 ^-7 n ^2
m = 200,000 m e	1.5 x10 ^-2 n ^2	1.5 x10 ^-4 n ^2	1.5 x10 ^-6 n ^2	1.5 x10 ^-8 n ^2

Claramente, para los electrones, incluso cuando están libres para vagar por más de 50-500 nanómetros (e.g.,\(L = 100 a_0\) o\(L = 1000 a_0\)), no es necesario acceder a un estado cuántico muy alto para alcanzar 1 kcal mol ^-1 de energía (por ejemplo,\(n= 3\) sería adecuado para\(L =100 a_0\)). Recordemos, son estados cuánticos altos donde se espera que la distribución de probabilidad espacial clásica y cuántica sea similar. Entonces, al tratar electrones, uno probablemente (casi) siempre va a tener que hacer uso de la mecánica cuántica y uno no podrá confiar en la mecánica clásica.

Para núcleos ligeros, con masas cercanas a 2000 veces la masa del electrón, si la partícula está restringida a un pequeño rango de distancia (por ejemplo, 1-10\(a_0\)), nuevamente incluso los estados cuánticos bajos tendrán energías superiores a 1 kcal mol ^-1. Solo cuando es libre para moverse de 100 a 1000\(a_0\), 1 kcal mol ^-1 corresponde a números cuánticos relativamente grandes para los cuales se espera un comportamiento casi clásico. Los datos mostrados en la tabla anterior también se pueden utilizar para estimar cuándo se puede esperar un comportamiento cuántico como la condensación de Bose-Einstein. Cuando están restringidas a 100\(a_0\), las partículas en el rango de masa de 1 amu tienen energías de traslación en el rango\(0.15 n^2\) cal mol ^-1. Al darse cuenta de que\(RT = 1.98\) cal mol ^{-1 K -1}, esto significa que se necesitarían temperaturas de traslación cercanas a 0.1 K para hacer que estas partículas ocupen su estado\(n = 1\) fundamental.

Por el contrario, las partículas con masas en el rango de 100 amu, incluso cuando están restringidas

a distancias de ca. 5 Å, requieren\(n\) superar ca. 10 antes de tener 1 kcal mol ^-1 de energía traslacional. Cuando se limita a 50 Å, 1 kcal mol ^-1 requiere\(n\) superar 1000. Entonces, las partículas pesadas, incluso a bajas energías, se comportarán clásicamente excepto si están restringidas a distancias muy cortas.

Volveremos a encontrarnos con este llamado principal de correspondencia cuántico-clásica cuando examinemos otros problemas del modelo. Es una propiedad importante de las soluciones a la ecuación de Schrödinger porque es lo que nos permite cerrar la brecha entre usar la ecuación de Schrödinger para tratar partículas ligeras pequeñas y las ecuaciones de Newton para sistemas macroscópicos (grandes, pesados).

Propagación de tiempo de funciones de onda

Para una partícula en un sistema de caja que existe en un estado propio que\(\psi(x) = \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{np_x}{L}\Big)\) tiene una energía\(E_n = \dfrac{n^2 \pi^2\hbar^2}{2mL^2}\), la función de onda dependiente del tiempo es

\[\Psi(x,t) = \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{np_x}{L}\Big) \exp\Big(-\dfrac{itE_n}{\hbar}\Big),\]

que se puede generar aplicando el llamado operador de evolución temporal\(U(t,0)\) a la función de onda en\(t = 0\):

\[\Psi(x,t) = U(t,0) \Psi(x,0),\]

donde una forma explícita para\(U(t,t’)\) es:

\[U(t,t’) = \exp\bigg[-\dfrac{i(t-t’)H}{\hbar}\bigg].\]

La función\(\Psi(x,t)\) tiene una densidad de probabilidad espacial que no depende del tiempo porque

\[\Psi^*(x,t) \Psi(x,t) = \dfrac{2}{L} \sin^2\Big(\dfrac{np_x}{L}\Big) = \Psi^*(x,0) \Psi(x,0)\]

ya que\(\exp\Big(-\dfrac{itE_n}{\hbar}\Big) \exp\Big(\dfrac{itE_n}{\hbar}\Big) = 1\). Sin embargo, es posible preparar sistemas (incluso en entornos de laboratorio reales) en estados que no son estados propios únicos; a dichos estados los llamamos estados de superposición. Por ejemplo, considere una partícula que se mueve a lo largo del eje x dentro del potencial de caja pero en un estado cuya función de onda en algún momento inicial\(t = 0\) es

\[\Psi(x,0) = \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big) – \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big).\]

Se trata de una superposición de los\(n =1\) y\(n = 2\) los propios estados. La densidad de probabilidad asociada a esta función es

\[|\Psi(x,0)|^2 = \dfrac{1}{2}\Big\{\dfrac{2}{L} \sin^2\Big(\dfrac{1p_x}{L}\Big)+ \dfrac{2}{L} \sin^2\Big(\dfrac{2p_x}{L}\Big) -2\dfrac{2}{L} \sin\Big(\dfrac{1p_x}{L}\Big)\sin\Big(\dfrac{2p_x}{L}\Big)\Big\}.\]

\(n = 2\)Los componentes\(n = 1\) y, la superposición\(\Psi\) y la densidad de probabilidad a se\(t = 0\) muestran en los tres primeros paneles de la Figura 1.12.

Figura 1.12. Las funciones\(n = 1\) y\(n = 2\) onda (superior izquierda), su superposición (superior derecha), y las densidades de probabilidad\(t = 0\) (abajo izquierda) y evolucionadas en el tiempo (abajo a la derecha) de la superposición

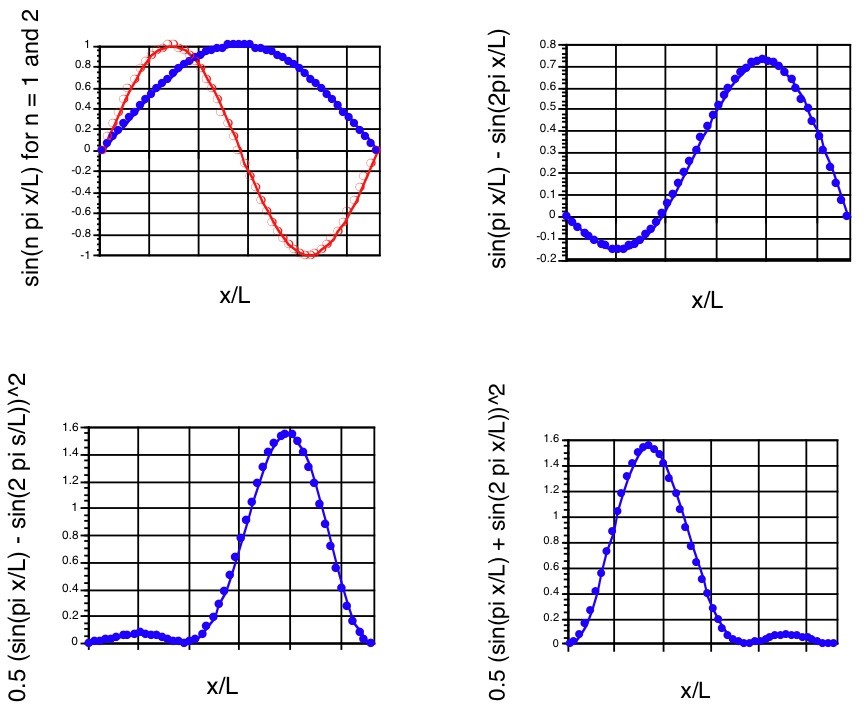
Cabe señalar que la densidad de probabilidad asociada a este estado de superposición no es simétrica alrededor del\(x=\dfrac{L}{2}\) punto medio aunque las funciones\(n = 1\) y densidades de onda y\(n = 2\) componente lo sean. Tal densidad describe la partícula localizada más fuertemente en la región grande-x de la caja que en la región pequeña-x en\(t = 0\).

Ahora, consideremos la función de onda de superposición y su densidad en momentos posteriores. Aplicando el operador de evolución temporal\(\exp\Big(-\dfrac{itH}{\hbar}\Big)\) para\(\Psi(x,0)\) generar esta función de evolución temporal en el tiempo t:

\[\Psi(x,t) = \exp\Big(-\dfrac{itH}{\hbar}\Big) \left\{\dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big) – \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big)\right\}\]

\[= {\dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big) \exp\Big(-\dfrac{itE_1}{\hbar}\Big) – \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big) \exp\Big(-\dfrac{itE_2}{\hbar}\Big) }.\]

La densidad de probabilidad espacial asociada a esto\(\Psi\) es:

\[|\Psi(x,t)|^2 = \dfrac{1}{2}\Bigg\{\dfrac{2}{L} \sin^2\Big(\dfrac{1p_x}{L}\Big)+ \dfrac{2}{L} \sin^2\Big(\dfrac{2p_x}{L}\Big)-2\dfrac{2}{L} \cos\Big(\dfrac{(E_2-E_1)t}{\hbar}\Big) \sin\Big(\dfrac{1p_x}{L}\Big)\sin\Big(\dfrac{2p_x}{L}\Big)\Bigg\}.\]

En\(t = 0\), esta función se reduce claramente a la escrita anteriormente para\(\Psi(x,0)\). Observe que a medida que el tiempo evoluciona, esta densidad cambia por el factor\(\cos(E_2-E_1)\tau/\hbar\)) que contiene. En particular, señalar que a medida que\(t\) se mueve a través de un periodo de tiempo\(\delta t = \dfrac{\pi\hbar}{E_2-E_1}\), el factor cos cambia de signo. Es decir, para\(t = 0\), el\(\cos\) factor es\(+1\); para\(t = \dfrac{\pi\hbar}{E_2-E_1}\), el factor cos es\(-1\); para\(t = \dfrac{2\pi\hbar}{E_2-E_1}\), vuelve a\(+1\). El resultado de esta variación temporal en el factor cos es que\(|\Psi|^2\) cambia de forma desde la que se muestra en el panel inferior izquierdo de la Figura 1. 12 a la mostrada en el panel inferior derecho (at\(t = \dfrac{\pi\hbar}{E_2-E_1}\)) y luego de vuelta a la forma en el panel inferior izquierdo (at\(t = \dfrac{2\pi\hbar}{E_2-E_1}\)). Se puede interpretar esta variación de tiempo como una descripción de la densidad de probabilidad de la partícula (¡no su posición clásica!) , inicialmente localizado hacia el lado derecho de la caja, moviéndose hacia la izquierda y luego de vuelta a la derecha. Por supuesto, esta evolución de tiempo continuará a lo largo de más y más ciclos a medida que el tiempo evolucione más.

Este ejemplo ilustra una vez más la dificultad de intentar localizar partículas que están siendo descritas por las funciones de onda cuántica. Por ejemplo, una partícula que se caracteriza por el estado propio\(\sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big)\) es más probable que se detecte cerca\(x = \dfrac{L}{2}\) que cerca\(x = 0\) o\(x = L\) porque el cuadrado de esta función es grande cerca\(x = \dfrac{L}{2}\). Una partícula en el estado\(\sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big)\) es más probable que se encuentre cerca\(x = \dfrac{L}{4}\) y\(x = \dfrac{3L}{4}\), pero no cerca\(x = 0\),\(x = \dfrac{L}{2}\), o\(x =L\). El tema de cómo la partícula en este último estado pasa de estar cerca\(x = \dfrac{L}{4}\) a no\(x = \dfrac{3L}{4}\) es algo de lo que trata la mecánica cuántica. La mecánica cuántica no nos permite seguir la trayectoria de la partícula que es lo que necesitamos saber cuando preguntamos cómo se mueve de un lugar a otro. Sin embargo, las funciones de onda de superposición pueden ofrecer, hasta cierto punto, la oportunidad de seguir el movimiento de la partícula.

Por ejemplo, el estado de superposición escrito anteriormente como

\(\dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big) – \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big)\)tiene una amplitud de probabilidad que cambia con el tiempo como se muestra en la Figura 1.12. Además, el pico mayor de esta amplitud se mueve de lado a lado dentro de la caja a medida que evoluciona el tiempo. Entonces, en este caso, podemos decir con qué frecuencia el pico mayor se mueve de un lado a otro. En cierto sentido, esto nos permite seguir los movimientos de la partícula, pero sólo en la medida en que estemos satisfechos con atribuir su ubicación a la posición del pico mayor en su distribución de probabilidad. Es decir, realmente no podemos seguir su ubicación precisa, pero podemos seguir la ubicación de donde es muy probable que se encuentre. Sin embargo, observe que el tiempo que tarda la partícula en moverse de derecha a izquierda\(t = \dfrac{\pi\hbar}{E_2-E_1}\) depende de la diferencia de energía entre los dos estados que contribuyen al estado de superposición, no a la energía de ninguno de estos estados, lo cual es muy diferente de lo que se esperaría si la partícula se estuviera moviendo clásicamente.

Estas son observaciones importantes que espero que el alumno tenga fresco en mente. También son ingredientes importantes en la dinámica cuántica moderna en la que los paquetes de ondas localizadas, que son similares a los autoestados superpuestos discutidos anteriormente, se utilizan para detallar la posición y velocidad del pico de densidad de probabilidad principal de una partícula.

El ejemplo anterior ilustra cómo un tiempo evoluciona una función de onda que se expresa como una combinación lineal (es decir, superposición) de estados propios del problema en cuestión. Existe una gran cantidad de esfuerzo actual en la comunidad de química teórica orientada a desarrollar aproximaciones eficientes al operador de la\(\exp\Big(-\dfrac{itH}{\hbar}\Big)\) evolución que no requieren\(\Psi(x,0)\) ser escritas explícitamente como una suma de autoestados. Esto es importante porque, para la mayoría de los sistemas de relevancia directa para las moléculas, no se puede resolver para los autoestados; simplemente es demasiado difícil hacerlo. Puede encontrar un tratamiento significativamente más detallado del tratamiento a nivel de investigación de esta materia en mi página de teoría y mi libro de texto QMIC. Sin embargo, dediquemos un poco de tiempo a una breve introducción a lo que implica.

El problema es expresar\(\exp\Big(-\dfrac{itH}{\hbar}\Big) \Psi(q_j)\), donde\(\Psi(q_j)\) está alguna función de onda inicial pero no un estado propio, de una manera que no requiera que uno encuentre primero los autoestados {\(\psi_J\)} de\(H\) y expandirse\(\Psi\) en términos de estos autoestados:

\[\Psi (t=0) = \sum_J C_J \psi_J\]

después de lo cual la función deseada se escribe como

\[\exp\Big(-\dfrac{itH}{\hbar}\Big) \Psi(q_j) = \sum_J C_J \psi_J \exp\Big(-\dfrac{itE_J}{\hbar}\Big).\]

La idea básica es romper al operador\(H\) en sus componentes cinéticos\(T\) y\(V\) energéticos potenciales y darse cuenta de que los operadores diferenciales aparecen\(T\) solo en. La importancia de esta observación radica en el hecho de que\(T\) y\(V\) no conmuten lo que significa que no\(TV\) es igual a\(VT\) (n.b., recordar que para dos cantidades conmutar significa que su orden de aparición no importa). ¿Por qué no se conmutan? Porque\(T\) contiene segundas derivadas con respecto a las coordenadas {q_j} de las que\(V\) depende, entonces, por ejemplo, no\(\dfrac{d^2}{dq^2}(V(q) \Psi(q))\) es igual a\(V(q)\dfrac{d^2}{dq^2}\Psi(q)\). El hecho de que\(T\) y\(V\) no se conmuten es importante porque el intento más obvio de aproximarse\(\exp\Big(-\dfrac{itH}{\hbar}\Big)\) es escribir este único exponencial en términos de\(\exp\Big(-\dfrac{itT}{\hbar}\Big)\) y\(\exp\Big(-\dfrac{itV}{\hbar}\Big)\). Sin embargo, la identidad

\[\exp\Big(-\dfrac{itH}{\hbar}\Big) = \exp\Big(-\dfrac{itV}{\hbar}\Big) \exp\Big(-\dfrac{itT}{\hbar}\Big)\]

no es plenamente válido como se puede ver expandiendo los tres factores exponenciales anteriores como\(\exp(x) = 1 + x + \dfrac{x^2}{2!} + \cdots,\) y señalando que los dos lados de la ecuación anterior sólo están de acuerdo si se puede asumir eso\(TV = VT\), lo cual, como señalamos, no es cierto.

En la mayoría de los enfoques modernos para la propagación del tiempo, uno divide el intervalo de tiempo\(t\) en muchos (es decir,\(P\) de ellos) pequeños segmentos de tiempo\(\tau = t/P\). Entonces se expresa el operador de evolución como un producto de propagadores de\(P\) corta duración (el estudiante ya debería estar familiarizado con el hecho de que\(H\)\(T\), y\(V\) son operadores, entonces, a partir de ahora ya no usaré necesariamente letras en negrita para estas cantidades):

\[\exp\Big(-\dfrac{itH}{\hbar}\Big) = \exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \cdots = \left[\exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \right]^P.\]

Si uno puede entonces desarrollar un medio eficiente de propagación por un corto tiempo\(\tau\), entonces uno puede hacerlo una y otra vez\(P\) veces para lograr la propagación deseada a tiempo completo.

Se puede demostrar que el operador exponencial que implica\(H\) puede aproximarse mejor en términos de los operadores\(T\) y\(V\) exponenciales de la siguiente manera:

\[\exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \approx \exp\Big(-\dfrac{\tau^2 (TV-VT)}{\hbar^2}\Big) \exp\Big(-\dfrac{i\tau V}{\hbar}\Big) \exp\Big(-\dfrac{i\tau T}{\hbar}\Big).\]

Entonces, si uno puede estar satisfecho con la propagación por intervalos de tiempo muy cortos (para que se pueda descuidar el\(\tau^2\) término), efectivamente se puede usar

\[\exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \approx \exp\Big(-\dfrac{i\tau V}{\hbar}\Big) \exp\Big(-\dfrac{i\tau T}{\hbar}\Big)\]

como aproximación para el propagador\(U(t,0)\). También se puede demostrar que la llamada expresión de corta duración dividida

\[\exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \approx \exp\Big(-\dfrac{i\tau ​V}{2\hbar}\Big) \exp\Big(-\dfrac{i\tau T}{\hbar}\Big) \exp\Big(-\dfrac{i\tau ​V}{2\hbar}\Big) \]

proporciona una representación aún más precisa del propagador a corto plazo (porque las expansiones de los lados izquierdo y derecho concuerdan con órdenes superiores en\(\tau/\hbar\)).

Para avanzar más, se expresa entonces\(\exp\Big(-\dfrac{i\tau T}{\hbar}\Big)\) actuar\(\exp\Big(-\dfrac{i\tau V}{2\hbar}\Big) \Psi(q)\) en términos de las funciones propias del operador de energía cinética\(T\). Tenga en cuenta que estas funciones propias no dependen de la naturaleza del potencial V, por lo que este paso es válido para todos y cada uno de los potenciales. Las funciones propias de\(T = - \dfrac{\hbar^2}{2m} \dfrac{d^2}{dq^2}\) son las funciones propias de impulso que discutimos anteriormente

\[\psi_p(q) =\dfrac{1}{\sqrt{2\pi}} \exp\Big(\dfrac{ipq}{\hbar}\Big)\]

y obedecen la siguiente ortogonalidad

\[\int \psi_p'*(q) \psi_p(q) dq = d(p'-p)\]

y relaciones de integridad

\[\int \psi_p(q) \psi_p^*(q') dp = d(q-q').\]

Escribiendo\(\exp\Big(-\dfrac{i\tau V}{2\hbar}\Big) \Psi(q)\) como

\[\exp\Big(-\dfrac{i\tau ​V}{2\hbar}\Big)\Psi(q) = \int dq’ \delta(q-q') \exp\Big(-\dfrac{i\tau ​V(q’)}{2\hbar}\Big)\Psi(q'),\]

y el uso de la expresión anterior para\(\delta(q-q')\) da:

\[\exp\Big(-\dfrac{i\tau ​V}{2\hbar}\Big)\Psi(q) = \int \int \psi_p(q) \psi_p^*(q') \exp\Big(-\dfrac{i\tau ​V(q’)}{2\hbar}\Big)\Psi(q') dq' dp.\]

Luego insertando las expresiones explícitas para\(\psi_p(q)\) y\(\psi_p^*(q')\) en términos de

\[\psi_p(q) =\dfrac{1}{\sqrt{2\pi}} \exp\Big(\dfrac{ipq}{\hbar}\Big)\]

da

\[\exp\Big(-\dfrac{i\tau V}{2\hbar}\Big)\Psi(q)\]

\[= \int \int\dfrac{1}{\sqrt{2\pi}} \exp\Big(\dfrac{ipq}{\hbar}\Big)\dfrac{1}{\sqrt{2\pi}} \exp\Big(-\dfrac{ipq'}{\hbar}\Big) \exp\Big(-\dfrac{i\tau V(q’)}{2\hbar}\Big)\Psi(q') dq' dp.\]

Ahora, permitiendo\(\exp\Big(-\dfrac{i\tau T}{\hbar}\Big)\) actuar sobre\(\exp\Big(-\dfrac{i\tau V}{2\hbar}\Big) \Psi(q)\) produce

\[\exp\Big(-\dfrac{i\tau T}{\hbar}\Big) \exp\Big(-\dfrac{i\tau V}{2\hbar}\Big)\Psi(q) =\]

\[ \int \int \exp\Big(-\dfrac{i\tau\pi^2\hbar^2}{2m\hbar}\Big)\dfrac{1}{\sqrt{2\pi}} \exp\Big(-\dfrac{ip(q-q')}{\hbar}\Big)\dfrac{1}{\sqrt{2\pi}} \exp\Big(-\dfrac{i\tau V(q’)}{2\hbar}\Big)\Psi(q') dq' dp.\]

La integral sobre\(p\) arriba se puede llevar a cabo analíticamente y da

\[\exp\Big(-\dfrac{i\tau T}{\hbar}\Big) \exp\Big(-\dfrac{i\tau V}{2\hbar}\Big)\Psi(q) =\]

\[\sqrt{\dfrac{m}{2i\pi \tau\hbar}} \int \exp\Big(\dfrac{im(q-q')^2}{2\tau\hbar}\Big) \exp\Big(-\dfrac{i\tau V(q’)}{2\hbar}\Big) \Psi(q') dq'.\]

Entonces, la expresión final para la función de onda propagada a corto plazo es:

\[\Psi(q.t) = \sqrt{\dfrac{m}{2i\pi \tau\hbar}}\exp\Big(-\dfrac{i\tau V(q)}{2\hbar}\Big)\int \exp\Big(\dfrac{im(q-q')^2}{2\tau\hbar}\Big) \exp\Big(-\dfrac{i\tau V(q’)}{2\hbar}\Big)\Psi(q') dq',\]

que es la ecuación de trabajo que se utiliza para calcular el\(\Psi(q,t)\) conocimiento\(\Psi(q)\). Observe que todo lo que uno necesita saber para aplicar esta fórmula es el potencial\(V(q)\) en cada punto del espacio. No es necesario conocer ninguna de las funciones propias del hamiltoniano para aplicar este método. Esto es especialmente atractivo cuando se trata de moléculas muy grandes o moléculas en medios condensados donde es esencialmente imposible determinar cualquiera de los autoestados y donde los espaciamientos de energía entre los propios estados son extremadamente pequeños. Sin embargo, uno tiene que usar esta fórmula una y otra vez para propagar la función de onda inicial a través de muchos pequeños pasos de tiempo\(\tau\) para lograr la propagación completa durante el intervalo de tiempo deseado\(t = P\tau\).

Debido a que este tipo de técnica de propagación del tiempo es un área de investigación muy activa en la comunidad teórica, es probable que continúe refinándose y mejorando. Una mayor discusión al respecto está más allá del alcance de este libro, por lo que no voy a ir más allá en esta dirección. El sitio web de la profesora Nancy Makri proporciona acceso a más información sobre el área de investigación de propagación cuántica del tiempo.

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

  Integrated by Tomoyuki Hayashi (UC Davis)