2.4: Hückel o Teoría de Vinculación Estrecha
- Page ID
- 70998
Ahora, examinemos qué determina el rango de energía en el que se dividen los\(p_\pi\) orbitales (por ejemplo, orbitales en polienos, metales, semiconductores\(\sigma\) o aisladores; u\(p_\sigma\) orbitales en un sólido;\(\sigma\) o orbitales\(\pi\) atómicos en una molécula). Sé que, en nuestra discusión anterior, hablamos del grado de superposición entre orbitales en átomos vecinos en relación con la división de energía, pero ahora es el momento de hacer este concepto más cuantitativo. Para comenzar, consideremos dos orbitales, uno sobre un átomo marcado con A y otro en un átomo vecino etiquetado como B; estos orbitales podrían ser, por ejemplo, los\(1s\) orbitales de dos átomos de hidrógeno, como ilustra la Figura 2.9.

Sin embargo, los dos orbitales podrían ser, en cambio, dos\(p_\pi\) orbitales en átomos de carbono vecinos, como se muestra en la Figura 2.10, ya que forman orbitales de\(\pi\)\(\pi^*\) unión y antiunión.

Figura 2.10. Dos\(p_\pi\) orbitales atómicos forman un orbital\(\pi^*\) molecular de unión\(\pi\) y antiunión.
En ambos casos, pensamos en formar los orbitales moleculares (MO)\(\phi_k\) como combinaciones lineales de los orbitales atómicos (AO) ca sobre los átomos constituyentes, y lo expresamos matemáticamente de la siguiente manera:
\[\phi_K = \sum_a C_{K,a} \chi_a,\]
donde\(C_{K,a}\) se denominan combinación lineal de orbitales atómicos para formar coeficientes orbitales moleculares (LCAO-MO). Se supone que los MO son soluciones a la ecuación de Schrödinger en la que el H hamiltoniano involucra la energía cinética del electrón así como los potenciales\(V_L\) y\(V_R\) detalla su atracción hacia los centros atómicos izquierdo y derecho (este hamiltoniano de un electrón es solo una aproximación para describiendo orbitales moleculares; tratamientos de electrones N más rigurosos se discutirán en el Capítulo 6):
\[H = - \dfrac{\hbar^2}{2m} \nabla^2 + V_L + V_R.\]
En contraste, los AO centrados en el átomo izquierdo A se supone que son soluciones de la ecuación de Schrödinger cuyo Hamiltoniano es\(H = - \dfrac{\hbar^2}{2m} \nabla^2 + V_L\), y los AO en el átomo derecho B tienen\(H = - \dfrac{\hbar^2}{2m} \nabla^2 + V_R\). Sustituir\(\phi_K = \sum_a C_{K,a} \chi_a\) en la ecuación de Schrödinger del MO
\[\textbf{H}\phi_K = \varepsilon_K \phi_K\]
y luego multiplicando a la izquierda por el complejo conjugado de\(\chi_b\) e integrándose sobre el\(r\),\(\theta\) y\(\phi\) coordenadas del electrón produce
\[\sum_a \langle \chi_b| - \dfrac{\hbar^2}{2m} \nabla^2 + V_L + V_R |\chi_a\rangle C_{K,a} = \varepsilon_K \sum_a \langle \chi_b|\chi_a\rangle C_{K,a}\]
Recordemos que la notación Dirac\(\langle a|b\rangle\) denota la integral de\(a^*\) y\(b\), y\(\langle a| op| b\rangle\) denota la integral de\(a^*\) y el operador op que actúa sobre b.
En lo que se conoce como el modelo de Hückel en química o el modelo de unión estrecha en la teoría de estado sólido, se aproximan las integrales entrando en el conjunto anterior de ecuaciones lineales de la siguiente manera:
- Se supone\(\langle \chi_b| - \dfrac{\hbar^2}{2m} \nabla^2 + V_L + V_R |\chi_b\rangle \) que la integral diagonal que involucra al AO centrada en el átomo derecho y etiquetada\(\chi_b\) es equivalente a\(\langle \chi_b| - \dfrac{\hbar^2}{2m} \nabla^2 + V_R |\chi_b\rangle \), lo que significa que se descuida la atracción neta de este orbital hacia el centro atómico izquierdo. Además, esta integral se aproxima en términos de la energía de unión (denotada\(\alpha\), no confundir con la función de espín electrónico a) para un electrón que ocupa el\(\chi_b\) orbital:\(\langle \chi_b| - \dfrac{\hbar^2}{2m} \nabla^2 + V_R |\chi_b\rangle = \alpha_b \). El significado físico de\(\alpha_b\) es la energía cinética del electrón en\(\chi_b\) más la atracción de este electrón hacia el centro atómico derecho mientras reside en\(\chi_b\). Por supuesto, se realiza una aproximación análoga para la integral diagonal que implica\(\chi_a\);\(\langle \chi_a| - \dfrac{\hbar^2}{2m} \nabla^2 + V_L |\chi_a\rangle = \alpha_a \). Estos\(\alpha\) valores son cantidades negativas porque, como es convención en la teoría de la estructura electrónica, las energías se miden en relación con la energía del electrón cuando se retira de la órbita y posee energía cinética cero.
- \(\langle \chi_b| - \dfrac{\hbar^2}{2m} \nabla^2 + V_L + V_R |\chi_a\rangle \)Las integrales fuera de la diagonal se expresan en términos de un parámetro\(\beta_{a,b}\) que se relaciona con la energía cinética y potencial del electrón mientras reside en la “región de superposición” en la que ambos\(\chi_a\) y no\(\chi_b\) se desvanecen. Esta región se muestra pictóricamente arriba como la región donde los orbitales izquierdo y derecho se tocan o se superponen. Se supone que la magnitud de\(\beta\) es proporcional al solapamiento\(S_{a,b}\) entre los dos AO:\(S_{a,b} = \langle \chi_a|\chi_b\rangle \). Resulta que\(\beta\) suele ser una cantidad negativa, que se puede ver escribiéndola como\(\langle \chi_b| - \dfrac{\hbar^2}{2m} \nabla^2 + V_R |\chi_a\rangle + \langle \chi_b| V_L |\chi_a\rangle \). Dado que\(\chi_a\) es una función propia de\(- \dfrac{\hbar^2}{2m} \nabla^2 + V_R\) tener el valor propio\(\alpha_a\), el primer término es igual a\(\alpha_a\) (una cantidad negativa) veces\(\langle \chi_b|\chi_a\rangle \), la superposición\(S\). La segunda cantidad\(\langle \chi_b| V_L |\chi_a\rangle \) es igual a la integral de la densidad de superposición\(\chi_b(r)\chi_a(r)\) multiplicada por el potencial (negativo) de Coulomb para una interacción atractiva del electrón con el centro atómico izquierdo. Entonces, siempre que\(\chi_b(r)\) y\(\chi_a(r)\) tengan solapamiento positivo, b resultará negativo.
iii. Finalmente, en el modelo Hückel más elemental o de unión estrecha, las integrales de superposición fuera de la diagonal\(\langle \chi_a|\chi_b\rangle =S_{a,b}\) se descuidan y se establecen iguales a cero en el lado derecho de la ecuación de valores propios de la matriz. No obstante, en algunos modelos de Hückel, se trata explícitamente el solapamiento entre orbitales vecinos, por lo que, en algunas de las discusiones a continuación vamos a retener\(S_{a,b}\).
Con estas aproximaciones de Hückel, el conjunto de ecuaciones que determinan las energías orbitales\(\varepsilon_K\) y los correspondientes coeficientes LCAO-MO\(C_{K,a}\) se escriben para el caso biorbital en cuestión como en las primeras ecuaciones\(2\times2\) matriciales que se muestran a continuación
\ [
\ left [\ begin {array} {cc}
\ alpha &\ beta\
\ beta &\ alpha
\ end {array}
\ right]
\ left [\ begin {array} {c}
C_L\\
C_R
\ end {array}
\ right]
=\ varepsilon
\ left [\ begin {array} {cc}
1 & S\\
S & 1
\ end {array}
\ right]
\ left [\ begin {array} {c}
C_L\\
C_R
\ end {array}
\ right]
\]
que a veces se escribe un
\ [
\ left [\ begin {array} {cc}
\ alpha-\ varepsilon &\ beta-\ varepsilon S\\
\ beta-\ varepsilon S &\ alpha-\ varepsilon
\ end {array}
\ right]
\ left [\ begin {array} {c}
C_L\\
C_R
\ end {array}
\ right]
=
\ left [\ begin {array} {c}
0\\
0
\ end {array}
\ right]
\]
Estas ecuaciones se reducen con la suposición de superposición cero a
\ [
\ left [\ begin {array} {cc}
\ alpha &\ beta\
\ beta &\ alpha
\ end {array}
\ right]
\ left [\ begin {array} {c}
C_L\\
C_R
\ end {array}
\ right]
=\ varepsilon
\ left [\ begin {array} {cc}
1 & 0\\
0 & 1
\ end {array}
\ right]
\ left [\ begin {array} {c}
C_L\\
C_R
\ end {array}
\ right]
\]
Los parámetros a son idénticos si los dos AO ca y\(\chi_b\) son idénticos, como sería el caso de la unión entre los dos\(1s\) orbitales de dos átomos de H o dos\(p_\pi\) orbitales 2 de dos átomos de C o dos orbitales 3s de dos átomos de Na. Si los orbitales izquierdo y derecho no fueran idénticos (por ejemplo, para la unión en HeH+ o para la\(\pi\) unión en un grupo C-O), sus valores a serían diferentes y el problema de la matriz de Hückel se vería así:
\ [
\ left [\ begin {array} {cc}
\ alpha &\ beta\
\ beta &\ alpha'
\ end {array}
\ right]
\ left [\ begin {array} {c}
C_L\\
C_R
\ end {array}
\ right]
=\ varepsilon
\ left [\ begin {array} {cc}
1 & S\\
S & 1
\ end {array}
\ right]
\ left [\ begin {array} {c}
C_L\\
C_R
\ end {array}
\ right]
\]
Para encontrar las energías MO que resultan de combinar los AO, se deben encontrar los valores de e para los cuales son válidas las ecuaciones anteriores. Tomando la\(2\times2\) matriz que consiste en e veces la matriz de superposición hacia el lado izquierdo, el conjunto de ecuaciones anterior se reduce al tercer conjunto mostrado anteriormente. Se sabe a partir del álgebra matricial que tal conjunto de ecuaciones lineales homogéneas (es decir, que tienen ceros en los lados de la derecha) puede tener soluciones no triviales (es decir, valores de\(C\) eso no son simplemente cero) solo si el determinante de la matriz en el lado izquierdo desaparece. Al establecer este determinante igual a cero se obtiene una ecuación cuadrática en la que los valores e son las incógnitas:
\[(\alpha-\varepsilon)^2 – (\beta - \varepsilon S)^2 = 0.\]
Esta ecuación cuadrática se puede factorizar en un producto
\[(\alpha - \beta - \varepsilon +\varepsilon S) (\alpha + \beta - \varepsilon -\varepsilon S) = 0\]
que cuenta con dos soluciones
\[\varepsilon = \frac{\alpha + \beta}{1 + S}, \text{ and } \varepsilon = \frac{\alpha - \beta}{1 – S}.\]
Como se discutió anteriormente, resulta que los valores b suelen ser negativos, por lo que la energía más baja de dicha solución es la\(\varepsilon = (\alpha + \beta)/(1 + S)\) solución, que da la energía del MO de unión. Observe que las energías de los MOs adherentes y antiadherentes no se desplazan simétricamente del valor a dentro de esta versión del modelo de Hückel que conserva el solapamiento orbital. De hecho, el orbital de unión se encuentra menor que b por debajo de a, y el MO antiadhesión se encuentra más que b por encima de a debido a\(1-S\) los factores\(1+S\) y en los respectivos denominadores. Esta disminución y elevación asimétrica de los MO en relación con las energías de los AO constituyentes se observa comúnmente en los enlaces químicos; es decir, el orbital antienlace es más antiaglutinante que el enlace orbital de\(\sigma\) unión i. Esto es otra cosa importante a tener en cuenta porque sus efectos invaden la unión química y la espectroscopia.
Habiendo observado el efecto de la inclusión de los efectos de superposición AO en el modelo de Hückel, debo admitir que es mucho más común utilizar la versión simplificada del modelo de Hückel en la que se ignoran los factores S. Al hacerlo, se obtienen patrones de energías orbitales MO que no reflejan la división asimétrica en los orbitales de unión y antiadhesión señalados anteriormente. Sin embargo, este enfoque simplificado es más fácil de usar y ofrece ordenamientos de energía MO cualitativamente correctos. Entonces, procedamos con nuestra discusión del modelo Hückel en su versión simplificada.
Para obtener los coeficientes LCAO-MO correspondientes a los MO de unión y antiunión, se sustituyen los valores a correspondientes en las ecuaciones lineales
\ [
\ left [\ begin {array} {cc}
\ alpha-\ varepsilon &\ beta\
\ beta &\ alpha-\ varepsilon
\ end {array}
\ derecha]
\ left [\ begin {array} {c}
C_L\\
C_R
\ end {array}
\ derecha]
=
\ izquierda [\ begin {array} {c}
0\\
0
\ end {array}
\ right]
\]
y resuelve para los\(C_a\) coeficientes (en realidad, uno puede resolver para todos, menos uno\(C_a\), y luego usar la normalización del MO para determinar el Ca final). Por ejemplo, para el MO de unión, sustituimos\(\varepsilon = \alpha + \beta\) en la ecuación matricial anterior y obtenemos dos ecuaciones para\(C_L\) y\(C_R\):
\[- \beta C_L + \beta C_R = 0\]
\[\beta C_L - \beta C_R = 0.\]
Estas dos ecuaciones claramente no son independientes; cualquiera de las dos se puede resolver para una C en términos de la otra C para dar:
\[C_L = C_R,\]
lo que significa que el MO de unión es
\[\phi = C_L (\chi_L + \chi_R).\]
El desconocido final, C_L, se obtiene señalando que se supone que f es una función normalizada\(\langle \phi|\phi\rangle = 1\). Dentro de esta versión del modelo de Hückel, en la que se descuida la superposición S, la normalización de f lleva a la siguiente condición:
\[1 = \langle \phi|\phi\rangle = C_\textbf{L}^2 (\langle \chi_L|\chi_L\rangle + \langle \chi_R\chi_R\rangle ) = 2 C_\textbf{L}^2\]
con el resultado final dependiendo de asumir que cada c también está normalizado. Entonces, finalmente, lo sabemos\(C_L = \frac{1}{\sqrt{2}}\), y de ahí el MO de vinculación es:
\[\phi = \frac{1}{\sqrt{2}} (\chi_L + \chi_R).\]
En realidad, la solución de también\(1 = 2 C_\textbf{L}^2\) podría haber cedido\(C_L = - \frac{1}{\sqrt{2}}\) y luego, habríamos
\[\phi = - \frac{1}{\sqrt{2}} (\chi_L + \chi_R).\]
Estas dos soluciones no son independientes (una es solo —1 veces la otra), por lo que solo se debe incluir una en la lista de MOs. Sin embargo, cualquiera es igual de bueno como el otro porque, como se muestra muy temprano en este texto, todas las propiedades físicas que uno calcula a partir de una función de onda dependen no de,\(\psi\) sino de las mismas\(\psi^*\psi\). Entonces, dos funciones de onda que difieren entre sí por un factor de signo general como tenemos aquí tienen exactamente lo mismo\(\psi^*\psi\) y por lo tanto son equivalentes.
De la misma manera, podemos sustituir\(\varepsilon = \alpha - \beta\) en la ecuación matricial y resolver\(C_R\) los valores de\(C_L\) lata que sean apropiados para el MO antiadhesión. Hacerlo, nos da:
\[\phi^* = \frac{1}{\sqrt{2}} (\chi_L - \chi_R)\]
o, alternativamente,
\[\phi^* = \frac{1}{\sqrt{2}} (\chi_R - \chi_L).\]
Nuevamente, el hecho de que cualquiera de las expresiones for\(\phi\) sea aceptable muestra una propiedad de todas las soluciones a cualquier ecuación de Schrödinger; cualquier múltiplo de una solución también es una solución. En el ejemplo anterior, las dos respuestas para\(\phi\) difieren por un factor multiplicativo de (-1).
Intentemos otro ejemplo para practicar usando Hückel o teoría de unión estrecha. En particular, me gustaría que imaginaran dos posibles estructuras para un cúmulo de tres átomos de Na (es decir, pretender que alguien se acercara a ti y te preguntara qué geometría crees que asumiría tal cúmulo en su estado electrónico fundamental), una lineal y otra un triángulo equilátero. Además, supongamos que las distancias Na-Na en ambos grupos son iguales (es decir, que la persona que solicita su ayuda teórica está dispuesta a asumir que las variaciones en la longitud de los enlaces no son el factor crucial para determinar qué estructura es favorecida). En la Figura 2.11, mostré los dos cúmulos candidatos y sus orbitales 3s.

Numerando los orbitales 3s de valencia de tres átomos de Na\(\chi_1\)\(\chi_2\), y\(\chi_3\), a continuación, configuramos la matriz 3x3 Hückel apropiada para las dos estructuras candidatas:
\ [
\ left [\ begin {array} {ccc}
\ alpha &\ beta &0\\
\ beta &\ alpha &\ alpha &\ beta\\
0 &\ beta &\ alpha
\ end {array}
\ derecha]
\]
para la estructura lineal (n.b., los ceros surgen porque\(\chi_1\) y\(\chi_3\) no se superponen y por lo tanto no tienen elemento de matriz de\(\beta\) acoplamiento). Alternativamente, para la estructura triangular, encontramos
\ [
\ left [\ begin {array} {ccc}
\ alpha &\ beta &\ beta\\ beta\
\ beta &\ alpha &\ beta &\ beta
\\ beta &\ beta &\ alpha
\ end {array}
\ derecha]
\]
como la matriz de Hückel. Cada una de estas matrices de 3x3 tendrá tres valores propios que obtenemos restando e de sus diagonales y estableciendo los determinantes de las matrices resultantes en cero. Para el caso lineal, hacerlo genera
\[(\alpha-\varepsilon)^3 – 2 \beta^2 (\alpha-\varepsilon\alpha-\varepsilon) = 0,\]
y para el caso del triángulo produce
\[(\alpha-\varepsilon)^3 –3 \beta^2 (\alpha-\varepsilon) + 2 \alpha-\varepsilon = 0.\]
La primera ecuación cúbica tiene tres soluciones que dan energías al MO:
\[\varepsilon = \alpha + \sqrt{2} \beta, \varepsilon = \alpha, \text{ and } \varepsilon = \alpha - \sqrt{2} \beta,\]
para los MO de unión, no unión y antiadhesión, respectivamente. La segunda ecuación cúbica también tiene tres soluciones
\[\varepsilon = \alpha + 2\beta, \varepsilon = \alpha - \beta , \text{ and } \varepsilon = \alpha - \beta.\]
Entonces, para las estructuras lineales y triangulares, los patrones de energía MO son como se muestra en la Figura 2.12.
Para el\(Na_3\) cúmulo neutro sobre el que se le preguntó, tiene tres electrones de valencia para distribuir entre los orbitales más bajos disponibles. En el caso lineal, colocamos dos electrones en el orbital más bajo y uno en el segundo orbital. Hacerlo produce un estado de 3 electrones con una energía total de\(E= 2(\alpha+\sqrt{2} \beta) + \alpha= 3\alpha +2\sqrt{2}\beta\). Alternativamente, para las especies triangulares, colocamos dos electrones en el MO más bajo y uno en cualquiera de los MOs degenerados dando como resultado un estado de 3 electrones con energía total\(E = 3 \alpha + 3\beta\). Debido a que b es una cantidad negativa, la energía total de la estructura triangular es menor que la de la estructura lineal desde entonces\(3 > 2\sqrt{2}\).
El ejemplo anterior ilustra cómo podemos usar Hückel o teoría de unión estrecha para hacer predicciones cualitativas (por ejemplo, cuál de dos formas es probable que sea de menor energía).
Observe que todo lo que uno necesita saber para aplicar dicho modelo a cualquier conjunto de orbitales atómicos que se superponen para formar MO es
- las energías de AO individuales a (que se relacionan con la electronegatividad de los AO),
- el grado en que los AO se acogen (los parámetros b que se relacionan con AO se superponen),
- una estructura geométrica asumida cuya energía se quiere estimar.
Este ejemplo y el ejemplo anterior pertinente\(H_2\) o el\(\pi\) enlace en etileno también introducen la idea de simetría. Saber, por ejemplo\(H_2\), que etileno y lineal\(Na_3\) tienen un plano de simetría izquierda-derecha nos permite resolver el problema de Hückel en términos de orbitales atómicos adaptados a la simetría más que en términos de orbitales atómicos primitivos como hicimos antes. Por ejemplo, para lineal\(Na_3\), podríamos usar las siguientes funciones adaptadas a la simetría:
\[\chi_2 {\rm and} \frac{1}{\sqrt{2}} (\chi_1 + \chi_3)\]
ambos de los cuales están incluso bajo reflexión a través del plano de simetría y
\[ \frac{1}{\sqrt{2}} (\chi_1 - \chi_3)\]
lo cual es extraño bajo reflexión. La matriz 3x3 Hückel tendría entonces la forma
\ [
\ left [\ begin {array} {ccc}
\ alpha &\ sqrt {2}\ beta &0\\
\ sqrt {2}\ beta &\ alpha &0\\
0 & 0 &\ alpha
\ end {array}
\ derecha]
\]
Por ejemplo,\(H_{1,2}\) y\(H_{2,3}\) se evalúan de la siguiente manera
\[ H_{1,2} = \langle \frac{1}{\sqrt{2}} (\chi_1 + \chi_3)|H|\chi_2\rangle = 2\frac{1}{\sqrt{2}} \beta\]
\[H_{2,3} = \langle \frac{1}{\sqrt{2}} (\chi_1 + \chi_3)|H| \frac{1}{\sqrt{2}} (\chi_1 - \chi_3)\rangle = \frac{1}{2}( \alpha + \beta - \beta - \alpha)= 0.\]
Los tres valores propios de la matriz de Hückel anterior se ven fácilmente como\(\alpha\)\(\alpha+\sqrt{2}\beta\), y\(\alpha-\sqrt{2}\beta\), exactamente como encontramos anteriormente. Entonces, no es necesario pasar por el proceso de formación de funciones adaptadas a la simetría; la matriz primitiva de Hückel dará las respuestas correctas aunque no lo hagas. Sin embargo, el uso de simetría nos permite romper el problema completo (3x3 en este caso) de Hückel en problemas separados de Hückel para cada componente de simetría (una función impar y dos funciones pares en este caso, por lo que una 1x1 y una\(2\times2\) sub - matriz).
Mientras estamos discutiendo el tema de la simetría, permítanme explicar brevemente el concepto de simetría aproximada nuevamente utilizando el problema anterior de Hückel ya que se aplica al etileno como ejemplo ilustrativo.
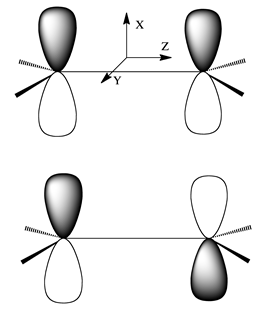
Claramente, como se ilustra en la Figura 2.12a, en su geometría de equilibrio la molécula de etileno tiene un plano de simetría (denotado\(\sigma_{X,Y}\)) que mapea núcleos y electrones de su izquierda a su derecha y viceversa. Este es el elemento de simetría que podría utilizarse para descomponer la matriz de\(2\times2\) Hückel describiendo\(\pi^*\) los orbitales\(\pi\) y en dos matrices 1x1. Sin embargo, si alguna de las cuatro longitudes de enlace C-H o ángulos de HCH se desplaza de su valor de equilibrio de manera que destruya la simetría perfecta de esta molécula, o si una de las unidades C-H fuera reemplazada por una unidad C-CH3, podría parecer que la simetría ya no sería una herramienta útil para analizar las propiedades de los orbitales moleculares de esta molécula. Afortunadamente, este no es el caso.
Incluso si no hay una simetría perfecta en el marco nuclear de esta molécula, los dos\(p_\pi\) orbitales atómicos se combinarán para producir un\(\pi^*\) orbital de unión\(\pi\) y antiunión. Además, estos dos orbitales moleculares seguirán poseyendo propiedades nodales similares a las mostradas en la Figura 2.12a a pesar de que no poseerán un carácter par e impar perfecto en relación con el\(\sigma_{X,Y}\) plano. El orbital de unión seguirá teniendo el mismo signo a la izquierda del\(\sigma_{X,Y}\) plano que a la derecha, y el orbital antiadhesión tendrá el signo opuesto a la izquierda que a la derecha, pero las magnitudes de estos dos orbitales no serán iguales de izquierda a derecha. Este es un ejemplo del concepto de simetría aproximada. Muestra que se puede utilizar la simetría, incluso cuando no es perfecta, para predecir los patrones nodales de los orbitales moleculares, y son los patrones nodales los que gobiernan las energías relativas de los orbitales como hemos visto una y otra vez.
Veamos si puedes hacer algo de esto por tu cuenta. Usando los resultados anteriores, ¿esperarías que el catión\(Na_3^+\) sea lineal o triangular? ¿Qué pasa con el anión\(Na_3^-\)? A continuación, quiero que sustituyan las energías MO de nuevo en la matriz 3x3 y encuentren los\(\chi_1\)\(\chi_2\),, y\(\chi_3\) coeficientes apropiados a cada uno de los 3 MO de la estructura lineal y triangular. Vea si hacerlo lo lleva a soluciones que se pueden representar como se muestra en la Figura 2.13, y vea si puede colocar cada conjunto de MO en el orden de energía adecuado.
Ahora, quiero mostrarles cómo ampliar sus horizontes y usar la teoría de unión estrecha para describir todos los enlaces en una molécula más complicada como el etileno que se muestra en la Figura 2.14. Lo que es diferente de este tipo de molécula cuando se compara con especies metálicas o conjugadas es que la unión puede describirse en términos de varios pares de orbitales de valencia que se acoplan para formar orbitales moleculares de enlace bicéntrico y antienlace. Dentro del modelo de Hückel descrito anteriormente, cada par de orbitales que se tocan o se superponen da lugar a una matriz 2x2. Más correctamente, todos los n orbitales de valencia constitutivos forman una matriz nxn, pero esta matriz se divide en bloques 2x2. Observe que esto no sucedió en el caso triangular Na3 donde cada AO tocó otros dos AO. Para el caso del etlieno, los orbitales de valencia consisten en (a) cuatro\(sp^2\) orbitales C equivalentes que se dirigen hacia los cuatro átomos H, (b) cuatro\(1s\) orbitales H, (c) dos\(sp^2\) orbitales C dirigidos uno hacia el otro para formar el\(\sigma\) enlace C-C, y (d) dos\(p_\pi\) orbitales C que formar el\(\pi\) enlace C-C. Este total de 12 orbitales genera 6 matrices de Hückel como se muestra debajo de la molécula de etileno.
Obtenemos una\(2\times2\) matriz para el\(\sigma\) enlace C-C de la forma
\ [
\ left [\ begin {array} {cc}
\ alpha_ {sp^2} &\ beta_ {sp^2, sp^2}\
\ beta_ {sp^2, sp^2} &\ alpha_ {sp^2}
\ end {array}
\ derecha]
\]
y una\(2\times2\) matriz para el\(\pi\) enlace C-C de la forma
\ [
\ left [\ begin {array} {cc}
\ alpha_ {p_\ pi} &\ beta_ {p_\ pi, p_\ pi}\\
\ beta_ {p_\ pi, p_\ pi} &\ alpha_ {p_\ pi}
\ end {array}
\ derecha]
\]
Finalmente, también se obtienen cuatro\(2\times2\) matrices idénticas para los enlaces C-H:
\ [
\ left [\ begin {array} {cc}
\ alpha_ {sp^2} &\ beta_ {sp^2, H}\\
\ beta_ {sp^2, H} &\ alpha_ {H}
\ end {array}
\ derecha]
\]
Las matrices anteriores producen
- cuatro MOS de unión C-H idénticos que tienen energías\[\varepsilon = \dfrac{(\alpha_H + \alpha_C) –\sqrt{(\alpha_H - \alpha_C)^2 + 2\beta^2}}{2},\]
- cuatro MOS antiunión C-H idénticos que tienen energías\[\varepsilon^* = \dfrac{(\alpha_H + \alpha_C) + \sqrt{(\alpha_H - \alpha_C)^2 + 2\beta^2}}{2},\]
- una unión C-C\(\pi\) orbital con\[\varepsilon = \alpha_{p\pi}+ \beta,\]
- un socio antiadhesión C-C orbital con\[\varepsilon^* = \alpha_{p\pi} - \beta,\]
- un MO de\(\sigma\) unión C-C con\[\varepsilon = \alpha_{sp^2}+ \beta,\] y (\ phi) su socio antiadhesión con\[\varepsilon^* = \alpha_{sp^2}- \beta.\]
En todas estas expresiones, se supone que el\(\beta\) parámetro es el apropiado para los orbitales específicos que se superponen como se muestra en las matrices.
Si deseas practicar este ejercicio de descomponer una molécula grande en conjuntos de valencia interactuante, trata de ver qué matrices de Hückel obtienes y qué energías MO de unión y antiunión obtienes para los orbitales de valencia de metano mostrados en la Figura 2.15.
Antes de dejar esta discusión sobre el modelo Hückel/Tight-binding, debo recalcar que tiene sus defectos (porque se basa en aproximaciones e implica descuidar ciertos términos en la ecuación de Schrödinger). Por ejemplo, predice (ver arriba) que el etileno tiene cuatro MOS de unión C-H energéticamente idénticos (y cuatro MOs antiligantes C-H degenerados). Sin embargo, esto no es lo que se ve cuando se utilizan espectros fotoelectrónicos para sondear las energías de estos MO. De igual manera, sugiere que el metano tiene cuatro orbitales equivalentes de unión C-H y antiadhesión, lo que, de nuevo, no es cierto. Resulta que, en cada uno de estos dos casos (etileno y metano), los experimentos indican una agrupación de cuatro MO de unión casi isoenergética y cuatro MO antiadherentes casi isoenergéticos. Sin embargo, existe cierta “división” entre estos grupos de cuatro MO. Las divisiones pueden interpretarse, dentro del modelo de Hückel, como derivadas de acoplamientos o interacciones entre, por ejemplo, un sp2 u\(sp^3\) orbital en un átomo de C dado y otro orbital similar en el mismo átomo. Tales acoplamientos hacen que la matriz nxn Hückel no bloquee la partición en grupos de\(2\times2\) submatrices porque ahora existen factores b fuera de la diagonal que acoplan un par de valencia dirigida a otro. Cuando tales acoplamientos se incluyen en el análisis, se encuentra que los grupos de MO que se espera que sean degenerados no están sino que se dividen tal como sugieren los datos de fotoelectrones.
Colaboradores y Atribuciones
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


