2.6: Túnel de electrones

Como ya hemos visto varias veces, las soluciones a la ecuación de Schrödinger muestran varias propiedades que son muy diferentes a las que se experimenta en la dinámica newtoniana. Una de las más inusuales e importantes es que las partículas que se describen utilizando la mecánica cuántica pueden moverse hacia regiones del espacio donde no se les permitiría ir si obedecieran ecuaciones clásicas. Llamamos a estas regiones clásicamente prohibidas. Consideremos un ejemplo para ilustrar este llamado fenómeno de tunelización. Específicamente, pensamos en un electrón (una partícula que probablemente usaríamos mecánica cuántica para describir) moviéndose en una dirección que llamaremos\(R\) bajo la influencia de un potencial que es:

1. Infinito para\(R < 0\) (esto podría, por ejemplo, representar una región del espacio dentro de un material sólido donde el electrón experimenta interacciones muy repulsivas con otros electrones);
2. Constante y negativo para algún rango de\(R\) entre\(R = 0\) y\(R_{\rm max}\) (esto podría representar la interacción atractiva de los electrones con esos átomos o moléculas en una región finita o superficie de un sólido);
3. Constante y repulsivo (es decir, positivo) por una cantidad\(\delta V + D_e\) para otra región finita de\(R_{\rm max}\) a\(R_{\rm max} +\delta\) (esto podría representar las interacciones repulsivas entre los electrones y una capa de moléculas de espesor d que se encuentran en la superficie del sólido en\(R_{\rm max}\));
4. Constante e igual\(R_{\rm max} +\delta\) a\(D_e\) desde el infinito (esto podría representar el electrón que se elimina del sólido, pero con una función de trabajo costo de energía de\(D_e\), y moviéndose libremente en el vacío por encima de la superficie y la capa de anuncios). Tal potencial se muestra en la Figura 2.18.

Figura 2.18. Potencial unidimensional que muestra un pozo, una barrera y la región asintótica.

La naturaleza fragmentada de este potencial permite resolver analíticamente la ecuación unidimensional de Schrödinger. Para las energías que se encuentran en el rango\(D_e < E < D_e +\delta V\), existe una clase de soluciones especialmente interesante. Estos llamados estados de resonancia ocurren en energías que están determinadas por la condición de que la amplitud de la función de onda dentro de la barrera (es decir, for\(0 \le R \le R_{\rm max}\)) sea grande. Pasemos ahora nuestra atención a este régimen energético específico, que también sirve para introducir el fenómeno de la tunelización.

\[k=\sqrt{\dfrac{2m_e E}{\hbar^2}},k'=\sqrt{\dfrac{2m_e (E-D_e)}{\hbar^2}},\kappa'=\sqrt{\dfrac{2m_e (D_e+\delta V-E)}{\hbar^2}}\]

Las soluciones fragmentadas a la ecuación de Schrödinger apropiadas para el caso de resonancia se escriben fácilmente en términos de pecado y cos o funciones exponenciales, utilizando las siguientes tres definiciones:

La combinación de\(\sin(kR)\) y\(\cos(kR)\) que resuelve la ecuación de Schrödinger en la región interna y que se desvanecen en\(R=0\) (porque la función debe desaparecer dentro de la región donde\(V\) es infinita y porque debe ser continua, debe desaparecer en\(R=0\)) es:

\[\psi = A\sin(kR) \hspace{1cm} (\text{for }0 \le R \le R_{\rm max} ).\]

En medio\(R_{\rm max}\) y\(R_{\rm max} +\delta\), hay dos soluciones que obedecen a la ecuación de Schrödiger, por lo que la solución más general es una combinación de estas dos:

\[\psi = B^+ \exp(\kappa'R) + B^- \exp(-\kappa'R) \hspace{1cm} (\text{for }R_{\rm max} \le R \le R_{\rm max} +\delta).\]

Finalmente, en la región más allá\(R_{\rm max} +\delta\), podemos usar una combinación de cualquiera\(\sin(k’R)\) y\(\cos(k’R)\) o\(\exp(ik’R)\) y\(\exp(-ik’R)\) para expresar la solución. A diferencia de la región cercana\(R=0\), donde era más conveniente usar las funciones pecado y cos porque una de ellas podía ser “desechada” ya que no podía cumplir con la condición límite de desaparecer en\(R=0\), en esta gran\(R\) región, cualquiera de los dos conjuntos es aceptable. Elegimos utilizar el\(\exp(ik’R)\) y

\(exp(-ik’R)\)set porque cada una de estas funciones es una función propia del operador de momentum\(-ih\dfrac{∂}{∂R}\). Esto nos permite discutir amplitudes para electrones que se mueven con impulso positivo y con impulso negativo. Entonces, en esta región, la solución más general es

\[\psi = C \exp(ik'R) + D \exp(-ik'R) \hspace{1cm} (\text{for }R_{\rm max} +\delta \le R < \infty).\]

Hay cuatro amplitudes (\(A, B^+, B^-,\)y\(C\)) que se pueden expresar en términos de la amplitud especificada\(D\) del flujo entrante (por ejemplo, pretender que conocemos el flujo de electrones que nuestro aparato experimental dispara en la superficie). Cuatro ecuaciones que se pueden utilizar para lograr este objetivo dan como resultado cuando\(\psi\) y\(\dfrac{d\psi}{dR}\) se emparejan en\(R_{\rm max}\) y en\(R_{\rm max} + \delta\) (una de las propiedades esenciales de las soluciones a la ecuación de Schrödinger es que ellas y su primera derivada son continuas; estas propiedades se relacionan con y siendo un probabilidad y\(-ih\dfrac{∂}{∂R}\) siendo continuo el impulso). Estas cuatro ecuaciones son:

\[A\sin(kR_{\rm max}) = B^+ \exp(\kappa'R_{\rm max}) + B^- \exp(-\kappa'R_{\rm max}),\]

\[Ak\cos(kR_{\rm max}) = \kappa'​B^+ \exp(\kappa'​R_{\rm max}) - \kappa'​B^- \exp(-\kappa'R_{\rm max}),\]

\[B^+ \exp(\kappa'(R_{\rm max} + \delta)) + B^- \exp(-\kappa'(R_{\rm max} + \delta))\]

\[= C \exp(ik'(R_{\rm max} + \delta) + D \exp(-ik'(R_{\rm max} + \delta),\]

\[k'B^+ \exp(\kappa'(R_{\rm max} + \delta)) - k'B^- \exp(-\kappa'(R_{\rm max} + \delta))\]

\[= ik'C \exp(ik'(R_{\rm max} + \delta)) -ik' D \exp(-ik'(R_{\rm max} + \delta)).\]

Es especialmente instructivo considerar el valor de lo\(A/D\) que resulta de resolver este conjunto de cuatro ecuaciones en cuatro incógnitas porque el módulo de esta relación proporciona información sobre la cantidad relativa de amplitud que existe dentro de la barrera en la región atractiva del potencial en comparación con que existe en la región asintótica como flujo entrante.

El resultado de resolver para\(A/D\) es:

\[\dfrac{A}{D} = \frac{4 \kappa'\exp(-ik'(R_{\rm max}+\delta))}{\exp(\kappa'\delta)(ik'-\kappa')(\kappa'\sin(kR_{\rm max})+k\cos(kR_{\rm max}))/ik'+ \exp(-\kappa'\delta)(ik'+\kappa')(\kappa'\sin(kR_{\rm max})-k\cos(kR_{\rm max}))/ik' }.\]

Para simplificar este resultado de una manera que se centre en condiciones donde la tunelización juega un papel clave en la creación de los estados de resonancia, es instructivo considerar este resultado en condiciones de barrera alta (grande\(D_e + \delta V - E\)) y gruesa (grande\(\delta\)). En tal caso, el factor\(\exp(-\kappa'\delta)\) será muy pequeño en comparación con su contraparte\(\exp(\kappa'\delta)\), y así

\[\dfrac{A}{D} = 4\frac{ik'\kappa'}{ik'-\kappa'} \frac{\exp(-ik'(R_{\rm max}+\delta)) \exp(-\kappa'\delta)}{\kappa'\sin(kR_{\rm max})+k\cos(kR_{\rm max}) }.\]

El\(\exp(-\kappa'\delta)\) factor in\(A/D\) hace que la magnitud de la función de onda dentro de la barrera sea pequeña en la mayoría de las circunstancias; decimos que el flujo incidente debe atravesar la barrera para llegar a la región interna y eso\(\exp(-\kappa'\delta)\) gobierna la probabilidad de este túnel.

Hay que tener en cuenta que, en el rango energético que estamos considerando (\(E < D_e+\delta\)), una partícula clásica ni siquiera pudo ingresar a la región\(R_{\rm max} < R < R_{\rm max} + \delta\); es por ello que llamamos a esto la región clásicamente prohibida o tuneladora. Una partícula clásica que comienza en la\(R\) región grande no puede entrar, y mucho menos penetrar, en esta región, por lo que tal partícula nunca podría terminar en la región\(0 <R < R_{\rm max}\) interna. Asimismo, una partícula clásica que comienza en la región interna nunca puede penetrar en la región de tunelización y escapar a la\(R\) región grande. Si no fuera por el hecho de que los electrones obedecen a una ecuación de Schrödinger más que a una dinámica newtoniana, no se produciría la tunelización y, por ejemplo, la microscopía de túnel de barrido (STM), que ha demostrado ser una herramienta maravillosa y poderosa para la obtención de imágenes de moléculas en y cerca de superficies, no existiría. De igual manera, muchos de los dispositivos que aparecen en nuestras modernas herramientas y juegos electrónicos, que dependen de las corrientes inducidas por la tunelización a través de diversas uniones, no estarían disponibles. Pero, o por supuesto, la tunelización sí ocurre y puede tener efectos notables.

Examinemos un fenómeno especialmente importante (en química) que se produce debido a la tunelización y que ocurre cuando la energía E asume valores muy especiales. La magnitud del\(A/D\) factor en las soluciones anteriores de la ecuación de Schrödinger puede llegar a ser grande si la energía E es tal que el denominador en la expresión anterior para se\(A/D\) aproxima a cero. Esto sucede cuando

\[\kappa'\sin(kR_{\rm max})+k\cos(kR_{\rm max})\]

o si

\[\tan(kR_{\rm max}) = - \frac{k}{\kappa}’.\]

Se puede demostrar que la condición anterior es similar a la condición de cuantificación de energía

\[\tan(kR_{\rm max}) = - \frac{k}{\kappa}\]

que surge cuando se unen estados de un potencial finito bien similar al mostrado arriba pero con la barrera entre\(R_{\rm max}\) y\(R_{\rm max} + \delta\) faltante y con\(E\) abajo\(D_e\). Hay, sin embargo, una diferencia. En la situación de estado límite, se producen dos parámetros relacionados con la energía

\[k =\sqrt{\dfrac{2\mu E}{\hbar^2}}\]

y

\[\kappa = \sqrt{\dfrac{2\mu (D_e-E)}{\hbar^2}} .\]

En el caso que ahora estamos considerando,\(k\) es lo mismo, pero

\[k' = \sqrt{\dfrac{2\mu (D_e+\delta V-E)}{\hbar^2}} \]

más que\(\kappa\) ocurre, por lo que las dos ecuaciones que implican no\(\tan(kR_{\rm max}) \) son idénticas, sino que son bastante similares.

Otra observación que es útil hacer sobre las situaciones en las que\(A/D\) se vuelve muy grande se puede hacer considerando el caso de una barrera muy alta (por lo que\(k'\) es mucho mayor que\(k\)). En este caso, el denominador que aparece en\(A/D\)

\[\kappa'\sin(kR_{\rm max})+k\cos(kR_{\rm max}) \simeq \kappa' \sin(kR_{\rm max})\]

puede llegar a ser pequeño en energías satisfactorias

\[\sin(kR_{\rm max}) \simeq 0.\]

Esta condición no es más que la condición de cuantificación de energía que ocurre para el potencial de partícula en una caja que se muestra en la Figura 2.19.

Figura 2.19. Potencial unidimensional similar al potencial de tunelización pero sin barrera ni región asintótica.

Este potencial es idéntico al potencial que estábamos examinando\(0 \le R \le R_{\rm max}\), pero se extiende hasta el infinito más allá\(R_{\rm max}\); la barrera y la asíntota de disociación mostrada por nuestro potencial están ausentes.

Consideremos qué nos enseñó este problema de tunelización\ hbaras. Primero, nos mostró que las partículas cuánticas penetran en regiones clásicamente prohibidas. Mostró que, a ciertas llamadas energías de resonancia, la tunelización es mucho más probable que en energías que están fuera de resonancia. En nuestro problema modelo, esto significa que los electrones que inciden en la superficie con energías cinéticas de resonancia tendrán una probabilidad muy alta de tunelización para producir un electrón que está altamente localizado (es decir, atrapado) en la\(0 < R < R_{\rm max}\) región. Asimismo, significa que un electrón preparado (por ejemplo, quizás por fotoexcitación desde un estado electrónico de menor energía) dentro de la\(0 < R < R_{\rm max}\) región permanecerá atrapado en esta región durante mucho tiempo (es decir, tendrá una baja probabilidad de tunelización hacia afuera).

En el caso que se acaba de mencionar, tendría sentido resolver las cuatro ecuaciones para la amplitud C de la onda saliente en la\(R > R_{\rm max}\) región en términos de la amplitud A. Si tuviéramos que resolver\(C/A\) y luego examinar en qué condiciones la amplitud de esta relación se volvería pequeña (así el electrón no puede escapar), encontraríamos la misma condición de\(\tan(kR_{\rm max}) = - \dfrac{k}{\kappa}'\) resonancia que encontramos desde el otro punto de vista. Esto significa que las energías de resonancia nos dicen para qué energías de colisión el electrón hará un túnel hacia adentro y producirá un electrón atrapado y, a estas mismas energías, un electrón que está atrapado no escapará rápidamente.

Siempre que uno tenga una barrera en una superficie de energía potencial, en energías por encima de la asíntota de disociación\(D_e\) pero por debajo de la parte superior de la barrera (\(D_e + \delta V\)aquí), uno puede esperar que los estados de resonancia ocurran en energías especiales de dispersión\(E\). Como ilustramos con el problema del modelo, estas llamadas energías de resonancia a menudo pueden ser aproximadas por las energías de estado límite de un potencial que es idéntico al potencial de interés en la región interna (\(0 \le R \le R_{\rm max}\)) pero que se extiende hasta el infinito más allá de la parte superior de la barrera (es decir, más allá de la barrera, no retrocede a los valores inferiores\(E\)).

La importancia química de las resonancias es grande. Las moléculas altamente excitadas rotacionalmente pueden tener energía total más que suficiente para disociarse (\(D_e\)), pero esta energía puede almacenarse en el movimiento de rotación, y la energía vibratoria puede ser menor que\(D_e\). En términos del modelo anterior, el alto momento angular rotacional puede producir una barrera centrífuga significativa en el potencial efectivo que caracteriza la vibración de la molécula, pero la energía vibratoria del sistema puede estar significativamente por debajo\(D_e\). En tal caso, y cuando se ve en términos de movimiento sobre un potencial efectivo modificado por un momento angular como el que muestro en la Figura 2.20, la vida útil de la molécula con respecto a la disociación está determinada por la velocidad de tunelización a través de la barrera.

Figura 2.20. Potencial radial para moléculas no rotativas (\(J = 0\)) y para moléculas rotativas.

En este caso, se habla de predisociación rotacional de la molécula. La vida útil t se puede estimar calculando la frecuencia n a la que el flujo que existe dentro\(R_{\rm max}\) golpea la barrera a\(R_{\rm max}\)

\[\nu = \frac{\hbar k}{2\mu R_{\rm max}} \hspace{2cm} ({\rm sec})^{-1}\]

y luego multiplicando por la probabilidad de\(P\) que el flujo atraviese la barrera de\(R_{\rm max}\) a\(R_{\rm max} + \delta\):

\[P = \exp(-2\kappa'\delta).\]

El resultado es que

\[\tau^{ -1}= \frac{\hbar k}{2\mu R_{\rm max}} \exp(-2\kappa'\delta)\]

con la energía\(E\) entrando\(k\) y\(\kappa'\) siendo determinada por la condición de resonancia: (\ kappa'\ sin (kR_ {\ rm max}) +k\ cos (kR_ {\ rm max})) = mínimo. Observamos que la probabilidad de tunelización\(\exp(-2\kappa'\delta)\) cae de manera exponencial con un factor dependiendo del ancho d de la barrera a través de la cual la partícula debe hacer un túnel multiplicada por\(\kappa'\), lo que depende de la altura de la barrera por\(D_e + \delta\) encima de la energía\(E\) disponible. Esta dependencia exponencial del grosor y la altura de las barreras es algo que debes tener en cuenta porque aparece en todas las expresiones de velocidad de tunelización.

Otro caso importante en el que se produce la tunelización es en estados electrónicamente metaestables de aniones. En los llamados estados de resonancia de forma, el electrón extra del anión experimenta un potencial atractivo debido a su interacción con el dipolo, cuadrupolo y momentos electrostáticos inducidos de la molécula neutra subyacente, así como un potencial centrífugo de la forma\(\dfrac{L(L+1)\hbar^2}{8\pi^2m_eR^2}\) cuya magnitud depende del ángulo carácter de la órbita que ocupa el electrón extra.

Al combinarse, los potenciales atractivos y centrífugos anteriores producen un potencial radial efectivo de la forma mostrada en la Figura 2.21 para el\(N_2^-\) caso en que el electrón agregado ocupe el\(\pi^*\) orbital que tiene\(L=2\) carácter cuando se ve desde el centro del enlace N-N. Nuevamente, el túnel a través de la barrera en este potencial determina la vida útil de tales estados de resonancia de forma.

Figura 2.21 Potencial radial efectivo para el exceso de electrones al\(N_2^-\) ocupar el\(\pi^*\) orbital que tiene un\(L = 2\) componente dominante.

Aunque los ejemplos tratados anteriormente involucraron analíticamente potenciales constantes por partes (por lo que la ecuación de Schrödinger y las condiciones de coincidencia de límites podrían resolverse exactamente), muchas de las características observadas se trasladan a situaciones químicamente más realistas. De hecho, a menudo se pueden modelar procesos de reacción química en términos de movimiento a lo largo de una (s) coordenada (s) de reacción a partir de una región característica de los materiales reactivos donde la superficie potencial está curvada positivamente en toda dirección y todas las fuerzas (es decir, gradientes del potencial a lo largo de todas las coordenadas internas) desaparecen; a un estado de transición en el que la curvatura de la superficie potencial a lo largo de s es negativa, mientras que todas las demás curvaturas son positivas y todas las fuerzas desaparecen; hacia los materiales del producto donde nuevamente todas las curvaturas son positivas y todas las fuerzas desaparecen. Una traza prototípica de la variación de energía a lo largo de dicha coordenada de reacción se encuentra en la Figura 2.22.

Figura 2.22. Perfil de energía a lo largo de una trayectoria de reacción que muestra la barrera a través de la cual se puede producir

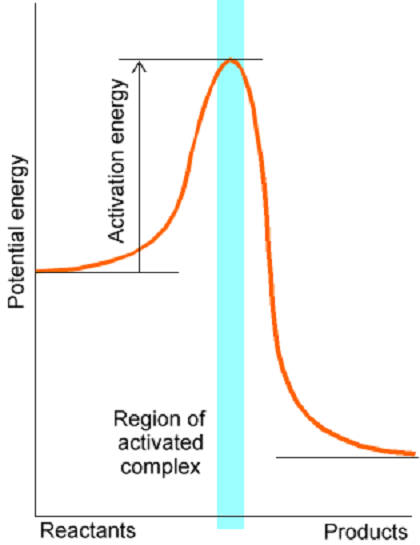
Cerca del estado de transición en la parte superior de la barrera en esta superficie, el túnel a través de la barrera juega un papel importante si las masas de las partículas que se mueven en esta región son suficientemente ligeras. Específicamente, si\(H\) o\(D\) átomos están involucrados en la ruptura del enlace y formación en esta región de la superficie de energía, generalmente se debe considerar la tunelización en el tratamiento de la dinámica.

Dentro del punto de vista de la trayectoria de reacción anterior, el movimiento transversal a la coordenada de reacción a menudo se modela en términos de movimiento armónico local aunque son posibles tratamientos más sofisticados de la dinámica. Esta imagen lleva a considerar el movimiento a lo largo de un solo grado de libertad, con respecto al cual gran parte del tratamiento anterior puede ser transportado, acoplado al movimiento transversal a lo largo de todos los demás grados internos de libertad que tienen lugar bajo un potencial completamente curvado positivamente (que por lo tanto produce restauración fuerzas a alejarse de la corriente trazada por la trayectoria de reacción). Este punto de vista constituye uno de los modelos más utilizados y exitosos de dinámica de reacción molecular y se trata con más detalle en los Capítulos 3 y 8 de este texto.

Colaboradores y Atribuciones

Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

Integrated by Tomoyuki Hayashi (UC Davis)