3.1: Estrategias para la optimización de la geometría y búsqueda de estados de transición
- Page ID
- 71100
La extensión de los modelos armónicos y vibracionales Morse a moléculas poliatómicas requiere que se analice la superficie de energía multidimensional de manera que permita aproximar los movimientos de la molécula en términos de muchas vibraciones casi independientes. En esta Sección, exploraremos las herramientas que se utilizan para llevar a cabo dicho análisis de la superficie, pero primero es importante describir cómo se localizan las geometrías de energía mínima y estado de transición en dichas superficies.
Encontrar Minima Local
Muchas estrategias que intentan ubicar mínimos en paisajes de energía potencial molecular comienzan por aproximar la energía potencial\(V\) para geometrías (denotada colectivamente en términos de coordenadas\(3N\) cartesianas\(\{q_j\}\)) en una expansión de la serie Taylor sobre alguna geometría de “punto de partida” (i.e. la geometría molecular actual en un proceso iterativo o una geometría que adivinaste como razonable para el estado mínimo o de transición que estás buscando):
\[V (g_k) = V(0) + \sum_k \left(\dfrac{\partial V}{\partial q_k}\right) q_k + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} q_k \, + \, ... \label{3.1.1}\]
Aquí,
- \(V(0)\)es la energía en la geometría actual,
- \(\dfrac{\partial{V}}{\partial{q_k}} = g_k\)es el gradiente de la energía a lo largo de la\(q_k\) coordenada,
- \(H_{j,k} = \dfrac{\partial^2{V}}{\partial{q_j}\partial{q_k}}\)es la segunda derivada o matriz de hessian, y
- \(g_k\)es la longitud del “paso” a dar a lo largo de esta dirección cartesiana.
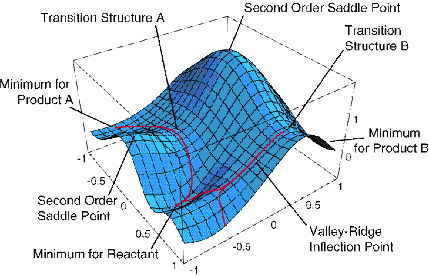
Un ejemplo de una superficie de energía en solo dos dimensiones se da en la Figura 3.1 donde se ilustran diversos aspectos especiales. Por ejemplo, se muestran mínimos correspondientes a estructuras moleculares estables, estados de transición (puntos de sillín de primer orden) que conectan dichos mínimos y puntos de sillín de orden superior.
Si el único conocimiento que está disponible es\(V(0)\) y los componentes del gradiente (por ejemplo, el cálculo de las segundas derivadas suele ser mucho más gravante computacionalmente que la evaluación del gradiente, por lo que a menudo se ve obligado a trabajar sin conocer los elementos de la matriz hessiana), la aproximación lineal
\[V(q_k) = V(0) + \sum_k g_K \,q_k \label{3.1.2}\]
sugiere que se deben elegir elementos de “paso”\(q_k\) que sean opuestos en signo al de los elementos de gradiente correspondientes\(g_k = \dfrac{\partial{V}}{\partial{q_k}}\) si se desea moverse “cuesta abajo” hacia un mínimo. La magnitud de los elementos escalonados generalmente se mantiene pequeña para permanecer dentro del “radio de confianza” dentro del cual la aproximación lineal a\(V\) es válida para alguna precisión deseada predeterminada (es decir, se quiere asegurar que no\(\sum_k g_K q_k\) es demasiado grande).
Cuando se dispone de datos de segunda derivada, existen diferentes enfoques para predecir qué paso {\(g_k\)} dar en busca de un mínimo, y es dentro de tales estrategias basadas en hessianas donde surge el concepto de pisar modos\(3N-6\) independientes. Primero escribimos la expansión cuadrática de Taylor
\[V (g_k) = V(0) + \sum_k g_K g_k + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} g_k\label{3.1.3}\]
en notación matriz-vector
\[V(\textbf{q}) = V(0) + \textbf{q}^{\textbf{T}} \cdot \textbf{g} + \dfrac{1}{2} \textbf{q}^{\textbf{T}} \cdot \textbf{H} \cdot \textbf{q} \label{3.1.4}\]
con los elementos\(\{g_k\}\) recogidos en el vector de columna\(\textbf{q}\) cuya transposición se denota\(\textbf{q}^{\textbf{T}}\).
Al introducir la matriz unitaria\(\textbf{U}\) que diagonaliza la\(\textbf{H}\) matriz simétrica, la ecuación anterior se convierte en
\[V(\textbf{q}) = V(0) + \textbf{q}^{\textbf{T}} \textbf{U} \, \textbf{U}^{\textbf{T}} \textbf{q} + \dfrac{1}{2} \textbf{q}^{\textbf{T}} \textbf{U} \, \textbf{U}^{\textbf{T}} \textbf{H} \textbf{U}\, \textbf{U}^{\textbf{T}} \textbf{q}. \label{3.1.5}\]
Porque\(\textbf{U}^{\textbf{T}}\textbf{H}\textbf{U}\) es diagonal, tenemos
\[(\textbf{U}^{\textbf{T}}\textbf{H}\textbf{U})_{k,l} = \delta_{k,l} \lambda_k \label{3.1.6}\]
donde\(\lambda_k\) están los valores propios de la matriz hessiana. Para las moléculas no lineales,\(3N-6\) de estos valores propios serán distintos de cero; para las moléculas lineales,\(3N-5\) serán distintos de cero. Los 5 o 6 valores propios cero de\(\textbf{H}\) tienen vectores propios que describen la traslación y rotación de toda la molécula; son cero porque la superficie de energía\(V\) no cambia si la molécula se gira o se traduce. Puede ser difícil identificar adecuadamente los 5 o 6 valores propios de traslación y rotación del hessiano porque los problemas de precisión numérica a menudo hacen que ocurran como valores propios muy pequeños positivos o negativos. Si la molécula que se estudia realmente posee valores propios internos (es decir, vibracionales) que son muy pequeños (por ejemplo, el movimiento torsional del grupo metilo en etano tiene una barrera de energía muy pequeña como resultado de lo cual la energía es muy débilmente dependiente de esta coordenada), hay que tener cuidado de identificar los valores propios de traslación y rotación internos. Al examinar los vectores propios correspondientes a todos los valores propios bajos de Hessian, se puede identificar y así separar el primero del segundo. En el resto de esta discusión, asumiré que las rotaciones y traslaciones se han identificado adecuadamente y las estrategias que discuto se referirán a utilizar los\(3N-6\) valores restantes\(3N-5\) o propios y vectores propios para llevar a cabo una serie de “pasos” de geometría diseñados para localizar mínimos de energía y estados de transición.
Los vectores propios de\(\textbf{H}\) forman las columnas de la matriz\(U\) que lleva\(H\) a la forma diagonal:
\[\sum_{\lambda} H_{k,l} U_{l,m} = \lambda_m U_{k,m} \label{3.1.7}\]
Por lo tanto, si definimos
\[Q_m = \sum_k U^T_{m,k} g_k \label{3.1.8a}\]
y
\[G_m = \sum_k U^T_{m,k} g_K \label{3.1.8b}\]
para ser el componente del paso\(\{g_k\}\) y del gradiente a lo largo del\(m^{th}\) vector propio de\(H\), la expansión cuadrática de se\(V\) puede escribir en términos de pasos a lo largo de las\(3N-6 \{Q_m\}\) direcciones\(3N-5\) o que corresponden a valores propios de hessian distintos de cero:
\[V (g_k) = V(0) + \sum_m G^T_m Q_m + \dfrac{1}{2} \sum_m Q_m \lambda_m Q_m.\label{3.1.9}\]
La ventaja de transformar el gradiente, paso, y hessian a la base de modo propio es que cada modo (etiquetado m) aparece en una forma independiente desacoplada en la expansión de\(V\). Esto nos permite dar pasos a lo largo de cada una de las\(Q_m\) direcciones de manera independiente con cada paso diseñado para disminuir la energía potencial cuando estamos buscando mínimos (las estrategias para encontrar un estado de transición se discutirán a continuación).
Para cada dirección de modo propio, se puede preguntar qué tamaño de paso\(Q\) sería la cantidad\(GQ + \dfrac{1}{2} \lambda Q^2\) mínima. Diferenciar esta forma cuadrática con respecto a\(Q\) y establecer el resultado igual a cero da
\[Q_m = - \dfrac{G_m}{\lambda_m} \label{3.1.10}\]
es decir, se debe dar un paso opuesto al gradiente pero con una magnitud dada por el gradiente dividido por el valor propio de la matriz hessiana. Si la geometría molecular actual es aquella que tiene todos los\(\lambda_m\) valores positivos, esto indica que uno puede estar “cerca” de un mínimo en la superficie de energía (porque todos\(\lambda_m\) son positivos en mínimos). En tal caso, el paso\(Q_m = - G_m/\lambda_m\) se opone al gradiente a lo largo de todas\(3N-5\) o\(3N-6\) direcciones, al igual que la estrategia basada en gradientes discutida anteriormente sugerida. El cambio de energía que se espera que ocurra si\(\{Q_m\}\) se da el paso se puede calcular sustituyendo\(Q_m = - G_m/\lambda_m\) en la ecuación cuadrática por\(V\):
\[V(\text{after step}) = V(0) + \sum_m G^T_m \bigg(- \dfrac{G_m}{\lambda_m}\bigg) + \dfrac{1}{2} \sum_m \lambda_m \bigg(- \dfrac{G_m}{\lambda_m}\bigg)^2 \label{3.1.11a}\]
\[= V(0) - \dfrac{1}{2} \sum_m \lambda_m \bigg(- \dfrac{G_m}{\lambda_m}\bigg)^2. \label{3.1.11b}\]
Esto sugiere claramente que el paso conducirá “cuesta abajo” en energía a lo largo de cada modo propio siempre que todos los\(\lambda_m\) valores sean positivos. Por ejemplo, si se comenzara con una buena estimación para las geometrías de equilibrio de etileno y propeno, se podría colocar estas dos moléculas a una distancia\(R_0\) mayor que la distancia de equilibrio entre fragmentos esperada\(R_{\rm vdW}\) en el complejo de van der Waals formado cuando interactúan. Debido a que ambos fragmentos están cerca de sus propias geometrías de equilibrio y\(R_0\) a una distancia a la que las fuerzas atractivas de largo alcance actuarán para unirlos, podría emplearse una estrategia como la señalada anteriormente para ubicar el mínimo de van der Waals en su superficie de energía. Este mínimo se representa cualitativamente en la Figura 3.1a.
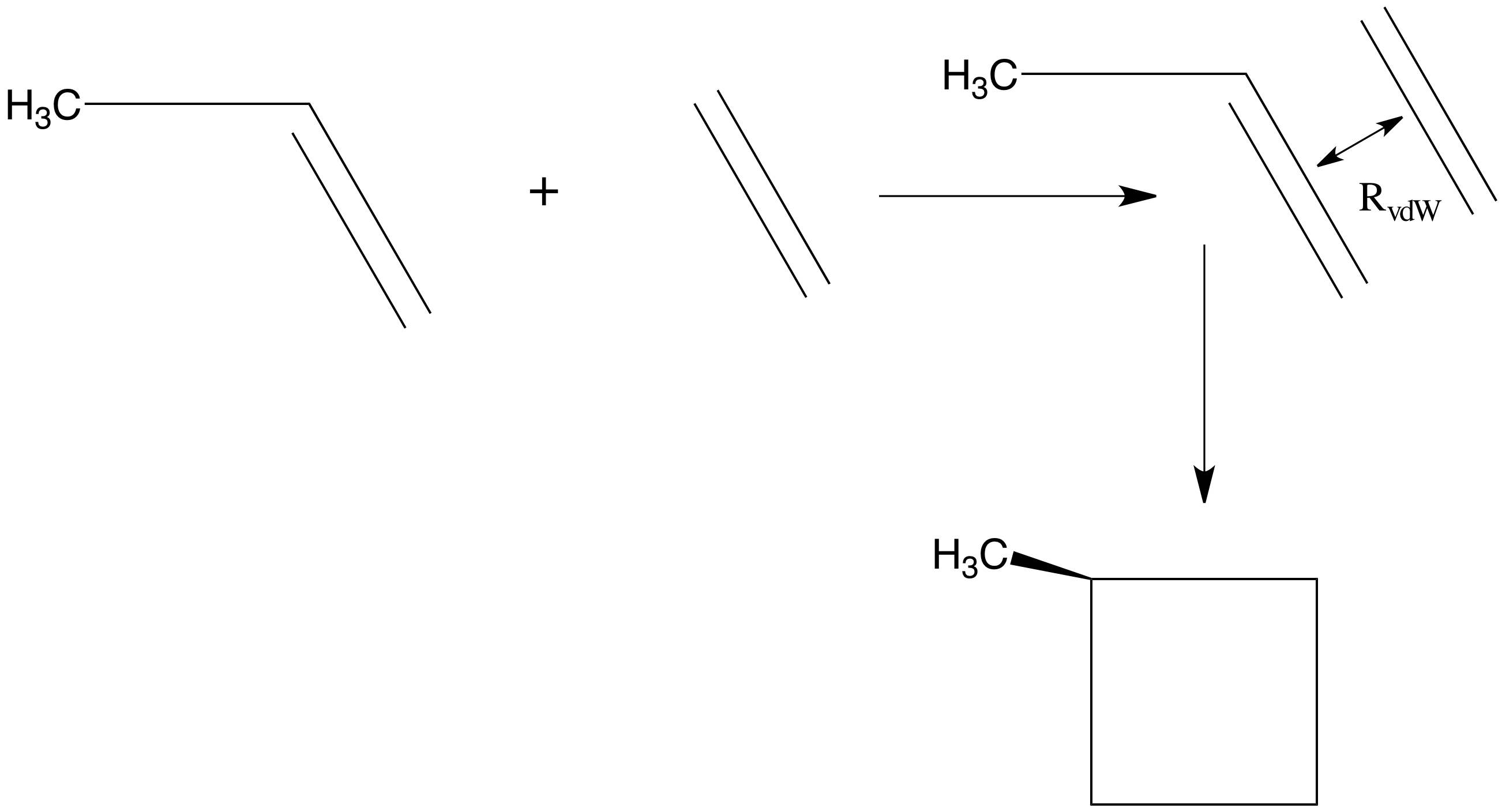
A partir de\(R_0\), uno encontraría que\(3N-6 = 39\) de los valores propios de la matriz de Hessian no son cero, donde\(N = 15\) está el número total de átomos en el complejo etileno-propeno. De estos 39 valores propios distintos de cero, tres tendrán vectores propios que describen desplazamientos radiales y angulares de los dos fragmentos uno respecto al otro; los 36 restantes describirán vibraciones internas del complejo. Los valores propios que pertenecen a los desplazamientos radiales y angulares entre fragmentos pueden ser positivos o negativos (porque no hizo ningún intento especial de orientar las moléculas en ángulos óptimos y puede que no haya adivinado muy bien en óptimo la distancia entre fragmentos de equilibrio), por lo que probablemente sería más prudente comenzar el proceso de minimización de energía usando información de gradiente para descender en energía hasta que se alcance una geometría\(R_1\) en la que los 39 valores propios de la matriz hessiana son positivos. A partir de ese momento, los pasos determinados tanto por el gradiente como por el hessian (i.e.,\(Q_m = - G_m/\lambda_m\)) se pueden usar a menos que uno encuentre una geometría en la que uno de los valores propios\(\lambda_m\) sea muy pequeño, en cuyo caso el paso\(Q_m = - G_m/\lambda_m\) a lo largo de este modo propio podría ser irrealistamente grande. En este caso, sería mejor no dar\(Q_m = - G_m/\lambda_m\) el paso en esta dirección en particular sino dar un pequeño paso en dirección opuesta a la pendiente para mejorar las posibilidades de moverse cuesta abajo. Tales problemas de valores propios pequeños podrían surgir, por ejemplo, si el ángulo de torsión del grupo metilo del propeno sucediera, durante la secuencia de pasos de geometría, para moverse hacia una región donde se accede a geometrías eclipsadas en lugar de escalonadas. Geometrías casi eclipsadas, el valor propio de Hessian que describe la torsión del grupo metilo es negativo; geometrías casi escalonadas, es positivo.
Siempre que uno o más de los\(\lambda_m\) sean negativos en la geometría actual, uno se encuentra en una región de la superficie de energía que no está lo suficientemente cerca de un mínimo para seguir ciegamente la prescripción a\(Q_m = - G_m/\lambda_m\) lo largo de todos los modos. Si solo uno\(\lambda_m\) es negativo, uno anticipa estar cerca de un estado de transición (en el que todos los componentes del gradiente desaparecen y todos menos uno\(\lambda_m\) son positivos con uno\(\lambda_m\) negativo). En tal caso, el análisis anterior sugiere dar un paso\(Q_m = - G_m/\lambda_m\) a lo largo de todos los modos teniendo positivo\(\lambda_m\), pero dando un paso de dirección opuesta (por ejemplo,\(Q_n = - G_n/\lambda_n\) a menos que\(\lambda_m\) sea muy pequeño en cuyo caso un pequeño paso opuesto\(G_n\) es mejor) a lo largo de la dirección que tiene negativo \(\lambda_n\)si uno está intentando avanzar hacia un mínimo. Esto es lo que recomendé en el párrafo anterior cuando se encuentra una geometría eclipsada (que es un estado de transición para la rotación del grupo metilo) si se busca un mínimo de energía.
Encontrar estados de transición
Por otro lado, si uno está en una región donde uno de los valores propios de hessian es negativo (y el resto son positivos) y si uno está buscando encontrar un estado de transición, entonces dar pasos a\(Q_m = - G_m/\lambda_m\) lo largo de todos los modos Tener valores propios positivos y tomar\(Q_n = - G_n/\lambda_n\) a lo largo del modo que tiene valor propio negativo es apropiado. Los escalones\(Q_m = - G_m/\lambda_m\) actuarán para mantener la energía cerca de su mínimo a lo largo de todas las direcciones menos una, y el escalón\(Q_n = - G_n/\lambda_n\) moverá el sistema cuesta arriba en energía a lo largo de la dirección que tiene curvatura negativa, exactamente como uno desea al “caminar” cuesta arriba en un cauce de río hacia un paso de montaña.
Sin embargo, incluso el procedimiento que se acaba de describir para encontrar un estado de transición puede producir resultados engañosos a menos que se use algún grado de intuición química. Permítanme dar un ejemplo para ilustrar este punto. Supongamos que se quiere encontrar comenzar cerca de la geometría del complejo de van der Waals que involucra etileno y propeno y luego ubicar el estado de transición en la ruta de reacción que conduce a los productos de cicloadición [2+2] metil-ciclobutano como también se muestra en la Figura 3.1a. Considera emplear cualquiera de dos estrategias para comenzar el “paseo” que va desde el complejo van der Waals al estado de transición deseado (TS):
- Uno podría encontrar el valor propio de hessian más bajo (sin traslación o no rotación) y dar un pequeño paso cuesta arriba a lo largo de esta dirección para comenzar una caminata de lecho de arroyo que podría conducir al TS. Usar el valor propio de hessian más pequeño para identificar una dirección a explorar tiene sentido porque es a lo largo de esta dirección que la superficie de energía se eleva de manera menos abrupta (al menos cerca de la geometría de los reactivos).
- Se podría mover el etileno radialmente un poco (digamos 0.2 Å) más cerca del propeno para generar una geometría inicial para comenzar la búsqueda TS. Esto tiene sentido porque se sabe que la reacción debe conducir a distancias entre fragmentos carbono-carbono que son mucho más cortas en los productos de metil-ciclobutano que en el complejo de van der Waals.
La primera estrategia sugerida anteriormente probablemente fracasará porque la serie de pasos generados al caminar cuesta arriba a lo largo del modo propio de Hesse más bajo producirá un camino que va desde la orientación eclipsada a la escalonada del grupo metilo del propeno. En efecto, este camino conduce a un TS, pero no es el TS de cicloadición [2+2] lo que queremos. La lección para llevar a casa aquí es que las caminatas cuesta arriba en el lecho de los arroyos comenzando como mínimo en la superficie de energía potencial de los reactivos pueden o no conducir al TS deseado. Tales caminatas no son tontas de intentar, pero uno debe examinar la naturaleza del modo propio que se sigue para juzgar si los desplazamientos a lo largo de este modo tienen sentido químico. Claramente, solo rotar el grupo metilo no es una buena manera de pasar de etileno y propeno a metil-ciclobutano.
La segunda estrategia sugerida anteriormente podría tener éxito, pero probablemente aún necesitaría ser refinada. Por ejemplo, si el desplazamiento del etileno hacia el propeno fuera demasiado pequeño, uno no habría distorsionado el sistema lo suficiente como para moverlo a una región donde la superficie de energía tiene una curvatura negativa a lo largo de la trayectoria de reacción como debe tener a medida que uno se acerca al TS. Entonces, si los modos propios hessianos cuyos vectores propios poseen desplazamientos radiales sustanciales entre fragmentos son todos positivos, probablemente uno no haya movido los dos fragmentos lo suficientemente cerca entre sí. Probablemente la mejor manera de proceder sería acercar los dos fragmentos aún más (o, moverlos a lo largo de una trayectoria sincrónica lineal [1] conectando los reactivos y los productos) hasta que se encuentre una geometría en la que el modo propio de un valor propio de Hesse negativo tenga componentes sustanciales a lo largo de lo que parece ser razonable para la ruta de reacción deseada (es decir, desplazamientos sustanciales que conducen a distancias más cortas entre fragmentos carbono-carbono). Una vez que uno ha encontrado tal geometría, uno puede usar las estrategias detalladas anteriormente (por ejemplo,\(Q_m = - G_m/\lambda_m\) para luego caminar cuesta arriba a lo largo de un modo mientras se minimiza a lo largo de los otros modos para moverse hacia el TS. Si tiene éxito, tal proceso conducirá al TS en el que todos los componentes del gradiente desaparecen y todos menos uno, el valor propio del hessiano es positivo. La lección para llevar a casa del ejemplo es que es prudente tratar de encontrar primero una geometría lo suficientemente cercana al TS para hacer que el hessian tenga un valor propio negativo cuyo vector propio tenga un carácter sustancial a lo largo de direcciones que tengan sentido químico para la ruta de reacción.
Ya sea en una serie de pasos hacia un mínimo o hacia un TS, una vez que se ha sugerido un paso dentro de la base del modo propio, se necesita expresar ese paso en términos de las coordenadas cartesianas originales\(q_k\) para que estos valores cartesianos puedan ser alterados dentro del programa de software para efectuar el paso predicho. Dados los valores para los componentes de\(3N-6\) paso\(3N-5\) o\(Q_m\) (n.b., los componentes de paso\(Q_m\) a lo largo de los 5 o 6 modos que tienen valores propios de hessian cero se pueden tomar como cero porque el simplemente traduciría o giraría la molécula), se debe calcular el {\(g_k\)}. Para ello, utilizamos la relación
\[Q_m = \sum_k U^T_{m,k} g_k\label{3.1.12}\]
y escribe su inversa (usando la naturaleza unitaria de la\(\textbf{U}\) matriz):
\[g_k = \sum_m U_{k,m} Q_m \label{3.1.13}\]
para calcular los componentes de paso cartesianos deseados.
Al usar los enfoques basados en hessianos descritos anteriormente, uno tiene que tener especial cuidado cuando uno o más de los valores propios de Hessian son pequeños. Esto sucede a menudo cuando
- uno tiene una molécula que contiene “modos blandos” (es decir, grados de libertad a lo largo de los cuales la energía varía poco), o
- a medida que uno se mueve de una región de curvatura negativa a una región de curvatura positiva (o viceversa); en tales casos, la curvatura debe moverse a través o cerca de cero.
Para estas situaciones, la expresión\(Q_m = - G_m/\lambda_m\) puede producir un paso muy grande a lo largo del modo que tiene una curvatura pequeña. Se debe tener cuidado para no permitir que se den pasos tan incorrectos artificialmente grandes.
Intersecciones de superficie de energía
Debo señalar que hay otras regiones importantes de superficies de energía potencial que uno debe ser capaz de localizar y caracterizar. Arriba, nos enfocamos en mínimos locales y estados de transición. Posteriormente en este Capítulo, y nuevamente en el Capítulo 8, discutiremos cómo seguir los llamados caminos de reacción que conectan estos dos tipos de puntos estacionarios utilizando el tipo de gradiente e información de hessian que introdujimos anteriormente en este Capítulo.
A veces es importante encontrar geometrías en las que dos superficies de energía Born-Oppenheimer\(V_1(\text{q})\) y se\(V_2(\text{q})\) cruzan porque tales regiones a menudo sirven como embudos eficientes para trayectorias o paquetes de ondas que evolucionan en una superficie para someterse a las llamadas transiciones no adiabáticas a la otra superficie. Pasemos unos minutos pensando en bajo qué circunstancias tales superficies pueden efectivamente cruzarse, porque los estudiantes a menudo escuchan que las superficies no se cruzan sino que, en cambio, se someten a cruces evitados. Para entender el tema, supongamos que tenemos dos funciones de onda\(\Phi_1\) y\(\Phi_2\) ambas dependen de\(3N-6\) coordenadas\(\{q\}\). Estas dos funciones no se suponen como funciones propias exactas del hamiltoniano\(H\), sino que probablemente se eligen para aproximar tales funciones propias. Para encontrar las funciones mejoradas\(\Psi_1\) y\(\Psi_2\) que representen con mayor precisión los autoestados, se suelen formar combinaciones lineales de\(\Phi_1\) y\(\Phi_2\),
\[ \Psi_K = C_{K,1} \Phi_1 + C_{K,2} \Phi_2 \label{3.1.14}\]
del que surge un problema de valor propio de matriz 2x2:
\ [\ izquierda|\ begin {array} {cc}
H_ {1,1} -E & H_ {1,2}\
H_ {2,1} & H_ {2,2} -E
\ end {array}\ derecha|=0\]
Esta ecuación cuadrática tiene dos soluciones
\[ 2E_\mp = (H_{1,1} + H_{2,2}) \pm \sqrt{(H_{1,1}+H_{2,2})^2 + 4H_{1,2}^2}\]
Estas dos soluciones pueden ser iguales (es decir, las dos energías de estado pueden cruzar) solo si el factor raíz cuadrada desaparece. Debido a que este factor es una suma de dos cuadrados (siendo cada uno por tanto cantidades positivas), esto solo puede suceder si dos identidades se mantienen simultáneamente (es decir, en la misma geometría):
\[H_{1,1} = H_{2,2} \label{3.1.15a}\]
y
\[H_{1,2} = 0. \label{3.1.15b}\]
El punto principal entonces es que en el espacio\(3N-6\) dimensional, los dos estados generalmente no tendrán la misma energía. Sin embargo, en un espacio de dos dimensiones inferiores (porque hay dos condiciones que deben obedecerse simultáneamente:\(H_{1,1} = H_{2,2}\) y\(H_{1,2} = 0\)), sus energías pueden ser iguales. No tienen que ser iguales, pero es posible que lo sean. Se basa en tal análisis que se suele decir que las superficies de energía potencial en\(3N-6\) dimensiones pueden sufrir intersecciones en espacios de dimensión\(3N-8\). Si los dos estados son de simetría diferente (por ejemplo, uno es un singlete y el otro un triplete), el elemento fuera de la diagonal se\(H_{1,2}\) desvanece automáticamente, por lo que solo se necesita otra condición para realizar el cruce. Entonces, decimos que dos estados de simetría diferente pueden cruzarse en un espacio de dimensión\(3N-7\). Para una molécula triatómica con grados\(3N-6 = 3\) internos de libertad, esto significa que superficies de la misma simetría pueden cruzarse en un espacio de dimensión 1 (es decir, a lo largo de una línea) mientras que las de diferente simetría pueden cruzarse en un espacio de dimensión 2 (es decir, en un plano). Un ejemplo de tal intersección de superficie se muestra en la Figura 3.1c.
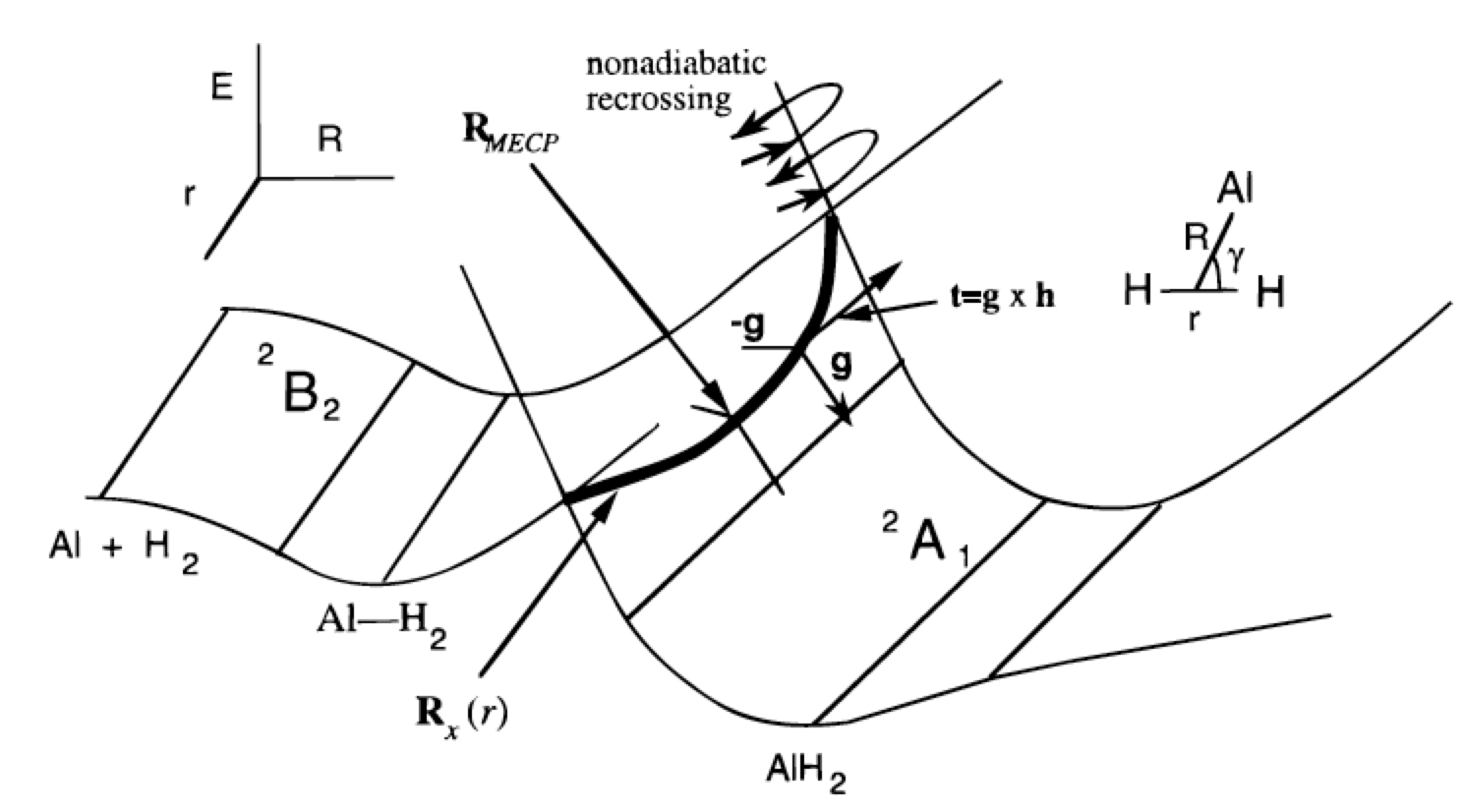
Primero considerando la reacción de Al (3s2 3p1; 2P) con\(H_2 (sg2; 1Sg+)\) para formar AlH2 (^^2A_1) como si ocurriera en\(C_{2v}\) simetría, el orbital 3p ocupado del\(Al\) átomo puede ser dirigido de cualquiera de tres maneras.
- Si se dirige hacia el punto medio del enlace H-H, produce un estado electrónico de\(^2A_1\) simetría.
- Si se dirige fuera del plano del\(AlH_2\), da un estado de\(2B_1\) simetría, y
- si se dirige paralelo al enlace H-H, genera un estado de\(^2B_2\) simetría.
El\(^2A_1\) estado es, como se muestra en la parte superior izquierda de la Figura 3.1c, repulsivo ya que los orbitales 3s y 3p del átomo de Al comienzan a superponerse con el\(\sigma_g\) orbital de la molécula de hidrógeno a grandes\(R\) valores. El\(^2B_2\) estado, en el que el orbital 3p ocupado se dirige lateralmente paralelo al enlace H-H, conduce a un pozo poco profundo de van der Waals a largo-R pero también se mueve a mayor energía a\(R\) valores más cortos.
El estado fundamental de la\(AlH_2\) molécula tiene sus cinco orbitales de valencia ocupados de la siguiente manera:
- dos electrones ocupan un enlace Al-H orbital de\(a_1\) simetría,
- dos electrones ocupan un enlace Al-H orbital de\(b_2\) simetría, y
- el electrón restante ocupa un orbital de\(sp^2\) carácter no enlazante localizado en el átomo de Al y que tiene simetría a1.
Esta ocupación\(a_1^2 b_2^2 a_1^1\) orbital del estado fundamental de la\(AlH_2\) molécula no se correlaciona directamente con ninguna de las tres configuraciones degeneradas del estado fundamental de las\(Al + H_2\) cuales son\(a_1^2 a_1^2 a_1^1, a_1^2 a_1^2 b_1^1\), y\(a_1^2 a_1^2 b_2^1\) como se explicó anteriormente. Es esta falta de correlación de configuración directa la que genera la barrera de reacción mostrada en la Figura 3.1c.
Volvamos ahora a la cuestión de encontrar el espacio de menor dimensión (\(3N-8\)o\(3N-7\)) en el que se cruzan dos superficies, asumiendo que se tiene información disponible sobre los gradientes y hessianos de ambas superficies energéticas\(V_1\) y\(V_2\). Hay dos componentes para caracterizar el espacio de intersección dentro de los cuales\(V_1\) =\(V_2\):
- Uno tiene que ubicar primero una geometría que se\(\textbf{q}_0\) encuentra dentro de este espacio y luego,
- uno tiene que muestrear geometrías cercanas (por ejemplo, que podrían tener menor energía total) que se encuentran dentro de este subespacio donde\(V_1 = V_2\).
Para ubicar una geometría en la que la función de diferencia\(F = [V_1 –V_2]^2\) pasa por cero, se pueden emplear métodos convencionales de minimización funcional, como los detallados anteriormente al discutir cómo encontrar mínimos de energía, para ubicar dónde\(F = 0\), pero ahora la función en la que se busca ubicar un mínimo en es la diferencia de la superficie de energía potencial.
Una vez localizada una de esas geometrías\(\textbf{q}_0\), posteriormente se intenta seguir la costura (es decir, para una molécula triatómica, esta es la línea unidimensional de cruce; para moléculas más grandes, es un espacio\(3N-8\) dimensional) dentro del cual la función\(F\) permanece cero. El profesor David Yaskony ha desarrollado rutinas eficientes para caracterizar dichos subespacios (D. R. Yaskony, Acc. Chem. Res. 31, 511-518 (1998)). La idea básica es parametrizar pasos lejos de (\(q_0\)) de una manera que restrinja tales pasos a no tener ningún componente a lo largo del gradiente de (\(H_{1,1} –H_{2,2}\)) o a lo largo del gradiente de\(H_{1,2}\). Porque\(V_1 = V_2\) requiere tener ambos\(H_{1,1} = H_{2,2}\) y\(H_{1,2} = 0\), dar pasos obedeciendo estas dos restricciones permite que uno permanezca dentro del subespacio donde\(H_{1,1} = H_{2,2}\) y\(H_{1,2} = 0\) sean obedecidos simultáneamente. Por supuesto, es una tarea formidable mapear todo el espacio\(3N-8\) o\(3N-7\) dimensional dentro del cual se cruzan las dos superficies, y esto esencialmente nunca se hace. En cambio, es común tratar de encontrar, por ejemplo, el punto dentro de este subespacio en el que las dos superficies tienen su menor energía. Un ejemplo de tal punto está etiquetado como RMECP en la Figura 3.1c, y sería de especial interés al estudiar las reacciones que tienen lugar en la superficie de menor energía que tienen que acceder a la costura de cruce de superficie para evolucionar sobre la superficie superior. La energía en RMECP refleja la energía más baja necesaria para acceder a este cruce de superficie.
Dichos procedimientos de ubicación de costura de intersección se emplean cada vez más comúnmente, pero aún están en desarrollo muy activo, por lo que remitiré al lector al artículo del profesor Yaskony citado anteriormente para obtener más orientación. Por ahora, debería bastar decir que ubicar tales intersecciones superficiales es un ingrediente importante cuando uno está interesado en estudiar, por ejemplo, reacciones fotoquímicas en las que los reactivos y productos pueden moverse de una superficie electrónica a otra, o reacciones térmicas que requieren que el sistema evolucione en un estado excitado a través de un cruce superficial.
Notas al final
- Se trata de una serie de geometrías\(R_x\) definidas a través de una interpolación lineal (usando un parámetro\(0 < x < 1\)) entre las coordenadas\(3N\) cartesianas\(R_{\rm reactants}\) pertenecientes a la geometría de equilibrio de los reactivos y las coordenadas correspondientes\(R_{\rm products}\) de los productos:\(R_x = R_{\rm reactants} x + (1-x) R_{\rm products}\)
Colaboradores y Atribuciones
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


