3.2: Modos normales de vibración

Habiendo visto cómo se puede usar información sobre los gradientes y hessianos en una superficie Born-Oppenheimer para ubicar geometrías correspondientes a especies estables y estados de transición, pasemos ahora para ver cómo se utilizan estos mismos datos para tratar las vibraciones en esta superficie.

Para una molécula poliatómica cuya dependencia de energía electrónica de las coordenadas\(3N\) cartesianas de sus\(N\) átomos, la energía potencial\(V\) puede expresarse (aproximadamente) en términos de una expansión de la serie Taylor sobre cualquiera de los mínimos locales. Por supuesto, diferentes mínimos locales (es decir, diferentes isómeros) tendrán diferentes valores para las coordenadas de equilibrio y para las derivadas de la energía con respecto a estas coordenadas. La expansión de la serie Taylor de la energía electrónica está escrita como:

\[V (g_k) = V(0) + \sum_k \left(\dfrac{\partial V}{\partial q_k}\right) q_k + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} q_k \, + \, ... \]

Aquí,

• \(V(0)\)es la energía en la geometría actual,
• \(\dfrac{\partial{V}}{\partial{q_k}} = g_k\)es el gradiente de la energía a lo largo de la\(q_k\) coordenada,
• \(H_{j,k} = \dfrac{\partial^2{V}}{\partial{q_j}\partial{q_k}}\)es la segunda derivada o matriz de hessian, y
• \(g_k\)es la longitud del “paso” a dar a lo largo de esta dirección cartesiana.

Si la geometría corresponde a un estado mínimo o de transición, los términos de gradiente desaparecerán todos, y la matriz hessiana poseerá\(3N - 5\) (para especies lineales) o\(3N -6\) (para moléculas no lineales) valores propios positivos y 5 o 6 valores propios cero (correspondientes a 3 traslacionales y 2 o 3 rotacionales movimientos de la molécula) para valores propios mínimos y uno negativos y/o valores propios\(3N-7\) positivos para un estado de transición.\(3N-6\)

Las ecuaciones de Newton del movimiento para la vibración

Las matrices de energía cinética y potencial

Truncando la serie Taylor en términos cuadráticos (asumiendo que estos términos dominan porque solo pequeños desplazamientos de la geometría de equilibrio son de interés), uno tiene el llamado potencial armónico:

\[V(q_k) = V(0) + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} q_k \label{3.2.1} \]

Las ecuaciones mecánicas clásicas de movimiento para las\(3N \{q_k\}\) coordenadas se pueden escribir en términos de la energía potencial anterior y la siguiente función de energía cinética:

\[T = \dfrac{1}{2} \sum_j m_j \left(\dfrac{dq_j}{dt}\right)^2, \label{3.2.2}\]

donde\(\dfrac{dq_j}{dt}\) es la tasa de cambio temporal de la coordenada\(q_j\) y\(m_j\) es la masa del átomo en el que reside la coordenada\(j^{th}\) cartesiana. Las ecuaciones de Newton así obtenidas son:

\[m_j\dfrac{d^2 q_j}{dt^2}=-\sum_k H_{j,k}q_k \]

donde la fuerza a lo largo de la\(j^{th}\) coordenada viene dada por menos la derivada del potencial\(V\) a lo largo de esta coordenada

\[\dfrac{\partial{V}}{\partial{q_j}}= \sum_k H_{j,k} q_k \label{3.2.3}\]

dentro de la aproximación armónica. Estas ecuaciones clásicas pueden expresarse de manera más compacta en términos de la evolución temporal de un conjunto de las llamadas coordenadas cartesianas ponderadas en masa definidas como:

\[x_j = q_j \sqrt{(m_j)} \label{3.2.4}\]

en términos de los cuales las ecuaciones de Newton anteriores se convierten

\[\dfrac{d^2 x_j}{dt^2}=-\sum_k H'_{j,k}x_k\]

y los elementos de la matriz de hessian ponderados en masa son

\[ H'_{j,k} = \dfrac{H_{j,k}}{ \sqrt{m_jm_k} }. \label{3.2.5}\]

Las energías vibracionales armónicas y los vectores propios de modo normal

Suponiendo que se\(x_j\) someten a alguna forma de evolución del tiempo sinusoidal:

\[x_j(t) = x_j (0) \cos(\omega t),\]

y sustituyendo esto en las ecuaciones de Newton produce una ecuación de valor propio de matriz:

\[\omega^2 x_j = \sum_k H'_{j,k} x_k \]

en el que los valores propios son los cuadrados de las llamadas frecuencias vibracionales de modo normal y los vectores propios dan las amplitudes de movimiento a lo largo de cada una de las coordenadas cartesianas\(3N\) ponderadas en masa que pertenecen a cada modo. Por lo tanto, para realizar un análisis en modo normal de una molécula, se forma la matriz de Hessian ponderada en masa y luego se encuentran los valores propios\(3N-5\) o\(3N-6\) distintos de cero, así\(\omega_j^2\) como los vectores propios correspondientes\(x_k^{(j)}\).

Es útil señalar que, si este mismo tipo de análisis se realizara en una geometría correspondiente a un estado de transición,\(3N-6\) o\(3N-7\) de los\(\omega_j^2\) valores sería positivo, pero uno de ellos sería negativo. El vector propio correspondiente al valor propio negativo de los puntos de Hessian ponderados en masa a lo largo de una dirección muy importante que discutiremos más adelante; es la dirección de la llamada coordenada de reacción intrínseca (IRC). Al informar los valores propios\(\omega_j^2\) en tal geometría de estado de transición, a menudo se dice que hay una frecuencia imaginaria porque uno de los\(\omega_j^2\) valores es negativo; este valor de\(\omega_j^2\) caracteriza la curvatura de la superficie de energía a lo largo del IRC en el estado de transición. Los valores propios vibracionales positivos de las geometrías de estado de transición se utilizan, como se discute en el Capítulo 8, para evaluar las funciones de partición de la mecánica estadística para las velocidades de reacción, y el\(\omega_j^2\) valor negativo juega un papel en la determinación del grado de tunelización a través de la barrera en la superficie de reacción.

Dentro de este tratamiento armónico del movimiento vibratorio, la energía vibratoria total de la molécula se da como

\[E(\nu_1, \nu_2, ··· \nu_{3N-5\text{ or }6}) =\sum_{j=1}^{3N-5\text{ or }6}\hbar\omega_j\Big(\nu_j+\dfrac{1}{2}\Big) \]

una suma\(3N-5\) o contribuciones\(3N-6\) independientes una para cada modo normal. La función de onda vibratoria total correspondiente

\[\Psi = \prod_{j=1}^{3N-5\text{ or }6} \psi\nu_j (x^{(j)}) \]

es un producto de\(3N-5\) o funciones de oscilador\(3N-6\) armónico\(\psi\nu_j (x^{(j)})\) uno para cada modo normal. La brecha de energía entre un nivel vibracional y otro en el que uno de los números\( \nu_j\) cuánticos se incrementa por unidad (es decir, para transiciones vibracionales fundamentales) es

\[\Delta E_{\nu_j} \rightarrow \nu_j + 1 = \hbar \omega_j \]

El modelo armónico predice así que las transiciones “fundamental” (\(\nu=0 \rightarrow \nu = 1\)) y “banda caliente” (\(\nu=1 \rightarrow \nu = 2\)) deben ocurrir con la misma energía, y las transiciones de armónicos (\(\nu=0 \rightarrow \nu=2\)) deben ocurrir exactamente al doble de esta energía.

Uno podría preguntarse si las coordenadas cartesianas ponderadas en masa serían mejores o más apropiadas para usar al ubicar mínimos y estados de transición en superficies energéticas Born-Oppenheimer. Si bien las coordenadas ponderadas en masa son de hecho esenciales para evaluar las frecuencias vibracionales armónicas y, como veremos más adelante, para trazar las llamadas rutas de reacción intrínsecas, su uso produce los mismos mínimos y estados de transición que se encuentran usando coordenadas ponderadas en masa. Esto se debe a que la condición de que todos los componentes del gradiente

\[\dfrac{\partial V}{\partial q_j}=0\]

de la superficie de energía desaparecer en un mínimo o en un estado de transición se obedecerá automáticamente cuando se expresa en términos de coordenadas ponderadas en masa ya que

\[\dfrac{\partial V}{\partial q_j}=\dfrac{\partial V}{\partial x_j}\dfrac{\partial x_j}{\partial q_j}=\dfrac{\partial V}{\partial x_j}\sqrt{m_j}\]

Observe que esto significa que las geometrías de todos los mínimos locales y estados de transición en una superficie dada de Born-Oppenheimer serán exactamente las mismas independientemente de qué isótopos aparezcan en la molécula. Por ejemplo, para las reacciones

\[ H-CN \rightarrow H-NC \]

o

\[D-CN \rightarrow D-NC \]

\[ H_2C=O \rightarrow H_2 + CO\]

o

\[HDC=O \rightarrow HD + CO\]

o

\[D_2C=O \rightarrow D_2 + CO \]

las geometrías de los reactivos, productos y estados de transición (para cada una de las distintas reacciones) no dependerán de la identidad de los isótopos de hidrógeno. Sin embargo, las frecuencias vibracionales armónicas dependerán de los isótopos porque el Hessian ponderado en masa difiere del hessiano expresado en términos de coordenadas no ponderadas en masa.

El uso de la simetría

Modos adaptados a simetría

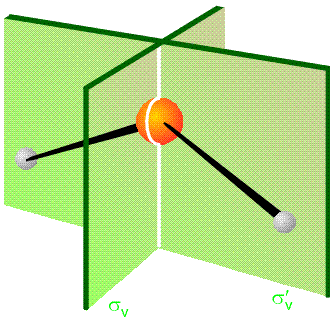
A menudo es posible simplificar el cálculo de las frecuencias armónicas de modo normal y los vectores propios mediante la explotación de la simetría del grupo de puntos moleculares. Para las moléculas que poseen simetría en una geometría estable particular, el potencial electrónico\(V(q_j)\) muestra simetría con respecto a desplazamientos de simetría equivalente a coordenadas cartesianas. Por ejemplo, considere la molécula de agua en su geometría de\(C_{2v}\) equilibrio como se ilustra en la Figura 3.2. Un movimiento muy pequeño del\(H\) átomo izquierdo de la\(H_2O\) molécula en la\(x\) dirección positiva (\(\Delta x_L\)) produce el mismo cambio en el potencial\(V\) que un desplazamiento correspondientemente pequeño del\(H\) átomo derecho en la\(x\) dirección negativa

(\(-\Delta x_R\)). De manera similar, el movimiento de la H izquierda en la dirección y positiva (\(\Delta y_L\)) produce un cambio de energía idéntico al movimiento de la H derecha en la dirección y positiva (\(\Delta y_R\)).

Figura 3.2. Molécula de agua que muestra sus dos longitudes de enlace y ángulo

La equivalencia de los pares de desplazamientos de coordenadas cartesianas es el resultado de que los vectores de desplazamiento están conectados por las operaciones de grupo de puntos del\(C_{2v}\) grupo. En particular, la reflexión\(\Delta x_L\) a través del plano yz (los dos planos se representan en la Figura 3.3) produce\(-\Delta x_R\), y la reflexión de\(\Delta y_L\) a través de este mismo plano cede\(\Delta y_R\).

Figura 3.3. Dos planos de simetría de la molécula de agua.

De manera más general, es posible combinar conjuntos de coordenadas de desplazamiento cartesiano {\(q_k\)} en las llamadas coordenadas adaptadas a simetría {\(Q_{\Gamma_j}\)}, donde el índice\(\Gamma\) etiqueta la representación irreducible en el grupo de puntos apropiado y j etiqueta la combinación particular de esa simetría ( es decir, puede haber más de un tipo de desplazamiento que tenga una simetría dada G). Estas coordenadas adaptadas a la simetría se pueden formar aplicando los operadores de proyección de grupos de puntos (que se tratan en detalle en el Capítulo 4) a las coordenadas individuales de desplazamiento cartesiano.

Para ilustrar, nuevamente considere la\(H_2O\) molécula en el sistema de coordenadas descrito anteriormente. Las coordenadas\(3N = 9\) de desplazamiento cartesiano ponderadas en masa (\(X_L, Y_L, Z_​L, X_O, Y_O, Z_O, X_R, Y_R, Z_R​\)) se pueden adaptar a la simetría aplicando los siguientes cuatro operadores de proyección:

\[P_{A_1} = 1 + \sigma_{yz} + \sigma_{xy} + C_2 \]

\[P_{b_1} = 1 + \sigma_{yz} - \sigma_{xy} - C_2 \]

\[P_{​b_2} = 1 - \sigma_{yz} + \sigma_{xy} - C_2 \]

\[P_{​a_2} = 1 - \sigma_{yz} - \sigma_{xy} + C_2 \]

a cada una de las 9 coordenadas originales (el símbolo s denota reflexión a través de un plano y\(C_2\) significa rotación alrededor del\(C_2\) eje de la molécula). Por supuesto, no se obtendrán 9 x 4 = 36 coordenadas independientes adaptadas a simetría de esta manera; surgirán muchas combinaciones idénticas, y solo 9 serán independientes.

Las combinaciones independientes de\(a_1\) simetría (normalizadas para producir vectores de longitud unitaria) son

\[Q_{a_1,1} = \dfrac{1}{\sqrt{2}} [X_L- X_R]\]

\[Q_{​a_1,2} = \dfrac{1}{\sqrt{2}} [Y_L + Y_R]\]

\[Q_{​a_1,3} = [Y_O]\]

Los de\(b_2\) simetría son

\[Q_{​b_2,1} = \dfrac{1}{\sqrt{2}} [X_L+ X_R]\]

\[Q_{​b_2,2} = \dfrac{1}{\sqrt{2}} [Y_L - Y_R]\]

\[Q_{​b_2,3} = [X_O],\]

y las combinaciones

\[Q_{​b_1,1} = \dfrac{1}{\sqrt{2}} [Z_L + Z_R]\]

\[Q_{​b_1,2} = [Z_O]\]

son de\(b_1\) simetría, mientras que

\[Q_{a_2,1} = \dfrac{1}{\sqrt{2}} [Z_L - Z_R]\]

es de\(a_2\) simetría.

Grupo de puntos Simetría del Potencial Armónico

Estas nueve coordenadas adaptadas a la simetría\(Q_{\Gamma_j}\) se expresan como transformaciones unitarias de las coordenadas cartesianas originales ponderadas en masa:

\[Q_{\Gamma_j} = C_{\Gamma_{j,k}} X_k \]

Estos coeficientes de transformación\({C_{\Gamma_{j,k}}}\) pueden ser utilizados para llevar a cabo una transformación unitaria de la matriz de Hessian ponderada en masa 9x9. Al hacerlo, solo necesitamos formar bloques

\[H_{\Gamma_{j,l}} = \sum_{k,k’} C_{\Gamma_{j,k}} H_{k,k'} \sqrt{m_k m_{k'}} C_{\Gamma_{l,k'}} \]

dentro del cual las simetrías de los dos modos son idénticas. Los elementos fuera de la diagonal

\[H_{\Gamma_j\Gamma'_l}= \sum_{k,k’} C_{\Gamma_{j,k}} H_{k,k'} \sqrt{m_k m_{k'}} C_{\Gamma'_{l,k'}} \]

desaparecer porque el potencial\(V(q_j)\) (y el hamiltoniano vibracional completo\(H = T + V\)) viaja con las operaciones de simetría del grupo de\(C_{2V}\) puntos.

Como resultado, el problema del valor propio de Hessian ponderado en masa 9x9 se puede subdividir en dos problemas de matriz 3x3 (de\(a_1\) y\(b_2\) simetría), una matriz de\(b_1\) simetría de 2x2 y una matriz de\(a_2\) simetría 1x1. Por ejemplo, el bloque de\(a_1\) simetría His formó de la siguiente manera:

\ [
\ left [\ begin {array} {ccc}
\ dfrac {1} {\ sqrt {2}} & -\ dfrac {1} {\ sqrt {2}} & 0\
\ dfrac {1} {\ sqrt {2}} &\ dfrac {1} {\ sqrt {2}} & 0\\
0 & 0 & 1
\ end {array}\ derecha]
\ izquierda [\ begin {array} {ccc}
m_h^ {-1/2}\ dfrac {\ parcial^2 V} {\ parcial x_l^2} m_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ parcial^2 V} {\ parcial x_l\ parcial x_r} m_H^ {-1/2} & m_H^ {-1/2}\ dfrac {\ parcial ^2 V} {parcial\ x_l\ Y_o parcial} m_h^ {-1/2}\\
m_h^ {-1/2}\ dfrac {\ parcial^2 V} {\ parcial x_r\ parcial x_l} m_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ parcial^2 V} {\ parcial x_r^2} m_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ parcial^2 V} {\ parcial x_r\ parcial Y_o} m_h^ {-1/2}\
m_h^ {-1/2}\ dfrac {\ parcial^2 V} {\ Y_o parcial\ parcial x_l} m_h^ ^ {-1/2} & m_H^ {-1/2}\ dfrac {\ parcial^2 V} {\ Y_o parcial\ parcial x_R} m_h^ {-1/2} & m_H^ {-1/2}\ dfrac {\ parcial^2 V} {\ Y_o^2} M_h^ {-1/2}
\ end {array}\ derecha]
\ izquierda [\ begin {array} {ccc}
\ dfrac {1} {\ sqrt {2}} &\ dfrac {1} {\ sqrt {2}} & 0\
-\ dfrac {1} {\ sqrt {2}} &\ dfrac {1} {\ sqrt {2}} & 0\\
0 & 0 & 1
\ end {array}\ derecha]
\]

Los\(a_2\) bloques\(b_2\),\(b_1\) y se forman de manera similar. Los valores propios de cada uno de estos bloques proporcionan los cuadrados de las frecuencias vibracionales armónicas, los vectores propios proporcionan los coeficientes\(\{C_{\Gamma_{j,k}}\}\) del modo\(j^{\rm th}\) normal de simetría\(\Gamma\) en términos de las coordenadas cartesianas ponderadas en masa {\(X_k\)}. La relación\(X_k = q_k \sqrt{(m_k)}\) puede entonces ser utilizada para expresar estos coeficientes en términos de las coordenadas cartesianas originales {\(q_k\)}.

Independientemente de si se usa simetría para bloquear diagonalizar el hessian ponderado en masa, seis (para moléculas no lineales) o cinco (para especies lineales) de los valores propios serán iguales a cero. Los vectores propios que pertenecen a estos valores propios cero describen las 3 traducciones y 2 o 3 rotaciones de la molécula. Por ejemplo, cuando se expresa en términos de las coordenadas cartesianas originales (es decir, no ponderadas en masa)

\[\dfrac{1}{\sqrt{3}}[x_L + x_R + x_O]\]

\[\dfrac{1}{\sqrt{3}}[y_L + y_R + y_O]\]

\[\dfrac{1}{\sqrt{3}}[z_L +z_R + z_O]\]

son tres vectores propios de traducción de\(b_2\),\(a_1\) y\(b_1\) simetría, y

\[\dfrac{1}{\sqrt{2}}(z_L-z_R)\]

es una rotación (alrededor del eje y en la Figura 3.2) de\(a_2\) simetría. Este vector de rotación se puede generar aplicando el operador\(a_2\) de proyección a\(z_L\) o a\(z_R\). Las otras dos rotaciones son de\(b_1\) y\(b_2\) simetría e implican el giro de la molécula alrededor de los ejes\(x\)\(z\) - y - de la Figura 3.2, respectivamente.

Entonces, de los 9 desplazamientos cartesianos, 3 son de\(a_1\) simetría, 3 de\(b_2\), 2 de\(b_1\), y 1 de\(a_2\). De estas, hay tres traducciones (\(a_1\),\(b_2\), y\(b_1\)) y tres rotaciones (\(b_2\),\(b_1\), y a2). Esto deja dos vibraciones de\(a_1\) y una de\(b_2\) simetría. Para el\(H_2O\) ejemplo tratado aquí, los tres valores propios distintos de cero del hessian ponderado en masa son, por lo tanto\(a_1\), de\(b_2\), y\(a_1\) simetría. Describen las vibraciones de estiramiento simétricas y asimétricas y el modo de flexión, respectivamente, como se ilustra en la Figura 3.4.

Figura 3.4: Modos de estiramiento simétrico y asimétrico y modo de flexión del agua

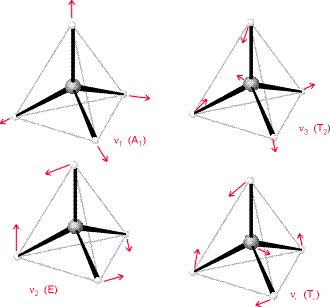
El método de análisis vibracional presentado aquí puede funcionar para cualquier molécula poliatómica. Se conoce el hessian ponderado en masa y luego calcula los valores propios distintos de cero, que luego proporcionan los cuadrados de las frecuencias vibracionales armónicas de los modos normales. La simetría de grupo puntual se puede utilizar para bloquear diagonalizar este hessiano y para etiquetar los modos vibracionales de acuerdo a la simetría como se muestra en la Figura 3.5 para la\(CF_4\) molécula en simetría tetraédrica.

Figura 3.5. Simetrías de vibraciones de metano

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

• Integrated by Tomoyuki Hayashi (UC Davis)