4.6: Teoría de la perturbación dependiente del tiempo
- Page ID
- 70819
Al tratar los efectos de perturbaciones externas (por ejemplo, campos aplicados, colisiones con otras especies), se necesita tener una manera de estimar las probabilidades y tasas de transiciones entre estados del sistema de interés inducidas por estas perturbaciones. La teoría de perturbación dependiente del tiempo (TDPT) ofrece un marco dentro del cual se pueden lograr tales estimaciones.
Derivación
Al derivar las ecuaciones de trabajo de TDPT, se inicia con la ecuación de Schrödinger dependiente del tiempo
\[i\hbar \frac{\partial \Psi}{\partial t}=[H_0+V(t)]\Psi \label{1}\]
en el que\(H_0\) es el hamiltoniano para el sistema cuyas transiciones se van a sondear, y\(V(t)\) es la perturbación causada por el campo externo o la colisión. La función de onda que resuelve esta ecuación se expande de una manera orden por orden como en la teoría de perturbación convencional
\[\Psi=\psi^{(0)}(r)\exp\Big(-it\frac{E^{(0)}}{\hbar}\Big)+\psi^{(1)}+\cdots \label{2}\]
Aquí\(\psi_0\) está la función propia\(H_0\) de la cual se\(H_0\) están considerando las transiciones a otros autoestados (denotados) de. Porque, en ausencia de la perturbación externa\(V(t)\),\(H_0\) se sabe que los estados de varían con el tiempo ya que, este componente de la dependencia temporal de la función de onda total se incluye en la expansión anterior. Luego, la corrección de primer orden\(\psi^{(1)}\) se expande en términos del conjunto completo de estados {} después de lo cual los coeficientes de expansión {} se convierten en las incógnitas a resolver para
\[\psi^{(1)}=\sum_f \psi^{(0)}_f(r)\exp\bigg(-it\frac{E^{(0)}_f}{\hbar}\bigg)C^{(1)}_f(t). \label{3}\]
Cabe señalar que esta derivación trata a los estados de orden cero {\(\psi^{(0)}\)y\(\psi^{(0)}_f\)} como funciones propias de\(H_0\). Sin embargo, en la mayoría de las aplicaciones prácticas de TDPT, {\(\psi^{(0)}\)y\(\psi^{(0)}_f\)} no se conocen exactamente y, de hecho, generalmente se aproximan mediante el uso de métodos variacionales o perturbadores (por ejemplo, para tratar diferencias entre el campo medio de HF y las interacciones coulómbicas verdaderas entre electrones). Entonces, la derivación de TDPT que estamos persiguiendo asume que las {\(\psi^{(0)}\)y\(\psi^{(0)}_f\)} son funciones propias exactas. Cuando se obtienen así las ecuaciones finales de trabajo TDPT, generalmente se sustituyen aproximaciones perturbadoras o variacionales a {\(\psi^{(0)}\)y\(\psi^{(0)}_f\)} en estas ecuaciones.
Sustituir la expansión orden por orden en la ecuación de Schrödinger da, para los lados izquierdo y derecho,
\ [i\ hbar\ frac {\ parcial\ Psi} {\ t parcial} = E^ {(0)}\ psi^ {(0)} (r)\ exp\ Grande (-it\ frac {E^ {(0)}} {\ hbar}\ Grande)\\
+\ sum_f\ izquierda [E^ {(0)} _f\ psi^ {(0)} _f (r)\ exp\ bigg (-it\ frac {E^ {(0)} _f} {\ hbar}\ bigg) C^ {(1)} _f (t)
-i\ hbar\ psi^ {(0)} _f (r)\ exp\ bigg (-it\ frac {E^ {(0)} _f} {\ hbar}\ bigg)\ frac {C^ {(1)} _f (t)} {dt}\ derecha]\ etiqueta {4a}\]
y
\ [[H_0+V (t)]\ Psi=E^ {(0)}\ psi^ {(0)} (r)\ exp\ Grande (-it\ frac {E^ {(0)}} {\ hbar}\ Grande)\\
+\ sum_f E^ {(0)} _f\ psi^ {(0)} _f (r)\ exp bigg (-it\ frac {E^ {(0)} _f} {\ hbar}\ bigg) C^ {(1)} _f (t)
+V (t)\ psi^ {(0)} (r)\ exp\ Grande (-it\ frac {E^ {(0)}} {\ hbar}\ Grande),\ etiqueta {4b}\]
respectivamente, a través de primer orden. Multiplicar cada una de estas ecuaciones a la izquierda por el complejo conjugado de un particular\(\psi_f^0\) e integrarlo sobre las variables de las que\(H_0\) depende produce la siguiente ecuación para los coeficientes de primer orden desconocidos
\[-i\hbar\frac{dC^{(1)}_f(t)}{dt}=\langle \psi^{(0)}_f|V(t)|\psi^{(0)}_f \rangle \exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg). \label{5}\]
Los estados y pueden ser diferentes estados electrónicos, estados vibracionales o estados rotacionales. En el Capítulo 15 de mi libro La Mecánica Cuántica en Química referida en el Capítulo 1, trato con detalle cada uno de estos tipos de transiciones. En la presente discusión, me limitaré al panorama general de TDPT, en lugar de centrarme en cualquiera de estas formas particulares de transiciones espectroscópicas.
Para continuar, hay que decir algo sobre cómo la perturbación\(V(t)\) depende del tiempo. En la aplicación más común de TDPT, se supone que la perturbación consiste en un término que depende de variables espaciales (denotadas\(v(r)\)) multiplicadas por un factor dependiente del tiempo de carácter sinusoidal. Un ejemplo de tal perturbación es proporcionado por el potencial dipolo eléctrico
\[V(t)=\textbf{E}\cdot [ e\sum_n Z_n \textbf{R}_n - e \sum_i \textbf{r}_i ]\cos(\omega t)\]
caracterizar fotones de frecuencia que\(\omega\) interactúan con los núcleos y electrones de una molécula. \(\textbf{E}\cdot [ e\sum_n Z_n \textbf{R}_n - e \sum_i \textbf{r}_i ]\)es la parte espacial\(v(\textbf{r})\) y\(\cos(\omega t)\) es la dependencia del tiempo.
Para permitir la posibilidad de que fotones en un rango de frecuencias puedan incidir sobre las moléculas, podemos proceder con la derivación para fotones de una frecuencia dada\(\omega\) y, después de obtener nuestro resultado final, promediar sobre una distribución de frecuencias caracterizada por una función\(f(\omega)\) que da la número de fotones con frecuencias entre\(\omega\) y\(\omega+d\omega\). Para perturbaciones que no varían de manera sinusoidal (por ejemplo, una perturbación que surge de una colisión con otra molécula), la derivación sigue un camino diferente en este punto (aplicación 3 a continuación). Debido a que las perturbaciones espectroscópicas dependientes del tiempo son extremadamente comunes en la química, centraremos gran parte de nuestra atención en esta clase de perturbaciones en este Capítulo.
Para proceder a derivar las ecuaciones de trabajo de TDPT, la expresión anterior para\(V(t)\) se inserta en la ecuación diferencial para los coeficientes de expansión y la ecuación se integra desde un tiempo inicial\(t_i\) hasta un tiempo final\(t_f\). Estos tiempos describen cuándo se enciende por primera vez la perturbación externa y cuándo se apaga, respectivamente. Por ejemplo, un láser cuyo perfil de intensidad de fotones se describe por\(f(\omega)\) podría ser pulsado de\(t_i\) a\(t_f\), y uno quiere saber qué fracción de las moléculas inicialmente en\(\psi_0\) han sufrido transiciones a cada una de las. Alternativamente, las moléculas pueden estar fluyendo en una corriente que pasa a través de una fuente de luz láser que está continuamente encendida, entrando en el haz láser en\(t_i\) y saliendo del haz láser en\(t_f\). En cualquier caso, las moléculas estarían expuestas a los fotones desde\(t_i\) hasta\(t_f\). El resultado de integrar la ecuación diferencial es
\ [\ begin {split} C^ {(1)} _f (t) &=\ frac {-1} {2i\ hbar}\ int_ {t_i} ^ {t_f}\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ rangle
[\ exp (i\ omega t) +\ exp (-i\ omega t)]\ exp\ bigg (-it\ frac {(E^ {(0)} -E^ {(0)} _f)} {\ hbar}\ bigg)\\
&=\ frac {-1} {2i\ hbar}\ int_ {t_i} ^ {t_f}\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ rangle
[\ exp (i (\ omega+\ omega_ {f,0}) t) +\ exp (-i (\ omega-\ omega_ {f,0}) t)]\
&=\ frac {-1} {2i\ hbar}\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ rangle\\
&\ veces\ izquierda [\ frac {\ exp (i (\ omega+\ omega_ {f,0}) t_f-\ exp (i (\ omega+\ omega_ {f,0}) t_i))} {i (\ omega+\ omega_ {f,0 })}
+\ frac {\ exp (-i (\ omega-\ omega_ {f,0}) t_f-\ exp (-i (\ omega-\ omega_ {f,0}) t_i))} {i (\ omega-\ omega_ {f,0})}
\ derecha]\ end {split}\ label {6}\]
donde las frecuencias de transición\(\omega_{f,0}\) están definidas por
\[\omega_{f,0}=\frac{(E^{(0)}-E^{(0)}_f)}{\hbar} \label{7}\]
y\(t\) es el intervalo de tiempo\(t_f –t_i\).
Ahora bien, si la frecuencia\(\omega\) es cercana a una de las frecuencias de transición, el término con\((\omega-\omega_{f,0})\) en el denominador será mayor que el término que contiene\((\omega-\omega_{f,0})\). Por supuesto, si tiene una energía mayor que, por lo que se está estudiando estimular la espectroscopia de emisión,\(\omega_{f,0}\) será negativa, en cuyo caso\((\omega+\omega_{f,0})\) dominará el término que contenga. En condiciones de espectroscopia de absorción por resonancia, la expresión anterior para los coeficientes de primer orden se reduce a
\ [C^ {(1)} _f (t) =\ frac {-1} {2i\ hbar}\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ rangle
\ frac {\ exp (-i (\ omega-\ omega_ {f,0}) t_f-\ exp (-i (\ omega-\ omega_ {f,0}) t_i))} {i (\ omega-\ omega_ {f,0})}. \ label {8}\]
El módulo al cuadrado de esta cantidad da una medida de la probabilidad de observar el sistema en estado después de ser sometido a los fotones de frecuencia\(\omega\) por un período de tiempo\(t\).
\ [|C^ {(1)} _f (t) |^2=\ frac {|\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ rangle|^2} {4\ hbar^2}
\ frac {2 [1-\ cos ((\ omega-\ omega_ {f,0}) t)]} {(\ omega-\ omega_ {f,0}) ^2}\\
=\ frac {|\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ rangle|^2} {4\ hbar^2}\ frac {\ sin^2 (1/2 (\ omega- omega_ {f,0}) t)} {(\ omega-\ omega_ {f,0}) ^2}
. \ label {9}\]
La función\(\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}\) se representa en la Figura 4.4 para un valor dado de\(t\) como una función de\(\omega\). Tiene un pico bruscamente alrededor\(\omega = \omega_{f,0}\), decae rápidamente a medida que\(|(\omega - \omega_{f,0})|\) aumenta, y muestra recurrencias de intensidad cada vez más pequeña cuando\((\omega - \omega_{f,0})t\) pasa a través de múltiplos de\(\pi\).
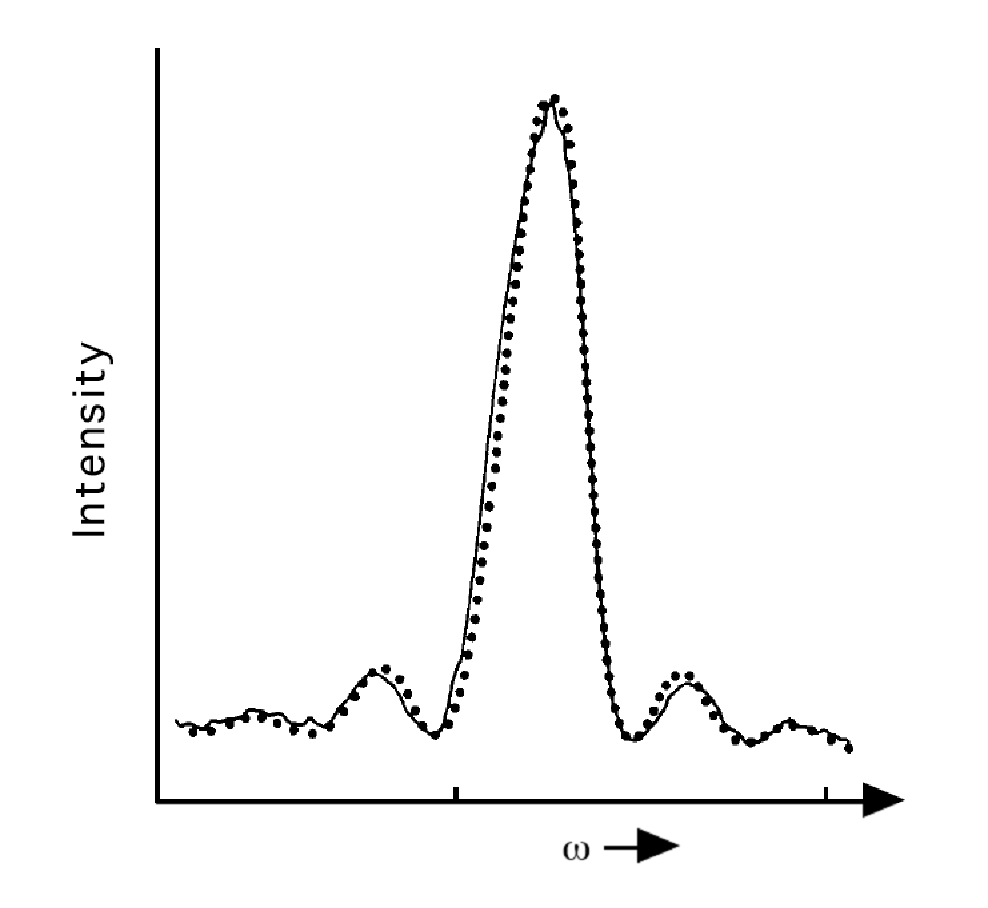
A valores mayores de\(t\), el pico principal en la gráfica de esta función se vuelve cada vez más estrecho y más alto de tal manera que, en el\(t \rightarrow \infty\) límite, el área bajo esta parcela se acerca a\(t\pi/2\):
\[{\rm Area}=\int\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}d\omega=t\frac{\pi}{2}. \label{10}\]
La importancia de esta observación sobre el área bajo la parcela mostrada en la Figura 4.4 puede apreciarse volviendo a nuestro resultado
\[|C^{(1)}_f(t)|^2= \frac{|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2} \frac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2} \label{11}\]
e introduciendo el hecho de que la fuente fotónica utilizada para inducir las transiciones que se están estudiando probablemente no sea perfectamente monocromática. Si se caracteriza, como se sugirió anteriormente, por una distribución de frecuencias\(f(\omega)\) que es más amplia que la anchura del pico central grande en la Figura 4.4 (n.b., esto será cierto si la duración del tiempo\(t\) es lo suficientemente larga), entonces cuando promediemos\(f(\omega)\) para obtener un resultado que directamente se relaciona con este tipo de experimento, obtenemos
\ [\ int_ {-\ infty} ^\ infty f (\ omega) |C^ {(1)} _f (t) |^2d\ omega
=\ frac {|\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ rangle|^2} {4\ hbar^2}\ int_ {-\ infty} ^\ infty f (\ omega)\ frac {\ sen ^2 (1/2 (\ omega-\ omega_ {f,0}) t)} {(\ omega-\ omega_ {f,0}) ^2} d\ omega\
\ frac {\ pi|\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f ( r)\ rangle|^2t} {4\ hbar^2} f (\ omega_ {f,0}) =\ langle |C^ {(1)} _f (t) |^2\ rangle
\ etiqueta {12}\]
Se nos permite escribir la integral\(\omega\) como que va de\(-\infty\) a\(+\infty\) porque la función que se muestra en la Figura 4.4 tiene un pico tan brusco alrededor\(\omega_{f,0}\) que extender el rango de integración no hace ninguna diferencia. Se nos permite factorizar la\(f(\omega)\) salida de la integral como f (\(\omega_{f,0}\)) asumiendo que la función\(f(\omega)\) de distribución de la fuente de luz varía muy suavemente (es decir, no cambia mucho) en el estrecho rango de frecuencias alrededor de\(\omega_{f,0}\) donde la función en la Figura 4.4 tiene un pico brusco.
El resultado de esta derivación de TDPT es la expresión anterior para la probabilidad promedio de observar una transición de estado\(\psi_0\) a estado. Esta probabilidad se ve crecer linealmente con la duración del tiempo durante el cual el sistema está expuesto a la fuente de luz. Debido a que llevamos a cabo esta derivación dentro de la teoría de perturbación de primer orden, debemos confiar en este resultado solo en condiciones donde los efectos de la perturbación sean pequeños. En el contexto del ejemplo aquí considerado, esto significa sólo por tiempos cortos. Es decir, deberíamos ver
\[\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2t}{4\hbar^2}f(\omega_{f,0})=\langle |C^{(1)}_f(t)|^2 \rangle \label{13}\]
como expresar la estimación a corto plazo de la probabilidad de una transición de\(\psi_0\) a y
\[{\rm Rate}=\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,0})\]
(obtenido como\(\dfrac{d\langle |C^{(1)}_f(t)|^2 \rangle}{dt}\)) expresando la velocidad inicial de tales transiciones dentro de la aproximación TDPT de primer orden.
Cabe señalar que la expresión de tasa dada anteriormente no será válida si la duración de tiempo t de la perturbación no obedece\(\omega_{f,o} t \gg p\); sólo cuando se cumple esta condición y la función mostrada en la Figura 4.4 se integrará para generar una predicción de probabilidad que crezca linealmente con el tiempo. Entonces, hay que tener cuidado al usar láseres pulsados de muy corta duración para no emplear la expresión de velocidad simplificada dada anteriormente (e.g., 1 eV corresponde a una frecuencia de ca. 2.4 x10 14 s -1, así que para estudiar una transición electrónica de esta energía, se necesita usar una fuente de luz de duración significativamente mayor que\(10^{-14}\) s para hacer uso del resultado simplificado).
Las ecuaciones de trabajo de TDPT, dadas anteriormente, permiten estimar (porque se trata de una teoría de primer orden) las tasas de transición de un estado cuántico a otro inducidas por una perturbación cuya dependencia espacial se caracteriza\(v(r)\) y cuya dependencia temporal es sinusoidal. El mismo tipo de elementos de matriz de acoplamiento\(\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle\) que experimentamos en PT independientes del tiempo gobiernan las reglas de selección e intensidades para estas transiciones, por lo que no es necesario repetir cómo se puede usar la simetría para analizar estas integrales.
Antes de cerrar este tratamiento de TDPT, es útil abordar algunos temas que fueron eludidos en la derivación presentada anteriormente.
Aplicación 1: Acoplamiento a un Continuum
En algunos casos, uno está interesado en las transiciones de un estado inicial particular\(\psi^{(0)}(r)\) a una variedad de estados que existen en un continuo que tiene energías entre\(E^{(0)}_f\) y\(E^{(0)}_f+dE^{(0)}_f\). Esto ocurre, por ejemplo, cuando se trata la fotoionización de un neutro o fotodesprendimiento de un anión; aquí el electrón expulsado existe en una función de onda continua cuya densidad de estados\(\rho(E^{(0)}_f)\) viene dada por las fórmulas discutidas en el Capítulo 2. En tales casos, la expresión dada anteriormente para la tasa se modifica sumando sobre todos los estados finales que tienen energías dentro\(E^{(0)}_f\) y\(E^{(0)}_f+dE^{(0)}_f\). Volviendo a la expresión anterior
\ [\ int\ rho (E^ {(0)} _f)\ frac {\ pi|\ langle\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ rangle|^2} {4\ hbar^2}
\ int_ {-\ infty} ^\ infty f (\ omega)\ frac {\ sin^2 (1/2 (\ omega-\ omega_ {f,0}) t)} {(\ omega-\ omega_ {f,0}) ^2} d\ omega de^ {(0)} _f\ etiqueta {14}\]
usando\( dE^{(0)}_f=\hbar\omega_{f,0}\), y suponiendo que los elementos de la matriz\(\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle\) no varíen significativamente dentro del estrecho rango entre y, uno llega a una expresión de velocidad de
\[{\rm Rate}=\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,0})\rho(E^{(0)}_f) \label{15}\]
que es muy parecido a lo que obtuvimos antes pero ahora contiene la densidad de los estados\(\rho(E^{(0)}_f)\). En algunos experimentos, uno puede no tener un solo estado\(\psi^{(0)}_f(r)\) que pueda absorber luz de una frecuencia dada w; en tal situación, la atenuación de la fuente de luz a esta frecuencia puede ocurrir a través de absorciones de muchos estados\(\psi^{(0)}_f(r)\) iniciales a todos los estados finales posibles cuya energía difiere de la del estado inicial por. En este caso, la expresión correcta para la tasa total de absorción de fotones de energía se obtiene promediando el resultado anterior sobre las probabilidades\(P_i\) de que el sistema esté en varios estados iniciales (que etiquetamos\(\psi^{(0)}_i\)):
\[{\rm Rate}=\sum_i P_i \frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,i})\rho(E^{(0)}_f)\delta(\omega-\omega_{f,i}). \label{16}\]
Aquí la\(\delta(\omega-\omega_{f,i})\) función garantiza que solo los estados\(\psi^{(0)}_i\) y\(\psi^{(0)}_f\) cuyas energías difieran por están permitidos ingresar a la suma. La naturaleza de la probabilidad del estado inicial\(P_i\) depende del tipo de experimento que se esté llevando a cabo. \(P_i\)podría ser una distribución de Boltzmann si los estados iniciales están en equilibrio térmico, por ejemplo.
Aplicación 2: Oscilaciones Experimentales
En la Figura 4.4\(\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}\) se grafica la función para un valor de\(t\) como una función de\(\omega\). También aparecen en esta figura, puntos que representan datos experimentales. Estos datos se obtuvieron al permitir que una corriente de\(HCN\) moléculas fluyera a través de un rayo láser de ancho\(L\) con la frecuencia del láser sintonizada\(\omega\). A partir de la velocidad\(v\) de flujo de la\(HCN\) corriente y el ancho del rayo láser\(L\), se puede determinar la duración durante la cual las moléculas fueron expuestas a la fuente de luz\(t = \dfrac{L}{v}\). Después de que las moléculas salieron del rayo láser, se sondearon para determinar si estaban en estado excitado. Este experimento se repitió para diversos valores de la frecuencia\(\omega\). Luego se graficó la población de estados excitados en función de\(\omega\) para obtener los datos trazados en la Figura 4.4. Este experimento se describe en el texto Molecules and Radiation, J. I. Steinfeld, MIT Press, Cambridge, Mass. (1981). Este tipo de experimento proporcionó una prueba directa de la dependencia de frecuencia oscilatoria observada en la población de estados excitados como se predijo en nuestra derivación de TDPT.
Aplicación 3: Transiciones inducidas por colisión
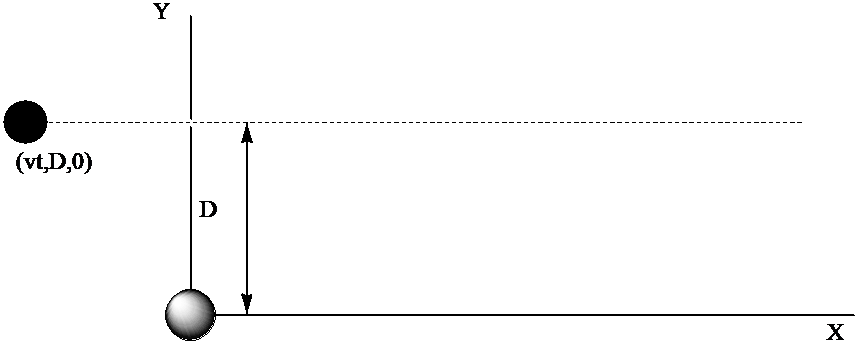
Para dar un ejemplo de cómo se procede en TDPT cuando la perturbación no es oscilatoria en el tiempo, consideremos un átomo ubicado en el origen de nuestro sistema de coordenadas que experimenta una colisión con un ion de carga c cuya trayectoria se describe en la Figura 4.5.
Como aproximación, asumimos
- que el ion se mueve en línea recta:\(= vt, Y = D, Z = 0\), caracterizado por un parámetro de impacto\(D\) y una velocidad\(v\) (esto sería apropiado si el ion se estuviera moviendo tan rápido que no sería desviado por interacciones con el átomo),
- que la perturbación causada por el ion en los electrones del átomo en el origen puede ser representada por
\[-\sum_{i=1}^N\frac{\chi}{|\textbf{r}_i-\textbf{R}|} \label{17}\]
donde\(\textbf{r}_i\) está la posición del i-ésimo electrón en el átomo y\(\textbf{R} = (vt, D, 0)\) es la posición del ion. La dependencia temporal de la perturbación surge del movimiento del ion a lo largo del\(X\) eje.
Escribiendo la distancia\(|\textbf{r}_i-\textbf{R}|\) como
\[|\textbf{r}_i-\textbf{R}|=\sqrt{(x_i-vt)^2+(y_i-D)^2+z_i^2} \label{18}\]
y expandiéndose en potencias inversas de\(\sqrt{D^2+(vt)^2}\) podemos expresar el potencial de interacción ión-átomo como
\[-\sum_{i=1}^N\frac{\chi}{|r_i-R|}=\sum_i^N\left[\frac{-\chi}{\sqrt{D^2+(vt)^2}}+\frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}+\cdots\right]. \label{19}\]
El primer término no contiene factores dependientes de las coordenadas electrónicas del átomo, por lo que no juega ningún papel en provocar transiciones electrónicas. En el segundo término, se\(r_i^2\) puede descuidar\(vtx_i+Dy_i\) el factor en comparación con los términos porque se supone que el ion está algo distante de los electrones de valencia del átomo.
Para derivar una ecuación para la probabilidad de que el átomo experimente una transición de\(\psi^{(0)}(r)\) a\(\psi^{(0)}_f(r)\), se vuelve a la expresión TDPT
\[-i\hbar\frac{dC^{(1)}_f(t)}{dt}=\langle \psi^{(0)}_f|V(t)|\psi^{(0)}(r)\rangle\exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg) \label{20}\]
y sustituye la expresión anterior por la perturbación para obtener
\[\frac{dC^{(1)}_f(t)}{dt}=\frac{-1}{i\hbar} \langle \psi^{(0)}_f|\sum_{i=1}^N \frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}|\psi^{(0)}(r)\rangle \exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg). \label{21}\]
Esta es la ecuación que debe resolverse para evaluar integrando de\(t = -\infty\) a\(t = +\infty\) (representando la colisión completa con el ion comenzando lejos a la izquierda en el\(X\) eje -y procediendo lejos a la derecha).
Hay dos casos limitantes en los que la solución es sencilla. Primero, si el tiempo de duración de la colisión (es decir, el tiempo durante el cual el ion está cerca del átomo)\(\dfrac{D}{v}\) es largo comparado con\(\omega_{f,I}\) donde
\[\omega_{f,0}=\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}, \label{22}\]
entonces el integrando oscilará repetidamente durante el tiempo\(\dfrac{D}{v}\) como resultado de lo cual la integral
\[C^{(1)}_f(t)=\int_{-\infty}^\infty \frac{dC^{(1)}_f(t)}{dt}dt \label{23}\]
va a ser muy pequeño. Entonces, en este llamado caso adiabático (es decir, con el ion moviéndose lentamente con relación a la frecuencia de oscilación\(\omega_{f,0}\)), no se deben esperar transiciones electrónicas. En el otro límite\(\omega_{f,0}\dfrac{D}{v} \ll 1\), el factor\(\exp\bigg(-it\dfrac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg)\) seguirá siendo aproximadamente igual a la unidad, por lo que la integración necesaria reduce a
\[C^{(1)}_f(t)=\frac{-1}{i\hbar}\int_{-\infty}^\infty\langle\psi^{(0)}_f|\frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}|\psi^{(0)}(r)\rangle dt. \label{24}\]
La integral que implica se\(vtx_i\) desvanece porque\(vt\) es impar y el resto del integrando es una función par de\(t\). La integral que implica se\(Dy_i\) puede realizar por sustitución trigonométrica (\(vt = D \tan\theta\)por lo que el denominador reduce\(D^3 \Big(1+\Big(\dfrac{\sin\theta}{\cos\theta}\Big)^2\Big)^{3/2} = \dfrac{D^3}{(\cos\theta)^3}\) y da
\[C^{(1)}_f(t)=\frac{-2\chi}{i\hbar\nu D}\langle\psi^{(0)}_f|\sum_{i=1}^N y_i|\psi^{(0)}(r)\rangle. \label{25}\]
Este resultado sugiere que la probabilidad de una transición
\[|C^{(1)}_f(t)|^2=\frac{4\chi^2}{\hbar^2\nu^2 D^2}|\langle\psi^{(0)}_f|\sum_{i=1}^N y_i|\psi^{(0)}(r)\rangle|^2. \label{26}\]
debe variar según el cuadrado de la carga del ion e inversamente con la velocidad de la colisión. Por supuesto, no se puede confiar en este resultado si la velocidad\(v\) es demasiado baja porque, entonces la condición no\(\omega_{f,0}\dfrac{D}{v} \ll 1\) se mantendrá. Este ejemplo muestra cómo se deben volver a derivar las ecuaciones de TDPT cuando se trata de perturbaciones cuya dependencia del tiempo no es sinusoidal.
Referencias
Para el lector que desee un tratamiento más completo y diverso de TDPT aplicado a la química, sugiero el texto Radiación y Ruido en Electrónica Cuántica, W. H. Louisell, R. E. Krieger, Pub., Huntington, N. Y. (1977) así como mi texto Mecánica Cuántica en Química.
Colaboradores y Atribuciones
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry


