8.1: Herramientas teóricas para estudiar el cambio químico y la dinámica

Teoría del Estado de Transición

El enfoque teórico más exitoso y ampliamente empleado para estudiar las tasas que involucran especies que experimentan reacción en o cerca de condiciones de equilibrio térmico es la teoría del estado de transición (TST) del difunto colega del autor, Henry Eyring. Esta no sería una buena manera de modelar, por ejemplo, reacciones fotoquímicas en las que los reactivos no alcanzan el equilibrio térmico antes de sufrir un progreso significativo de reacción. Sin embargo, para la mayoría de las reacciones térmicas, es notablemente exitosa.

En esta teoría, se ve a los reactivos como sometidos a colisiones que actúan para mantener todos sus grados de libertad (traslacional, rotacional, vibracional, electrónica) en equilibrio térmico. Entre la recolección de tales moléculas reaccionantes, en cualquier instante del tiempo, algunas tendrán suficiente energía interna para acceder a un estado de transición (TS) en la superficie de energía potencial Born-Oppenheimer sobre la que se produce la reacción. Dentro de la TST, la tasa de avance de los reactivos a los productos se expresa entonces en términos de la concentración de especies que existen cerca del TS multiplicada por la velocidad a la que estas especies se mueven a través de la región TS de la superficie energética.

La concentración de especies en el TS está, a su vez, escrita en términos de la expresión constante de equilibrio de la mecánica estadística discutida en el Capítulo 7. Por ejemplo, para una reacción bimolecular\(A+B \rightarrow C\) que pasa a través de un TS denotado AB*, se escribe la concentración (en moléculas por unidad de volumen) de especies AB* en términos de las concentraciones de A y de B y las funciones de partición respectivas como

\[[AB*] = \dfrac{(q_{AB}^*/V)}{(q_A/V)( q_B/V)} [A] [B].\]

Hay, sin embargo, un aspecto de la función de partición de las especies TS que es específico de esta teoría. La función de partición\(q_{AB}^*\) contiene todas las funciones de partición traslacionales, rotacionales, vibracionales y electrónicas habituales que se escribirían, como hicimos en el Capítulo 7, para una molécula AB convencional excepto una modificación. No contiene un

\[\dfrac{\exp(-h\nu_j /2kT)}{1- \exp(-h\nu_j/kT)} \]

contribución vibracional para el movimiento a lo largo de una coordenada interna correspondiente a la trayectoria de reacción.

Figura 8.1 Superficie típica de energía potencial en dos dimensiones mostrando mínimos locales, estados de transición y caminos que los conectan.

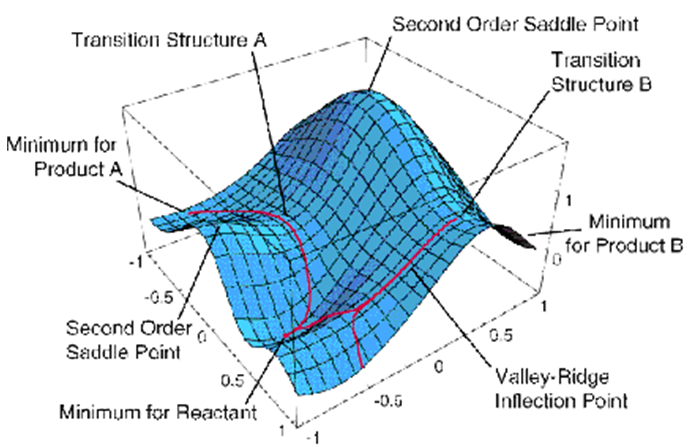
Como se discutió en el Capítulo 3, en las proximidades del TS, la trayectoria de reacción puede identificarse como aquella dirección a lo largo de la cual el PES tiene curvatura negativa; a lo largo de todas las demás direcciones, la superficie de energía está curvada positivamente. Por ejemplo, en la Figura 8.1, una trayectoria de reacción comienza en la Estructura de Transición B y se dirige cuesta abajo. Más específicamente, si uno conoce los gradientes {\((\partial E/\partial q_k)\)} y los elementos de la matriz hessian:

\[H_{j,k} = \dfrac{\partial^2E}{\partial{q_j}\partial{q_k}}\]

de la superficie de energía en el TS, se puede expresar la variación de la energía potencial a lo largo de las coordenadas\(3N\) cartesianas {\(q_k\)} de la molécula de la siguiente manera:

\[E(q_k) = E(0) + \sum_k \dfrac{\partial E}{\partial q_k} q_k + \dfrac{1}{2} \sum_j^k q_j H_{j,k} q_k + …\]

donde E (0) es la energía en el TS, y el {\(q_k\)} denota desplazamientos lejos de la geometría TS. Por supuesto, en el TS, todos los gradientes se desvanecen porque esta geometría corresponde a un punto estacionario. Como se discutió en el Capítulo 3, la matriz de Hessian\(H_{j,k}\) tiene 6 valores propios cero cuyos vectores propios corresponden a la traslación general y rotación de la molécula. Esta matriz tiene valores propios\(3N-7\) positivos cuyos vectores propios corresponden a las vibraciones de las especies TS, así como un autovalor negativo. Este último tiene un vector propio cuyos componentes\(\{q_k\}\) a lo largo de las coordenadas\(3N\) cartesianas describen la dirección de la ruta de reacción a medida que comienza su viaje desde el TS hacia atrás a los reactivos (cuando se sigue en una dirección) y hacia adelante a los productos (cuando se sigue en dirección opuesta). Una vez que se mueve una pequeña cantidad a lo largo de la dirección de curvatura negativa, la trayectoria de reacción es seguida posteriormente por tomar pasos infinitesimales cuesta abajo a lo largo del vector de gradiente\(\textbf{g}\) cuyos\(3N\) componentes son (\(\dfrac{∂E}{∂q_k}\)). Tenga en cuenta que una vez que uno se ha movido cuesta abajo lejos del TS dando el paso inicial a lo largo de la dirección curvada negativamente, el gradiente ya no desaparece porque uno ya no está en el punto estacionario.

Volviendo al cálculo de la tasa de TST, se puede expresar la concentración\([AB^*]\) de especies en el TS en términos de las concentraciones de reactivos y una relación de funciones de partición. El denominador de esta relación contiene las funciones de partición convencionales de las moléculas reaccionantes y puede evaluarse como se discute en el Capítulo 7. Sin embargo, el numerador contiene la función de partición de la especie TS pero con un componente vibracional faltante (es decir:

\[q_{\rm vib} = \prod_{k=1}^{3N-7} \left[\dfrac{\exp(-h\nu_j /2kT)}{1- \exp(-h\nu_j/kT)}\right].\]

Aparte de la que falta\(q_{\rm vib}\), la función de partición del TS también se evalúa como en el Capítulo 7. El movimiento a lo largo de la coordenada de la ruta de reacción contribuye a la expresión de la velocidad en términos de la frecuencia (es decir, con qué frecuencia) con la que el flujo de reacción cruza la región TS dado que el sistema está en equilibrio casi térmico a temperatura\(T\).

Para calcular la frecuencia con la que las trayectorias cruzan el TS y continúan para formar productos, se imagina que el TS consiste en una región estrecha a lo largo de la coordenada de reacción\(s\); el ancho de esta región denotamos\(\delta_s\). A continuación nos preguntamos cuál es el factor de ponderación clásico para que una colisión tenga impulso a\(p_s\) lo largo de la coordenada de reacción. Recordando nuestra discusión de tales asuntos en el Capítulo 7, sabemos que el factor de impulso que entra en la función de partición clásica para la traducción a lo largo de la coordenada de reacción es\((1/h) \exp(-p_s^2/2\mu kT) dp_s\). Aquí, m es el factor de masa asociado a la coordenada de reacción s. Podemos expresar la velocidad o frecuencia a la que dichas trayectorias pasan por la estrecha región de ancho\(\delta_s\) como\(\dfrac{p_s}{\mu\delta_s}\),\(\dfrac{p_s}{\mu}\) siendo la velocidad de paso (cm s ^-1) y\(1/\delta_s\) siendo la inversa de la distancia que define la región TS. Entonces,\(\dfrac{p_s}{\mu\delta_s}\) tiene unidades de s ^-1. En resumen, esperamos que la tasa de trayectorias que se mueven a través de la región TS sea

\[\dfrac{1}{h} \exp\Big(\dfrac{-p_s^2}{2\mu kT}\Big) dp_s \dfrac{p_s}{\mu \delta_s}.\]

Sin embargo, todavía necesitamos integrar esto sobre todos los valores\(p_s\) que corresponden a la energía suficiente\(p_s^2/2m\) para acceder a la energía del TS (relativa a la de los reactivos), que denotamos\(E^*\). Además, tenemos que explicar el hecho de que puede ser que no todas las trayectorias con energía cinética igual\(E^*\) o mayor pasen a formar moléculas de producto; algunas trayectorias pueden pasar por el TS pero luego volver a cruzar la TS y volver a producir reactivos. Además, puede ser que algunas trayectorias con energía cinética a lo largo de la reacción se coordinen menos de lo que\(E^*\) puedan reaccionar por tunelización a través de la barrera.

La forma en que damos cuenta del hecho de que una trayectoria reactiva debe tener al menos\(E^*\) en energía a lo largo de s es integrar sobre solo valores de\(p_s\) mayor que\(\sqrt{2\mu E^*}\). Para dar cuenta del hecho de que algunas trayectorias con energías superiores\(E^*\) pueden volver a cruzarse, incluimos un denominado coeficiente de transmisión k cuyo valor está entre cero y unidad. En el TST más elemental, se ignora la tunelización. Al juntar todas estas piezas, realizamos la integración sobre\(p_s\) recién descrita para obtener:

\[\int\int \dfrac{\kappa}{h} \exp\Big(\dfrac{-p_s^2}{2\mu kT}\Big) \dfrac{p_s}{\mu\delta_s} \delta_s dp_s\]

donde el impulso se integra de\(p_s = \sqrt{2\mu E^*}\) a ∞ y la coordenada s se integra solo sobre la región pequeña\(ds\). Si el coeficiente de transmisión se factoriza fuera de la integral (tratándola como un factor multiplicativo), se\(p_s\) puede evaluar la sobreintegral y arroja lo siguiente:

\[\kappa \dfrac{kT}{h} \exp(\dfrac{-E^*}{kT}).\]

La dependencia exponencial de la energía generalmente se combina con la función de partición de las especies TS que reflejan otras coordenadas\(3N-7\) vibracionales y momentos de esta especie y la velocidad de reacción se expresa como

\[\text{Rate} = \kappa \dfrac{kT}{h} [AB*] = \kappa \dfrac{kT}{h} \dfrac{q_{AB}^* /V}{(q_A/V)( q_B/V)} [A] [B].\]

Esto implica que el coeficiente de velocidad\(k_{\rm rate}\) para esta reacción bimolecular se da en términos de funciones de partición molecular por:

\[k_{\rm rate} = k \dfrac{k_T}{h} \dfrac{q_{AB}^*/V}{(q_A/V)(q_B/V)},\]

que es el resultado fundamental de TST. Una vez más notamos que las relaciones de funciones de partición por unidad de volumen pueden usarse para expresar proporciones de concentraciones de especies (en número de moléculas por unidad de volumen), tal como aparecía en expresiones anteriores para constantes de equilibrio como en el Capítulo 7.

La tasa de expresión anterior solo experimenta modificaciones menores cuando se consideran reacciones unimoleculares. Por ejemplo, en la hipotética reacción\(A \rightarrow B\) vía el TS (\(A^*\)), se obtiene

\[k_{\rm rate} = \kappa \dfrac{kT}{h} \dfrac{q_A^*/V}{q_A/V},\]

donde de nuevo\(q_A^*\) es una función de partición de A* con un componente vibracional faltante.

Antes de poner fin a esta discusión sobre TST, necesito recalcar que esta teoría no es exacta. Se supone que las moléculas reaccionantes están casi en equilibrio térmico, por lo que es menos probable que funcione para reacciones en las que las especies reaccionantes se preparan en condiciones de alto no equilibrio. Además, ignora la tunelización al requerir que todas las reacciones continúen a través de la geometría TS. Para las reacciones en las que se transfiere un átomo de luz (es decir, un átomo de H o D), la tunelización puede ser significativa, por lo que esta forma convencional de TST puede proporcionar errores sustanciales en tales casos (sin embargo, existen aproximaciones directas similares a las que discutimos en el Capítulo 2 que pueden ser utilizadas para hacer túneles correcciones a esta expresión de tasa). Sin embargo, la TST sigue siendo la teoría más utilizada y exitosa de las velocidades de reacción química y se puede extender para incluir túneles y otras correcciones como ahora ilustramos.

Teoría del Estado de Transición Variacional

Dentro de la expresión de TST para la constante de velocidad de una reacción bi-molecular,\(k_{\rm rate} = \kappa\dfrac{kT}{h} \dfrac{q_{AB}^*/V}{(q_A/V)(q_B/V)}\) o de una reacción unimolecular\(k_{\rm rate} = \kappa\dfrac{kT}{h} \dfrac{q_A^*/V}{q_A/V}\), la altura (E^*) de la barrera en la superficie de energía potencial aparece en la función de partición de la especie TS\(q_{AB}^*\) o\(q_A^*\), respectivamente. En particular, la función de partición TS contiene un factor de la forma\(\exp(-E^*/kT)\) en que aparece la energía electrónica Born-Oppenheimer del TS relativa a la de las especies reaccionantes. Esta energía\(E^*\) es el valor de la energía potencial\(E(S)\) en la geometría TS, que denotamos\(S_0\).

Resulta que la aproximación TS convencional para\(k_{\rm rate}\) sobreestimar las velocidades de reacción porque asume que todas las trayectorias que cruzan el TS proceden hacia los productos a menos que se incluya el coeficiente de transmisión para corregir esto. En la teoría del estado de transición variacional (VTST), no se evalúa la relación de funciones de partición que aparecen en\(k_{\rm rate}\) at\(S_0\), sino que primero determina en qué geometría (S*) la función de partición TS (es decir,\(q_{AB}^*\) o\(q_A^*\)) es más pequeña. Debido a que esta función de partición es un producto de (i) el\(\exp(-E(S)/kT)\) factor, así como (ii) 3 funciones de partición traslacionales, 3\(3N-7\) rotacionales y vibracionales (que dependen de\(S\)), el valor\(S\) para el cual este producto es más pequeño no necesita ser el valor TS convencional\(S_0\). Lo que esto significa es que la ubicación (S*) a lo largo de la trayectoria de reacción en la que la energía libre alcanza un punto de silla de montar no es la misma la ubicación\(S_0\) donde la energía electrónica Born-Oppenheimer\(E(S)\) tiene su sillín. Esta interpretación de cómo\(S^*\) y\(S_0\) diferenciarse se puede apreciar recordando que las funciones de partición están relacionadas con la energía libre de Helmholtz\(A\) por\(q = \exp(-A/kT)\); por lo que determinar el valor de\(S\) donde\(q\) alcanza un mínimo es equivalente a encontrar que\(S\) donde la energía libre\(A\) está en un máximo.

Entonces, en VTST, se ajusta la superficie divisoria (a través de la ubicación de la coordenada de reacción S) para encontrar primero ese valor\(S^*\) donde\(k_{\rm rate}\) tiene un mínimo. Luego se evalúan ambos\(E(S^*)\) y los otros componentes de las funciones de partición de la especie TS a este valor\(S^*\). Por último, entonces se utilizan las\(k_{\rm rate}\) expresiones dadas anteriormente, pero con\(S\) tomadas en\(S^*\). Así es como VTST calcula las velocidades de reacción de una manera algo diferente que la TST convencional. Al igual que con TST, el VTST, en la forma señalada anteriormente, no trata la tunelización y el hecho de que no todas las trayectorias que cruzan\(S^*\) proceden a productos. Estas correcciones aún deben incorporarse como un complemento a esta teoría (es decir, en el factor k para recrosar y a través de correcciones de tunelización) para lograr una alta precisión para las reacciones que involucran especies de luz (recuerde del Capítulo 2 que las probabilidades de tunelización dependen exponencialmente de la masa de la tunelización partícula). Refiero al lector a la página web del Prof. Don Truhlar, quien ha sido uno de los pioneros de VTST para mayores detalles.

Trayectoria de reacción Teoría hamiltoniana

Revisemos cuál es el camino de reacción como se definió anteriormente en el Capítulo 3. Es un camino que

1. comienza en un estado de transición (TS) y evoluciona a lo largo de la dirección de curvatura negativa en la superficie de energía potencial (como se encuentra al identificar el vector propio de la matriz de Hessian\(H_{j,k} = \dfrac{∂^2E}{∂q_k∂q_j}\) que pertenece al valor propio negativo);
2. se mueve más cuesta abajo a lo largo del vector de gradiente\(\textbf{g}\) cuyos componentes son\(g_k = \dfrac{∂E}{∂q_k}\),
3. termina en la geometría de los reactivos o productos (dependiendo de si uno comenzó a alejarse del TS hacia adelante o hacia atrás a lo largo de la dirección de curvatura negativa).

Los pasos individuales a lo largo de la coordenada de reacción pueden marcarse\(S_0\)\(S_1\)\(S_2\),,,... a\(S_P\) medida que evolucionan del TS a los productos (etiquetado S_P) y\(S-R\)\(S-R+1\),,... a\(S_0\) medida que evolucionan de los reactivos (S-R) al TS. Si estos pasos se toman en longitudes muy pequeñas (infinitesimales), forman un camino continuo y una coordenada continua que etiquetamos\(S\).

En cualquier punto\(S\) a lo largo de una ruta de reacción, la superficie de energía potencial Born-Oppenheimer\(E(S)\), sus componentes de gradiente

\[g_k(S) = \dfrac{∂E(S)}{∂q_k}\]

y sus componentes de Hessian

\[H_{k,j}(S) = \dfrac{∂^2E(S)}{∂q_k∂q_j}\]

puede evaluarse en términos de derivados de\(E\) con respecto a las coordenadas\(3N\) cartesianas de la molécula. Sin embargo, cuando se realiza una dinámica de trayectoria de reacción, se utiliza un conjunto diferente de coordenadas por razones que son similares a las que surgen en el tratamiento de los modos normales de vibración como se da en el Capítulo 3. En particular, se introducen coordenadas\(3N\) ponderadas en masa\(x_j = q_j \sqrt{m_j}\) que están relacionadas con las coordenadas\(3N\)\(q_j\) cartesianas de la misma manera que vimos en el Capítulo 3.

Las matrices de gradiente y hessian a lo largo de estas nuevas coordenadas {x_j} se pueden evaluar en términos de las contrapartes cartesianas originales:

\[g_{K’}(S) = \dfrac{g_k(S)}{\sqrt{​m_k}}\]

\[ H_{j,k}’ = \dfrac{H_{j,k}}{\sqrt{m_jm_k}}.\]

Entonces se\(H’\) pueden determinar los valores propios {\(\omega_k^2\)\(\textbf{v}_k\)} y los vectores propios {} del hessian ponderado en masa. Al hacerlo, uno encuentra

1. 6 valores propios cero cuyos vectores propios describen la rotación global y la traslación de la molécula;
2. \(3N-7\)valores propios positivos {\(\omega_K^2\)} y vectores propios\(\textbf{v}_K\) a lo largo de los cuales el gradiente\(\textbf{g}\) tiene cero (o casi) componentes;
3. y un valor propio\(\omega_S^2\) (que puede ser positivo, cero o negativo) a lo largo de cuyo vector propio\(\textbf{v}_S\) el gradiente\(\textbf{g}\) tiene su componente más grande.

La única dirección a lo largo\(\textbf{v}_S\) da la dirección de evolución de la trayectoria de reacción (en estas coordenadas ponderadas en masa). Todas las demás direcciones (es decir, dentro del espacio abarcado por los\(3N-7\) otros vectores\(\{\textbf{v}_K\}\)) poseen (casi) componente de gradiente cero y curvatura positiva. Esto significa que en cualquier punto de la ruta\(S\) de reacción que se está discutiendo

1. uno está en o cerca de un mínimo local a lo largo de todas las\(3N-7\) direcciones\(\{\textbf{v}_K\}\) que son transversales a la dirección de la trayectoria de reacción (es decir, la dirección del gradiente);
2. uno puede moverse a un punto vecino en la ruta de reacción moviendo una pequeña cantidad (infinitesimal) a lo largo del gradiente.
3. En términos de las direcciones de modo propio de Hessian\(3N-6\) ponderadas en masa ({\(\textbf{v}_K\)} y\(\textbf{v}_S\)), la superficie de energía potencial puede aproximarse, en la vecindad de cada uno de esos puntos en la trayectoria de reacción\(S\), expandiéndola en potencias de desplazamientos alejados de este punto. Si estos desplazamientos se expresan como componentes\(\delta X_k\) a lo largo de los\(3N-7\) vectores propios\(\textbf{v}_K\) y\(\delta S\) a lo largo de la dirección del gradiente\(\textbf{v}_S\),

se puede escribir la superficie de energía potencial Born-Oppenheimer localmente como:

\[E = E(S) + \textbf{g}\cdot \textbf{v}_S \delta S + \dfrac{1}{2} \omega_S^2 \delta S^2 + \sum_{K = 1}^{3N-7} \dfrac{1}{2} \omega_K^2 \delta X_K^2 .\]

Dentro de esta aproximación cuadrática local, se\(E\) describe una suma de potenciales armónicos a lo largo de cada uno de los\(3N-7\) modos transversales a la dirección de la trayectoria de reacción. A lo largo de la trayectoria de reacción,\(E\) aparece con un gradiente distinto de cero\(\textbf{g}·\textbf{v}_S\) y una curvatura\(\dfrac{1}{2} \omega_S^2\) que puede ser positiva, negativa o cero.

Los modos propios de la hessiana ponderada en masa local (es decir, en la vecindad de cualquier punto\(S\) a lo largo de la ruta de reacción) descomponen las coordenadas\(3N-6\) internas a\(3N-7\) lo largo de las cuales\(E\) es armónica y una (\(S\)) a lo largo de la cual evoluciona la reacción. En términos de estas mismas coordenadas, también se\(T\) puede escribir la energía cinética y así se\(H = T+V\) puede construir la hamiltoniana clásica. Debido a que las coordenadas que utilizamos son ponderadas en masa, en forma cartesiana la energía cinética no\(T\) contiene factores de masa explícitos:

\[T = \dfrac{1}{2} \sum_j m_j \left(\frac{dq_j}{dt}\right)^2 = \dfrac{1}{2} \sum_j \left(\frac{dx_j}{dt}\right)^2.\]

Esto significa que el momento se conjuga a cada coordenada (ponderada en masa)\(x_j\), obtenida de la manera habitual como

\[p_j = ∂[T-V]/∂(\frac{dx_j}{dt}) = \frac{dx_j}{dt},\]

todos tienen factores de masa idénticos (unitarios) asociados a ellos.

Para obtener la expresión de trabajo para la ruta de reacción Hamiltoniana (RPH), se debe transformar la ecuación anterior para la energía cinética\(T\) reemplazando las coordenadas\(3N\) cartesianas ponderadas en masa {\(x_j\)} por

1. las\(3N-7\) coordenadas de desplazamiento de modo propio\(\delta X_j\),
2. la coordenada de desplazamiento de trayectoria de reacción\(\delta S\), y
3. 3 coordenadas de traslación y 3 de rotación.

Las tres coordenadas de traslación se pueden separar e ignorar (porque se conserva la energía del centro de masa) en consideración adicional. Las 3 coordenadas rotacionales no entran en el potencial\(E\), pero sí aparecen en\(T\). Sin embargo, es más común ignorar sus efectos sobre la dinámica que ocurre en las coordenadas internas; esto equivale a ignorar los efectos de las fuerzas centrífugas globales sobre la dinámica de reacción. Procederemos con esta aproximación en mente aunque el lector debe tener en cuenta que hacerlo es una aproximación que uno podría tener que volver a visitar en tratamientos más sofisticados.

Si bien es tedioso realizar la transformación coordinada de los\(T\) señalados anteriormente, se ha hecho en la ponencia W. H. Miller, N. C. Handy y J. E. Adams, Reaction Path Hamiltonian for Polyatomic Molecules, J. Chem. Phys. 72, 99-112 (1980), y resulta en la siguiente forma para el RPH:

\[H = \sum_{K=1}^{3N-7} \dfrac{1}{2}[p_K^2 + \delta X_K^2 \omega_K^2(S)] + E(S) + \dfrac{1}{2} \dfrac{[p_S - \sum_{K,K’=1}^{3N-7} p_K \delta X_{K’} B_{K,K’}]^2}{1+F}\]

donde

\[(1+F) = [1 + \sum_{K=1}^{3N-7} \delta X_K B_{K,S}]^2.\]

A falta de los llamados factores de acoplamiento dinámico\(B_{K,K’}\) y\(B_{K,S}\), esta expresión para\(H\) describe

1. \(3N-7\)armónico-oscilador Hamiltoniano\(\dfrac{1}{2}[p_K^2 + \delta X_K^2\omega_K^2(S)]\) cada uno de los cuales tiene una frecuencia definida localmente\(\omega_K(S)\) que varía a lo largo de la trayectoria de reacción (es decir, es\(S\) -dependiente);
2. un Hamiltoniano\(\dfrac{1}{2} p_S^2 + E(S)\) para el movimiento a lo largo de la coordinación de reacción\(S\) con\(E(S)\) servir como potencial.

En este límite (es decir, con los\(B\) factores apagados), la dinámica de reacción se puede simular en lo que se denomina una manera vibracionalmente adiabática por

1. colocar cada oscilador transversal en un nivel cuántico\(\textbf{v}_K\) que caracterice la población reaccionante de este modo;
2. asignar un momento inicial\(p_S(0)\) a la coordenada de reacción que es característica de la colisión a simular (por ejemplo,\(p_S(0)\) podría muestrearse a partir de una distribución Maxwell-Boltzmann si una reacción térmica es de interés, o\(p_S(0)\) podría elegirse igual a la energía media de colisión de un haz- experimento de colisión);
3. evolucionando en el tiempo el\(S\) y\(p_S\), la coordenada y el impulso utilizando el hamiltoniano anterior, asumiendo que cada modo transversal permanece en el estado cuántico\(\textbf{v}_K\) que tenía cuando comenzó la reacción.

El supuesto que\(\textbf{v}_K\) queda fijo, razón por la cual este modelo se denomina vibracionalmente adiabático, no quiere decir que el contenido de energía del\(K^{\rm th}\) modo permanezca fijo porque las frecuencias\(\omega_K(S)\) varían a medida que uno se mueve a lo largo de la trayectoria de reacción. Como resultado, la energía cinética a lo largo de la coordenada de reacción\(\dfrac{1}{2} p_S^2\) cambiará tanto porque\(E(S)\) varía a lo largo\(S\) como porque\(\sum_{K=1}^{3N-7} \hbar\omega_K^2(S) [\textbf{v}_K + \dfrac{1}{2}]\) varía a lo largo de S.

Volvamos ahora a la teoría de la RPH en la que se incluyen los acoplamientos dinámicos entre el movimiento a lo largo de la trayectoria de reacción y los modos transversales a la misma. En el RPH completo, los términos\(B_{K,K’}(S)\) acoplan modos\(K\) y\(K’\), mientras que\(B_{K,S}(S)\) acopla el camino de reacción a modo\(K\). Estos acoplamientos expresan cómo la energía puede fluir entre estos diversos grados de libertad. Las formas explícitas para los\(B_{K,S}\) factores\(B_{K,K’}\) y se dan en términos de los vectores propios {\(\textbf{v}_K, \textbf{v}_S\)} de la matriz hessiana ponderada en masa de la siguiente manera:

\[B_{K,K’} = \langle d\textbf{v}_K/dS| \textbf{v}_{K’}\rangle; B_{K,S} = \langle d\textbf{v}_K/dS | \textbf{v}_S\rangle\]

donde las derivadas de los vectores propios {\(d\textbf{v}_K/dS\)} se calculan usualmente tomando los vectores propios en dos puntos vecinos\(S\) y a\(S’\) lo largo de la ruta de reacción:

\[\frac{d\textbf{v}_K}{dS} = \frac{\textbf{v}_K(S’) – \textbf{v}_K(S)}{S’-S}.\]

En resumen, una vez que se ha trazado una ruta de reacción, se puede calcular, a lo largo de esta ruta, la matriz de hessiana ponderada en masa y el potencial\(E(S)\). Dadas estas cantidades, todos los términos en el RPH

\[H = \sum_{K=1}^{3N-7} \dfrac{1}{2}[p_K^2 +\delta X_K^2 \omega_K^2(S)] + E(S) + \dfrac{1}{2} \frac{p_S - \sum_{K,K’=1}^{3N-7} p_K \delta X_{K’} B_{K,K’}]^2}{1+F}\]

están en la mano. Este conocimiento puede, posteriormente, ser utilizado para realizar la propagación de un conjunto de coordenadas clásicas y momentos hacia adelante en el tiempo. Para cualquier momento inicial (es decir,\(t = 0\))\(p_S\) y\(p_K\), uno puede usar la forma anterior para H para propagar las coordenadas {\(\delta X_K, \delta S\)} y momenta {\(p_K, p_S\)} hacia adelante en el tiempo. De esta manera, se puede utilizar la teoría de RPH para seguir la evolución temporal de una reacción química que comienza (\(t = 0\)) con coordenadas y momentos característicos de los reactivos bajo condiciones de laboratorio específicas y se mueve a través de un TS y hacia adelante hacia los productos. Una vez que el tiempo ha evolucionado el tiempo suficiente para que se realicen las geometrías del producto, se pueden interrogar los valores de\(\dfrac{1}{2}[p_K^2 + \delta X_K^2 \omega_K^2(S)]\) para determinar cuánta energía se ha depositado en diversas vibraciones producto-molécula y de\(\dfrac{1}{2} p_S^2\) ver cuál es la energía cinética final de los fragmentos de producto. Por supuesto, también se monitorea qué fracción de las trayectorias, cuyas condiciones iniciales se eligen para representar alguna situación experimental, avanza a geometrías de producto vs. regresar a geometrías de reactivos. De esta manera, se puede determinar la probabilidad general de reacción.

Simulación Dinámica Clásica de Tarifas

También se pueden realizar simulaciones dinámicas clásicas de eventos reactivos sin utilizar la ruta de reacción hamiltoniana. Siguiendo un procedimiento como el descrito en el Capítulo 7 donde se discutieron simulaciones clásicas de MD en medios condensados, se pueden evolucionar en el tiempo las ecuaciones de Newton de movimiento de las especies de reacción molecular usando, por ejemplo, las coordenadas cartesianas de cada átomo en el sistema y con un Born-Oppenheimer superficie o una forma funcional parametrizada (por ejemplo, un campo de fuerza). Por supuesto, es esencial que cualquiera que sea la función que se utilice, debe ser capaz de describir con precisión la superficie reactiva, especialmente cerca del estado de transición (recordar, que puede forzar que los campos no lo hagan porque no tienen en cuenta la ruptura y conformación del enlace).

Con cada una de esas coordenadas teniendo una velocidad inicial\((dq/dt)_0\) y un valor inicial\(q_0\), entonces se utilizan las ecuaciones de Newton escritas para un paso de tiempo de duración\(\delta t\) para propagarse\(q\) y\(dq/dt\) reenviar en el tiempo de acuerdo, por ejemplo, con la siguiente fórmula de propagación de primer orden:

\[q(t+\delta t) = q_0 + (dq/dt)_0\delta t\]

\[dq/dt (t+\delta t) = (dq/dt)_0-\delta t[(∂E/∂q)_0/m_q]\]

o usando el algoritmo Verlet descrito en el Capítulo 7. Aquí m_q es el factor de masa que conecta la velocidad dq/dt y el impulso p_q conjugado a la coordenada q:

\[p_q = m_q dq/dt,\]

y\(-(∂E/∂q)_0\) es la fuerza a lo largo de la coordenada\(q\) en la geometría inicial\(q_0\).

Al aplicar el proceso de propagación en el tiempo, se genera un conjunto de nuevas coordenadas\(q(t+\delta t)\) y nuevas velocidades\(dq/dt(t+\delta t)\) apropiadas al sistema en el momento\(t+\delta t\). Usando estas nuevas coordenadas y momentos como\(q_0\)\((dq/dt)_0\) y evaluando las fuerzas\(-(∂E/∂q)_0\) en estas nuevas coordenadas, se pueden usar nuevamente las ecuaciones de Newton para generar otro conjunto de nuevas coordenadas y velocidades de paso finito de tiempo. A través de la aplicación secuencial de este proceso, se genera una secuencia de coordenadas y velocidades que simulan el comportamiento dinámico del sistema.

Al utilizar este tipo de enfoque de trayectoria clásica para estudiar las reacciones químicas, es importante elegir las coordenadas iniciales y los momentos de una manera que sea representativa de las condiciones experimentales que se intenta simular. Las herramientas de la mecánica estadística discutidas en el Capítulo 7 nos guían en la toma de estas elecciones y nos permiten métodos eficientes (por ejemplo, la técnica de Monte Carlo) para muestrear dichos valores iniciales. Cuando se intenta, por ejemplo, simular las colisiones reactivas de un átomo A con una molécula BC para producir AB + C, no es apropiado considerar una sola colisión clásica (o quantal) entre A y BC. ¿Por qué? Porque en cualquier entorno de laboratorio,

1. Los átomos A probablemente se están moviendo hacia las moléculas BC con una distribución de velocidades relativas. Es decir, dentro de la muestra de moléculas (que probablemente contiene 10 ¹⁰ o más moléculas), algunos pares A + BC tienen bajas energías cinéticas relativas cuando chocan, y otros tienen energías cinéticas relativas más altas. Existe una distribución de probabilidad\(P(E_{KE})\) para esta energía cinética relativa que debe ser muestreada adecuadamente en la elección de las condiciones iniciales.
2. Las moléculas BC pueden no estar todas en el mismo estado rotacional (\(J\)) o vibracional (\(v\)). Existe una función de distribución de probabilidad\(P(J,v)\) que describe la fracción de moléculas BC que se encuentran en un\(J\) estado particular y un\(v\) estado particular. Se debe seleccionar un conjunto de valores iniciales de la coordenada vibratoria interna y el momento de la molécula BC, así como su orientación y momento angular rotacional para representar esto\(P(J,v)\).
3. Cuando las moléculas A y BC chocan con un vector de velocidad de movimiento relativo\(v\), no todas golpean de cabeza. Algunas colisiones tienen un parámetro de impacto pequeño\(b\) (la distancia más cercana de A al centro de masa de BC si la colisión ocurriera sin fuerzas atractivas o repulsivas), y algunas tienen grandes\(b\) valores (ver Figura 8.2). La función de probabilidad para estos parámetros de impacto es\(P(b) = 2\pi bdb\), que es simplemente una declaración del hecho geométrico de que\(b\) los valores más grandes tienen más elemento de volumen geométrico que\(b\) los valores -menores.

Figura 8.2 Coordenadas necesarias para caracterizar una colisión átomo-diatomeas mostrando el parámetro de impacto b.

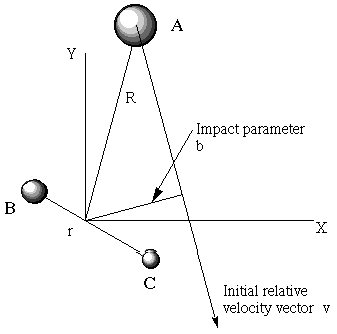
Entonces, para simular todo el conjunto de colisiones que ocurren entre átomos A y moléculas BC en varios\(J\),\(v\) estados y teniendo diversas energías cinéticas relativas\(E_{KE}\) y parámetros de impacto b, uno debe:

1. ejecutar trayectorias clásicas (o propagaciones cuánticas) para un gran número de\(J\),\(v\),\(E_{KE}\), y\(b\) valores,
2. con cada trayectoria asignada una ponderación general (o factor de importancia) de

\[P_{\rm total} = P(E_{KE})P(J,v) 2\pi bdb.\]

Después de que se haya realizado tal conjunto de trayectorias representativas de una condición experimental, se dispone de una gran cantidad de datos. Estos datos incluyen el conocimiento de qué fracción de las trayectorias produjo geometrías finales características de los productos, por lo que se puede calcular la probabilidad neta de reacción. Además, el contenido de energía cinética y potencial de los modos internos (vibracionales y rotacionales) de las moléculas del producto puede ser interrogado y utilizado para calcular histogramas dando probabilidades de observar productos en estos estados. Así es como las simulaciones dinámicas clásicas nos permiten estudiar las reacciones químicas y/o la transferencia de energía.

Teoría RRKM

Otra teoría que es particularmente adecuada para estudiar reacciones de descomposición unimolecular lleva el nombre de los cuatro científicos que la desarrollaron: Rice, Ramsperger, Kassel y Marcus. Para usar esta teoría, se imagina un conjunto de moléculas que han sido activadas a un estado en el que poseen una cantidad total especificada de energía interna\(E\) de la cual\(E^*_{\rm rot}\) existe una cantidad como energía rotacional y el resto como energía vibratoria interna.

El mecanismo por el cual las moléculas se activan podría implicar colisiones o fotoquímica. No importa mientras haya pasado el tiempo suficiente para permitir suponer razonablemente que estas moléculas tienen la energía\(E-E^*_{\rm rot}\) distribuida aleatoriamente entre todos sus grados vibratorios internos de libertad. Al considerar la descomposición unimolecular activada térmicamente de una molécula, las implicaciones de tales supuestos son razonablemente claras. Para los procesos de descomposición unimolecular fotoquímicamente activados, se suele suponer también que la molécula ha sufrido una relajación sin radiación y ha vuelto a su estado electrónico básico pero en una situación bastante vibracionalmente calurosa. Es decir, en este caso, la molécula contiene un exceso de energía vibracional igual a la energía del fotón óptico utilizado para excitarlo. Finalmente, cuando se aplica a reacciones bimoleculares, se asume que la colisión entre los dos fragmentos da como resultado un complejo de larga vida. La vida útil de este intermedio debe ser lo suficientemente larga como para permitir que la energía\(E-E^*_{\rm rot}\), que está relacionada con la energía de colisión de los fragmentos, se distribuya aleatoriamente entre todos los modos vibracionales del complejo de colisión.

Para las reacciones bimoleculares que proceden directamente (es decir, sin formar un intermedio de larga vida), no se emplean teorías de tipo RRKM porque su suposición primaria de aleatorización energética casi con certeza no sería válida en tales casos.

La expresión de RRKM de la constante de velocidad unimolecular para moléculas activadas A* (es decir, ya sea un complejo de larga vida formado en una colisión bimolecular o una molécula caliente) que se disocia a productos a través de un estado de transición,\(A* \rightarrow TS \rightarrow P\), es

\[k_{\rm rate} = \dfrac{G(E-E_0 –E’_{\rm rot})}{N(E-E^*_{\rm rot})h}.\]

Aquí, la energía total\(E\) se relaciona con las energías de las moléculas activadas por

\[E = E^*_{\rm rot} + E^*_{\rm vib}\]

donde\(E^*_{\rm rot}\) está la energía rotacional de la molécula activada y\(E^*_{\rm vib}\) es la energía vibratoria de esta molécula. Esta misma energía\(E\) debe, por supuesto, aparecer en el estado de transición donde se descompone como una cantidad\(E_0\) necesaria para pasar de A* a la TS (es decir, la energía necesaria para alcanzar la barrera) y vibracional (\(E'_{\rm vib})\), traslacional (a\(E'_{\rm trans}\) lo largo de la coordenada de reacción), y rotacional ( \(E'_{\rm rot}\)) energías:

\[E = E_0 + E’_{\rm vib} + E’_{\rm trans} + E’_{\rm rot} .\]

En la expresión del coeficiente de tasa,\(G(E-E_0 –E’_{\rm rot} )\) se encuentra la suma total de estados cuánticos vibracionales internos que posee el estado de transición teniendo energías hasta e incluyendo\(E-E_0 –E’_{\rm rot}\). Esta energía es la energía total\(E\) pero con la energía de activación\(E_0\) eliminada y la energía rotacional general\(E’_{\rm rot}\) del TS eliminada. La cantidad

\(N(E-E^*_{\rm rot})\)es la densidad de los estados cuánticos vibracionales internos (excluyendo el modo que describe la coordenada de reacción) que posee la molécula activada teniendo una energía entre\(E-E^*_{\rm rot}\) y\(E-E^*_{\rm rot} + \delta E\). En esta expresión, la energía\(E-E^*_{\rm rot}\) es la energía total\(E\) con la energía rotacional\(E^*_{\rm rot}\) de las especies activadas removida.

En la versión más comúnmente empleada de la teoría RRKM, se supone que las energías rotacionales de las moléculas activadas\(E^*_{\rm rot}\) y de la TS\(E’_{\rm rot}\) están relacionadas por

\[E^*_{\rm rot} – E’_{\rm rot} = J(J+1) \dfrac{h^2}{8\pi^2} \left(\frac{1}{I^*} - \frac{1}{I’}\right) = E^*_{\rm rot} \left(1 –\frac{I^*}{I’}\right).\]

Aquí\(I^*\) y\(I’\) están los momentos de inercia promedio (tomados sobre los tres valores propios de los tensores de inercia de momento) de las moléculas activadas y especies TS, respectivamente. El supuesto principal encarnado en la relación anterior es que los momentos angulares rotacionales de las especies activadas y TS son los mismos, por lo que sus energías rotacionales pueden relacionarse, tal como se expresa en la ecuación, con cambios en las geometrías reflejados en sus momentos de inercia. Debido a que la teoría RRKM asume que la energía vibracional se distribuye aleatoriamente, su ecuación de coeficiente de velocidad fundamental

\[k_{\rm rate} = \dfrac{G(E-E_0 –E’_{\rm rot} )}{N(E-E^*_{\rm rot})h} \]

depende de la energía total\(E\), la energía\(E_0\) requerida para acceder al TS, y la cantidad de energía contenida en los grados de libertad rotacional que por lo tanto no está disponible para las vibraciones.

Para implementar un cálculo de coeficiente de tasa RRKM, uno debe saber

1. la energía total\(E\) disponible,
2. la energía de barrera\(E_0\),
3. las geometrías (y por lo tanto los momentos de inercia\(I^*\) y\(I’\)) de las moléculas activadas y del TS, respectivamente,
4. la energía rotacional\(E^*_{\rm rot}\) de las moléculas activadas, así como
5. todas las energías\(3N-6\) vibracionales de las moléculas activadas y todas las energías\(3N-7\) vibracionales del TS (es decir, excluyendo la coordenada de reacción).

La energía rotacional de las especies TS puede entonces relacionarse con la de las moléculas activadas a través de

\[E^*_{\rm rot} – E’_{\rm rot} = E^*_{\rm rot} \left(1 –\frac{I^*}{I’}\right).\]

Para simular un experimento en el que las moléculas activadas tienen una distribución térmica de energías rotacionales, se calcula la constante de velocidad RRKM para un rango de\(E^*_{\rm rot}\) valores y luego se promedia sobre el\(E^*_{\rm rot}\) uso de la población térmica de Boltzmann

\[(2J+1) \exp\Big(-J(J+1) \dfrac{h^2}{8\pi^2I^*kT}\Big) \]

como factor de ponderación. Esto se puede llevar a cabo, por ejemplo, utilizando el proceso MC para seleccionar\(J\) valores rotacionales. Esto produce entonces una constante de velocidad para cualquier energía total especificada E. Alternativamente, para simular experimentos en los que las especies activadas se forman en colisiones bimoleculares a una energía especificada\(E\), el coeficiente de velocidad RRKM se calcula para un rango de\(E^*_{\rm rot}\) valores con cada uno\(E^*_{\rm rot}\) relacionado al parámetro de impacto colisional\(b\) que discutimos anteriormente. En ese caso, el momento angular de colisión\(J\) se da como\(J = \mu vb\), donde\(v\) está la velocidad de colisión relativa (relacionada con la energía de colisión) y m es la masa reducida de los dos fragmentos colisionantes. Nuevamente\(E^*_{\rm rot} – E’_{\rm rot} = E^*_{\rm rot} \left(1 –\frac{I^*}{I’}\right)\) el uso de la energía rotacional TS puede relacionarse con la de las especies activadas. Finalmente, el coeficiente de tasa RRKM se evalúa promediando el resultado sobre una serie de parámetros de impacto\(b\) (cada uno de los cuales implica un\(J\) valor y por lo tanto un\(E^*_{\rm rot}\)) con\(2\pi bdb\) como factor de ponderación.

La evaluación de la suma de estados\(G(E-E_0 –E’_{\rm rot} )\) y la densidad de estados\(N(E-E^*_{\rm rot})\) que aparecen en la expresión RRKM se suele llevar a cabo utilizando un algoritmo de conteo de estados como el implementado por Beyer y Swinehart en Commun. Assoc. Comput. Machin. 16, 372 (1973). Este algoritmo utiliza el conocimiento de las frecuencias vibracionales\(3N-6\) armónicas de las moléculas activadas y\(3N-7\) las frecuencias del TS y determina cuántas formas se puede distribuir una cantidad dada de energía entre estos modos. Al sumar todas esas distribuciones para la energía que varía de cero a\(E\), el algoritmo determina G (E). Al tomar la diferencia\(G(E+\delta E) – G(E)\), determina\(N(E)\delta E\). El profesor Bill Hase ha sido uno de los primeros pioneros involucrados en la aplicación de la teoría RRKM a los procesos químicos.

Expresiones de función de correlación para tasas

Recordemos del Capítulo 6 que las tasas de absorción de fotones pueden, en ciertas circunstancias, expresarse ya sea en términos de cuadrados de elementos de la matriz dipolar de transición que conectan cada estado inicial\(\Phi_i\) a cada estado final\(\Phi_f\),

\[| \textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2\]

o en términos del promedio de equilibrio del producto de un vector dipolo de transición en el tiempo\(t=0\) punteado en este mismo vector en otro momento\(t\)

\[\sum_i \rho_i \langle \Phi_i | \textbf{E}_0 \cdot \boldsymbol{\mu} \textbf{E}_0 · \boldsymbol{\mu} (t) | \Phi_i \rangle\]

Es decir, estas tasas se pueden expresar ya sea de una manera de estado a estado o en un marco de función de correlación dependiente del tiempo. En el Capítulo 7, se examinó más a fondo este mismo enfoque de función de correlación.

De manera análoga, es posible expresar las constantes de velocidad de reacción química en un lenguaje de dominio de tiempo nuevamente usando funciones de correlación de tiempo. Las expresiones TST (o VTST) y RRKM para la constante\(k_{rate}\) de velocidad implican, a través de las funciones de partición o densidades de estado, los niveles de energía reactiva y estado de transición y las degeneraciones. Estas teorías son, por lo tanto, análogas de las ecuaciones de la tasa de absorción de fotones de

Para establecer la conexión entre las expresiones de función de estado a estado y correlación de tiempo, se puede comenzar con una expresión clásica para la constante de velocidad dada a continuación:

\[k(t)=\frac{1}{Q_r(2\pi \hbar)^L}\int dpdq e^{-\beta H(q,p)} F(p,q) \chi(p,q)\]

Aquí

• \(Q_r\)es la función de partición de la especie reaccionante,
• L es el número de coordenadas y momentos de los que\(H(\textbf{p},\textbf{q})\) depende el hamiltoniano, y
• \(\beta\)es\(1/kT\).

El factor de flujo\(F\) y la probabilidad de reacción\(c\) se definen en términos de una superficie divisoria que podría, por ejemplo, ser un plano perpendicular a la coordenada de reacción\(S\) y ubicado a lo largo de la trayectoria de reacción que se discutió anteriormente en este Capítulo en la Sección 8.1.3. Los puntos en dicha superficie se pueden definir especificando una condición que las coordenadas L {qj} deben obedecer, y escribimos esta condición como

\[f(\textbf{q}) = 0.\]

Los puntos\(f(\textbf{q}) < 0\) que se encuentran donde se clasifican como tendidos en la región reaccionante del espacio de coordenadas, mientras que los que se encuentran en donde\(f > 0\) están en la región del producto. Por ejemplo, si la superficie divisoria se define como un plano perpendicular a la trayectoria de reacción, la función f se puede escribir como:

\[f(\textbf{q}) = (S(\textbf{q}) - S_0).\]

Aquí,\(S\) está la coordenada de reacción (que, por supuesto, depende de todas las\(q\) variables) y\(S_0\) es el valor de\(S\) en la superficie divisoria. Si la superficie divisoria se coloca en el estado de transición sobre la superficie energética,\(S_0\) desaparece porque el estado de transición es entonces, por convención, el origen de la coordenada de reacción.

Entonces, ahora vemos cómo se puede definir la superficie divisoria, pero ¿cómo se construyen el flujo\(F\) y la probabilidad c? El factor de flujo\(F\) se define en términos de la función de superficie divisoria de la\(f(\textbf{q})\) siguiente manera:

\[F(\textbf{p},\textbf{q}) = \frac{d h(f(\textbf{q}))}{dt}\]

\[= \dfrac{dh}{df} \dfrac{df}{dt}\]

\[=\dfrac{dh}{df} \sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt}\]

\[= \delta(f(\textbf{q})) \sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt}.\]

Aquí,\(h(f(\textbf{q}))\) está la función de paso Heaviside (\(h(x) = 1\)\(x>0; h(x) = 0\)if if\(x < 0\)), cuya derivada\(dh(x)/dx\) es la función delta Dirac\(\delta(x)\), y las otras identidades siguen usando la regla de cadena. Cuando la superficie divisoria se define en términos de la coordenada de la ruta de reacción\(S\) como se introdujo anteriormente (es decir,\(f(\textbf{q}) = (S - S_0)\)), el factor\(\sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt}\) contiene solo un término cuando se eligen las coordenadas L {\(q_j\)}, como en la teoría de la trayectoria de reacción, para ser la coordenada de reacción\(S\) y L-1 coordenadas\({q’_j} = q’\) perpendiculares a la trayectoria de reacción. Para tal elección, se obtiene

\[\sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt} = \frac{dS}{dt} = \dfrac{P_S}{m_S}\]

donde\(P_S\) está el impulso a lo largo\(S\) y\(m_S\) es el factor de masa asociado\(S\) en la ruta de reacción hamiltoniana. Entonces, en este caso, el factor de flujo total se\(F\) reduce a:

\[F(\textbf{p},\textbf{q}) = \delta(S-S_0) \dfrac{P_S}{m_S}.\]

Hemos visto exactamente este constructo antes en la Sección 8.1.2 donde se desarrolló la expresión de TST para el coeficiente de tasa.

El factor de probabilidad de reacción\(c(\textbf{p},\textbf{q})\) se define en términos de aquellas trayectorias que evolucionan, a largo tiempo\(t \rightarrow \infty\), sobre el lado del producto de la superficie divisoria; tales trayectorias obedecen

\[c(\textbf{p},\textbf{q}) = \lim_{t \rightarrow \infty} h(f(q(t))) = 1.\]

Este límite de tiempo prolongado puede, a su vez, expresarse en una forma donde vuelva a ocurrir el factor de flujo

\[\lim_{t \rightarrow \infty}​ h(f(q(t)))​=\int_0^\infty \frac{dh(f(q(t)))​}{dt}dt=\int_0^\infty Fdt\]

En esta expresión, el flujo\(F(t)\) pertenece a coordenadas\(q(t)\) y momentos\(p(t)\) en\(t > 0\). Debido a la reversibilidad del tiempo, la integral se puede extender a un rango desde\(t = - \infty\) hasta\(t = \infty\).

El uso de las expresiones para c y para\(F\) como se desarrolló anteriormente en la ecuación para el coeficiente de tasa dada al inicio de esta Sección permite que el coeficiente de tasa\(k(T)\) sea reescrito de la siguiente manera:

\[k(T)=\frac{1}{Q_r(2\pi \hbar)^L}\int dpdq e^{-\beta H(q,p)} F(p,q) \chi(p,q)​\]

\[=\frac{1}{Q_r(2\pi \hbar)^L}\int_{-\infty}^\infty dt\int dpdq e^{-\beta H(q,p)} F(p,q) F(p(t),q(t))​\]

De esta forma, el factor de\(k(T)\) appears as an equilibrium average (represented by the integral over the initial values of the variables \(p\) and \(q\) with the \(Q_r^{-1} (2\pi \hbar)^{-L}​ \exp(-\beta H)\) ponderación constante de velocidad) de la función de correlación de tiempo del flujo\(F\):

Para evaluar la constante de velocidad en este marco de dominio de tiempo para una reacción química específica, se procedería de la siguiente manera.

1. Ejecutar un conjunto de trayectorias cuyas coordenadas iniciales y momentos\({q.p}\) son seleccionados (por ejemplo, usando los métodos de Montecarlo discutidos en el Capítulo 7) a partir de una distribución con\(\exp(-\beta H)\) como su factor de ponderación.
2. Asegúrese de que las coordenadas iniciales se\({q}\) encuentren en la superficie divisoria porque la expresión de flujo contiene el\(\delta(f(\textbf{q})) \) factor;
3. Monitoree cada trayectoria para observar cuándo cruza de nuevo la superficie divisoria (es decir, cuando de\({q(t)}\) nuevo obedece\(f(q(t)) = 0\); momento en el que la cantidad
4. \(F(p(t),q(t))\)se puede evaluar como\(F(\textbf{p},\textbf{q}) = \delta(f(\textbf{q})) \sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt}\), usando las coordenadas y momenta en el momento\(t\) para calcular estas cantidades.

El uso de una superficie divisoria plana unida a la trayectoria de reacción en\(S = S_0\) como se señaló anteriormente\(F(q,p)\) permite calcularse en términos del memento inicial (\(t=0\)) que se extiende a lo largo de la dirección de la trayectoria de reacción como,\(F(\textbf{p},\textbf{q}) = \delta(S-S_0) \dfrac{P_S}{m_S}\) y\(F(p(t),q(t))\) permite ser calculado cuando la trayectoria cruza de nuevo esta superficie en el momento\(t\) como\(F(p(t),q(t)) = \delta(S-S_0) P_S(t)/m_S\). Entonces, todo lo que realmente se necesita si la superficie divisoria se define de esta manera es iniciar trayectorias con\(S = S_0\); hacer un seguimiento del impulso inicial a lo largo\(S\); determinar en qué momentos regresa\(t\) la trayectoria\(S = S_0\); y formar el producto\(\dfrac{P_S}{m_S} \dfrac{P_S(t)}{m_S}\) para cada uno de tales tiempo. Es de esta manera que se pueden calcular las funciones de correlación flujo-flujo y, por lo tanto, el coeficiente de tasa.

Observe que las trayectorias que experimentan re-cruces superficiales contribuyen con términos negativos a la función de correlación flujo-flujo calculada como se discutió anteriormente. Es decir, una trayectoria con un valor inicial positivo de\((\dfrac{P_S}{m_S})\) puede, en algún momento posterior t, cruzar la superficie divisoria con un valor negativo de\(\dfrac{P_S(t)}{m_S}\) (es decir, dirigirse de nuevo hacia los reactivos). Este re-cruce aportará un valor negativo, a través del producto\(\dfrac{P_S}{m_S}\dfrac{P_S(t)}{m_S}\), a la función de correlación total, que se integra en todo momento. Por supuesto, si esta misma trayectoria experimenta posteriormente otro cruce de la superficie divisoria en t' con positivo\(P_S(t')\), aportará un término positivo a la función de correlación vía. \(\dfrac{P_S}{m_S}\dfrac{P_S(t')}{m_S}\). Por lo tanto, el enfoque de función de correlación para calcular el coeficiente de velocidad puede explicar adecuadamente los re-cruces de superficie, a diferencia del TST que requiere uno para tener en cuenta tales efectos en el coeficiente de transmisión k.

Propagación de paquetes de

Las discusiones de los Capítulos 1 y 7 deberían haber dejado claro que es muy difícil propagar en el tiempo las funciones de onda rigurosamente utilizando la mecánica cuántica. Por otro lado, propagar una trayectoria clásica es relativamente sencillo. Además de las herramientas semi-clásicas introducidas en el Capítulo 1, existe otra poderosa herramienta que permite conservar gran parte de la facilidad computacional y la interpretación conveniente del enfoque de trayectoria clásica al tiempo que incorpora efectos cuánticos que son apropiados en ciertas circunstancias. En este enfoque de propagación de paquetes de ondas, se inicia con una función de onda mecánica cuántica que se caracteriza por dos parámetros que especifican el valor promedio de la posición y del impulso a lo largo de cada coordenada. Se propaga entonces no la función de onda cuántica sino los valores de estos dos parámetros, que se supone que evolucionarán de acuerdo con la dinámica newtoniana. Veamos cómo se dan estos pasos con más detalle y tratemos de entender cuándo se espera que ese enfoque funcione o fracase.

Primero, la forma de la llamada función cuántica de paquetes de ondas se escribe de la siguiente manera:

\[Y(q,Q, P) = \prod_{J=1}^N \frac{1}{\sqrt{2\pi\langle \delta q_J^2\rangle}} \exp\Big[\frac{iP_J q_J}{\hbar} -\frac{(q_J - Q_J)^2}{4}\langle \delta q_J^2\rangle \Big].\]

Aquí, tenemos un total de N coordenadas que denotamos {\(q_J : J=1,N\)}. Son estas coordenadas de las que depende la función de onda cuántica. La función de onda total es un producto de términos, uno para cada coordenada. Observe que esta función de onda tiene dos formas distintas en las que\(q_J\) aparece la coordenada. Primero, tiene una dependencia espacial gaussiana (\(\exp\Big[- \dfrac{(q_J - Q_J)^2}{4}\langle \delta q_J^2\rangle \Big]\)) centrada en los valores\(Q_J\) y teniendo factores de ancho gaussiano relacionados con\(\langle q_J^2\rangle \). Esta dependencia tiende a hacer que la amplitud de la función de onda sea más grande cuando\(q_J\) está cerca de\(Q_J\). En segundo lugar, tiene una forma\(\exp\Big[\dfrac{iP_J q_J}{\hbar}\Big]\) que se parece a la onda viajera que encontramos en el Capítulo 1 en la que la coordenada\(q_J\) se mueve con ímpetu\(P_J\). Entonces, estas funciones de paquetes de onda tienen incorporadas en ellas características que les permiten describir el movimiento (via. la\(P_J\)) de una amplitud que se centra en\(Q_J\) con una anchura dada por el parámetro\(\langle q_J^2\rangle \).

En esta aproximación a la dinámica química, asumimos los parámetros\(P_J\) y\(Q_J\) sufriremos una evolución clásica del tiempo de acuerdo con las ecuaciones de Newton:

\[\frac{dQ_J}{dt} = \frac{P_J}{m_J}\]

\[\frac{dP_J}{dt} = - \frac{∂V}{∂Q_J}\]

donde\(V\) está la superficie de energía potencial (Born-Oppenheimer o campo de fuerza) sobre la cual deseamos propagar el paquete de ondas, y\(m_J\) es la masa asociada con la coordenada\(q_J\). Para la forma de la función de onda dada anteriormente, los\(P_J\) parámetros\(Q_J\) y se pueden mostrar como los valores de expectativa de las coordenadas\(q_J\) y momento\(-i\hbar\dfrac{∂}{∂q_J}\):

\[Q_J = \int Y^* q_J Y dq,\]

\[P_J = \int Y^* (- i \hbar\dfrac{∂}{∂q_J}) Y dq.\]

Además, el\(\langle q_J^2\rangle \) parámetro que aparece en la parte gaussiana de la función se puede mostrar para igualar la dispersión o propagación de esta función de onda a lo largo de la coordenada\(q_J\):

\[\langle q_J^2\rangle = \int Y^* (q_J - Q_J)^2 Y dq.\]

Hay una característica importante de las funciones de paquetes de ondas gaussianas anteriores que debemos señalar. Resulta que las funciones de la forma:

\[Y(q,Q(t), P(t)) = \prod_{J=1}^N \frac{1}{\sqrt{2\pi\langle \delta q_J^2\rangle}} \exp\Big[\frac{iP_J(t) q_J}{\hbar} -\frac{(q_J - Q_J(t))^2}{4}\langle \delta q_J^2\rangle \Big]\]

puede demostrarse que tienen incertidumbres en\(q_J\) y en\(- i \hbar\dfrac{∂}{∂q_J}\) cuyo producto es lo más pequeño posible:

\[\langle (q_J –Q_J)^2\rangle \langle (- i \hbar\dfrac{∂}{∂q_J} – P_J)^2\rangle = \dfrac{\hbar^2}{4}.\]

La prueba de que la forma de paquete de onda de la función de onda tiene el producto de incertidumbre más pequeña se da en el libro de texto Quantum Mechanics, 3a ed., L. I. Schiff, McGraw-Hill, Nueva York (1968). La relación de incertidumbre de Heisenberg, que se discute en muchos textos que tratan de la mecánica cuántica, dice que este producto de las dispersiones de coordenadas y momento debe ser mayor o igual a\(\dfrac{\hbar^2}{4}\). En cierto sentido, la función de paquete de onda gaussiana es la función más clásica que se puede tener porque su producto de incertidumbre es lo más pequeño posible (es decir, igual\(\dfrac{\hbar^2}{4}\)). Decimos que esta es la función cuántica más clásica posible porque en la mecánica clásica, tanto la coordenada como el impulso se pueden conocer con precisión. Entonces, cualquier función de onda cuántica que permita que estas dos variables sean menos inciertas es la más clásica.

Para utilizar la propagación de paquetes de ondas para simular un evento de dinámica química, se inicia con un conjunto de coordenadas clásicas iniciales y momenta {\(Q_J(0), P_J(0)\)} así como un ancho\(\langle q_J^2\rangle \) o incertidumbre para cada coordenada. Cada ancho debe elegirse para representar el rango de esa coordenada en el experimento que se va a simular. Por ejemplo, supongamos que uno iba a representar la dinámica de una función de onda que se prepara mediante la absorción de fotones de un estado\(v = 0\) vibracional de la molécula H-Cl desde el estado de tierra 1S a una superficie de energía de estado excitado (\(V(R)\)). Tal situación se describe cualitativamente en la Figura 8.3. En este caso, se podría\(\langle \delta R^2\rangle\) elegir ser el ancho medio de la función de onda del oscilador\(v = 0\) armónico (o Morse)\(\chi_0(R)\) de H-Cl, y tomar\(P(0) = 0\) (porque este es el valor promedio del impulso para\(\chi_0\)) y\(R(0) = R_{\rm eq}\), la longitud del enlace de equilibrio.

Para tales condiciones iniciales, la dinámica newtoniana clásica se utilizaría entonces para propagar el\(Q_J\) y\(P_J\). En el ejemplo H-Cl, introducido anteriormente, esta propagación se realizaría utilizando la superficie de energía en estado excitado\(E\) ya que, para\(t \rangle 0\), se supone que la molécula está sobre esta superficie. La energía total a la que el paquete de onda inicial que entregó a la superficie superior estaría dictada por la energía del fotón utilizado para realizar la excitación. En la Figura 8.3 se muestran dos ejemplos de este tipo.

Una vez que el paquete está en la superficie superior, su posición\(Q\) e impulso\(P\) comienzan a cambiar de acuerdo con las ecuaciones de Newton. Esto, a su vez, hace que el paquete se mueva como se muestra durante varios pasos de tiempo igualmente espaciados en la Figura 8.3 para los dos casos de fotones diferentes. En esos momentos posteriores, la función de onda cuántica se asume, dentro de este modelo, que viene dada por:

\[Y(q,Q(t), P(t)) = \prod_{J=1}^N \frac{1}{\sqrt{2\pi\langle \delta q_J^2\rangle}} \exp\Big[\frac{iP_J(t) q_J}{\hbar} -\frac{(q_J - Q_J(t))^2}{4}\langle \delta q_J^2\rangle \Big].\]

Es decir, se toma como de la misma forma que la función de onda inicial pero simplemente haber movido su centro de\(Q(0)\) a\(Q(t)\) con un impulso que ha cambiado de\(P(0)\) a\(P(t)\).

Figura 8.3 Propagación del paquete de ondas preparado por absorción de dos fotones diferentes.

Cabe señalar que la evolución temporal del paquete de ondas que se muestra en la Figura 8.3 muestra un comportamiento clásico claro. Por ejemplo, a medida que el tiempo evoluciona, se mueve a valores R grandes y su velocidad (como lo demuestran los espaciamientos entre paquetes vecinos para pasos de tiempo iguales) es grande cuando el potencial es bajo y pequeño cuando el potencial es mayor. Como aprendimos en el Capítulo 6, la función de correlación temporal

\[C(t) = \langle Y(q,Q(0),P(0))|Y(q,Q(t),P(t))\rangle \]

se puede utilizar para extraer información espectral por transformación de Fourier. Para el ejemplo H-Cl considerado aquí, esta función de correlación será grande en\(t = 0\) pero disminuirá en magnitud a medida que el paquete de onda\(Y(q,Q(t),P(t))\) se mueva hacia la derecha (en t1, t2, etc.) porque su superposición con\(Y(q,Q(0),P(0))\) se vuelve cada vez más pequeña a medida que evoluciona el tiempo. Esta decadencia\(C(t)\) ocurrirá más rápidamente para el caso de fotones de alta energía porque\(Y(q,Q(t),P(t))\) se mueve hacia la derecha más rápidamente porque el impulso clásico\(P(t)\) crece más rápidamente. Estas dinámicas inducirán depresiones exponenciales en\(C(t)\) (es decir,\(C(t)\) variarán como\(\exp(-t/\tau_1)\)) en tiempos cortos.

De hecho, la decadencia de lo\(C(t)\) discutido anteriormente produce, cuando\(C(t)\) se transforma Fourier, la característica principal de la función de correlación para el caso de fotones de mayor energía donde finalmente ocurre la disociación. En tales espectros de fotodisociación, se observa una forma de línea lorentziana cuyo ancho se caracteriza por la tasa de decaimiento (\(1/\tau_1\)), que, a su vez, se relaciona con la energía total del paquete y la pendiente de la superficie en estado excitado. Esta pendiente determina qué tan rápido\(P(t)\) crece, lo que luego determina qué tan rápido los fragmentos de enlace H-Cl.

En el caso de fotones de menor energía que se muestra en la Figura 8.3, se produce un comportamiento cualitativamente diferente en\(C(t)\) y por lo tanto en el espectro. El movimiento del paquete hacia\(R\) causas más grandes\(C(t)\) para sufrir inicialmente\(\exp(-t/\tau_1)\) decaimiento. Sin embargo, a medida que el paquete se mueve a su punto de inflexión grande-R (poco después del tiempo\(t_3\)), golpea la pared exterior de la superficie donde se refleja. Posteriormente, experimenta movimiento a R más pequeña, volviendo finalmente a su valor inicial de R. Tales recurrencias, que ocurren en escalas de tiempo que denotamos\(\tau_2\), son características del movimiento ligado en contraste con el movimiento directamente disociativo discutido anteriormente. Esta recurrencia hará\(C(t)\) que se logre de nuevo una gran amplitud, pero, posteriormente\(C(t)\) volverá a sufrir\(\exp(-t/\tau_1)\) decaimiento a medida que el paquete se vaya una vez más. Claramente, la función de correlación mostrará una serie de recurrencias seguidas de depresiones exponenciales. La frecuencia de las recurrencias está determinada por la frecuencia con la que el paquete atraviesa desde sus puntos de inflexión internos a externos y de nuevo, que es proporcional a\(1/\tau_2\). Este, por supuesto, es el periodo vibracional del enlace H-Cl. Entonces, en tales casos de movimiento límite, el espectro (es decir, la transformada de Fourier de C (t)) mostrará una serie de picos espaciados por (\(1/\tau_2\)) con la envolvente de tales picos teniendo una anchura determinada por\(1/\tau_1\).

En casos multimodo más complicados (por ejemplo, en moléculas que contienen varias coordenadas), el movimiento periódico del paquete de ondas suele mostrar otra característica que aún no hemos discutido. Consideremos, por simplicidad, un caso en el que sólo se involucren dos coordenadas. Para que el paquete de olas regrese a (o cerca de) su ubicación inicial, debe pasar suficiente tiempo para que ambas coordenadas hayan sufrido una excursión a sus puntos de inflexión y de regreso. Por ejemplo, considere la situación en la que la frecuencia vibratoria de una coordenada es ca. 1000 cm-1 y la de la otra es de 300 cm-1; estos dos modos requieren entonces ca. 1/30 ps y 1/9 ps, respectivamente, para sufrir una oscilación completa. At\(t = 0\), el paquete de onda, que es un producto de dos paquetes,\(\prod_{J=1}^2 \dfrac{1}{\sqrt{2\pi\langle \delta q_J^2\rangle}} \exp\Big[\dfrac{iP_J(t) q_J}{\hbar} -\dfrac{(q_J - Q_J(t))^2}{4}\langle \delta q_J^2\rangle \Big]\), uno para cada modo, produce una C (t) grande. Después de 1/30 ps, la coordenada del primer modo ha vuelto a su ubicación inicial, pero el segundo modo es solo 9/30 del camino a lo largo en su movimiento periódico. Además, después de 1/9 ps, la coordenada del segundo modo ha vuelto a cerca de donde comenzó, pero ahora el primer modo se ha alejado. Entonces, tanto a 1/30 ps como a 1/9 ps, la función de correlación no será grande porque una de las contribuciones de modo a\(C(t) = \langle Y(q,Q(0),P(0)) | Y(q,Q(t),P(t))\rangle\) será pequeña. Sin embargo, después de 1/3 ps, las coordenadas de ambos modos estarán en posiciones para producir un gran valor de C (t); el modo de alta frecuencia habrá sufrido 10 oscilaciones, y el modo de menor frecuencia habrá sufrido 3 oscilaciones. Mi punto al discutir este ejemplo es ilustrar que las moléculas que tienen muchas coordenadas pueden producir espectros que muestran patrones bastante complicados pero que, en principio, pueden estar relacionados con la evolución temporal de estas coordenadas utilizando la conexión de la función de correlación con el espectro.

Por supuesto, existen problemas que surgen al usar la función de paquete de ondas para describir la evolución temporal de una molécula (o cualquier sistema que deba tratarse mediante mecánica cuántica). Una de las limitaciones más importantes del enfoque de paquetes de ondas a tener en cuenta se relaciona con su incapacidad para tratar adecuadamente las reflexiones de onda. Es bien sabido que cuando una ola choca contra una pared dura, es reflejada por la pared. Sin embargo, cuando, por ejemplo, una ola de agua se mueve repentinamente de una región de aguas profundas a una región mucho más superficial, se observa tanto una onda reflejada como una transmitida. En la discusión de resonancias de tunelización dada en el Capítulo 2, también encontramos ondas reflejadas y transmitidas. Además, cuando una ola golpea una barrera que tiene dos o más agujeros o aberturas en ella, se observan frentes de ola que salen de estas aberturas. El problema con la forma más elemental de paquetes de onda presentada anteriormente es que cada paquete contiene solo una pieza. Por lo tanto, no puede romperse en dos o más piezas ya que, por ejemplo, se refleja desde puntos de inflexión o pasa a través de barreras con agujeros. Debido a que tales paquetes de onda no pueden fragmentarse en dos o más paquetes que posteriormente experimentan una evolución dinámica independiente, no son capaces de describir procesos dinámicos que requieren eventos de fragmentación múltiple. Es principalmente por esta razón que los enfoques de paquetes de ondas para simular dinámicas generalmente se restringen al tratamiento de dinámicas de corto tiempo donde es menos probable que ocurra tal fragmentación del paquete de ondas. Los procesos de fotodisociación molecular rápidos como los que discutimos anteriormente son un buen ejemplo de un fenómeno de tan corto tiempo. Ha habido muchos refinamientos del enfoque de paquetes de ondas descrito anteriormente, algunos de los cuales están diseñados para permitir la división de la función de onda. Refiero al lector el trabajo de uno de los pioneros del enfoque de paquetes de ondas dependientes del tiempo, el profesor Eric Heller, para mayor información sobre este tema.

Dinámica de Salto de Superficie

Existen, por supuesto, reacciones químicas y colisiones de transferencia de energía en las que están involucradas dos o más superficies energéticas Born-Oppenheimer (BO). En tales circunstancias, es fundamental contar con las herramientas necesarias para describir las dinámicas acopladas electrónicas y de movimiento nuclear adecuadas a esta situación.

La forma en que se aborda este problema es volviendo a la ecuación de Schrödinger antes de que se hiciera la aproximación de BO de una sola superficie y expresando la función de onda electrónica\(\Psi(\textbf{r}|\textbf{R})\), que depende de las coordenadas electrónicas {\(\textbf{r}\)} y las coordenadas nucleares\(\{R\}\), como:

\[\Psi(\textbf{r}|\textbf{R})=\sum_J a_J(t)\psi_J(\textbf{r}|\textbf{R})\]

Aquí,\(\psi_J(\textbf{r}|\textbf{R})\) puede ser la función de onda electrónica BO perteneciente al estado\(J^{\rm th}\) electrónico, en cuyo caso decimos que estamos utilizando una base adiabática de estados electrónicos. Las\(a_J(t)\) son amplitudes que se relacionarán con la probabilidad de que el sistema esté en la superficie\(J^{\rm th}\) energética. A continuación, asumimos que las coordenadas {\(\textbf{R}(t)\)} de los núcleos experimentan un movimiento clásico de una manera que se especificará con mayor detalle a continuación que nos permita conocer sus ubicaciones y velocidades (o momentos) en cualquier momento\(t\). Esta suposición implica que la dependencia del tiempo de la función de onda anterior se lleva en la dependencia del tiempo de las coordenadas así\(\textbf{R}(t)\) como en las\(a_J(t)\) amplitudes

\[\Psi(\textbf{r}|\textbf{R(t)})=\sum_J a_J(t)\psi_J(\textbf{r}|\textbf{R(t)})\]

A continuación sustituimos esta expansión por la ecuación de Schrödinger dependiente del tiempo

\[i \hbar \dfrac{\partial \psi}{\partial t} = H_0 (\textbf{r}|\textbf{R}(t))\psi\]

donde\(H_0 (\textbf{r}|\textbf{R}(t))\) está el Hamiltoniano electrónico, que depende de las coordenadas nucleares\(R(t)\) y por lo tanto de la variable de tiempo. Luego multiplicamos la ecuación resultante a la izquierda por una de las funciones de onda\(\psi^*K(\textbf{r}|\textbf{R})\) e integramos sobre las coordenadas electrónicas {\(\textbf{r}\)} para obtener una ecuación para las\(a_K(t)\) amplitudes:

\[i\hbar\frac{da_K}{dt}=\sum_J \left[V_K{K,J}(R(t))-i\hbar\langle \psi_K|\dfrac{d\psi_J}{dt}\rangle \right]a_J .\]

Aquí,\(V_{K,J}\) está el elemento electrónico de la matriz hamiltoniana\(\psi_K\) al que se empareja\(\psi_J\). Este conjunto de ecuaciones diferenciales acopladas para las amplitudes se puede resolver numéricamente, por ejemplo, comenzando en\(t_i\) con\(a_K = 1\)\(a_{J\ne K} = 0\) y propagando los valores de las amplitudes hacia adelante en el tiempo.

El siguiente paso es expresar\(\langle \psi_K|d\psi_J/dt\rangle \), utilizando la regla de la cadena, en términos de derivadas con respecto a las coordenadas nucleares {\(\textbf{R}\)} y la tasa de cambio temporal de estas coordenadas:

\[\langle \psi_K|\dfrac{d\psi_J}{dt}\rangle =\sum_b\langle \psi_K|\dfrac{d\psi_J}{d\textbf{R}_b}\rangle \dfrac{d\textbf{R}_b}{dt}\]

Entonces, ahora las ecuaciones para la\(a_K(t)\) lectura son las siguientes:

\[i\hbar\frac{da_K}{dt}=\sum_J \left[V_K{K,J}(R(t))-i\hbar\sum_b \langle \psi_K|\dfrac{d\psi_J}{d\textbf{R}_b}\rangle \dfrac{d\textbf{R}_b}{dt} \right]a_J​ \]

El

\[\langle \psi_K|\dfrac{d\psi_J}{d\textbf{R}_b}\rangle =\textbf{d}_{K,J}(b)\]

se denominan elementos de matriz de acoplamiento no adiabático (para cada par de estados\(K\) y\(J\), son un vector en el espacio de las coordenadas nucleares\(\textbf{R}\)), y son sus magnitudes las que juegan un papel central en la determinación de la eficiencia de los saltos superficiales. A continuación haremos uso de la siguiente propiedad de simetría de estas cantidades, que derivan de la ortogonalidad de la {\(\psi_J\)}

\[\langle \psi_K|\dfrac{d\psi_J}{d\textbf{R}_b}\rangle =\textbf{d}_{K,J}(b)=-\langle \psi_J|\dfrac{d\psi_K}{d\textbf{R}_b}\rangle ^*=-\textbf{d}_{J,K}^*(b)\]

\[\langle \psi_K|\dfrac{d\psi_K}{d\textbf{R}_b}\rangle =0\]

Estos elementos de matriz están cada vez más disponibles en paquetes informáticos de química cuántica y dinámica ampliamente utilizados (aunque su evaluación eficiente sigue siendo un desafío que está siendo objeto de estudio significativo). Cualitativamente, se puede esperar que un acoplamiento sea grande si el movimiento\(\langle \psi_K|d\psi_J/dRa\rangle\) a lo largo de una coordenada hace que una órbita ocupada se distorsione de una manera que produciría una superposición significativa con una órbita adentro\(\psi_K\).\(\psi_J\)

Si las funciones electrónicas {\(\psi_K\)} aparecen en las ecuaciones

\[i\hbar\frac{da_K}{dt}=\sum_J \left[V_K{K,J}(R(t))-i\hbar\sum_b \textbf{d}_{K,J}(b)\dfrac{d\textbf{R}_b}{dt} \right]a_J​ \]

son funciones propias de BO, los elementos fuera de la diagonal\(V_{­­K,J}\) desaparecen y los elementos diagonales son los niveles de energía BO. En este caso, sólo los términos que implican\(d_{K,J}(b)\) generan transiciones entre superficies. Por otro lado, si se elige funciones electrónicas {\(\psi_K\)} que tienen\(d_{K,J}(b)\) valores de fuga, solo los\(V_{K,J}\) términos inducen transiciones entre superficies. Se dice que este último caso involucra el uso de funciones de onda diabática, mientras que el primero involucra funciones de onda adiabática. Para el resto de esta discusión, asumiré que estamos haciendo uso de funciones de onda adiabática (es decir, BO), pero voy a llevar a través de la derivación de una manera que permitirá usar funciones adiabáticas o diabáticas.

Debido a que finalmente uno está interesado en las poblaciones por estar en diversos estados electrónicos, es común refundir las ecuaciones anteriores para las amplitudes\(a_J(t)\) en ecuaciones para los llamados elementos de matriz de densidad

\[\gamma_{K,J}(t)=a_K(t)a_J^*(t)\]

Los elementos diagonales de la\(\textbf{g}\) matriz son las probabilidades de estado mientras que los elementos fuera de la diagonal contienen información sobre las fases de las cantidades complejas {\(a_J\)}. Entonces, en lugar de las ecuaciones para el {\(a_J(t)\)}, se pueden usar las siguientes ecuaciones para el {\(g_{K,J}\)}:

\[i\hbar\frac{d\gamma_{K,J}}{dt}=\sum_L\left\{ \gamma_{L,J}\left[V_{K,L}-i\hbar\sum_b \dfrac{d\textbf{R}_b}{dt} \textbf{d}_{K,J}(b) \right] - \gamma_{K,L}\left[V_{L,J}-i\hbar\sum_b \dfrac{d\textbf{R}_b}{dt} \textbf{d}_{L,J}(b) \right]\right\} ​\]

Estableciendo\(K=J\), entonces es posible derivar una ecuación para la evolución temporal de los elementos diagonales de la matriz de densidad

\[\frac{d\gamma_{K,K}}{dt}=\sum_{L\ne K}X_{K,L}\]

donde

\[X_{K,L}=\frac{2}{\hbar}\Im\{\gamma_{L,K}V_{K,L}\}-2\Re\{\gamma_{L,K}\sum_b \dfrac{d\textbf{R}_b}{dt} \textbf{d}_{K,J}(b)\}\]

Además de calcular las amplitudes (las probabilidades se calculan entonces como\(|a_J|^2 = \gamma_{J,J}\)), a menudo se necesita identificar (utilizando, quizás el tipo de estrategia discutida en el Capítulo 3) la costura en la que se cruzan las superficies de interés. Esto ayuda a centrar la atención en aquellas geometrías cerca de las cuales es más probable que ocurra un salto superficial.

Para utilizar la forma más básica de teoría de salto de superficie, se procede de la siguiente manera:

1. Se inicia con valores iniciales de las coordenadas nucleares {\(\textbf{R}_b\)} y sus velocidades {\(\textbf{R}_b/dt\)} que caracterizan adecuadamente el tipo de colisión o reacción que se desea simular. Por supuesto, hay que utilizar un conjunto de trayectorias con condiciones iniciales elegidas para describir adecuadamente tal situación experimental. Además, se especifica en qué superficie electrónica (digamos la\(K^{\rm th}\) superficie) se encuentra inicialmente el sistema.
2. Para cada conjunto de condiciones iniciales, se propaga una trayectoria clásica que describe la evolución temporal de la {Ra} y {DRa/dt} en esta superficie inicial (\(K^{\rm th}\)).
3. A medida que se propaga la trayectoria clásica, también se propagan las ecuaciones diferenciales acopladas para los elementos de la matriz de densidad con los núcleos moviéndose sobre la superficie de\(K^{\rm th}\) energía
4. Después de cada etapa de propagación de tiempo de duración\(\delta t\), se evalúa la cantidad mostrada anteriormente (estos elementos dan estimaciones para la tasa de cambio de la población del\(K^{\rm th}\) estado debido a las transiciones a otros estados) a partir de la cual se calcula

.

Estas cantidades controlan el cambio fraccionario en la probabilidad de estar en la\(K^{\rm th}\) superficie\(\gamma_{K,K}\) debido a las transiciones de estado\(K\) a estado\(J\). Se utilizan de la siguiente manera. Se elige un número\(0 < x < 1\) aleatorio. Si\(J\) se permite que ocurra\(x < g_{K,J}\) un salto a la superficie; de lo contrario, no se produce ningún lúpulo y el sistema permanece para continuar su evolución temporal sobre la superficie K.

1. 5. Si ocurre un salto, se permite que las coordenadas y los momentos se propaguen ahora en la superficie de\(J^{\rm th}\) energía, donde las fuerzas, por supuesto, serán diferentes, pero con un solo cambio. El componente del vector de velocidad a lo largo del vector de acoplamiento no adiabático se modifica para permitir que la energía electrónica del sistema haya cambiado repentinamente de\(V_K(R)\) a\(V_J(R)\), lo que debe ser compensado por un cambio en la energía cinética de los núcleos para que se conserve la energía total . Si\(V_K(R) > V_J(R)\), esto da como resultado un aumento en la velocidad;\(V_K(R) < V_J(R)\) si produce una disminución en la velocidad. En este último caso, si\(V_K(R)\) se encuentra considerablemente por debajo\(V_J(R)\), podría resultar que simplemente no hay suficiente energía total para acceder a la superficie\(V_J(R)\); en este caso, no se permite que se produzca el lúpulo.
2. 6. Siguiendo la decisión anterior sobre permitir el salto y ajustar la velocidad a lo largo de la dirección del vector, la trayectoria se continúa con el sistema que ahora se propaga en la\(K^{\rm th}\) superficie\(J^{\rm th}\) o, y las ecuaciones diferenciales involucradas continúan propagándose sin cambios que no sean el hecho de que los núcleos pueden (o no) estar evolucionando sobre una superficie diferente. Todo el proceso se repite hasta que la trayectoria alcanza la terminación (por ejemplo, se observa una reacción o extinción, o se alcanza algún límite de tiempo especificado) momento en el que se pueden sondear las propiedades de los productos tal como se reflejan en las coordenadas y velocidades de los núcleos.

La realización de trayectorias de salto de superficie para un conjunto de trayectorias con condiciones iniciales representativas de un experimento genera un conjunto de\(\gamma_{J,J}\) valores finales (es decir, al final de cada trayectoria) cuyos promedios pueden ser utilizados para estimar la probabilidad global de terminar en el\(J^{\rm th}\) estado electrónico. El algoritmo discutido anteriormente es el llamado método de menos interruptores (detallado en J. C. Tully, J. Chem. Phys. 93, 1061 (1990)) fue pionera por el Prof. John Tully. Este algoritmo de salto de superficie sigue siendo uno de los enfoques más utilizados para tratar tales dinámicas de estado acopladas.

Landau-Zener Saltos de Superficie

Existe una versión simplificada del procedimiento de salto de superficie que se acaba de discutir que a menudo se usa cuando se tienen dos superficies electrónicas que se cruzan en una región del espacio que (i) es energéticamente accesible en el experimento que se simula y (ii) se puede ubicar y caracterizar (por ejemplo, en términos de su coordenadas y gradientes de energía) de una manera computacionalmente factible. Para ilustrar, nuevamente consideramos el caso de Al interactuando con\(H_2\), cuyas superficies de energía potencial se reproducen a continuación de la Figura 3.1c.

Figura 8.3a Representación de las superficies de\(^2B_2\) Oppenheimer\(^2A_1\) y Nacido-Oppenheimer que surgen cuando se\(Al (3s^2 3p^1; ^2P)\) combina con\(H_2 (\sigma_g^2; ^1\Sigma_g^+)\) para formar\(AlH_2(^2A_1)\).

Con el modelo Landau-Zener descrito en esta Sección, las trayectorias se propagan en una superficie de energía hasta que se encuentra un punto sobre o muy cerca de la costura (denotado\(\textbf{R}_x(r)\) en la Figura 8.3 a) momento en el que se invoca una ecuación que da la probabilidad de sufrir un salto a la otra superficie. Es el propósito de esta Sección derivar y explicar esta ecuación de Landau-Zener.

En el Capítulo 4, aprendimos que las tasas de transición de un estado (etiquetado\(i\)) a otro (etiquetado\(f\)) a veces se pueden expresar en términos de elementos de matriz de la perturbación que conecta los dos estados de la siguiente manera

\[{\rm Rate}=\delta(\omega-\omega_{f,i})\dfrac{2\pi |\langle \Psi_f^0|v(r)|\Psi_i^0\rangle |^2}{\hbar^2}.\]

Debido a\(\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \) que los elementos de la matriz de acoplamiento tienen unidades de energía, y la\(\delta(\omega-\omega_{f,i})\) función tiene unidades de frecuencia inversa, la expresión de tasa claramente tiene unidades de\(s^{-1}\). En la ecuación de velocidad, se encuentra la energía de la transición inducida por la luz de la energía, y\(v(r)\) es la perturbación debida al operador dipolo eléctrico. Estas velocidades inducidas por fotones pueden verse como relacionadas con transiciones entre dos superficies que se cruzan: (i) una superficie es la del estado inicial más un fotón de energía, y (ii) la segunda es la del estado final sin fotón. En este punto de vista, el fotón eleva el estado de menor energía hacia arriba en energía hasta que cruza el estado superior y luego el operador dipolo efectúa la transición.

Haciendo analogía con el caso de absorción de fotones, consideramos expresar las tasas de transición entre

1. un estado inicial consistente en un estado electrónico multiplicado por un estado que describe el estado vibracional inicial (incluyendo colisional entre fragmentos) y rotacional del sistema,
2. un estado final que consiste en el producto de otro estado electrónico y vibración-rotación

de la siguiente manera

\[{\rm Rate}=\delta(\omega_{f,i})\dfrac{2\pi |\langle \Psi_f^0\chi_f(R)|v(r)|\Psi_i^0\chi_i(R)\rangle |^2}{\hbar^2}.\]

Es decir, usamos la misma expresión de tasa de regla de oro pero sin energía fotónica necesaria para hacer que las dos superficies se crucen. A continuación usamos la identidad

\[\delta(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\exp(ixt)dt\]

escribir

\[\delta(\omega_{f,i})=\delta((\varepsilon_f-\varepsilon_i)/\hbar)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\exp\Big(\frac{i(\varepsilon_f-\varepsilon_i)​t}{\hbar}\Big)dt.\]

que se puede sustituir en nuestra expresión de tasa para obtener

\ [{\ rm Tasa} =\ frac {1} {2\ pi}\ int_ {-\ infty} ^ {\ infty}\ exp\ Grande (\ frac {i (\ varepsilon_f-\ varepsilon_i) t} {\ hbar}\ grande)
\ dfrac {2\ pi\ langle\ psi_f^0\ chi_f (R) |v (r) |\ psi_i^0\ chi_i (R)\ rangle\ langle\ psi_f^0\ chi_f (R) |v (r) |\ psi_i^0\ chi_i (R)\ rangle} {\ hbar^2} dt.\]

Definir dos hamiltonianos de movimiento nuclear, uno por cada superficie de BO,

\[h_{i,f}=T_R+V_{i,f}(R)\]

y asumiendo que las funciones de onda de movimiento nuclear obedecen

\[h_{i,f}\chi_{i,f}(R)=\varepsilon_{i,f}\chi_{i,f}(R)\]

esta expresión se convierte

\[{\rm Rate}=\frac{1}{2\pi}\int_{-\infty}^{\infty}\dfrac{2\pi \langle \Psi_f^0\chi_f(R)|v(r)|\Psi_i^0\chi_i(R)\rangle \langle \Psi_f^0\chi_f(R)\exp\Big(\dfrac{ih_ft}{\hbar}\Big)|v(r)|\exp\Big(-\dfrac{ih_ft}{\hbar}\Big)\Psi_i^0\chi_i(R)\rangle }{\hbar^2}dt.\]

En la expresión

\[\exp\Big(\dfrac{ih_ft}{\hbar}\Big)|v(r)|\exp\Big(-\dfrac{ih_ft}{\hbar}\Big)\]

los\(\langle \psi_i^0(r)|v(r)|\psi_i^0(r)\rangle \) elementos de\(v(r)\) para nuestro problema de salto superficial implicarían ya sea los acoplamientos Hamiltonianos\(V_{­i,f}\) electrónicos (si se usa una base diabática) o los elementos de acoplamiento no adiabáticos (si se usa una base adiabática BO). En cualquier caso, estos elementos son funciones de las coordenadas nucleares y por lo tanto no se desplazan con los operadores diferenciales que aparecen en\(T_R\). Como resultado, la combinación de operadores\(\exp\Big(\dfrac{ih_ft}{\hbar}\Big)|v(r)|\exp\Big(-\dfrac{ih_ft}{\hbar}\Big)\) debe manejarse con cuidado (por ejemplo, como lo hace uno en la expansión de cluster acoplado tratada en el Capítulo 6) expandiendo los operadores exponenciales y haciendo un seguimiento del hecho de que no todos los términos conmutan. El término de orden más bajo en la expansión de esta combinación de operadores es

\[\exp\Big(\dfrac{ih_ft}{\hbar}\Big)|v(r)|\exp\Big(-\dfrac{ih_ft}{\hbar}\Big)\approx v(r)\exp\Big(\dfrac{it(V_f(\textbf{R})-V_i(\textbf{R}))}{\hbar}\Big)\]

lo que arroja la aproximación que ahora quiero perseguir.

El uso de esta aproximación en nuestra expresión para la tasa de transiciones de salto de superficie da

\[{\rm Rate}=\frac{1}{2\pi}\int_{-\infty}^{\infty}\dfrac{2\pi \langle \Psi_f^0\chi_f(R)|v(r)|\Psi_i^0\chi_i(R)\rangle \langle \chi_f(R)\exp(iV_ft/\hbar)\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \exp(-iV_it/\hbar)\chi_i(R)\rangle }{\hbar^2}dt.\]

Ahora usamos

\[\delta(V_f(\textbf{R})-V_i(\textbf{R}))=\frac{1}{2\pi}\int_{-\infty}^{\infty}\exp\Big(\frac{i(V_f(\textbf{R})-V_i(\textbf{R}))​t}{\hbar}\Big)dt\]

para escribir la tasa como

\[{\rm Rate}=\frac{2\pi}{\hbar} \langle \chi_f(R)\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \chi_i(R)\rangle \langle \chi_f(R)\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \delta(V_f(\textbf{R})-V_i(\textbf{R}))\chi_i(R)\rangle ​.\]

\[=\frac{2\pi}{\hbar}\langle \chi_f(R)|v_{f,i}|\chi_i(R)\rangle \langle \chi_f(R)|v_{f,i}|\delta(V_f(\textbf{R})-V_i(\textbf{R}))\chi_i(R)\rangle ​​\]

donde definimos las integrales de transición electrónica en taquigrafía como

\[v_{f,i}=\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \]

Debido a la función d conservadora de energía, podemos simplificar aún más esta expresión sumando el conjunto completo de las funciones de vibración-rotación del estado final y haciendo uso de la relación de integridad

\[\sum_f\chi_f(R)\chi_f^*(R)=\delta(R-R')\]

para obtener

\[{\rm Rate}=\frac{2\pi}{\hbar}\langle \chi_i(R)|v_{f,i}^*v_{f,i}|\delta(V_f(\textbf{R})-V_i(\textbf{R}))\chi_i(R)\rangle .\]

Se puede ver que esta expresión tiene unidades de s ^-1 ya que la función delta tiene unidades de energía inversa y cada integral de acoplamiento electrónico tiene unidades de energía.

En la expresión de tasa anterior, vemos una función d que limita la integración solo a aquellas geometrías para las cuales\(V_­i = V_f\); estas son las geometrías que se encuentran en la costura de intersección. Cualquier geometría se\(\textbf{R}\) puede expresar en términos de la geometría\(\textbf{S}\) del punto en la costura más cercano a\(\textbf{R}\) más un desplazamiento de magnitud a\(\eta\) lo largo del vector unitario normal a la costura en el punto\(\textbf{S}\)

\[\textbf{R}=\textbf{S}+\hat{\textbf{n}}\eta.\]

Si ahora ampliamos la diferencia de energía\(V_f(\textbf{R}) – V_i(\textbf{R})\) en una serie de Taylor sobre el punto\(\textbf{S}\) que se encuentra en la costura, obtenemos

\[V_f(\textbf{R}) – V_i(\textbf{R})=V_f(\textbf{S}) – V_i(\textbf{S})+\nabla[V_f(\textbf{R}) – V_i(\textbf{R})]_S\bullet\hat{n}(\textbf{S})\eta+\text{ higher - order}\]

El gradiente\(\nabla[V_f(\textbf{R}) – V_i(\textbf{R})]_S\) de la diferencia de potencial tiene cero componentes dentro del subespacio de la costura; su único componente que no desaparece se encuentra a lo largo del\(\hat{n}(\textbf{S})\) vector normal. Ahora usando

\[\delta(ax)=\frac{1}{|a|}\delta(x),\]

la\(\delta(V_f(\textbf{R}) – V_i(\textbf{R}))\) función se puede expresar como

\[\delta(V_f(\textbf{R}) – V_i(\textbf{R}))=\delta((V_f(\textbf{S}) – V_i(\textbf{S}))+\eta\nabla(V_f(\textbf{S}) – V_i(\textbf{S}))\bullet\hat{n}(\textbf{S})+\cdots)\]

\[=\delta(0+\eta\nabla(V_f(\textbf{S}) – V_i(\textbf{S}))\bullet\hat{n}(\textbf{S})+\cdots)=\frac{1}{|\nabla(V_f(\textbf{S}) – V_i(\textbf{S}))\bullet\hat{n}(\textbf{S})|}\delta(\eta)\]

con el\(\delta(h)\) factor que limita la integral para que se encuentre dentro de la costura.

\[{\rm Rate}=\frac{2\pi}{\hbar}\int\int \chi_i^*(R)v_{i,f}^*v_{i,f}\frac{\delta(\eta)}{|\nabla(V_f-V_i)|_S}\chi_i(R)dSd\eta\]

\[=\frac{2\pi}{\hbar}\int \chi_i^*(S,0)v_{i,f}^*v_{i,f}\frac{1}{|\nabla(V_f-V_i)|_S}\chi_i(S,0)dS\]

Este resultado puede interpretarse de la siguiente manera:

1. \(\chi_i^*(S,0)\chi_i(S,0)\)da la densidad de probabilidad para estar en un punto\(\textbf{R}=(\textbf{S},0)\) de la costura; este factor tiene unidades de (longitud) ^{- (3N-6)}.
2. \(\dfrac{2\pi}{\hbar}v_{i,f}^*v_{i,f}\dfrac{1}{|\nabla(V_f-V_i)|_S}\)da la tasa de transiciones de una superficie a otra en el punto\(\textbf{S}\) de la costura; este factor tiene unidades de longitud por s ^-1.
3. El\(d\textbf{S}\) factor tiene unidades de (longitud) ^3N-7; por lo que toda la expresión tiene unidades de s ^-1 como debería.

De esta forma, la expresión de velocidad puede ser utilizada por (i) muestreo (por ejemplo, usando Monte Carlo) sobre la mayor parte de la costura que sea energéticamente accesible, usando la densidad de probabilidad espacial del estado inicial como factor de ponderación, y (ii) formando el promedio de muestreo de la cantidad de tasa\(\dfrac{2\pi}{\hbar}v_{i,f}^*v_{i,f}\dfrac{1}{|\nabla(V_f-V_i)|_S}\) calculada para cada geometría aceptada.

Hay otra manera de utilizar la expresión de velocidad anterior. Si pensamos en un enjambre de\(N\) trayectorias (es decir, un conjunto representativo del experimento de interés) y preguntamos cuál es la velocidad\(r(\textbf{S})\) a la que las trayectorias pasan por una región estrecha de espesor\(\eta\)\(\textbf{S}\) en un punto de la costura, podríamos escribir

\[r(\textbf{S})=N|\chi_i(\textbf{S},\eta)|^2\frac{v_n}{\eta}d\textbf{S}d\eta\]

donde\(|\chi_i(\textbf{S},\eta)|^2\) da la densidad de probabilidad para una trayectoria que está en el punto\(\textbf{S}\) de la costura y que se encuentra dentro de una distancia\(\eta\) a lo largo de la dirección\(\hat{n}(\textbf{S})\) normal a la costura. La cantidad\(\dfrac{v_n}{\eta}\) es el componente de la velocidad a lo largo\(\hat{n}(\textbf{S})\) de la cual el sistema se mueve a través de la costura dividido por el grosor\(\eta\). Esta relación da la inversa del tiempo que el sistema pasa dentro de la\(\eta\) región delgada o, equivalentemente, la frecuencia de pasar por la tira delgada de la costura en S. La cantidad\(d\textbf{S}d\eta\) es el elemento de volumen\(d\textbf{R}\) cuyas unidades cancelan las de\(|\chi_i(\textbf{S},\eta)|^2\).

Si multiplicamos esta velocidad a la que pasan las trayectorias\(\textbf{S}\),\(\eta\) por la probabilidad de\(P\) que ocurra un salto superficial e integremos sobre todo el espacio de la costura\(d\textbf{S}d\eta\), podemos expresar la velocidad a la que\(N\) las trayectorias sufrirán saltos

\[{\rm Rate}=\int NP|\chi_i(\textbf{S},\eta)|^2\frac{v_n}{\eta}d\textbf{S}d\eta = \int NP|\chi_i(\textbf{S},\eta)|^2v_n d\textbf{S}.\]

Si dividimos esta tasa por\(N\), el número de trayectorias, para producir la tasa promedio por trayectoria, y comparar esta expresión con la tasa que derivamos anteriormente

\[{\rm Rate}=\frac{2\pi}{\hbar}\int \chi_i^*(S,0)v_{i,f}^*v_{i,f}\frac{1}{|\nabla(V_f-V_i)|_S}\chi_i(S,0)dS\]

vemos que serían equivalentes si la probabilidad\(P\) de un salto superficial estuviera dada por

\[P=\frac{2\pi}{\hbar}v_{i,f}^*v_{i,f}\frac{1}{v_\eta|\nabla(V_f-V_i)|_S}.\]

La expresión anterior para la probabilidad de saltar de\(V_i(\textbf{R})\) a\(V_f(\textbf{R})\) se conoce como la fórmula Landau-Zener (LZ). La forma en que se utiliza en la mayoría de las aplicaciones es la siguiente:

1. Un conjunto de trayectorias clásicas con coordenadas iniciales y momentos seleccionados para representar una condición experimental se ejecutan en la superficie de energía potencial\(V_i(\textbf{R})\).
2. Siempre que cualquier trayectoria pasa muy cerca de una costura de intersección entre\(V_i(\textbf{R})\) y otra superficie\(V_f(\textbf{R})\),\(\textbf{R}\) se determina la geometría de costura\(\textbf{S}\) más cercana a y se evalúa el gradiente\(\nabla(V_f-V_i)\) de la diferencia de energía en\(\textbf{S}\). Además, se calcula el componente de la velocidad a lo largo de la dirección de este gradiente.
3. Los elementos de la matriz de acoplamiento electrónico entre los dos estados se evalúan en S, y la fórmula anterior se utiliza para estimar la probabilidad\(P\) de un salto superficial. En la mayoría de las aplicaciones de la teoría LZ, los estados electrónicos {\(\psi_{i,f}^0\)} en la región de una costura cruzada se toman como estados diabáticos porque entonces los elementos de la matriz de acoplamiento se pueden tomar de la división entre los dos estados adiabáticos que experimentan un cruce evitado cerca\(\textbf{S}\) en lugar de por evaluar elementos de la matriz de acoplamiento no adiabático\(\langle \psi_i|\dfrac{d\psi_f}{dR_b}\rangle \) entre estados de BO adiabáticos.

En resumen, la expresión LZ para la probabilidad de un salto de superficie debe verse como una versión aproximada del algoritmo proporcionado por el enfoque de salto de superficie de menos interruptores discutido anteriormente. Antes de cerrar esta Sección, es útil señalar cómo se aplica esta fórmula a dos casos distintos

1. Si, como se sugiere en la Figura 8.3 b, se prepara una molécula (por ejemplo, por absorción de fotones) en un estado electrónico excitado (la curva azul superior) que experimenta un cruce con un estado electrónico disociativo (la curva verde), se puede desear estimar la velocidad del proceso llamado predisociación en la que el excitado salta a la superficie disociativa y se desmorona. Esta tasa a menudo se calcula multiplicando la frecuencia\(\nu\) a la que la molécula excitada pasa a través del cruce de la curva por la estimación LZ de la probabilidad de salto superficial P:

\[{\rm Rate}=\nu P\]

con\(P\) computado como se discutió anteriormente y siendo\(\nu\) usualmente igual a la frecuencia vibracional del enlace cuyo estiramiento genera el cruce de la curva.

igure 8.3b Representación cualitativa de la predisociación que puede ocurrir desde una superficie excitada (azul) sobre una superficie disociativa (verde).

2. Alternativamente, uno puede estar interesado en determinar la probabilidad de que las especies de fragmentos (átomos en la Figura 8.3 b) colisionen sobre la curva verde y sufran una transición a la curva azul superior como resultado de esta colisión. Por ejemplo, la fluorescencia inmediata de esta curva azul superior podría ser la firma experimental que uno desea simular. En este caso, el resultado (es decir, la generación de la molécula en el estado electrónico de la curva azul superior) puede ocurrir de cualquiera de dos maneras:

a. El sistema choca sobre la curva verde y sufre un salto superficial en el cruce, terminando así en la superficie azul de la que rápidamente fluoresce; este proceso tiene una probabilidad\(P\) calculada usando la fórmula LZ.

b. El sistema choca sobre la curva verde y no salta a la curva azul en el cruce, sino que permanece en la curva verde (esto tiene probabilidad\(1-P\)) hasta que alcanza el punto de inflexión. Después de reflexionar sobre el punto de inflexión, el sistema (aún en la curva verde) salta a la curva azul (esto tiene probabilidad\(P\)) cuando vuelve a alcanzar el cruce tras lo cual ocurre la fluorescencia inmediata. La probabilidad general para este camino es\(P(1-P)\).

Entonces, el rendimiento total de fluorescencia estaría relacionado con la cantidad\(P + P(1-P)\). El punto de estos dos ejemplos es que la fórmula LZ da una estimación de la probabilidad de salto para un evento de cruce dado; todavía hay que pensar en cómo diversos eventos de cruce se relacionan con el experimento particular en cuestión.

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

• Integrated by Tomoyuki Hayashi (UC Davis)