6.4: Función de partición rotacional
- Page ID
- 71910
Asunción de Rotores Rígidos y Rotámeros
La separación de la función de partición rotacional de las funciones de partición de otros grados de libertad no solo requiere la consideración de los estados de espín nuclear, sino también la suposición de que el momento de inercia es el mismo para todos los estados rotacionales. Esto es generalmente cierto si la molécula se comporta como un rotor rígido. Para moléculas pequeñas que constan de solo unos pocos átomos, esto suele ser una buena aproximación. Las moléculas más grandes presentan rotaciones internas, donde un grupo de átomos gira con respecto al resto de la molécula. En general, las rotaciones internas son torsiones alrededor de uniones giratorias, que a menudo no son giratorias libremente. El potencial de torsión tiene varios mínimos y estos mínimos están separados por barreras de energía con alturas que son más grandes, pero no mucho mayores que\(k_\mathrm{B} T\). Si denotamos el número de mínimos potenciales para el enlace\(i^\mathrm{th}\) giratorio con\(n_{\mathrm{min},i}\), el número total de estados rotaméricos, los rotámeros cortos es
\[n_\mathrm{rot} = \prod_i n_{\mathrm{min},i} \ .\]
Cada rotámero tiene su propio momento de inercia y, de ahí, su propio conjunto de estados con respecto a la rotación total de la molécula. Debido a que las escalas de energía de las rotaciones internas y totales no están bien separadas y debido a que en moléculas más grandes algunos modos vibracionales también pueden tener energías en este rango, la función de partición no suele ser separable para moléculas grandes. En tales casos, el conocimiento de la termodinámica estadística se puede obtener mejor mediante simulaciones MD. A continuación, consideramos moléculas pequeñas que se puede suponer que se comportan como un rotor rígido. Primero consideramos las moléculas diatómicas, donde ciertamente se aplica en el nivel de precisión que buscamos aquí.
Los niveles de energía de un rotor rígido de una molécula diatómica son cuantificados por el número cuántico rotacional\(J\) y dados por
\[\epsilon_J = J(J+1) \frac{h^2}{8\pi^2 I} = h c B J (J+1) \ ,\]
donde
\[I = \mu r^2\]
es el momento de inercia con la masa reducida\(\mu\) y
\[B = \frac{h}{8 \pi^2 I c}\]
es la constante de rotación. Después de introducir la temperatura rotacional característica,
\[\Theta_\mathrm{rot} = \frac{h^2}{8 \pi^2 I k_\mathrm{B}} = \frac{h c B}{k_\mathrm{B}}\]
tenemos
\[\epsilon_J = J(J+1) k_\mathrm{B} \Theta_\mathrm{rot} \ .\]
Como ya se mencionó, cada nivel rotacional tiene una degeneración\(g_J = 2 J + 1\). Si todos los núcleos de las moléculas son distinguibles (magnéticamente no equivalentes), no hay correlación con los estados de espín nuclear. En ese caso tenemos
\[Z_\mathrm{rot} = \sum \left( 2 J + 1 \right) e^{-J(J+1)\Theta_\mathrm{rot}/T} \ . \label{eq:rot_sum}\]
Para temperaturas suficientemente altas y un momento de inercia suficientemente grande, la densidad de estados es suficientemente grande para reemplazar la suma por una integral,
\[Z_\mathrm{rot} \approx \int_0^\infty \left( 2 J + 1 \right) e^{-J(J+1)\Theta_\mathrm{rot}/T} \mathrm{d}J = \frac{T}{\Theta_\mathrm{rot}} \ . \label{eq:continuum}\]
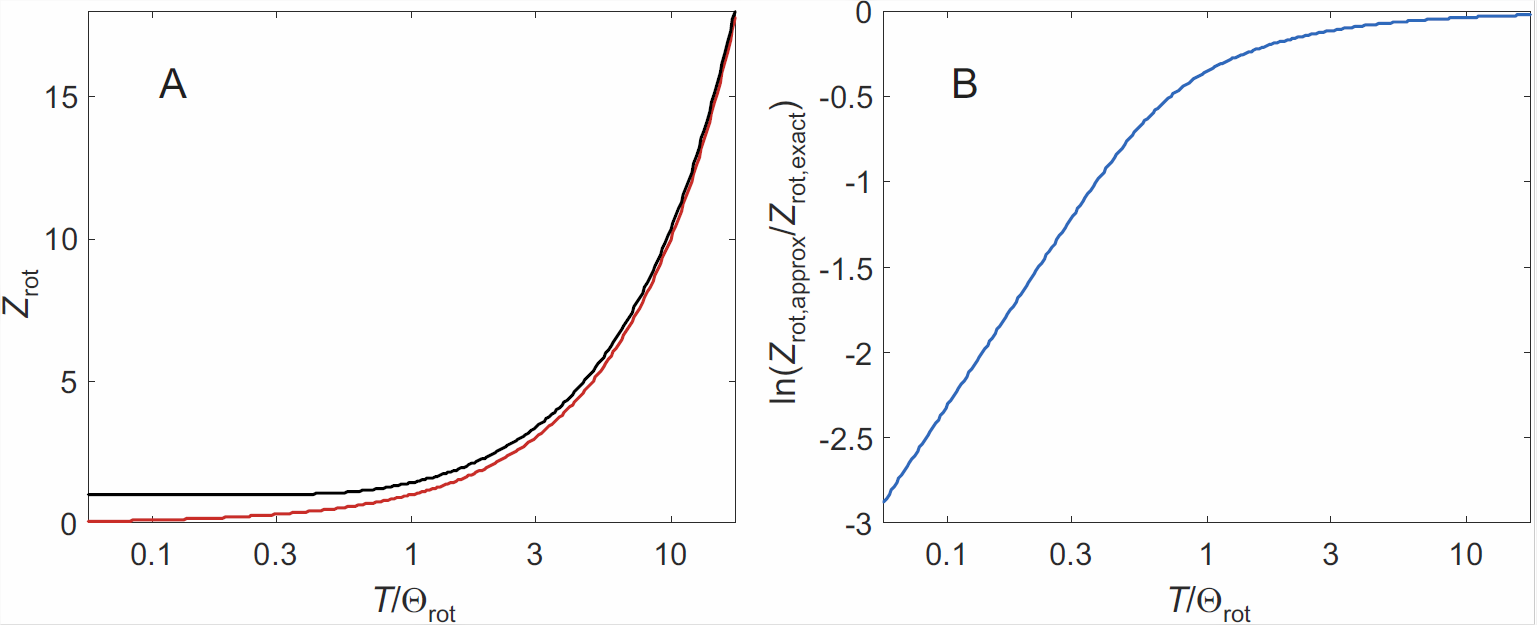
Las desviaciones entre las funciones de partición calculadas por la ecuación\ ref {eq:rot_sum}) y la ecuación\ ref {eq:continuum}) se visualizan en la Figura\(\PageIndex{1}\). Como dependen las funciones de estado\(\ln Z\), la aproximación continua es buena para\(T/\Theta_\mathrm{rot} \gg 1\), lo que se aplica a todos los gases, excepto a bajas temperaturas para aquellos que contienen hidrógeno. A temperatura ambiente se puede utilizar en general, a excepción de una corrección adicional que necesitamos hacer por consideraciones de simetría.
Estados accesibles y simetría
Incluso si todos los núcleos son magnéticamente inequivalentes y, por lo tanto, distinguibles, los estados rotacionales pueden no serlo. Para las moléculas diatómicas heteronucleares lo son, pero para las moléculas diatómicas homonucleares, no lo son. Para ver esto, consideramos una molécula lineal simétrica que gira 180\(^\circ\) alrededor de un eje perpendicular al eje del enlace y centrada en el medio del enlace. Esta rotación produce una configuración que es indistinguible de la configuración original. Es decir, la función de onda nuclear es simétrica con respecto a esta rotación. Para una molécula diatómica homonuclear, la mitad de los estados rotacionales son simétricos y la mitad son antisimétricos. Para núcleos que son bosones, como\(\ce{^{16}O}\) en el dioxígeno, solo se permiten los primeros estados, para los núcleos que son fermiones, solo se permiten los últimos. De ahí que necesitamos dividir la función de partición, que cuenta estados accesibles, por dos. En este ejemplo, hemos elegido deliberadamente un caso con un solo estado de giro nuclear. Si existen estados de espín nuclear con simetría diferente, todos los estados rotacionales son accesibles, pero correlacionados con los estados de espín nuclear, como hemos visto antes para el dihidrógeno. A continuación consideramos la situación con un solo estado de giro nuclear o para un estado de giro nuclear fijo.
| Grupo | \(\sigma\) | Grupo | \(\sigma\) | Grupo | \(\sigma\) | Grupo | \(\sigma\) |
|---|---|---|---|---|---|---|---|
| \(C_1\),\(C_i\),\(C_s\),\(C_{\infty v}\) | \ (\ sigma\) ">1 | \(D_{\infty h}\) | \ (\ sigma\) ">2 | \(T\),\(T_d\) | \ (\ sigma\) ">12 | \(O_h\) | \ (\ sigma\) ">24 |
| \(C_n\),\(C_{nv}\),\(C_{nh}\) | \ (\ sigma\) ">\(n\) | \(D_n\),\(D_{nh}\),\(D_{nd}\) | \ (\ sigma\) ">\(2 n\) | \(S_n\) | \ (\ sigma\) ">\(n/2\) | \(I_h\) | \ (\ sigma\) ">60 |
Aunque todavía no discutimos otras complicaciones para las moléculas multiatómicas, generalizamos este concepto de estados accesibles a la simetría introduciendo un número de simetría\(\sigma\). En general,\(\sigma\) es el número de orientaciones distintas de una molécula rígida que se distinguen únicamente por el intercambio de átomos idénticos. Para una\(_3\) molécula NH, la rotación alrededor del\(C_3\) eje en 120\(^\circ\) genera una orientación de este tipo con respecto a la otra. No existe otro eje de rotación. De ahí,\(\sigma = 3\) para NH\(_3\). En general, el número de simetría se puede obtener a partir del grupo puntual de la molécula, como se muestra en la Tabla\(\PageIndex{1}\).
Con el número de simetría, la aproximación de continuum (Ecuación\ ref {eq:continuum} se convierte
\[Z_\mathrm{rot} = \frac{T}{\sigma \Theta_\mathrm{rot}} \ , \label{eq:Z_rot}\]
donde todavía asumimos que la simetría es suficientemente alta para asignar una única temperatura característica.
Además, encontramos
\[\ln Z_\mathrm{rot} = \ln T + \ln \frac{1}{\sigma \Theta_\mathrm{rot}} \ , \label{eq:ln_Z_rot}\]
y con esto
\[\begin{align} U_\mathrm{rot} = N_\mathrm{Av} k_\mathrm{B} T^2 \left( \frac{\partial \ln Z_\mathrm{rot}}{\partial T} \right)_V \label{eq:u_rot0} \\ = R T^2 \frac{\partial}{\partial T} \ln T \label{eq:u_rot1} \\ = R T \ \textrm{(linear)} \ .\end{align}\]
Al pasar de la Ecuación\ ref {eq:u_rot0} a\ ref {eq:u_rot1} podríamos dejar caer el segundo término en el lado derecho de la Ecuación\ ref {eq:Ln_z_rot}, ya que este término no depende de la temperatura. Este es un principio general: Los factores constantes en la función de partición no contribuyen a la energía interna. El resultado puede generalizarse a moléculas lineales multiatómicas que también tienen dos grados de libertad rotacional. Este resultado se espera del teorema de equipartición, ya que cada grado de libertad debe aportar un término\(k_\mathrm{B} T/2\) a lo molecular o un término\(R T/2\) a la energía interna molar. Sin embargo, si nos abstenemos de la aproximación de continuum en la Ecuación\ ref {eq:continuum}) y evaluamos numéricamente la Ecuación\ ref {eq:rot_sum}) en su lugar, encontramos una menor contribución para temperaturas inferiores o comparables a\(\Theta_\mathrm{rot}\). Este es también un principio general: Las contribuciones de los modos a la energía interna y, por inferencia, a la capacidad calorífica, se realizan plenamente sólo a temperaturas muy superiores a su temperatura característica y son despreciables a temperaturas mucho más bajas que su temperatura característica. 20
Para la contribución de rotación a la capacidad calorífica molar a volumen constante de una molécula lineal obtenemos
\[C_{\mathrm{rot},V} = \frac{\partial}{\partial T} U_\mathrm{rot} = R \ .\]
Una molécula multiatómica no lineal tiene, en general, tres momentos de inercia rotacionales independientes correspondientes a tres direcciones ortogonales por pares\(a, b, c\). Con
\[\Theta_{\mathrm{rot},\alpha} = \frac{h^2}{8 \pi^2 I_\alpha k_\mathrm{B}} \ \left( \alpha = a \ , b \ , c \right)\]
uno encuentra para la función de partición
\[Z_\mathrm{rot} = \frac{\sqrt{\pi}}{\sigma} \left( \frac{T^3}{\Theta_{\mathrm{rot},a} \Theta_{\mathrm{rot},b} \Theta_{\mathrm{rot},c}} \right)^{1/2} \ .\]
Para las moléculas esférico-superiores, los tres momentos de inercia son iguales\(I_a = I_b = I_c\), y por lo tanto las tres temperaturas características son iguales. Para moléculas simétricas superiores,\(I_a = I_b \neq I_c\).
Las ecuaciones generales para\(U_\mathrm{rot}\) y\(C_{\mathrm{rot},V}\) a temperatura suficientemente alta\(T \gg \Theta_\mathrm{rot}\) son
\[\begin{align} U_\mathrm{rot} & = \frac{d}{2} R T \\ C_{\mathrm{rot},V} & = \frac{d}{2} R \ ,\end{align}\]
donde\(d = 1\) para una rotación interna libre (por ejemplo, alrededor de un enlace\(\equiv\) C C),\(d=2\) para moléculas lineales y\(d=3\) no lineales. Observamos que la contribución de una rotación interna libre necesita ser sumada a la contribución de la rotación total de la molécula.
Las expresiones para las contribuciones rotacionales a la entropía molar son un poco largas y no proporcionan una visión física adicional. Se pueden derivar fácilmente de las expresiones apropiadas para la función de partición rotacional y la energía interna usando la ecuación\ ref {eq:s_from_z}). Observamos, sin embargo, que la contribución del\(u/T\) término en la expresión de entropía es\(d R/2\) y la contribución de\(\ln Z\) es positiva. Por lo tanto, a temperaturas donde la aproximación continua es válida, la contribución rotacional a la entropía es mayor que\(d R/2\).

