9.3: El diferencial total
- Page ID
- 75291
En el Capítulo 8 aprendimos que las derivadas parciales indican cómo cambia la variable dependiente con una variable independiente en particular manteniendo las otras fijas. En el contexto de una ecuación de estado\(P=P(T,V,n)\), la derivada parcial de\(P\) con respecto a\(V\) a constante\(T\) y\(n\) es:
\[\left (\dfrac{\partial P}{\partial V} \right )_{T,n} \nonumber\]
y representa físicamente cómo varía la presión a medida que cambiamos el volumen a temperatura constante y constante\(n\).
La derivada parcial de\(P\) con respecto a\(T\) a constante\(V\) y\(n\) es:
\[\left (\dfrac{\partial P}{\partial T} \right )_{V,n} \nonumber\]
y representa físicamente cómo varía la presión a medida que cambiamos la temperatura a volumen constante y constante\(n\).
¿Qué sucede con la variable dependiente (en este caso\(P\)) si cambiamos dos o más variables independientes simultáneamente? Para un cambio infinitesimal en volumen y temperatura, podemos escribir el cambio en la presión como:
\[\label{eq:differentials1} dP=\left (\dfrac{\partial P}{\partial V} \right )_{T,n} dV+\left (\dfrac{\partial P}{\partial T} \right )_{V,n} dT\]
Ecuación\ ref {eq:diferenciales1} se llama el diferencial total de P, y simplemente establece que el cambio en\(P\) es la suma de las contribuciones individuales debido\(V\) al cambio en constante\(T\) y el cambio\(T\) en constante\(V\). Esta ecuación es cierta para los cambios infinitesimales. Si los cambios no son infinitesimales integraremos esta expresión para calcular el cambio en\(P\). [diferenciales_posiciones1]
Consideremos ahora el volumen de un fluido, que es función de la presión, la temperatura y el número de moles:\(V=V(n,T,P)\). El diferencial total de\(V\), por definición, es:
\[\label{eq:differentials3} dV=\left (\frac{\partial V}{\partial T} \right )_{P,n} dT+\left (\frac{\partial V}{\partial P} \right )_{T,n} dP+\left (\frac{\partial V}{\partial n} \right )_{T,V} dn\]
Si queremos calcular el cambio de volumen en un fluido sobre pequeños cambios en\(P, T\) y\(n\), podríamos usar:
\[\label{eq:differentials3b} \Delta V\approx \left (\frac{\partial V}{\partial T} \right )_{P,n} \Delta T+\left (\frac{\partial V}{\partial P} \right )_{T,n} \Delta P+\left (\frac{\partial V}{\partial n} \right )_{T,V} \Delta n\]
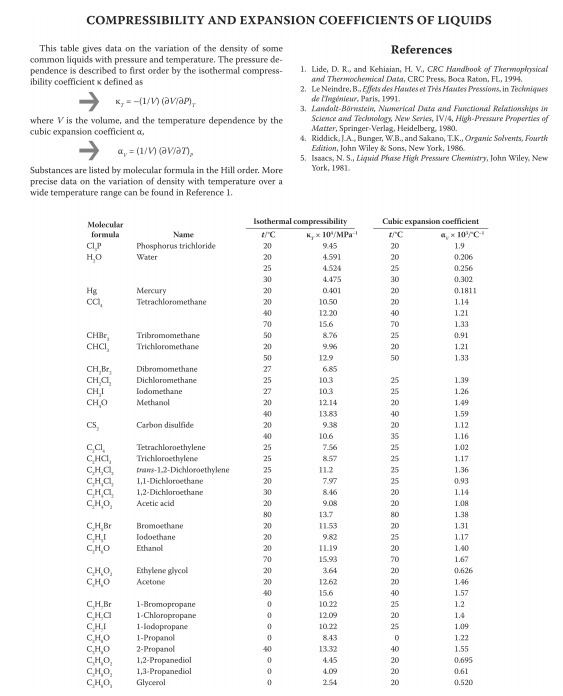
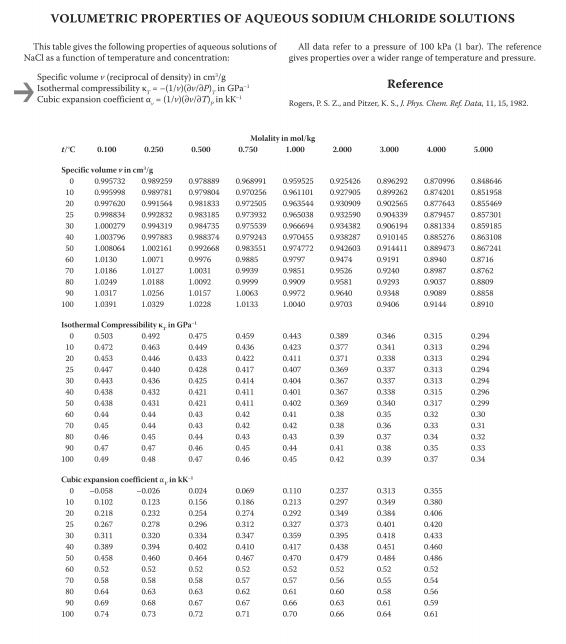
Por supuesto, si conocemos la función\(V=V(n,T,P)\), también podríamos calcular\(\Delta V\) como\(V_f-F_i\), donde se calculan los volúmenes final e inicial utilizando los valores final e inicial de\(P, T\) y\(n\). Esto parece fácil, entonces ¿por qué tenemos que molestarnos con la Ecuación\ ref {eq:differentials3b}? La razón es que a veces podemos medir las derivadas parciales experimentalmente, pero no tenemos una ecuación del tipo\(V=V(n,T,P)\) a usar. Por ejemplo, las siguientes cantidades son accesibles experimentalmente y tabuladas para diferentes fluidos y materiales (Fig. [fig:diff_tables]):
- \(\alpha=\frac{1}{V}\left(\frac{\partial V}{\partial T} \right )_{P,n}\)(coeficiente de expansión térmica)
- \(\kappa=-\frac{1}{V}\left(\frac{\partial V}{\partial P} \right )_{V,n}\)(compresibilidad isotérmica) [diferenciales:compresibilidad]
- \(V_m=\left(\frac{\partial V}{\partial n} \right )_{P,T}\)(volumen molar)
Usando estas definiciones, la ecuación\ ref {eq:diferenciales3} se convierte en:
\[\label{eq:differentials4} dV=\alpha V dT-\kappa VdP+V_m dn\]
Puede encontrar tablas con valores determinados experimentalmente de\(\alpha\) y\(\kappa\) bajo diferentes condiciones, que puede utilizar para calcular los cambios en\(V\). Nuevamente, como veremos más adelante en este capítulo, esta ecuación tendrá que integrarse si los cambios no son pequeños. En cualquier caso, el punto es que puede tener acceso a información sobre las derivadas de la función, pero no a la función en sí (en este caso\(V\) en función de\(T, P, n\)).
En general, para una función\(u=u(x_1, x_2...x_n)\), definimos el diferencial total de\(u\) como:
\[\label{eq:total_differential} du=\left (\frac{\partial u}{\partial x_1} \right )_{x_2...x_n} dx_1+\left (\frac{\partial u}{\partial x_2} \right )_{x_1, x_3...x_n} dx_2+...+\left (\frac{\partial u}{\partial x_n} \right )_{x_1...x_{n-1}} dx_n\]
Ejemplo\(\PageIndex{1}\)
Calcular el diferencial total de la función\(z=3x^3+3yx^2+xy^2\).
Solución
Por definición, el diferencial total es:
\[dz=\left (\frac{\partial z}{\partial x} \right )_{y} dx+\left (\frac{\partial z}{\partial y} \right )_{x} dy \nonumber\]
Para la función dada en el problema,
\[\left (\frac{\partial z}{\partial x} \right )_{y}=9x^2+6xy+y^2 \nonumber\]
y
\[\left (\frac{\partial z}{\partial y} \right )_{x}=3x^2+2xy \nonumber\]
y por lo tanto,
\[\displaystyle{\color{Maroon}dz=(9x^2+6xy+y^2)dx+(3x^2+2xy)dy} \nonumber\]
¿Quieres ver más ejemplos?
- Ejemplo 1: http://www.youtube.com/watch?v=z0TxZ0EHzIg Observe que ella lo llama 'el diferencial', pero prefiero 'el diferencial total'.

