9.2: Funciones de dos variables independientes
- Page ID
- 75275
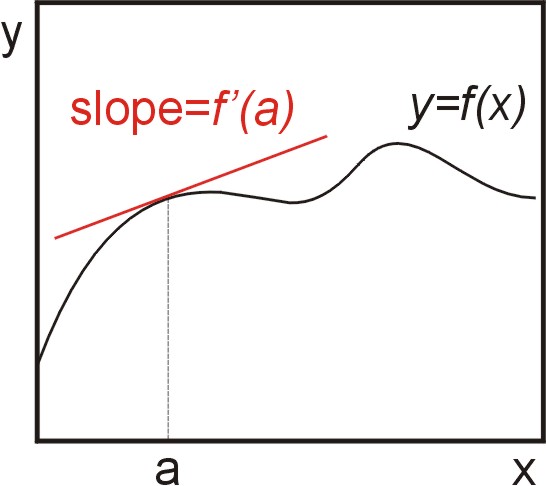
Una función (real) de una variable,\(y = f(x)\), define una curva en el plano. La primera derivada de una función de una variable se puede interpretar gráficamente como la pendiente de una línea tangente, y dinámicamente como la tasa de cambio de la función con respecto a la variable Figura\(\PageIndex{1}\).
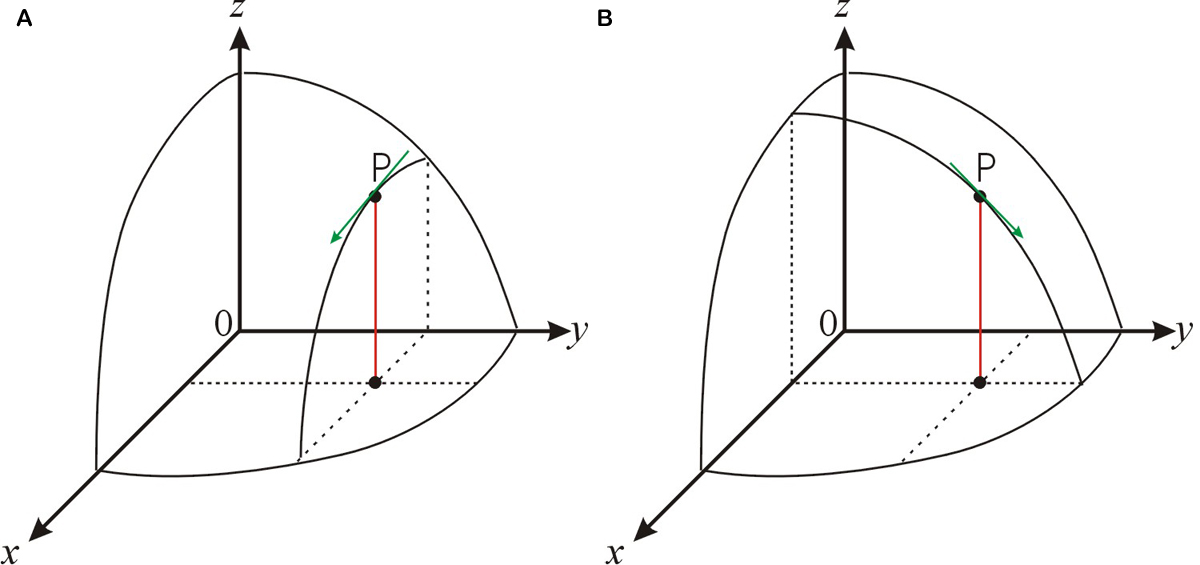
Una función de dos variables independientes,\(z=f (x,y)\), define una superficie en el espacio tridimensional. Para una función de dos o más variables, hay tantas primeras derivadas independientes como variables independientes. Por ejemplo, podemos diferenciar la función\(z=f (x,y)\) con respecto a\(x\) mantener\(y\) constante. Esta derivada representa la pendiente de la línea tangente mostrada en la Figura\(\PageIndex{2} \text{A}\). También podemos tomar la derivada con respecto a\(y\) mantener\(x\) constante, como se muestra en la Figura\(\PageIndex{2} \text{B}\).
Por ejemplo, consideremos la función\(z=3x^2-y^2+2xy\). Podemos tomar la derivada de esta función con respecto al\(x\) tratamiento\(y\) como una constante. El resultado es\(6x+2y\). Esta es la derivada parcial de la función con respecto a\(x\), y está escrito:
\[\left (\frac{\partial z}{\partial x} \right )_y=6x+2y \nonumber\]
donde los subíndices pequeños indican qué variables se mantienen constantes. Análogamente, el derivado parcial de\(z\) con respecto a\(y\) es:
\[\left (\frac{\partial z}{\partial y} \right )_x=2x-2y \nonumber\]
Podemos extender estas ideas a funciones de más de dos variables. Por ejemplo, considere la función\(f(x,y,z)=x^2y/z\). Podemos diferenciar la función con respecto a\(x\) mantener\(y\) y\(z\) constante para obtener:
\[\left (\frac{\partial f}{\partial x} \right )_{y,z}=2x\frac{y}{z} \nonumber\]
También podemos diferenciar la función con respecto a\(z\) mantener\(x\) y\(y\) constante:
\[\left (\frac{\partial f}{\partial z} \right )_{x,y}=-x^2y/z^2 \nonumber\]
y diferenciar la función con respecto a\(y\) mantener\(x\) y\(z\) constante:
\[\left (\frac{\partial f}{\partial y} \right )_{x,z}=\frac{x^2}{z} \nonumber\]
Las funciones de dos o más variables pueden diferenciarse parcialmente más de una vez con respecto a cualquiera de las variables mientras se mantiene la otra constante para producir segundas y mayores derivadas. Por ejemplo, la función se\(z=3x^2-y^2+2xy\) puede diferenciar con respecto a\(x\) dos veces para obtener:
\[\left ( \frac{\partial }{\partial x}\left ( \frac{\partial z}{\partial x} \right )_{y} \right )_{y}=\left ( \frac{\partial ^2z}{\partial x^2} \right )_{y}=6 \nonumber\]
También podemos diferenciar con respecto a\(x\) primero y\(y\) segundo:
\[\left ( \frac{\partial }{\partial y}\left ( \frac{\partial f}{\partial x} \right )_{y} \right )_{x}=\left ( \frac{\partial ^2f}{\partial y \partial x} \right )=2 \nonumber\]
Consulta los videos a continuación si estás aprendiendo esto por primera vez, o si sientes que necesitas refrescar el concepto de derivados parciales.
- Derivadas parciales: http://patrickjmt.com/derivatives-finding-partial-derivatives (¡no te confundas por la notación diferente!)
- Derivadas parciales: http://www.youtube.com/watch?v=vxJR5graUfI
- Derivadas parciales de orden superior: http://www.youtube.com/watch?v=3itjTS2Y9oE
Si una función de dos o más variables y sus derivadas son de valor único y continuas, una propiedad normalmente atribuida a variables físicas, entonces las segundas derivadas parciales mixtas son iguales (reciprocidad de Euler):
\[\label{c2v:euler reciprocity} \left ( \frac{\partial ^2f}{\partial x \partial y} \right )=\left ( \frac{\partial ^2f}{\partial y \partial x} \right )\]
Por ejemplo, para\(z=3x^2-y^2+2xy\):
\[\left ( \frac{\partial ^2f}{\partial y \partial x} \right )=\left ( \frac{\partial }{\partial y}\left ( \frac{\partial f}{\partial x} \right )_{y} \right )_{x}=\left ( \frac{\partial }{\partial y}\left ( 6x+2y\right ) \right )_{x}=2 \nonumber\]
\[\left ( \frac{\partial ^2f}{\partial x \partial y} \right )=\left ( \frac{\partial }{\partial x}\left ( \frac{\partial f}{\partial y} \right )_{x} \right )_{y}=\left ( \frac{\partial }{\partial x}\left ( -2y+2x\right ) \right )_{y}=2 \nonumber\]
Otra propiedad útil de las derivadas parciales es la llamada identidad recíproca, que se mantiene cuando las mismas variables se mantienen constantes en las dos derivadas:
\[\label{c2v:inverse} \left ( \frac{\partial y}{\partial x} \right )=\frac{1}{\left ( \frac{\partial x}{\partial y} \right )}\]
Por ejemplo, para\(z=x^2y\):
\[\left ( \frac{\partial z}{\partial x} \right )_y=\left ( \frac{\partial }{\partial x} x^2y\right )_y=2xy \nonumber\]
\[\left ( \frac{\partial x}{\partial z} \right )_y=\left ( \frac{\partial }{\partial z} \sqrt{z/y} \right )_y=\frac{1}{2y} (z/y)^{-1/2}=\frac{1}{2xy}=\frac{1}{\left ( \frac{\partial z}{\partial x} \right )}_y \nonumber\]
Por último, mencionemos la regla del ciclo. Para una función\(z(x,y)\):
\[\label{c2v:cycle} \left ( \frac{\partial y}{\partial x} \right )_z\left ( \frac{\partial x}{\partial z} \right )_y\left ( \frac{\partial z}{\partial y} \right )_x=-1\]
Podemos construir otras versiones de la siguiente manera:
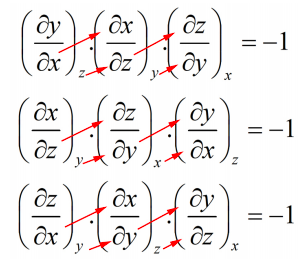
Por ejemplo, para\(z=x^2y\):
\[\left ( \frac{\partial y}{\partial x} \right )_z=\left ( \frac{\partial }{\partial x} (z/x^2)\right )_z=-2z/x^3 \nonumber\]
\[\left ( \frac{\partial x}{\partial z} \right )_y=\left ( \frac{\partial }{\partial z} \sqrt{z/y}\right )_y=\frac{1}{2y} (z/y)^{-1/2} \nonumber\]
\[\left ( \frac{\partial z}{\partial y} \right )_x=\left ( \frac{\partial }{\partial y} x^2y\right )_x=x^2 \nonumber\]
\[\left ( \frac{\partial y}{\partial x} \right )_z\left ( \frac{\partial x}{\partial z} \right )_y\left ( \frac{\partial z}{\partial y} \right )_x=-\frac{2z}{x^3}\frac{1}{2y} \left(\frac{y}{z}\right)^{1/2}x^2=-\left(\frac{z}{y}\right)^{1/2}\frac{1}{x}=-\left(\frac{x^2y}{y}\right)^{1/2}\frac{1}{x}=-1 \nonumber\]
Antes de discutir más sobre derivados parciales, introduzcamos algunos conceptos fisicoquímicos para poner nuestra discusión en contexto.

