12: Equilibrios de solubilidad
- Page ID
- 70633
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Asegúrese de comprender a fondo las siguientes ideas esenciales:
- Discutir los roles de la energía reticular y de hidratación en la determinación de la solubilidad de una sal en agua.
- Explicar qué es un esquema de separación de análisis cualitativo y cómo funciona.
- Escribir la expresión del producto de solubilidad para una sal, dada su fórmula.
- Explicar la distinción entre un producto iónico y un producto de solubilidad.
- Dada la fórmula de una sal y su valor K s, calcular la solubilidad molar.
- Explicar el principio de Le Chatelier conduce al efecto de iones comunes.
- Explica por qué un ácido fuerte como el HCl disolverá una sal escasamente soluble de un ácido débil, pero no una sal de un ácido fuerte.
- Describir qué sucede (y por qué) cuando se agrega lentamente amoníaco acuoso a una solución de nitrato de plata
La disolución de una sal en agua es un proceso químico que se rige por las mismas leyes de equilibrio químico que se aplican a cualquier otra reacción. Hay, sin embargo, una serie de aspectos especiales de estos equilibrios que los diferencian un poco de los más generales que se tratan en el conjunto de lecciones dedicado específicamente al equilibrio químico. Estos incluyen temas como el efecto iónico común, la influencia del pH en la solubilidad, la sobresaturación y algunas características especiales de los sistemas de solubilidad particularmente importantes.
Solubilidad: la disolución de sales en agua
Deja caer un poco de sal de mesa ordinaria en un vaso de agua, y mírala “desaparecer”. Nos referimos a esto como disolución, y lo explicamos como un proceso en el que las unidades de sodio y cloro se separan de la superficie cristalina, quedan rodeadas por moléculas de H 2 O y se convierten en iones hidratados.
\[NaCl_{(s)} \rightarrow Na^+_{(aq)}+ Cl^–_{(aq)} \]
La designación (aq) significa “acuoso” y proviene de aqua, la palabra latina para agua. Se utiliza siempre que queremos enfatizar que los iones están hidratados —que las moléculas de H 2 O están unidas a ellos.
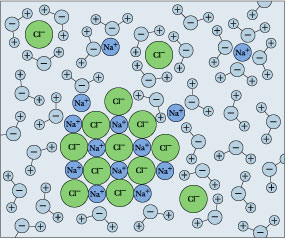
Recuerde que el equilibrio de solubilidad y los cálculos que se relacionan con él solo son significativos cuando ambos lados (sólidos e iones disueltos) están presentes simultáneamente. Pero si sigues agregando sal, llegará un punto en el que ya no parece disolverse. Si esta condición persiste, decimos que la sal ha alcanzado su límite de solubilidad, y la solución está saturada en NaCl. La situación se describe ahora por
\[NaCl_{(s)} \rightleftharpoons Na^+_{(aq)}+ Cl^–_{(aq)}\]
en el que el sólido y sus iones están en equilibrio.
Las soluciones salinas que han alcanzado o excedido sus límites de solubilidad (generalmente 36-39 g por 100 mL de agua) son responsables de características destacadas de la geoquímica terrestre. Normalmente se forman cuando el NaCl lixivia de suelos hacia aguas que desembocan en lagos salados en regiones áridas que no tienen salidas naturales; la posterior evaporación de estas salmueras fuerza el equilibrio anterior hacia la izquierda, formando depósitos naturales de sal. Estas a menudo se mezclan con otras sales, pero en algunos casos son NaCl casi puro. Muchas partes del mundo contienen depósitos enterrados de NaCl (conocidos como halita) que se formaron a partir de la evaporación de mares antiguos, y que ahora se extraen.
Las solubilidades se expresan fundamentalmente en unidades molares (mol L —1 de solución) o molal (mol kg —1 de agua). Pero para su uso práctico en la preparación de soluciones madre, los manuales de química suelen expresar solubilidades en términos de gramos por 100 ml de agua a una temperatura determinada, señalando frecuentemente esta última en un superíndice. Así 6.9 20 significa 6.9 g de soluto se disolverán en 100 mL de agua a 20°C. Cuando faltan datos cuantitativos, se utilizan las denominaciones “soluble”, “insoluble”, “ligeramente soluble” y “altamente soluble”. No existe un estándar acordado para estas clasificaciones, pero una guía útil podría ser la que se muestra a continuación.
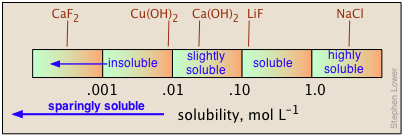
Las solubilidades de las sales en el agua abarcan un rango notablemente grande de valores, desde casi completamente insolubles hasta altamente solubles. Además, no existe una manera sencilla de predecir estos valores, ni siquiera de explicar las tendencias que se observan para las solubilidades de diferentes aniones dentro de un grupo dado de la tabla periódica.

En última instancia, la fuerza impulsora para la disolución (y para todos los procesos químicos) está determinada por el cambio de energía libre de Gibbs. Pero debido a que muchos cursos cubren la solubilidad antes de introducir la energía libre, no vamos a perseguir esto aquí. La disolución de una sal se entiende conceptualmente como una secuencia de los dos procesos descritos anteriormente:
- ruptura de la red iónica del sólido,
- seguido de la unión de moléculas de agua a los iones liberados.
El primer paso consume una gran cantidad de energía, algo que por sí mismo desalentaría fuertemente la solubilidad. Pero el segundo paso libera una gran cantidad de energía y así tiene el efecto contrario. Así, el cambio neto de energía depende de la suma de dos grandes términos de energía (a menudo acercándose a 1000 kJ/mol) que tienen signos opuestos. Cada uno de estos términos estará influenciado en cierta medida por el tamaño, la carga y la polarizabilidad de los iones particulares involucrados, y por la estructura reticular del sólido. Este gran número de variables hace imposible predecir la solubilidad de una sal dada. Sin embargo, hay algunas tendencias claras de cómo las solubilidades de una serie de sales de un anión dado (como hidróxidos, sulfatos, etc.) cambian con un grupo de tabla periódica. Y por supuesto, hay una serie de reglas generales de solubilidad —por ejemplo, que todos los nitratos son solubles, mientras que la mayoría de los sulfuros son insolubles.
Solubilidad y temperatura
La solubilidad suele aumentar con la temperatura, pero no siempre. Esto es muy evidente a partir de la solubilidad-vs. -gráficas de temperatura que se muestran aquí. (Algunas de las parcelas están coloreadas de manera diferente para que sea más fácil distinguirlas donde se agrupan). La dependencia de la temperatura de cualquier proceso depende de su cambio de entropía, es decir, del grado en que la energía cinética térmica puede extenderse por todo el sistema. Cuando un sólido se disuelve, sus moléculas componentes o iones se difunden en el volumen mucho mayor de la solución, llevando su energía térmica junto con ellos. Por lo que normalmente esperaríamos que la entropía aumentara —algo que hace que cualquier proceso se lleve a cabo en mayor medida a una temperatura más alta.
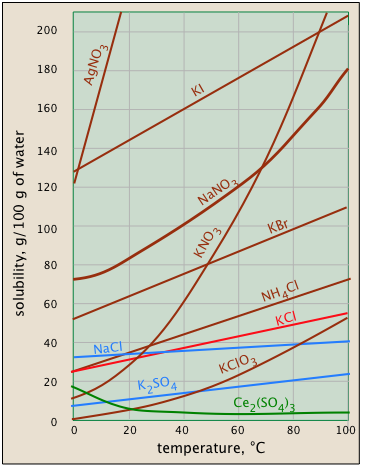
Entonces, ¿por qué la solubilidad del sulfato de cerio (parcela verde) disminuye con la temperatura? La dispersión de los iones Ce 3 + y SO 4 2— todavía se asocia con un aumento de entropía, pero en este caso la entropía del agua disminuye aún más debido al orden de las moléculas H 2 O que se unen al Ce 3 + iones a medida que se hidratan. Es difícil predecir estos efectos, o explicar por qué ocurren en casos individuales, pero sí suceden.
La importancia de los sólidos escasamente solubles
Todos los sólidos que se disocian en iones exhiben cierto límite a sus solubilidades, pero aquellos cuyas soluciones saturadas superan aproximadamente 0.01 mol L —1 no pueden ser tratados por constantes de equilibrio simples debido a la formación de pares iónicos que complica enormemente su comportamiento. Por esta razón, la mayor parte de lo que sigue en esta lección se limita a las sales que entran en la categoría de “escasamente solubles”. La importancia de los sólidos escasamente solubles surge del hecho de que la formación de dicho producto puede eliminar efectivamente los iones correspondientes de la solución, impulsando así la reacción hacia la derecha. Consideremos, por ejemplo, lo que sucede cuando mezclamos soluciones de nitrato de estroncio y cloruro de potasio en una relación molar 1:2. Aunque podríamos representar este proceso por
\[Sr(NO_3)_{2(aq)}+ 2 KCl_{(aq)}→ SrCl_{(aq)}+ 2 KNO_{3(aq)} \label{1}\]
la ecuación iónica neta
\[Sr^{2+} + 2 NO_3^– + 2 K^+ + 2 Cl^– → Sr^{2+} + 2 NO_3^– + 2 K^+ + 2 Cl^–\]
indica que ¡no se ha producido ningún cambio neto en absoluto! Por supuesto, si la solución se evaporara luego a sequedad, terminaríamos con una mezcla de las cuatro sales que se muestran en la Ecuación\(\ref{1}\), así que en este caso podríamos decir que la reacción es semicompleta. Contraste esto con lo que sucede si combinamos soluciones equimolares de cloruro de bario y sulfato de sodio:
\[BaCl_{2(aq)}+ Na_2SO_{4(aq)}→ 2 NaCl_{(aq)}+ BaSO_{4(s)} \label{2}\]
cuya ecuación iónica neta es
\[Ba^{2+} + \cancel{ 2 Cl^–} + \cancel{2 Na^+} + SO_4^{2–} → \cancel{2 Na^+} + \cancel{2 Cl^–} + BaSO_{4(s)}\]
que después de cancelar términos similares en ambos lados, se convierte simplemente
\[Ba^{2+} + SO_4^{2– }→ BaSO_{4(s)} \label{3}\]
Debido a que la formación de sólidos escasamente solubles es “completa” (es decir, equilibrios como el mostrado anteriormente para el sulfato de bario se encuentran hasta ahora a la derecha), prácticamente todos uno o ambos iones contribuyentes se eliminan esencialmente de la solución. Se dice que tales reacciones son cuantitativas, y son especialmente importantes en la química analítica:
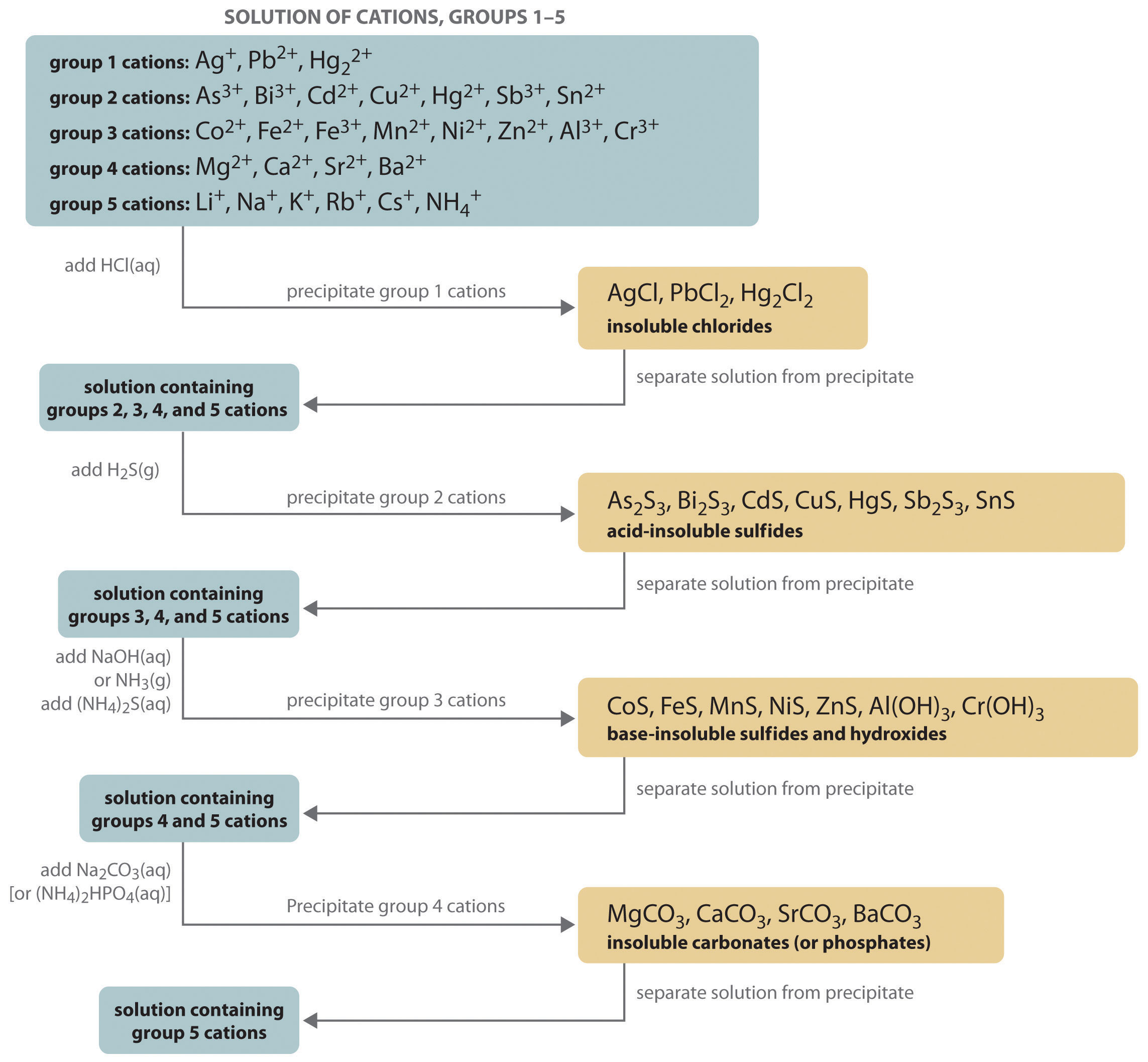
- Análisis cualitativo: Esto se refiere más comúnmente a un esquema procesal, ampliamente encontrado en cursos de laboratorio de primer año, en el que una mezcla de cationes (generalmente en forma de sus sales de nitrato disueltas) se separa e identifica sistemáticamente en base a las solubilidades de sus diversas sales aniónicas tales como cloruros, carbonatos, sulfatos y sulfuros. Aunque esta forma de análisis cualitativo ya no es empleada por los químicos modernos (las técnicas instrumentales como la espectroscopía de absorción atómica son mucho más rápidas e integrales), aún se valora como una herramienta educativa para familiarizar a los estudiantes con algunas de las principales clases de inorgánica sales, y para desarrollar habilidades básicas relacionadas con la observación, organización e interpretación de resultados en el laboratorio.
- Análisis gravimétrico cuantitativo: En esta forma clásica de análisis químico, se prepara una sal insoluble de un catión precipitándolo mediante la adición de un anión adecuado. Luego, el precipitado se recoge, se seca y se pesa (“gravimetría”) para determinar la concentración del catión en la muestra. Por ejemplo, un procedimiento gravimétrico para determinar la cantidad de bario en una muestra podría implicar precipitar el metal como el sulfato de acuerdo con la Ecuación\(\ref{3}\) anterior, utilizando un exceso de ion sulfato para asegurar la eliminación completa del bario. Este método de análisis cuantitativo adquirió una importancia extrema en la segunda mitad del siglo XIX, momento en el que se disponía de pesos atómicos razonablemente precisos y se habían desarrollado balanzas analíticas sensibles. No fue hasta la década de 1960 que quedó suplantada en gran medida por técnicas instrumentales que eran mucho más rápidas y precisas. El análisis gravimétrico todavía se incluye generalmente como parte de la instrucción de laboratorio más avanzada, en gran parte como un medio para desarrollar una técnica de laboratorio cuidadosa.
Productos de Solubilidad y Equilibrios
Algunas sales y compuestos similares (como algunos hidróxidos metálicos) se disocian por completo cuando se disuelven, pero el grado en que se disuelven es tan limitado que las soluciones resultantes muestran solo conductividades muy débiles. En estas sales, que de otra manera actúan como electrolitos fuertes, podemos tratar el proceso de disolución-disociación como un verdadero equilibrio. Si bien esto parece casi trivial ahora, este descubrimiento, realizado en 1900 por Walther Nernst quien aplicó la Ley de Acción de Masas al esquema de disociación de Arrhenius, es considerado uno de los principales pasos en el desarrollo de nuestra comprensión de las soluciones iónicas.
Usando el cromato de plata como ejemplo, expresamos su disolución en agua como
\[Ag_2CrO_{4(s)} \rightarrow 2 Ag^+_{(aq)}+ CrO^{2–}_{4(aq)} \label{4a}\]
Cuando este proceso alcanza el equilibrio (lo que requiere que algún sólido esté presente), podemos escribir (dejando fuera los "(aq) s” por simplicidad)
\[Ag_2CrO_{4(s)} \rightleftharpoons 2 Ag^+ + CrO^{2–}_{4} \label{4b}\]
La constante de equilibrio es formalmente
\[K = \dfrac{[Ag^+]^2[CrO_4^{2–}]}{[Ag_2CrO_{4(s)}]} = [Ag^+]^2[CrO_4^{2–}] \label{5a}\]
Pero debido a que las sustancias sólidas no aparecen normalmente en las expresiones de equilibrio, la constante de equilibrio para este proceso es
\[[Ag^+]^2 [CrO_4^{2–}] = K_s = 2.76 \times 10^{–12} \label{5b}\]
Debido a que las constantes de equilibrio de este tipo se escriben como productos, las K resultantes se conocen comúnmente como productos de solubilidad, denotadas por\(K_s\) o\(K_{sp}\).
Estrictamente hablando, las unidades de concentración no aparecen en expresiones constantes de equilibrio. Sin embargo, muchos instructores prefieren que los estudiantes los muestren de todos modos, especialmente cuando usan productos de solubilidad para calcular concentraciones. Si esto se hace,\(K_s\) en Ecuación\(\ref{5b}\) tendría unidades de mol 3 L —3.
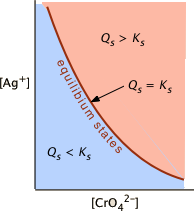
Equilibrio y no equilibrio en sistemas de solubilidad
Una expresión como [Ag +] 2 [CrO 4 2—] se conoce generalmente como un producto iónico, siendo este el producto iónico para cromato de plata. Un producto iónico puede tener en principio cualquier valor positivo, dependiendo de las concentraciones de los iones involucrados. Sólo en el caso especial cuando su valor es idéntico a K s se convierte en el producto de solubilidad. Se dice que una solución en la que este es el caso está saturada. Por lo tanto, cuando
\[[Ag^+]^2 [CrO_4^{2–}] = 2.76 \times 10^{-12}\]
a la temperatura y presión a la que se aplica este valor\(K_s\) de, decimos que la “solución está saturada en cromato de plata”.
Una solución debe estar saturada para estar en equilibrio con el sólido. Esta es una condición necesaria para el equilibrio de solubilidad, pero no es suficiente por sí misma. El verdadero equilibrio químico solo puede ocurrir cuando todos los componentes están presentes simultáneamente. Un sistema de solubilidad puede estar en equilibrio solo cuando parte del sólido está en contacto con una solución saturada de sus iones. No apreciar esto es una causa muy común de errores en la resolución de problemas de solubilidad.
Soluciones subsaturadas y sobresaturadas
Si el producto iónico es menor que el producto de solubilidad, el sistema no está en equilibrio y no puede estar presente ningún sólido. Se dice que tal solución está infrasaturada. Una solución sobresaturada es aquella en la que el producto iónico excede al producto de solubilidad. Una solución supersaturada no está en equilibrio, y normalmente no puede estar presente ningún sólido en dicha solución. Si se agrega algo del sólido, los iones en exceso precipitan y hasta lograr el equilibrio de solubilidad.
Cómo conocer el estado de saturación de una solución
Esto es solo una cuestión simple de comparar el producto iónico\(Q_s\) con el producto de solubilidad\(K_s\). S o para el sistema
\[Ag_2CrO_{4(s)} \rightleftharpoons 2 Ag^+ + CrO_4^{2–} \label{4ba}\]
una solución en la que\(Q_s < K_s\) (i.e.,\(K_s /Q_s > 1\)) está subsaturada (sombreado azul) y el no sólido estará presente. Las combinaciones de [Ag +] y [CrO 4 2—] que corresponden a una solución saturada (y por lo tanto al equilibrio) se limitan a las descritas por la línea curva. El área rosa a la derecha de esta curva representa una solución sobresaturada.
Se encontró que una muestra de agua subterránea que se ha filtrado a través de una capa de yeso (CaSO 4, K s = 4.9E—5 = 10 —4.3) es 8.4E—5 M en Ca 2 + y 7.2E—5 M en SO 4 2—. ¿Cuál es el estado de equilibrio de esta solución con respecto al yeso?
Solución
El producto iónico
\[Q_s = (8.4 \times 10^{–5})(7.2 \times 10^{-5}) = 6.0 \times 10^{–4}\]
excede\(K_s\), por lo que la relación K s/Q s > 1 y la solución está sobresaturada en CaSO 4.
¿Cómo se determinan las solubilidades?
Hay dos métodos principales, ninguno de los cuales es tan confiable para sales escasamente solubles:
- Evaporar una solución saturada del sólido a sequedad, y pesar lo que queda.
- Mida la conductividad eléctrica de la solución saturada, que será proporcional a las concentraciones de los iones.
Cómo se relacionan las solubilidades con los productos de solubilidad
La solubilidad (por la cual usualmente nos referimos a la solubilidad molar) de un sólido se expresa como la concentración del “sólido disuelto” en una solución saturada. En el caso de un sólido simple 1:1 como AgCl, esto solo sería la concentración de Ag + o Cl — en la solución saturada. Sin embargo, para una estequiometría más complicada como el cromato de plata, la solubilidad sería solo la mitad de la concentración de Ag +.
Por ejemplo, denotemos la solubilidad de Ag 2 CrO 4 como\(S\) mol L —1. Entonces para una solución saturada, tenemos
- \([Ag^+] = 2S\)
- \( [CrO_4^{2–}] = S\)
Sustituyendo esto en la ecuación\(\ref{5b}\) anterior,
\[(2S)^2 (S) = 4S^3 = 2.76 \times 10^{–12}\]
\[S= \left( \dfrac{K_s}{4} \right)^{1/3} = (6.9 \times 10^{-13})^{1/3} = 0.88 \times 10^{-4} \label{6a}\]
así la solubilidad es\(8.8 \times 10^{–5}\; M\).
Obsérvese que la relación entre la solubilidad y la constante del producto de solubilidad depende de la estequiometría de la reacción de disolución. Por esta razón no tiene sentido comparar las solubilidades de dos sales que tienen las fórmulas\(A_2B\) y\(AB_2\), sobre la base de sus\(K_s\) valores.
No tiene sentido comparar las solubilidades de dos sales que tienen fórmulas diferentes en base a sus\(K_s\) valores.
bajo estas condiciones.
Solución
moles de soluto en 100 mL; S = 0.0016 g/78.1 g/mol = 2.05E-5 mol
S = 2.05E—5 mol/0.100 L = 2.05E-4 M
K s = [Ca 2 +] [F —] 2 = (S) (2 S) 2 = 4 × (2.05E—4) 3 = 3.44E—11
Estimar la solubilidad de La (IO 3) 3 y calcular la concentración de yodato en equilibrio con yodato de lantano sólido, para lo cual K s = 6.2 × 10 —12.
Solución
La ecuación para la disolución es
\[La(IO_3)_3 \rightleftharpoons La^{3+ }+ 3 IO_3^–\]
Si la solubilidad es S, entonces las concentraciones de equilibrio de los iones serán
[La 3 +] = S y [IO 3 —] = 3 S. Entonces K s = [La 3+] [IO 3 —] 3 = S (3 S) 3 = 27 S 4
27 S 4 = 6.2 × 10 —12, S = ((6.2 ÷ 27) × 10 —12) ¼ = 6.92 × 10 —4 M
[IO 3 —] = 3 S = 2.08 × 10 —5 (M)
El cadmio es un contaminante ambiental altamente tóxico que ingresa a las aguas residuales asociadas con la fundición de zinc (Cd y Zn comúnmente ocurren juntos en minerales de ZnS) y en algunos procesos de galvanoplastia. Una forma de controlar el cadmio en las corrientes efluentes es agregar hidróxido de sodio, el cual precipita Cd (OH) 2 insoluble (K s = 2.5E—14). Si 1000 L de una determinada agua residual contiene Cd 2+ a una concentración de 1.6E—5 M, ¿qué concentración de Cd 2+ permanecería después de la adición de 10 L de solución de NaOH 4 M?
Solución
Al igual que con la mayoría de los problemas del mundo real, esto se aborda mejor como una serie de problemas más pequeños, haciendo aproximaciones simplificadas según sea apropiado.
Volumen de agua tratada: 1000 L + 10 L = 1010 L
Concentración de OH — en adición a 1000 L de agua pura:
(4 M) × (10 L)/(1010 L) = .040 M
Concentración inicial de Cd 2 + en 1010 L de agua:
(1.6E—5 M) x (100/101) ≈ 1.6E—5 M
La forma más fácil de abordar esto es comenzar asumiendo que se forma una cantidad estequiométrica de Cd (OH) 2, es decir, todo el Cd 2 + se precipita.
| Concentraciones | [Cd 2+], M | [OH —], M |
|---|---|---|
| inicial | 1.6E—5 | 0.04 |
| cambiar | —1.6E—5 | —3.2E—5 |
| final: | 0 | 0.04 — 3.2E—5 ≈ .04 |
Ahora “enciende el equilibrio” — encuentra la concentración de Cd 2 + que puede existir en una solución 0.04 M OH —:
| Concentraciones | [Cd 2+], M | [OH —], M |
|---|---|---|
| inicial | o | 0.04 |
| cambiar | + x | +2 x |
| en equilibrio | x | 0.04 + 2 x ≈ .04 |
Sustituir estos valores en la expresión del producto de solubilidad:
\[Cd(OH)_{2(s) } = [Cd^{2+}] [OH^–]^2 = 2.5 \times 10^{–14}\]
\[[Cd^{2+}] = \dfrac{2.5 \times 10^{–14}}{ 16 \times 10^{–4}} = 1.6 \times 10^{–13}\; M\]
Tenga en cuenta que el efluente ahora será muy alcalino:
\[pH = 14 + \log 0.04 = 12.6\]
por lo que para cumplir con los estándares ambientales se debe agregar una cantidad equivalente de ácido fuerte para neutralizar el agua antes de que se libere.
Todo solo una simplificación de la realidad
Las relaciones simples entre K s y solubilidad molar señaladas anteriormente, y los ejemplos de cálculo aquí dados, no pueden ser confiados para dar respuestas correctas. Algunas de las razones de esto se explican en la Parte 2 de esta lección, y tienen que ver principalmente con la disociación incompleta de muchas sales y con la formación de complejos en presencia de aniones como Cl —y OH —. La situación se describe muy bien en el artículo ¿Qué debemos enseñar a los principiantes sobre los productos de solubilidad y solubilidad? de Stephen Hawkes (J Chem Educ. 1998 75 (9) 1179-81). Consulta también el artículo anterior de Meites, Pode y Thomas ¿Están relacionados las solubilidades y los productos de solubilidad? (J Chem Educ. 1966 43 (12) 667-72).
Resulta que los equilibrios de solubilidad en la mayoría de las veces implican muchos procesos competidores y su tratamiento riguroso puede ser bastante complicado. Sin embargo, es importante que los estudiantes dominen estos ejemplos sobresimplificados. Sin embargo, ¡también es importante que no se tomen demasiado en serio!
El efecto común de iones
Desde hace tiempo se sabe que la solubilidad de una sustancia iónica escasamente soluble disminuye notablemente en una solución de otro compuesto iónico cuando las dos sustancias tienen un ion en común. Esto es justo lo que se esperaría sobre la base del Principio Le Chatelier; siempre que el proceso
\[CaF_{2(s)} \rightleftharpoons Ca^{2+} + 2 F^– \label{7}\]
está en equilibrio, la adición de más ion fluoruro (en forma de NaF altamente soluble) desplazará la composición hacia la izquierda, reduciendo la concentración de Ca 2 +, y reduciendo así efectivamente la solubilidad del sólido. Podemos expresar esto cuantitativamente señalando que la expresión del producto de solubilidad
\[[Ca^{2+}][F^–]^2 = 1.7 \times 10^{–10} \label{8}\]
debe mantenerse siempre, aunque algunas de las especies iónicas involucradas provengan de fuentes distintas al CaF 2 (s). Por ejemplo, si se agrega cierta cantidad x de ion fluoruro a una solución inicialmente en equilibrio con CaF 2 sólido, tenemos
- \([Ca^{2+}] = S\)
- \([F^–] = 2S + x\)
para que
\[K_s = [Ca^{2+}][ F^–]^2 = S (2S + x)^2 . \label{9a}\]
\[K_s ≈ S x^2 \]
o
\[S ≈ \dfrac{K_s}{x^2} \label{9b}\]
Los estudiantes de nivel universitario deben ser capaces de derivar estas relaciones para sólidos derivados de iones de cualquier estequiometría.
Las gráficas que se muestran a continuación ilustran el efecto iónico común para el cromato de plata ya que la concentración de iones cromato se incrementa mediante la adición de un cromato soluble tal como\(Na_2CrO_4\).
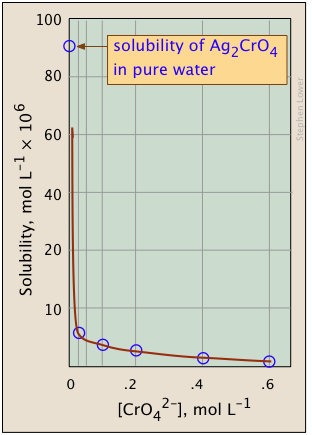
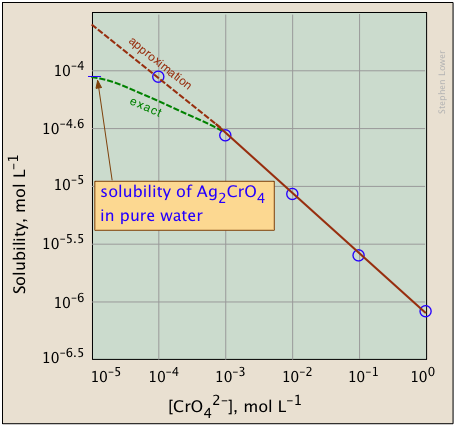
¿Qué tiene de diferente la trama de la derecha? Si miras cuidadosamente las escalas, verás que ésta está trazada logarítmicamente (es decir, en potencias de 10.) Observe cómo un rango de valores mucho más amplio puede mostrar en una gráfica logarítmica. El objetivo de mostrar este par de gráficas es ilustrar la gran utilidad de las gráficas logarítmicas de concentración en los cálculos de equilibrio en las que aproximaciones simples (como la realizada en Ecuación\(\ref{9b}\) pueden producir líneas rectas dentro del rango de valores para los que la aproximación es válida.
Calcular la solubilidad del sulfato de estroncio (K s = 2.8 × 10 —7) en
- agua pura y
- en una solución de 0.10 mol L —1 de\(Na_2SO_4\).
\[S = \sqrt{K_s} = \sqrt{ 2.8 \times 10^{–7} } = 5.3 \times 10^{–4}\]
(b) En 0.10 mol L —1 Na 2 SO 4, tenemos
= [Sr 2 +] [SO 4 2—] = S × (0.10 + S) = 2.8 × 10 —7Debido a que S es insignificante en comparación con 0.10 M, hacemos la aproximación
= [Sr 2 +] [SO 4 2—] ≈ S × (0.10 M) = 2.8 × 10 —7por lo
Esto es aproximadamente 100 veces más pequeño que el resultado de (a).
Precipitaciones y separaciones selectivas
Las diferencias en la solubilidad son ampliamente utilizadas para eliminar selectivamente una especie de una solución que contiene varios tipos de iones.
Los productos de solubilidad de AgCl y Ag 2 CrO 4 son 1.8E—10 y 2.0E—12, respectivamente. Supongamos que se agrega gota a gota una solución diluida de AgnO 3 a una solución que contiene 0.001 M Cl — y 0.01 M CrO 4 2—.
- ¿Qué sólido, AgCl o Ag 2 CrO 4, precipitará primero?
- ¿Qué fracción del primer anión se habrá eliminado cuando el segundo apenas comience a precipitar? Descuidar cualquier cambio de volumen.
Solución
Las concentraciones de iones de plata requeridas para precipitar las dos sales se encuentran sustituyendo en las expresiones de producto de solubilidad apropiadas:
- para precipitar AgCl: [Ag +] = 1.8E-10/.001 = 1.8E-7 M
- precipitar Ag 2 CrO 4: [Ag +] = (2.0E-12/.01) ½ = 1.4E—5 M
El primer sólido que se forme a medida que aumenta la concentración de Ag + será AgCl. Finalmente, la concentración de Ag + alcanza 1.4E-5 M y Ag 2 CrO 4 comienza a precipitar. En este punto la concentración de ion cloruro en la solución será de 1.3E-5 M que es aproximadamente 13% de la cantidad originalmente presente.
El ejemplo anterior es la base de la titulación Mohr de cloruro por Ag +, comúnmente realizada para determinar la salinidad de las muestras de agua. El punto de equivalencia de esta titulación de precipitación ocurre cuando no se forma más AgCl, pero no hay manera de observarlo directamente en presencia del AgCl blanco que se suspende en el recipiente. Antes de comenzar la titulación, se agrega una pequeña cantidad de K 2 CrO 4 a la solución. Ag 2 CrO 4 es de color rojo-naranja, por lo que su formación, que señala el final aproximado de la precipitación de AgCl, se puede detectar visualmente.
Equilibrios competidores que involucran sólidos
La expresión de solubilidad es probablemente la excepción y no la regla. Tales equilibrios suelen estar en competencia con otras reacciones con especies como H + u OH —, agentes complejantes, oxidación-reducción, formación de otras especies escasamente solubles o, en el caso de carbonatos y sulfitos, de productos gaseosos. Los tratamientos exactos de estos sistemas pueden ser extremadamente complicados, involucrando la solución de grandes conjuntos de ecuaciones simultáneas. Para la mayoría de los propósitos prácticos es suficiente reconocer las tendencias generales, y realizar cálculos aproximados.
Las sales de ácidos débiles son solubles en ácidos fuertes, pero los ácidos fuertes no disolverán sales de ácidos fuertes
La solubilidad de una sal escasamente soluble de un ácido o base débil dependerá del pH de la solución. Para entender la razón de esto, considere una sal hipotética MA que se disuelve para formar un catión M + y un anión A, que también es la base conjugada de un HA ácido débil. El hecho de que el ácido sea débil significa que los iones hidrógeno (siempre presentes en soluciones acuosas) y los cationes M+ estarán compitiendo por el A —:

Cuanto más débil sea el ácido HA, más fácilmente tendrá lugar la reacción, engulliendo así A — iones. Si se pone a disposición un exceso de H + mediante la adición de un ácido fuerte, se consumirán aún más iones A —, eventualmente invirtiendo la reacción
tendrá lugar la reacción, engulliendo así A — iones. Si se pone a disposición un exceso de H + mediante la adición de un ácido fuerte, se consumirán aún más iones A —, eventualmente invirtiendo la reacción , haciendo que el sólido se disuelva.
, haciendo que el sólido se disuelva.

En , por ejemplo, los iones sulfato reaccionan con los iones calcio para formar CaSO 4 insoluble. La adición de un ácido fuerte como el HCl (que está totalmente disociado
, por ejemplo, los iones sulfato reaccionan con los iones calcio para formar CaSO 4 insoluble. La adición de un ácido fuerte como el HCl (que está totalmente disociado ) no tiene ningún efecto porque el CaCl 2 es soluble. Aunque H + puede protonar algunos iones SO 4 2— para formar sulfato de hidrógeno (“bisulfato”) HSO 4, este ácido anfolito es demasiado débil para revertirse
) no tiene ningún efecto porque el CaCl 2 es soluble. Aunque H + puede protonar algunos iones SO 4 2— para formar sulfato de hidrógeno (“bisulfato”) HSO 4, este ácido anfolito es demasiado débil para revertirse al extraer una fracción significativa de iones sulfato de CaSO 4 (s).
al extraer una fracción significativa de iones sulfato de CaSO 4 (s).
Calcular la concentración de ion aluminio en una solución que está en equilibrio con hidróxido de aluminio cuando el pH se mantiene en 6.0.
Los equilibrios son
\[Al(OH)_3 \rightleftharpoons Al^{3+} + 3 OH^–\]
con
\[K_s = 1.4 \times 10^{–34}\]
y
\[H_2O \rightleftharpoons H^+ + OH^–\]
con
\[K_w = 1 \times 10^{–14}\]
Sustituyendo la expresión de equilibrio por la segunda de éstas en la de la primera, obtenemos
\[[OH^–]^3 = \left( \dfrac{K_w}{ [H^+]}\right)^3 = \dfrac{K_s}{[Al^{3+}]}\]
(1.0 × 10 —14)/(1.0 × 10 —6) 3 = (1.4 × 10 —24)/[Al 3 +]
de donde encontramos
\[[Al^{3+}] = 1.4 \times 10^{–10}\; M\]
Formación de un precipitado competidor
Si dos aniones diferentes compiten con un solo catión para formar dos posibles precipitados, el resultado depende no sólo de las solubilidades de los dos sólidos, sino también de las concentraciones de los iones relevantes.

Este tipo de competencias son especialmente importantes en las aguas subterráneas, las cuales adquieren solutos de diversas fuentes a medida que pasan a través de capas de sedimentos que tienen diferentes composiciones. Como muestra el siguiente ejemplo, los equilibrios competidores de este tipo son muy importantes para comprender los procesos geoquímicos que involucran la formación y transformación de depósitos minerales.
Supongamos que el agua subterránea que contiene 0.001 M F — y 0.0018 M CO 3 2— se filtra a través de un sedimento que contiene calcita, CaCo 3. ¿La calcita será reemplazada por fluorita, CaF 2?
Los dos equilibrios de solubilidad son
\[\ce{CaCO3 <=> Ca^{2+} + CO3^{2–} \quad K_s = 10^{–8.1}\]
\[\ce{CaF2 <=> Ca^{2+} + 2 F^{–} \quad K_s = 10^{–10.4}\]
Solución:
El equilibrio entre los dos sólidos y los dos aniones es
\[CaCO_3 + 2 F^–\rightleftharpoons CaF_2 + CO_3^{2–}\]
Esta es solo la suma de la reacción de disolución para CaCo 3 y la inversa de la de CaF 2, por lo que la constante de equilibrio es
\[K = \dfrac{[CO_3^{2–}]}{ [F^–]^2} = \dfrac{10^{–8.1}}{ 10^{–10.4}} = 200\]
Es decir, los dos sólidos sólo pueden coexistir si el cociente de reacción Q ≤ 200. Sustituyendo las concentraciones de iones dadas, encontramos que
\[Q = \dfrac{0.0018}{0.0012} = 1800\]
Desde Q > K, podemos concluir que la calcita no cambiará a fluorita.
Formación de iones complejos
La mayoría de los iones de metales de transición poseen orbitales d vacíos que son suficientemente bajos en energía para poder aceptar pares de electrones de donantes de electrones de cationes, lo que resulta en la formación de un ion complejo unido de manera covalentía. Incluso las especies neutras que tienen un par de electrones sin unión pueden unirse a los iones de esta manera. El agua es un donador de electrones activo de este tipo, por lo que existen soluciones acuosas de iones como Fe 3 + (aq) y Cu 2 + (aq) como los complejos octaédricos Fe (H 2 O) 6 3+ y Cu (H 6 O) 6 2+, respectivamente.
Muchos de los comentarios anteriores sobre la relación entre K s y solubilidad también se aplican a los cálculos que involucran la formación de complejos. Ver artículo de Stephen Hawkes Los cálculos de complejación son peores que inútiles (“... hasta el punto del absurdo... y no se debe enseñar” en cursos introductorios.) (J Chem Educ. 1999 76 (8) 1099-1100). No obstante, es muy importante que entiendas los principios esbozados en esta sección.
H 2 O es solo un posible donante de electrones; NH 3, CN — y muchas otras especies (conocidas colectivamente como ligandos) poseen pares solitarios que pueden ocupar orbitales d vacíos en un ion metálico. Muchos de estos se unen mucho más estrechamente al metal que el H 2 O, que sufrirá desplazamiento y sustitución por uno o más de estos ligandos si están presentes en una concentración suficientemente alta.
Si un sólido escasamente soluble se pone en contacto con una solución que contiene un ligando que puede unirse al ion metálico mucho más fuertemente que H 2 O, entonces se favorecerá la formación de un ion complejo y la solubilidad del sólido será mayor. Quizás el ejemplo más comúnmente visto de esto ocurre cuando se agrega amoníaco a una solución de nitrato de cobre (II), en la que el ion Cu 2 + (ac) es en sí mismo el ion complejo hexaaquo complejo que se muestra a la izquierda:

Debido a que el amoníaco es una base débil, lo primero que observamos es la formación de un precipitado turbio de Cu (OH) 2 en la solución azul. A medida que se agrega más amoníaco, este precipitado se disuelve, y la solución se vuelve un azul intenso intenso, que es el color del hexamminocobre (II) y las otras especies relacionadas como Cu (H 2 O) 5 (NH 3) 2+, Cu (H 2 O) 4 (NH 3) 2 2+, etc.

En muchos casos, el agente complejante y el anión de la sal escasamente soluble son idénticos. Esto es particularmente probable que ocurra con cloruros insolubles, y significa que la adición de cloruro para precipitar un ion metálico como Ag + producirá un precipitado al principio, pero después de que se haya agregado exceso de Cl, el precipitado se volverá a disolver a medida que se formen iones complejos.
Algunos sistemas de solubilidad importantes
En esta sección se discuten los equilibrios de solubilidad que se relacionan con algunos aniones muy comunes de sales metálicas. Estos son especialmente pertinentes a los tipos de separaciones que la mayoría de los estudiantes universitarios están obligados a llevar a cabo (¡y entender!) en sus cursos de laboratorio de primer año.
Solubilidad de óxidos e hidróxidos
Tanto los óxidos metálicos como los hidróxidos forman soluciones que contienen iones OH. Por ejemplo, las solubilidades del óxido e hidróxido de magnesio [escasamente solubles] están representadas por
\[Mg(OH)_{2(s)} → Mg^{2+} + 2 OH^– \label{10}\]
\[MgO_{(S)} + H_2O → Mg^{2+} + 2 OH^– \label{11}\]
Si escribes las expresiones de producto de solubilidad para estas dos reacciones, verás que son idénticas en forma y valor.
Recordemos que pH = —log 10 [H +], de manera que [H +] = 10 —pH.
Uno podría esperar ingenuamente que la disolución de un óxido como MgO produciría como uno de sus productos el ion óxido O 2+. Pero el ion óxido es una base tan fuerte que agarra un protón del agua, formando en su lugar dos iones hidróxido:
\[O^{2+} + H_2O → 2 OH^–\]
Este es un ejemplo de la regla de que el ion hidróxido es la base más fuerte que puede existir en solución acuosa. 2" es una mezcla de equilibrio de moléculas de CO 2 hidratadas y ácido carbónico. Para mantener las cosas lo más simples posible, no vamos a distinguir entre ellas en lo que sigue, y solo usaremos la fórmula H 2 CO 3 para representar las dos especies colectivamente.
Los otros metales del Grupo 2, especialmente el Mg, junto con el hierro y varios otros elementos de transición también se encuentran en los sedimentos carbonatados. Cuando la lluvia cae por el aire, absorbe el dióxido de carbono atmosférico, una pequeña porción del cual reacciona con el agua para formar ácido carbónico. Así, toda el agua pura en contacto con el aire se vuelve ácida, alcanzando finalmente un pH de 5.6.
Como se señaló anteriormente, el equilibrio entre los iones bicarbonato y carbonato depende del pH. Dado que la escala de pH es logarítmica, tiene sentido (y simplifica enormemente la construcción de la parcela) emplear una escala logarítmica para las concentraciones. La gráfica que se muestra a continuación corresponde a una concentración total del sistema carbonato-sistema de 10 —3 M, la cual es representativa de muchas aguas subterráneas. Para las aguas de ríos y lagos, 10 —5 M serían más típicos; esto simplemente desplazaría las curvas hacia abajo sin afectar sus formas.

Los puntos 1 y 2 donde las curvas adyacentes se superponen corresponden a los dos pK's. Recordemos que cuando el pH es el mismo que el pK, las concentraciones de las dos especies conjugadas son idénticas y la mitad de la concentración total del sistema. Esto coloca los puntos de cruce en log 0.5 = —0.3 por debajo del nivel de concentración del sistema.
Una solución 10 —3 M de bicarbonato de sodio tendría un pH denotado por el punto 3, constituyendo [H 2 CO 3] y [CO 3 2—] solo 1% (10 —5 M) del sistema. Esto corresponde al equilibrio
\[2 HCO_3^– \rightleftharpoons H_2CO_3 + CO_3^{2–}\]
Carbonates act as bases and, as such, react with acids. Thus, the portion of the global water cycle that transports carbon from the air into natural waters constitutes a gigantic acid-base reaction that yields hydrogen carbonate ions, commonly referred to as bicarbonate. The natural waters that result have pH values between 6 and 10 and are essentially solutions of bicarbonates.
Limestone caves and sinkholes
When rainwater permeates into the soil, it can become even more acidic owing to the additional CO2 produced by soil organisms. Also, the deeper the water penetrates, the greater its hydrostatic pressure and the more CO2 it can hold, further increasing its acidity. If this water then works its way down through the fissures and cracks within a limestone layer, it will dissolve some of limestone, leaving void spaces which may eventually grow into limestone caves or form sinkholes that can swallow up cars or houses.
A well-known feature of limestone caves is the precipitated carbonate formations that decorate the ceilings and floors. These are known as stalactites and stalagmites, respectively. When water emerges from the ceiling of a cave that is open to the atmosphere, some of the excess CO2 it contains is released as it equilibrates with the air. This raises its pH and thus reduces the solubility of of the carbonates, which precipitate as stalactites. Some of the water remains supersaturated and does not precipitate until it drips to the cave floor, where it builds up the stalagmite formations.
Hard Water
This term refers to waters that, through contact with rocks and sediments in lakes, streams, and especially in soils (groundwaters), have acquired metallic cations such as Ca2+, Mg2+, Fe2+, Fe3+, Zn2+ Mn2+, etc. Owing to the ubiquity of carbonate sediments, the compensating negative charge is frequently supplied by the bicarbonate ion HCO3–, but other anions such as SO42–, F–, Cl–, PO43– and SiO42– may also be significant.
Solid bicarbonates are formed only by Group 1 cations and all are readily soluble in water. But because HCO3– is amphiprotic, it can react with itself to yield carbonate:
\[2 HCO_3^– → H_2O + CO_3^[2–} + CO_{2(g)}\]
If bicarbonate-containing water is boiled, the CO2 is driven off, and the equilibrium shifts to the right, causing any Ca2+ or similar ions to form a cloudy precipitate. If this succeeds in removing the "hardness cations", the water has been "softened". Such water is said to possess carbonate hardness, sometimes known as "temporary hardness". Waters in which anions other than HCO3– predominate cannot be softened by boiling, and thus possess non-carbonate hardness or "permanent hardness".
Hard waters present several kinds of problems, both in domestic and industrial settings:
- Waters containing dissolved salts leave solid deposits when they evaporate. Residents of areas having hard water (about 85 percent of the U.S.) notice evaporative deposits on shower walls, in teakettles, and on newly-washed windows, glassware, and vehicles.
- Much more seriously from an economic standpoint, evaporation of water in boilers used for the production of industrial steam leaves coatings on the heat exchanger surfaces that impede the transfer of heat from the combustion chamber, reducing the thermal transfer efficiency. The resultant overheating of these surfaces can lead to their rupture, and in the case of high-pressure boilers, to disastrous explosions. In the case of calcium and magnesium carbonates, the process is exacerbated by the reduced solubility of these salts at high temperatures. Removal of boiler scales is difficult and expensive.
- Municipal water supplies in hard-water areas tend to be supersaturated in hardness ions. As this water flows through distribution pipes and the plumbing of buildings, these ions often tend to precipitate out on their interior surfaces. Eventually, this scale layer can become thick enough to restrict or even block the flow of water through the pipes. When scale deposits within appliances such as dishwashers and washing machines, it can severely degrade their performance.
- Cations of Group 2 and above react with soaps, which are sodium salts of fatty acids such as stearic acid, C17H35COOH. The sodium salts of such acids are soluble in water, which allows them to dissociate and act as surfactants:
\[C_{17}H_{35}COONa → C_{17}H_{35}COO^– Na^+\]
but the presence of polyvalent ions causes them to form precipitates
\[2 C_{17}H_{35}COO^– + Ca^{2+} → (C_{17}H_{35}COO^–)_2Ca_{(s)}\]
Calcium stearate is less dense than water, so it forms a scum that floats on top of the water surface; anyone who lives in a hard-water area is likely familiar with the unsightly "bathtub rings" it leaves around the high-water mark or the shower-wall stains.
Solubility Complications
All heterogeneous equilibria, on close examination, are beset with complications. But solubility equilibria are somewhat special in that there are more of them. Back in the days when the principal reason for teaching about solubility equilibria was to prepare chemists to separate ions in quantitative analysis procedures, these problems could be mostly ignored. But now that the chemistry of the environment has grown in importance — especially that relating to the ocean and natural waters — there is more reason for chemical scientists to at least know about the limitations of simple solubility products. This section will offer a quick survey of the most important of these complications, while leaving their detailed treatment to more advanced courses.
Tabulated Ks values are notoriously unreliable
Many of the \(K_s\) values found in tables were determined prior to 1940 (some go back to the 1880s!) at a time before highly accurate methods became available. Especially suspect are many of those for highly insoluble salts which are more difficult to measure. A table showing the variations in \(K_{sp}\) values for the same salts among ten textbooks was published by Clark and Bonikamp in J Chem Educ. 1998 75(9) 1183-85.A good An example that used a variety of modern techniques to measure the solubility of silver chromate was published by A.L. Jones et al in the Australian J. of Chemistry, 1971 24 2005-12.
Generations of chemistry students have amused themselves by comparing the disparate Ks values to be found in various textbooks and table. In some cases, they differ by orders of magnitude. There are several reasons for this in addition to the ones described in detail further on.
- The most direct methods of measuring solubilities tend to not be very accurate for sparingly soluble salts. Two-significant figure precision is about the best one can hope in a single measurement.
- Many insoluble salts can exist in more than one crystalline form (polymorphs), and in some cases also as amorphous solids. Precipitation under different conditions (in the presence of different ions, at different temperatures, etc.) can yield different or mixed polymorphs.
- Other ions present in the solution can often get incorporated into the crystalline solid, usually replacing an ion of similar size (substitutional solid solutions). When this happens, it is no longer valid to write the equilibrium condition as a simple "product". This is very common in mineral deposits, and an important consideration in geochemistry,
Most salts are not Completely Dissociated in Water
The dissolution of cadmium iodide is water is commonly represented as
\[CdI_{2(s)} → Cd^{2+} + 2 I^–\]
Firstly, they combine to form neutral, largely-covalent molecular species:
\[Cd^{2+}_{(aq)} + 2 I^–_{(aq)} → CdI_{2(aq)}\]
This non-ionic form accounts for 78% of the Cd present in the solution! In addition, they form a molecular ion \(CdI^–_{(aq)}\) according to the following scheme:
| \(CdI_{2(s)} \rightleftharpoons Cd^{2+} + 2 I^–\) | \(K_1 = 10^{–3.9}\) |
| \(Cd^{2+} + I^– \rightleftharpoons CdI^+\) | \(K_2= 10^{+2.3}\) |
| \(CdI2_{(s)} \rightleftharpoons CdI^++ I^–\) | \(K = 10^{–1.6} = 0.023\) |
The data shown Tables \(\PageIndex{1}\) and \(\PageIndex{2}\) are taken from the article Salts are Mostly NOT Ionized by Stephen Hawkes: 1996 J Chem Educ. 73(5) 421-423. This fact was stated by Arrhenius in 1887, but has been largely ignored and is rarely mentioned in standard textbooks.
As a consequence, the concentration of "free" Cd2+(aq) in an aqueous cadmium iodide solution is only about 2% of the value you would calculate by taking K1 as the solubility product. The principal component of such as solution is actually [covalently-bound] CdI2(aq). It turns out that many salts, especially those of metals beyond Group 2, are similarly only partially ionized in aqueous solution:
| salt | molarity | % cation | other species |
|---|---|---|---|
| KCl | 0.52 | 95 | KCl(aq) 5% |
| MgSO4 | 0.04 | 58 | MgSO4(aq) 42% |
| CaCl2 | 0.44 | 70 | CaCl+(aq) 30% |
| CuSO4 | 0.045 | 56 | CuSO4(aq) 44% |
| CdI2 | 0.50 | 2 | CdI2(aq) 76%, CdI–(aq) 22% |
| FeCl3 | 0.1 | 10 | FeCl2+(aq) 42%, FeCl2(aq) 40%, FeOH2+(aq) 6%, Fe(OH)2+(aq) 2% |
If you are enrolled in an introductory course and do not plan on taking more advanced courses in chemistry or biochemistry, you can probably be safe in ignoring this, since your instructor and textbook likely do so. However, if you expect to do more advanced work or teach, you really should take note of these points, since few textbooks mention them.
Formation of Hydrous Complexes
Transition metal ions form a large variety of complexes with H2O and OH–, both of which have electron-pairs available to coordinate with the central ion. This gives rise to a large variety of soluble species that are in competition with an insoluble solid. Because of this, a single equilibrium constant (solubility product) cannot describe the behavior of a solid such as Fe(OH)3, which we summarize here as an example.
Aquo complexes: The electrostatic field of the positively-charged metal ion enhances the acidic nature of these H2O molecules, encouraging them to shed a proton and leaving OH– groups in their place.
\[Fe(H_2O)_6^{3+} → Fe(H_2O)_5(OH)^{2+}+H^+\]
This is just the first of a series of similar reactions, each one having a successively smaller equilibrium constant:
\[Fe(H_2O)_5(OH)^{2+}→ Fe(H_2O)_4(OH)_2^+→ Fe(H_2O)_3(OH)_3 → Fe(H_2O)_2(OH)_4^-\]
Hydroxo complexes: But there's more: when the hydroxide ion acts as a ligand, it gives rise to a series of hydroxo complexes, of which the insoluble Fe(OH)3 can be considered a member:
| Fe3+ + 3 OH– → Fe(OH)3(s) | 1/Ks = 1038 |
| Fe3+ + H2O → Fe(OH)2+ + H+ | K = 10–2.2 |
| Fe3+ + 2H2O → FeOH+ + 2H+ | K = 10–6.7 |
| Fe3+ + 4H2O → Fe(OH)4– + 4H+ | K = 10–23 |
| 2Fe3+ + 2H2O → Fe2(OH)24+ + 2H+ | K = 10–2.8 |

Los equilibrios enumerados anteriormente involucran iones H + y OH —, y por lo tanto son dependientes del pH, como lo ilustran las líneas rectas en la parcela, cuyas pendientes reflejan la dependencia del pH de las especies iónicas correspondientes. A cualquier pH dado, el equilibrio con Fe (OH) 3 sólido es controlado por las especies iónicas que tienen la concentración más alta a cualquier pH dado. Por lo tanto, las líneas correspondientes en la parcela delimitan la región (indicada por el sombreado naranja) en la que puede existir el sólido.
Interacciones iónicas: El “efecto iónico no común”
Una sal escasamente soluble será más soluble en una solución que contenga iones no participantes. Esto es justo lo contrario del efecto ion común, y al principio podría parecer bastante contrario a la intuición: ¿por qué agregar más iones de cualquier tipo haría que una sal sea más propensa a disolverse?
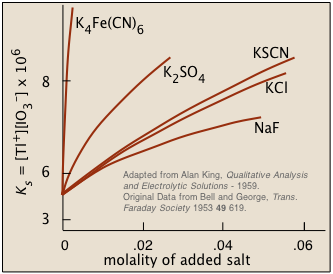
Figura\(\PageIndex{2}\) : Solubilidad del yodato de talio en soluciones que contienen sales disueltas
Una pista de la respuesta se puede encontrar en otro hecho: cuanto mayor es la carga del ion extraño, más pronunciado es el efecto. Esto nos dice que las interacciones interiónicas (y por lo tanto electrostáticas) deben jugar un papel. Los detalles son bastante complicados, pero la idea general es que todos los iones en solución, además de poseer aguas de hidratación apretadas, tienden a atraer iones de carga opuesta (” contra-iones “) a su alrededor. Esta “atmósfera” de contraiones es siempre bastante difusa, pero mucho menos (y más estrechamente ligada) cuando uno o ambos tipos de iones tienen mayores cargas. Desde la distancia, estos cuerpos de iones contraiones parecen ser casi eléctricamente neutros, lo que les impide interactuar entre sí (como para formar un precipitado).

El efecto general es reducir las concentraciones de los iones menos protegidos que están disponibles para combinarse para formar un precipitado. Decimos que las concentraciones termodinámicamente efectivas de estos iones son menores que sus concentraciones “analíticas”. Los químicos se refieren a estas concentraciones efectivas como actividades iónicas, y las denotan entre corchetes {Ag +} a diferencia de corchetes [Ag +] que se refieren a las concentraciones nominales o analíticas.
Si bien las concentraciones de iones en equilibrio con un sólido escasamente soluble son tan bajas que son esencialmente las mismas que las actividades, la presencia de otros iones a concentraciones de aproximadamente 0.001M o mayores puede reducir materialmente las actividades de los productos de disolución, permitiendo solubilidades para ser mayores de lo que los simples cálculos de equilibrio predecirían.
Las solubilidades medidas son promedios y dependen del tamaño
La naturaleza heterogénea de las reacciones de disolución conduce a una serie de efectos peculiares relacionados con la naturaleza de los equilibrios que involucran superficies. Estos surgen del hecho de que la tendencia de un sólido cristalino a disolverse dependerá de la cara o ubicación particular a partir de la cual se produzca la disolución. Dado que todos los cristales presentan una variedad de caras a la solución, un K s medido es realmente un promedio de valores para estas diversas caras.
Y debido a que muchas sales pueden exhibir diferentes formas externas dependiendo de las condiciones en las que se formen, los productos de solubilidad dependen de manera similar de estas condiciones.
Los cristales muy pequeños son más solubles que los grandes
Las moléculas o iones que están situados en los bordes o esquinas están menos fuertemente unidos al resto del sólido que los de las superficies planas y, en consecuencia, tenderán a disolverse más fácilmente. Así, la cara más a la izquierda en la retícula esquemática inferior tendrá más unidades moleculares ligadas al borde que las otras dos, y esta cara (11) será más soluble.
Esto significa, entre otras cosas, que los cristales más pequeños, en los que la relación de bordes y esquinas es mayor, tenderán a tener mayores valores de K s que los mayores. Como consecuencia, los cristales más pequeños tenderán a desaparecer en favor de los más grandes. A veces se hace uso práctico de esto cuando el precipitado inicialmente formado en un análisis químico o separación es demasiado fino para ser eliminado por filtración. La suspensión se mantiene a alta temperatura durante varias horas, durante que con el tiempo los cristalitos crecen en tamaño. A este procedimiento se le conoce a veces como digestión.
Formación de soluciones sobresaturadas
Contrario a lo que te hayan enseñado, los precipitados no se forman cuando el producto de concentración iónica alcanza el producto de solubilidad de una sal en una solución que es pura e inicialmente insaturada; para formar un precipitado a partir de una solución homogénea, se requiere cierto grado de sobresaturación. El grado de sobresaturación requerido para iniciar la precipitación puede ser sorprendentemente grande. Así, la formación de sulfato de bario BaSO 4 mediante la combinación de los dos tipos de iones no ocurre hasta que Q s excede K s por un factor de 160 o más. En parte, esto refleja el hecho de que la precipitación procede por una serie de reacciones que comienzan con la formación de un par iónico que eventualmente se convierte en un cúmulo iónico:
Ba 2 + + SO 4 2— → (BaSO 4) 0 → (BaSO 4) 2 0 → (BaSO 4) 3 0 → etc.
Debido a su neutralidad general, estos agregados no se estabilizan por hidratación, por lo que es más probable que se rompan que no. Pero algunos pueden eventualmente sobrevivir hasta que sean lo suficientemente grandes (pero aún de tamaño submicroscópico) para servir como núcleos de precipitación.
Muchas sustancias distintas a las sales forman soluciones supersaturadas, y algunas sales las forman más fácilmente que otras. Las soluciones supersaturadas se hacen fácilmente disolviendo el sólido hasta cerca de su límite de solubilidad en un disolvente calentado y luego dejándolo enfriar.
K s) y son inherentemente inestables; la caída de un cristal “semilla” del sólido en dicha solución generalmente iniciará una precipitación rápida. Pero como se explica a continuación, incluso una pequeña partícula de polvo puede ser suficiente. El truco de un viejo químico es usar la punta de una varilla agitadora de vidrio para raspar la superficie interna de un recipiente que contiene una solución sobresaturada; las partículas diminutas de vidrio que se liberan presumiblemente sirven como núcleos de precipitación.
El problema de nucleación: ¡la precipitación es [teóricamente] imposible!
Cualquier proceso en el que se forme una nueva fase dentro de una fase homogénea existente está acosado por el problema de nucleación: la más pequeña de estas nuevas fases —gotas de lluvia que se forman en el aire, pequeñas burbujas que se forman en un líquido en su punto de ebullición— son inherentemente menos estables que las más grandes, y por lo tanto tienden a desaparecer. Lo mismo ocurre con la formación de precipitados: si los cristales más pequeños son más solubles, entonces ¿cómo se puede formar el más pequeño, el primer cristal, en absoluto?
En cualquier solución iónica, pequeños grupos de iones con carga opuesta se forman continuamente mediante procesos de colisión ordinarios. Los más pequeños de estos agregados poseen una mayor energía libre que los iones solvatados aislados, y se disocian rápidamente. Ocasionalmente, sin embargo, uno de estos protocristalitos alcanza un tamaño crítico cuya estabilidad le permite permanecer intacto el tiempo suficiente para servir como una superficie (un “núcleo”) sobre la cual la deposición de iones adicionales puede conducir a una estabilidad aún mayor. En este punto, el proceso pasa de la nucleación a la etapa de crecimiento.
Los cálculos teóricos predicen que la nucleación a partir de una solución perfectamente homogénea es un proceso bastante improbable; la supersaturación de diez veces debería producir solo un núcleo por cm 3 por año. Por lo tanto, se cree que la mayor parte de la nucleación ocurre heterogéneamente en la superficie de alguna otra partícula, posiblemente una partícula de polvo. La eficiencia de este proceso depende críticamente de la naturaleza y condición de la superficie que da origen al núcleo.


