1.3: Manejo de números grandes y pequeños
- Page ID
- 76220
El Ejemplo 3 de Medidas, Cantidades y Factores de Unidad (opens in new window) ilustra una ocurrencia común en la ciencia: los resultados a menudo involucran números muy grandes o fracciones muy pequeñas. Estados Unidos utilizó 66 500 000 000 000 000 J (julios) de energía en 1971, y la masa de una molécula de agua es de 0.000 000 000 000 000 000 000 000 029 9 g Tales números son inconvenientes para escribir y difíciles de leer correctamente. (Hemos dividido los dígitos en grupos de tres para facilitar la localización del punto decimal. Se usan espacios en lugar de comas porque muchos países usan una coma para indicar el decimal).
Hay dos formas de manejar este problema. Podemos expresar una cantidad en unidades mayores o menores, como en el Ejemplo 4 de Medidas, Cantidades y Factores de Unidad (opens in new window), o podemos usar una mejor manera de escribir números pequeños y grandes. Este último enfoque involucra lo que se denomina notación científica o notación exponencial. La posición del punto decimal se indica con una potencia (o exponente) de 10. Por ejemplo,
\[138= 13.8\cdot 10= 1.38\cdot 10\cdot 10= 1.38\cdot 10^2 \nonumber \]
\[0.004\ 83= \frac{4.83}{10\cdot10\cdot10} = 4.83\cdot\frac{1}{10^3} = 4.83\cdot10^{-3} \nonumber \]
Un número con un exponente negativo es simplemente el recíproco de (uno dividido por) el mismo número con el exponente positivo equivalente. Por lo tanto, las fracciones decimales (números entre cero y uno) pueden expresarse usando potencias negativas de 10. Los números entre 1 y 10 no requieren parte exponencial, y los mayores de 10 involucran exponentes positivos. Por convención se elige la potencia de 10 para que haya un dígito a la izquierda del punto decimal en el número ordinario. Es decir, normalmente escribiríamos 5280 como 5.28 × 10 3 no como 0.528 × 10 4 o 52.8 × 10 2.
Para convertir un número de notación ordinaria a científica, cuente cuántos lugares se debe desplazar el punto decimal para llegar a un número entre 1 y 10. Si estos cambios están a la izquierda, el número era grande para empezar y multiplicamos por una gran potencia (es decir, positiva) de 10. Si el desplazamiento es hacia la derecha, se debe utilizar un poder recíproco (negativo) de 10.
Expresar en notación científica los siguientes números: a) 7563; (b) 0.0156.
Solución
a) En este caso el punto decimal deberá desplazarse a la izquierda tres lugares:

Por lo tanto utilizamos un exponente de +3:
\[7563= 7.563\cdot10^3 \nonumber \]
b) Al desplazar el punto decimal dos lugares a la derecha se obtiene un número entre 1 y 10:

Por lo tanto el exponente es —2:
\[0.0156= 1.56\cdot10^{-2} \nonumber \]
Cuando se trabaja con notación exponencial, a menudo es necesario sumar, restar, multiplicar o dividir números. Al multiplicar y dividir, hay que recordar que la multiplicación corresponde a la suma de exponentes, y la división a su resta.
Multiplicación:\(\text{10}^a\cdot\text{10}^b = \text{10}^{\small(a + b\small)}\)
División:\(\frac{10^a}{10^b} = 10^{(a - b)}\)
De ahí\((3.0\cdot10^5)\cdot(5.0\cdot10^3) = 15.0\cdot10^{(5+3)}= 15.0\cdot10^8= 1.50\cdot10^9\) y\(\frac{3.0\cdot10^5}{5.0\cdot10^3} =0.6\cdot10^{(5- 3)} = 0.6\cdot10^2= 6.0\cdot10\)
Evalúa lo siguiente, dando tu respuesta en notación exponencial correcta:
- \((3.89 \cdot 10^5) \cdot (1.09 \cdot 10^{-3}) \)
- \((6.41\cdot10^{-5}) \cdot(2.72 \cdot10^{-2})\)
- \(\frac{(5.0\cdot10^6)}{(3.98\cdot10^8)} \)
- \(\frac{(7.53\cdot10^{-3})}{(8.57\cdot10^{-5})} \)
Solución:
- \((3.89\cdot10^5)\cdot(1.09 \cdot10^{-3}) = 3.89\cdot1.09\cdot10^{5 + (-3)}= 4.24\cdot10^2 \)
- \((6.41\cdot10^{-5})\cdot(2.72 \cdot10^{-2})\)\(6.41\cdot2.72\cdot10^{-5 + (-2)}\)=\(17.43 \cdot10^{-7}\) =\(1.743 \cdot10^{-6}\)
- \(\frac{(5.0\cdot10^6)}{(3.98\cdot10^8)}= \frac{5.0}{3.98} \cdot10^{6-8}= 1.26\cdot10^{-2} \)
- \(\frac{(7.53\cdot10^{-3})}{(8.57\cdot10^{-5})} = \frac{7.53}{8.57}\cdot10^{-3 - (-5)} = 0.879\cdot10^2 = 8.79\cdot10^1 \)
La suma y resta requieren que todos los números se conviertan a la misma potencia de 10. (Esto corresponde a alinear los puntos decimales.)
Evalúa lo siguiente, dando tu respuesta en notación científica:
a)\((6.32\cdot10^2) – (1.83 \cdot10^\cdot{-1}) \)
b)\((3.72 \cdot10^4) + (1.63\cdot10^5) – (1.7 10^3) \)
Solución:
a) Primero convertir a la misma potencia de 10; luego sumar los números ordinarios.
\( \begin{align}&&6.32\cdot10^2&=& 632 \\&&–1.83\cdot10^{-1}&=& – 0.183 \\632 – 0.183&=& 631.817&=& 6.318 17\cdot10^2 \end{align}\)
b) Convertir todos los poderes de 10 a 10 4.
\( \begin{align}3.72\cdot10^4 &=& 3.72 \cdot10^4 &=& 3.72 × 10^4 \\1.63\cdot10^5&=& 1.63\cdot10 \cdot10^4&=& 16.3 \cdot10^4 \\–1.7 \cdot10^3&=& –1.7 \cdot10^{-1}\cdot10^4&=& – 0.17\cdot10^4 \\ (3.72\cdot10^4) + (16.3\cdot10^4) - (0.17 \cdot10^4)&=& 19.85 \cdot10^4&=& 1.985\cdot10^5\end{align} \)
La notación científica es cada vez más común cada día. Muchas calculadoras electrónicas de bolsillo lo utilizan para expresar números que de otro modo no encajarían en sus pantallas. Por ejemplo, una calculadora de ocho dígitos no pudo mostrar el número 6 800 000 000.El punto decimal permanecería fijo a la derecha, y el 6 y el 8 se “desbordarían” hacia el lado izquierdo. Dicho número a menudo se muestra como 6.8 09, lo que significa 6.8 × 10 9. Si usa una calculadora que no tiene notación científica, le recomendamos que exprese todos los números como potencias de 10 antes de hacer cualquier aritmética. Sigue las reglas de los dos últimos ejemplos, usando tu calculadora para hacer aritmética sobre los números ordinarios. Deberías poder sumar o restar los poderes de 10 en tu cabeza.
Las computadoras también son propensas a imprimir resultados en notación científica, y utilizan otra modificación menor. El número impreso 2.3074 E-07 significa 2.3074 × 10 —7 por ejemplo. En este caso la E indica que el número siguiente es un exponente de 10.
Demasiados dígitos
Nuevamente en referencia a nuestro experimento de contaminación atmosférica (opens in new window), podríamos expresar la masa de humo recolectada como 3.42 × 10 —2 g y el volumen del globo como 1.021 926 4 × 10 7 cm 3. Sin embargo, hay algo extraño en la segunda cantidad. Contiene un número que se copió directamente de la pantalla de una calculadora electrónica y tiene demasiados dígitos.
La fiabilidad de una cantidad derivada de una medición se indica habitualmente por el número de cifras significativas (o dígitos significativos) que contiene. Por ejemplo, los tres dígitos significativos en la cantidad 3.42 × 10 —2 g nos indican que se utilizó un saldo en el que podríamos distinguir 3.42 × 10 —2 g de 3.43 × 10 —2 g o 3.41 × 10 —2 g Podría haber alguna duda sobre el último dígito, pero los de la izquierda de la misma se toman como completamente confiables. Otra forma de indicar lo mismo es (3.42±0.01) × 10 —2 g Nuestra medición está en algún lugar entre 3.41 × 10 —2 g y 3.43 × 10 —2 g.
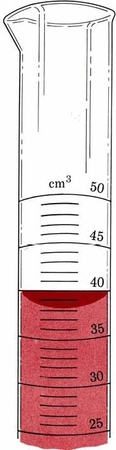
Como otro ejemplo de elegir un número apropiado de dígitos significativos, leamos el volumen de líquido en un cilindro graduado. El fondo del menisco se encuentra entre graduaciones correspondientes a 38 y 39 cm 3. Podemos estimar que está a 38.5 cm 3, pero el último dígito podría estar fuera un poco, quizás te parezca 38.4 o 38.6 cm 3. Dado que el tercer dígito está en cuestión, deberíamos usar tres cifras significativas. El volumen se registraría como 38.5 cm 3. El equipo de laboratorio a menudo se calibra de manera similar a este cilindro graduado; se debe estimar a la décima más cercana de la graduación más pequeña.
En algunos números ordinarios, por ejemplo, 0.001 23, los ceros sirven meramente para localizar el punto decimal. No indican la confiabilidad de la medición y por lo tanto no son significativas. Otra ventaja de la notación científica es que podemos suponer que todos los dígitos son significativos. Así, si 0.001 23 se escribe como 1.23 × 10 —3, solo se escriben los 1, 2 y 3, que indican la confiabilidad de la medición. El punto decimal se ubica por la potencia de 10.
Si se aplica la regla expresada en el párrafo anterior al volumen de aire recolectado en nuestro experimento de contaminación, 1.021 926 4 × 10 7 cm 3, encontramos que el volumen tiene ocho dígitos significativos. Esto implica que se determinó a ±1 cm 3 de aproximadamente 10 millones de cm 3, una confiabilidad que corresponde a ubicar a un saltamontes exactamente en algún punto de la carretera de Filadelfia a la ciudad de Nueva York. Para experimentos tan crudos como el nuestro, esto no es probable. Veamos qué tan buena fue la medición.
Recordará que calculamos el volumen a partir del diámetro del globo (se abre en una ventana nueva), 106 pulg. Las tres cifras significativas implican que esto podría haber sido tan grande como 107 pulgadas o tan pequeño como 105 pulgadas. Podemos repetir el cálculo con cada una de estas cantidades para ver qué tan lejos estaría el volumen:
\[\begin{equation} \begin{split} r &= \frac{1}{2} \times \text{107 in} = \text{53.5 in} \times \frac{\text{1 cm}}{\text{0.3937 in}} \\ \\ &=135.890 27 \text{cm} \end{split} \end{equation} \nonumber \]
\[\begin{align} V &= \frac{4}{3} \times 3.141 59 \times (135.890 27)^3 \\ \\ &= 10 511 225 \text{cm}^3 = 1.051 122 5 \times 10^7 \text{cm}^3 \end{align} \nonumber \]
o
\[\begin{align} V &= \frac{4}{3} \times 3.14159 \times \left( \frac{1}{2} \times \text{105 in} \frac{\text{1 cm}}{\text{0.3937 in}}\right)^3 \\ \\ &= 9 932 759 \text{cm}^3 = 0.993 275 9 \times 10^7 \text{cm}^3 \end{align} \nonumber \]
Es decir, el volumen está entre 0.99 × 10 7 y 1.05 × 10 7 cm 3 o (1.02 ± 0.03) × 10 7 cm 3. Deberíamos redondear nuestro resultado a tres cifras significativas, por ejemplo, 1.02 cm³, porque el último dígito, es decir, 2, está en duda.
- Todos los dígitos a redondear se eliminan juntos, no uno a la vez.
- Si el dígito más a la izquierda a eliminar es menor de cinco, el último dígito retenido no se altera.
- Si el dígito más a la izquierda a eliminar es mayor que cinco, el último dígito retenido se incrementa en uno.
- Si el dígito más a la izquierda a eliminar es cinco y al menos uno de los otros dígitos a eliminar no es cero. el último dígito retenido se incrementa en uno.
- Si el dígito que más a la izquierda le quitó es cinco y todos los demás dígitos a eliminar son cero, el último dígito retenido no se altera si es par, sino que se incrementa en uno si es impar.
La aplicación de las Reglas para Redondear Números se puede ilustrar con un ejemplo.
Redondear cada uno de los números a continuación a tres cifras significativas.
- 34.7449
- 34.864
- 34.754
- 34.250
- 34.35
Solución:
a) Aplicar las reglas 1 y 2:
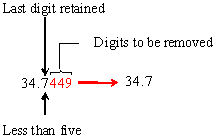
(Tenga en cuenta que se obtendría un resultado diferente si los dígitos se redondearan incorrectamente uno a la vez desde la derecha).
b) Aplicar reglas 1 y 3:34.8 64 → 34.9
c) Aplicar reglas 1 y 4:34.7 54 → 34.8
d) Aplicar reglas 1 y 5:34.2 50 → 34.2
e) Aplicar regla 5:34.3 5 → 34.4
¿A cuántas cifras significativas debemos redondear nuestros resultados de contaminación del aire? Ya hemos hecho un cálculo que implica multiplicación y división para obtener el volumen de nuestro globo de captación de gas. Se trata de los siguientes números:
| 106 | Tres cifras significativas |
|---|---|
| 0.3937 | Cuatro cifras significativas |
| 3.141 59 | Seis cifras significativas (podríamos obtener más si quisiéramos) |
|
\(\frac{4}{3}\)y\(\frac{1}{2}\) |
Un número infinito de cifras significativas ya que los enteros en estas fracciones son exactos por definición. No se consideran números exactos o 'definidos' al calcular cifras significativas. |
El resultado del cálculo contenía tres cifras significativas, las mismas que el número menos confiable. Esto ilustra la regla general de que para la multiplicación y división el número de cifras significativas en el resultado es el mismo que en la medición menos confiable. Se supone que números definidos como π, ½ o 100 cm/1m tienen un número infinito de cifras significativas.
En el caso de suma y resta, se aplica una regla diferente. Supongamos, por ejemplo, que pesamos un filtro de recolección de humo en una balanza relativamente inexacta que solo podría leerse al 0.01 g más cercano. Después de recolectar una muestra, el filtro se volvió a pesar en una balanza de una sola sartén para determinar la masa de partículas de humo.
Masa final: 2.374 5 g (los dígitos coloreados están en cuestión)
Masa inicial: —2.3 2 g
Masa de humo: 0.0 545 g
Dado que el pesaje inicial podría haber sido de 2.31 a 2.33 g, las tres cifras del resultado final están en duda. (Debe estar entre 0.0445 y 0.0645 g). Por lo tanto, no hay más que un dígito significativo, y el resultado es de 0.05g. La regla aquí es que el resultado de suma o resta no puede contener más dígitos a la derecha de los que hay en ninguno de los números sumados o restados. Tenga en cuenta que la resta puede reducir drásticamente el número de dígitos significativos cuando se aplica esta regla.
Redondear números es especialmente importante si se utiliza una calculadora electrónica, ya que estas máquinas suelen mostrar una gran cantidad de dígitos, la mayoría de los cuales carecen de sentido. El mejor procedimiento es llevar todos los dígitos hasta el final del cálculo (¡a tu calculadora no le importará el trabajo extra!) y luego redondear apropiadamente. Las respuestas a los cálculos posteriores en este libro se redondearán de acuerdo con las reglas dadas. Es posible que desee volver a los ejemplos anteriores y redondear sus respuestas correctamente también.
Evaluar las siguientes expresiones, redondeando la respuesta al número apropiado de cifras significativas.
- \( \text{32.61 g} + \text{8.446 g} + \text{7.0 g} \)
- \( \text{0.136 cm}^3 \times \text{10.685 g cm}^{-3} \)
Solución
- \(\text{32.61 g} + \text{8.446 g} + \text{7.0 g} = \text{48.056 g} = \text{48.1g (7.0 has only one figure to the right of the decimal point.)} \)
- \( 0.136 \text{cm}^3 \times 10.685 \text{g cm}^{-3} = \text{1.453 g} = \text{1.45g (0.136 has only three significant figures.)} \)
Cuando sugerimos llenar un globo meteorológico excedente para medir la cantidad de gas que se bombeó a través de nuestro colector de contaminación del aire, mencionamos que esta sería una forma bastante cruda de determinar el volumen. Por un lado, no sería tan sencillo medir el diámetro de una esfera de 8 o 9 pies de manera confiable. Usando una vara de medir, tendríamos la suerte de tener medidas sucesivas acordadas dentro de media pulgada más o menos. Fue por esta razón que el resultado se reportó a la pulgada más cercana. El grado en que las mediciones repetidas de la misma cantidad dan el mismo resultado se denomina precisión. La repetición de una medición altamente precisa produciría resultados casi idénticos, mientras que la baja precisión implica que los números diferirían en un porcentaje significativo entre sí.
Se podría lograr una medición muy precisa del diámetro de nuestro globo, pero probablemente no valdría la pena. Hemos asumido una forma esférica, pero es casi seguro que esto no es exactamente correcto. No importa cuán precisamente determinemos el diámetro, nuestra medición del volumen de gas estará influenciada por desviaciones de la forma asumida. Cuando uno o más de nuestros supuestos sobre un instrumento de medición son erróneos, la precisión de un resultado se verá afectada. Un ejemplo obvio sería una regla de pie dividida en 11 pulgadas iguales. Las mediciones que emplean este instrumento podrían estar de acuerdo con mucha precisión, pero no serían muy precisas.
Un punto importante de otro tipo se ilustra en los dos últimos párrafos. Se han adoptado muchas palabras comunes en el lenguaje de la ciencia. Por lo general, tal adopción va acompañada de una definición científica inequívoca que no aparece en un diccionario normal. La precisión y la precisión se tratan muchas veces como sinónimos, pero en la ciencia cada uno tiene un significado ligeramente diferente. Otro ejemplo es la cantidad, que hemos definido en términos de “número × unidad”. Otras palabras en inglés como bulto, tamaño, cantidad, etc., pueden ser sinónimos de cantidad en el habla cotidiana, pero no en la ciencia. A medida que te encuentres con otras palabras como esta, trata de aprender y usar la definición científica lo antes posible, y evita confundirla con los otros significados que ya conoces.
Incluso otorgando la crudeza de las mediciones que acabamos de describir, serían adecuadas para demostrar si existía o no un problema de contaminación del aire. El siguiente paso sería encontrar un químico o funcionario de salud pública que fuera experto en evaluar la calidad del aire, presentar sus datos y convencer a esa persona de que preste su habilidad y autoridad a su argumento de que algo andaba mal. Dicha persona tendría a su disposición equipo cuya precisión y exactitud fueran adecuadas para mediciones altamente confiables y podría hacer declaraciones públicas autorizadas sobre la magnitud del problema de la contaminación del aire.
Fuentes Web
Varios sitios se inspiraron en “Poderes de diez” Poderes de diez de Charles Eames™ (1977) (opens in new window) [www.powersof10.com (opens in new window)]: Word Wizz (opens in new window) [www.wordwizz.com] Secret Worlds: The Universe Within (opens in new window) ventana) [micro.magnet.fsu.edu]


