1.6: Medidas, cantidades y factores de unidad
- Page ID
- 76199
Mediciones
Supongamos que se enfrenta a un problema específico. Entonces podemos ver cómo el pensamiento científico podría ayudar a resolverlo. Supongamos que vive cerca de una planta grande que fabrica cemento. El humo de la planta se asienta en tu auto y casa, provocando pequeños pozos en la pintura. A usted le gustaría detener este problema de contaminación del aire, pero ¿cómo?
Como individuo probablemente tendrá poca influencia, e incluso como parte de un grupo de ciudadanos preocupados puede ser ineficaz, a menos que pueda demostrar que existe un problema. Los científicos han participado en la redacción de la mayoría de las regulaciones de contaminación del aire, por lo que tendrás que emplear algunas técnicas científicas (o un científico) para ayudar a resolver tu problema.
Probablemente será necesario determinar cuánta contaminación del aire está produciendo la planta. Esto podría hacerse comparando el humo con una escala que va del blanco al gris al negro, suponiendo que cuanto más oscuro es el humo, más hay. Para el polvo de cemento blanco, sin embargo, esto es mucho menos satisfactorio que para el humo de carbón negro. Una mejor manera de determinar cuánta contaminación hay sería medir la masa de partículas de humo que podrían recolectarse cerca de su casa o automóvil. Esto podría hacerse usando una bomba (como una aspiradora) para aspirar el gas contaminado a través de un filtro. Pesar el filtro antes y después de dicho experimento determinaría qué masa de humo se había recolectado.
Masa y peso
Debido a que el peso es la fuerza de gravedad sobre un objeto, que varía de un lugar a otro en aproximadamente 0.5% como se muestra en la Tabla, debemos usar la masa para mediciones precisas de cuánta materia tenemos. Todavía llamamos “pesaje” al proceso de obtención de una masa precisa.
| Latitud, o | Altitud = 0 | Altitud = 10 km |
|---|---|---|
| 0 | 9.78036 | 9.74950 |
| 30 | 9.79324 | 9.76238 |
| 60 | 9.81911 | 9.78825 |
| 90 | 9.83208 | 9.80122 |
El peso de un objeto es en realidad la fuerza de la gravedad, y se calcula como
\[F=\text{“W”}=m \times g \label{1} \]
El peso se mide en newtons (kg m s -2) o libras (lb), donde 1 lb = 4.44822162 newtons. La unidad base para masa es kilogramos (kg), pero la libra también puede ser utilizada como unidad de masa (1 libra = 0.45359237 kilogramos). El valor promedio de g generalmente se toma como 9.80665 m s -2, por lo que el peso de una masa de 1 kg sería
\[F = \text{ “W” } = m \times g = 1 \text{ kg} \times 9.80665 \text{ m s}^{-2} = 9.80665 \text{ N or } 2.2046 \text{ lb} \nonumber \]
Si el peso de la masa de 1 kg se midiera en un campamento de exploración ártica con una balanza de célula de carga (ver abajo) aún calibrada para el g promedio, su peso sería:
\[ F = \text{ “W” } = m \times g = 10 \text{ kg} \times 9.83208 \text{ m s}^{-2} = 9.83208 \text{ N or } 2.2103 \text{ lb} \nonumber \]
El pesaje preciso generalmente se realiza con una sola balanza de sartén. La sartén vacía se equilibra con un contrapeso. Cuando se coloca un objeto en la sartén, la atracción gravitacional obliga a la cacerola hacia abajo. Para restablecer el equilibrio, se retiran una serie de pesos (objetos de masa conocida) de los soportes por encima de la sartén. La fuerza de atracción gravitacional es proporcional a la masa, y cuando la sartén está equilibrada, la fuerza sobre ella debe ser siempre la misma. Por lo tanto, la masa del objeto que se está pesando debe ser igual a la de los pesos que fueron retirados. Una balanza da la misma lectura de masa independientemente de la fuerza de gravedad.

Las “balanzas” modernas de laboratorio se basan en celdas de carga que convierten la fuerza ejercida por un objeto sobre el balancín en una señal eléctrica. La celda de carga generalmente se acopla con un convertidor dedicado y una pantalla digital. Debido a que la fuerza ejercida por el objeto depende de la gravedad, estas son realmente escalas que miden el peso, y deben ser calibradas frecuentemente (contra masas estándar) para leer una masa.
Mediciones de Masa
Si llevabas un cuaderno u otro registro de tus medidas, probablemente escribirías algo así como 0.0342 g para representar la cantidad de humo que se había recolectado. Tal resultado, que describe la magnitud de algún parámetro (en este caso la magnitud del parámetro, masa), se denomina cantidad. Observe que consta de dos partes, un número y una unidad. Sería ambiguo escribir solo 0.0342, quizás no recuerdes más tarde si eso se midió en unidades de gramos, onzas, libras o algo más. Una cantidad siempre se comporta como si el número y las unidades se multiplicaran juntas. Por ejemplo, podríamos escribir la cantidad ya obtenida como 0.0342 × g. Usando esta simple regla de número × unidades, podemos aplicar aritmética y álgebra a cualquier cantidad:
\[\begin{align} & 5 \text{g} + 2 \text{g} = (5 + 2) \text{g} = 7 \text{g} \\ & 5 \text{g} \div 2 \text{g} = \dfrac{5 \text{g}}{2 \text{g}} = 2.5 \text{ (the units cancel, and so we get a pure number)} \\ & 5 \text{ in} \times 2 \text{ in} = 10 \text{ in}^{2} \text{ (10 square inches)}\end{align} \nonumber \]
Esto funciona perfectamente siempre y cuando no escribamos ecuaciones con diferentes parámetros (es decir, aquellos que tienen unidades que miden diferentes propiedades, como masa y longitud, temperatura y energía, o volumen y cantidad) en lados opuestos del signo igual. Por ejemplo, aplicar álgebra a la ecuación
\[ 5 \text{g} = 2 \text{ in}^{2} \nonumber \]
puede generar problemas de la misma manera que dividir por cero lo hace y debe evitarse, porque gramos (g) es una unidad de la masa del parámetro, y la pulgada (in) es una unidad de la longitud del parámetro.
Conversiones con Factores de Unidad
Factores de unidad de masa
Observe también que si una cantidad es grande o pequeña depende del tamaño de las unidades así como del tamaño del número. Por ejemplo, la masa de humo se ha medido como 0.0342 g, pero el saldo podría haberse ajustado para que se lea en miligramos (o granos en el sistema inglés). Entonces la lectura sería de 34.2 mg (o 0.527 granos). Los resultados (0.0342 g, 34.2 mg, o 0.527 gr) son la misma cantidad, la masa de humo. Uno involucra un número menor y una unidad más grande (0.0342 g), mientras que los otros tienen un número mayor y una unidad más pequeña. Siempre y cuando estemos hablando de la misma cantidad, es una cuestión sencilla ajustar el número para ir con las unidades que queramos.
Podemos convertir entre las diferentes formas de expresar la masa con factores de unidad de la siguiente manera:
Como 1 mg y 0.001 g son el mismo parámetro (masa), podemos escribir la ecuación
\[ 1 \text{ mg} = 0.001 \text{ g} \nonumber \]
Dividiendo ambos lados por 1 mg, tenemos
\[1 = \dfrac{1\text{ mg}}{1\text{ mg}} = \dfrac{0.001\text{ g}}{1\text{ mg}} \nonumber \]
Dado que el último término de esta ecuación es igual a uno, se le llama factor de unidad. Se puede multiplicar por cualquier cantidad, dejando la cantidad sin cambios.
Podemos generar otro factor de unidad dividiendo ambos lados por 0.001 g:
\[1 = \dfrac{1\text{ mg}}{0.001\text{ g}} = \dfrac{0.001\text{ g}}{0.001\text{ g}} \nonumber \]
¿Cuál es la masa en gramos de una tableta de aspirina de 5.0 granos (5 gr), dado que 1 gram = 15.4323584 granos?
Solución:
\[ 5.0 \text{ gr} = 5.0 \text{ gr} \times 1 = 5.0 \text{ gr}\times \dfrac{1.0\text{ g}}{\text{15.4323 gr}} \nonumber \]
Las unidades gr cancelan, dando el resultado
\[ 5.0 \text{ gr} = 5.0 \div 15.4323 \text{ g} = 0.324 \text{ g} \nonumber \]
Factores de unidad de longitud
La longitud del parámetro puede medirse en pulgadas (in) en el sistema inglés, pero las mediciones científicas (todas las mediciones en el mundo excluyentes de EE. UU.) se reportan en las unidades métricas de metros (m) o alguna unidad derivada más conveniente como centímetros (cm).
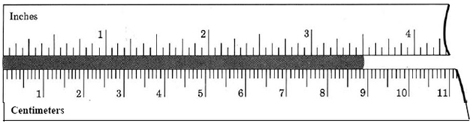
Expresa la longitud 8.89 cm en pulgadas, dado que 1 cm = 0.3937 in.
Solución
Dado que 1 cm y 0.3937 pulgadas son la misma cantidad, podemos escribir la ecuación
\[1 \text{ cm} = 0.3937 \text{ in} \nonumber \]
Dividiendo ambos lados por 1 cm, tenemos
\[1 = \dfrac{0.3937\text{ in}}{1\text{ cm}} \nonumber \]
Dado que el lado derecho de esta ecuación es igual a uno, se le llama factor de unidad. Se puede multiplicar por cualquier cantidad, dejando la cantidad sin cambios.
\[ 8.89 \text{ cm} = 8.89 \text{ cm} \times 1 = 8.89 \text{ cm} \times \dfrac{0.3937\text{ in}}{\text{1 cm}} \nonumber \]
Las unidades centímetros cancelan, arrojando el resultado 8.89 cm = 8.89 × 0.3937 in = 3.50 in
Esto concuerda con la observación directa que se hace en la figura.
Veamos nuestro problema de contaminación del aire. Probablemente ya se te haya ocurrido que simplemente medir la masa de humo recolectada no es suficiente. Algunas otras variables pueden afectar su experimento y también deben medirse si los resultados van a ser reproducibles. Por ejemplo, la dirección y velocidad del viento casi con certeza serían importantes. También debe anotarse la hora del día y la fecha en que se realizó una medición. Además probablemente deberías especificar qué tipo de filtro estás usando. Algunos no son lo suficientemente finos como para atrapar todas las partículas de humo.
Temperatura
Otra variable que casi siempre se registra es la temperatura. Un termómetro es fácil de usar, y la temperatura puede variar mucho al aire libre, donde tendrían que hacerse sus experimentos.
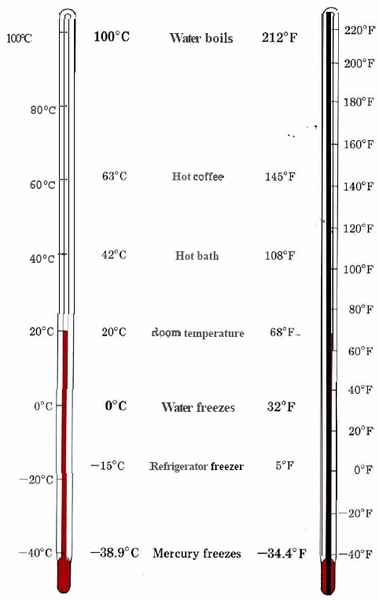

En el trabajo científico, las temperaturas generalmente se reportan en grados Celsius (°C), una escala en la que el punto de congelación del agua pura es de 0°C y el punto de ebullición normal de 100°C En Estados Unidos, sin embargo, sería más probable tener disponible un termómetro calibrado en grados Fahrenheit (°F). La relación entre estas dos escalas de temperatura es
\[\dfrac{\text{T}_{(^{o}\text{F)}} - 32}{\text{T}_{(^{o}\text{C)}}}=\dfrac{9}{5} \nonumber \]
Tenga en cuenta que las escalas de temperatura no se pueden interconvertir con factores de unidad simples, ya que no tienen un punto cero común (0°C = 32°F). Más bien, se debe utilizar la función matemática anterior. La ecuación anterior se escribe en términos del parámetro temperatura (T) con las unidades o dimensiones subinscritas entre paréntesis.
Mediciones de Volumen
Más importante que cualquiera de las variables anteriores es el hecho de que cuanto más aire bombee a través del filtro, más humo recogerá. Dado que el aire es un gas, es más fácil medir cuánto recolectas en términos de volumen que en términos de masa, y así podrías decidir hacerlo de esa manera. Hacer funcionar su bomba hasta que haya llenado un globo meteorológico de plástico proporcionaría una medición de volumen cruda y económica. Suponiendo que el globo sea aproximadamente esférico, podría medir su diámetro y calcular su volumen a partir de la fórmula
\[V=\dfrac{4}{3}\pi r^{3} \nonumber \]
Calcular el volumen de gas en una esfera cuyo diámetro es de 106 pulg. Expresa tu resultado en centímetros cúbicos (cm 3).
Solución
Dado que el radio de una esfera es la mitad de su diámetro,
\[ r = \dfrac{1}{2} \times 106 \text{ in} = 53 \text{ in} \nonumber \]
Podemos usar la misma igualdad de cantidades que en el Ejemplo 1 para convertir el radio a centímetros. Cuando cubicemos el número y las unidades, nuestro resultado será en centímetros cúbicos.
\[ 1 \text{ cm} = 0.3937 \text{ in} \nonumber \]
\[\dfrac{\text{1 cm}}{\text{0}\text{.3937 in}} = 1 \nonumber \]
\[ R = 53 \text{ in} \times \dfrac{\text{1 cm}}{\text{0}\text{.3937 in}} = \dfrac{\text{53}}{\text{0}\text{.3937}} \text{ cm} \nonumber \]
Usando la fórmula
\[\begin{align} & V =\dfrac{\text{4}}{\text{3}}\pi r^{\text{3}}=\dfrac{\text{4}}{\text{3}}\times \text{3}\text{.14159}\times ( \dfrac{\text{53}}{\text{0}\text{.3937}}\text{cm} )^{3} \\ & \text{ }=\text{10219264 cm}^{\text{3}} \\ & \end{align} \nonumber \]
Se puede ver en los Ejemplos 1 y 2 que se pueden obtener dos factores de unidad de la igualdad
\[ 1 \text{ cm} = 0.3937 \text{ in} \nonumber \]
Podemos usar uno de ellos para convertir pulgadas a centímetros y el otro para convertir centímetros a pulgadas. El factor correcto es siempre el que resulta en la cancelación de las unidades que no queremos.
El resultado del Ejemplo 2 también muestra que los centímetros cúbicos son unidades bastante pequeñas para expresar el volumen del globo. Si usáramos unidades más grandes, como se muestra en el siguiente ejemplo, no necesitaríamos más de 10 millones de ellas para reportar nuestra respuesta.
Expresar el resultado del Ejemplo 3 en metros cúbicos, dado que 1 m = 100 cm.
Solución
Nuevamente deseamos usar un factor de unidad, y como estamos tratando de deshacernos de los centímetros cúbicos, los centímetros deben estar en el denominador:
\[\text{1 = }\dfrac{\text{1 m}}{\text{100 cm}} \nonumber \]
Pero esto no permitirá la cancelación de centímetros cúbicos. No obstante, tenga en cuenta que 1 3 = 1 Es decir, podemos elevar un factor de unidad a cualquier poder, y sigue siendo unidad. Por lo tanto
\[\begin{align} & \text{1 =}\left( \text{ }\dfrac{\text{1 m}}{\text{100 cm}} \right)^{\text{3}}\text{ = }\dfrac{\text{1 m}^{\text{3}}}{\text{100}^{\text{3}}\text{ cm}^{\text{3}}}\text{ = }\dfrac{\text{1 m}^{\text{3}}}{\text{1 000 000 cm}^{\text{3}}} \\ \text{ and } \\ & \text{10 219 264 cm}^{\text{3}}\text{ = 10 219 264 cm}^{\text{3}}\text{ }\times \text{ }\left( \dfrac{\text{1 m}}{\text{100 cm}} \right)^{\text{3}} \\ & \text{ = 10 219 264 cm}^{\text{3}}\text{ }\times \text{ }\dfrac{\text{1 m}^{\text{3}}}{\text{100 000 cm}^{\text{3}}} \\ & \text{ = 10.219 264 m}^{\text{3}} \\ & \end{align} \nonumber \]


