Saltar al contenido principal
LibreTexts Español

12.1: Espontaneidad

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    77651

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Habilidades para Desarrollar

    • Distinguir entre procesos espontáneos y no espontáneos
    • Describir la dispersión de materia y energía que acompaña a ciertos procesos espontáneos

    En esta sección, considere las diferencias entre dos tipos de cambios en un sistema: Los que ocurren espontáneamente y los que ocurren por la fuerza. Al hacerlo, entenderemos por qué algunos sistemas están naturalmente inclinados a cambiar en una dirección bajo ciertas condiciones y cuán relativamente rápido o lento procede ese cambio natural. También obtendremos una idea de cómo la espontaneidad de un proceso afecta la distribución de energía y materia dentro del sistema.

    Procesos espontáneos y no espontáneos

    Los procesos tienen una tendencia natural a ocurrir en una dirección bajo un conjunto dado de condiciones. El agua fluirá naturalmente cuesta abajo, pero el flujo cuesta arriba requiere una intervención externa como el uso de una bomba. El hierro expuesto a la atmósfera terrestre se corroerá, pero el óxido no se convierte en hierro sin un tratamiento químico intencional. Un proceso espontáneo es aquel que ocurre naturalmente bajo ciertas condiciones. Un proceso no espontáneo, por otro lado, no se llevará a cabo a menos que sea “impulsado” por la entrada continua de energía de una fuente externa. Un proceso que es espontáneo en una dirección bajo un conjunto particular de condiciones no es espontáneo en la dirección inversa. A temperatura ambiente y presión atmosférica típica, por ejemplo, el hielo se derretirá espontáneamente, pero el agua no se congelará espontáneamente.

    La espontaneidad de un proceso no se correlaciona con la velocidad del proceso. Un cambio espontáneo puede ser tan rápido que es esencialmente instantáneo o tan lento que no se puede observar en ningún período práctico de tiempo. Para ilustrar este concepto, considere la desintegración de los isótopos radiactivos, un tema tratado más a fondo en el capítulo sobre química nuclear. La desintegración radiactiva es por definición un proceso espontáneo en el que los núcleos de los isótopos inestables emiten radiación a medida que se convierten en núcleos más estables. Todos los procesos de descomposición ocurren espontáneamente, pero las tasas a las que los diferentes isótopos se descomponen varían ampliamente. El tecnecio-99m es un radioisótopo popular para estudios de imágenes médicas que experimenta una descomposición relativamente rápida y exhibe una vida media de aproximadamente seis horas. El uranio-238 es el isótopo más abundante del uranio, y su desintegración ocurre mucho más lentamente, exhibiendo una vida media de más de cuatro mil millones de años (Figura\(\PageIndex{1}\)).

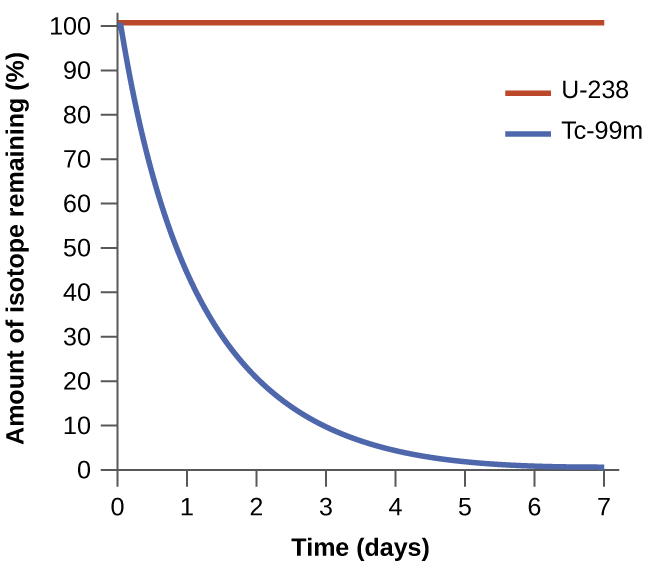
    Se muestra una gráfica de dos líneas donde se etiqueta el eje y, “cantidad de isótopo restante (signo porcentual)”, y tiene valores de cero a cien, en incrementos de diez, escritos a lo largo del eje. El eje x está etiquetado, “tiempo (días)” y tiene valores de cero a siete, en incrementos de uno, escritos a lo largo del eje. El primer gráfico, dibujado con una línea azul, comienza en el valor superior izquierdo de cien en el eje y y cero en el eje x y cae abruptamente durante los primeros tres minutos, luego la línea gráfica se vuelve casi horizontal hasta que alcanza los siete minutos en el eje x. La segunda gráfica, dibujada en rojo, comienza en el mismo punto que la primera, pero permanece perfectamente horizontal sin cambios a lo largo del eje y. Una leyenda etiqueta la línea roja como, “U dash 238”, y la línea azul como,
    Figura\(\PageIndex{1}\): Tanto el U-238 como el Tc-99m experimentan desintegración radiactiva espontánea, pero a velocidades drásticamente diferentes. En el transcurso de una semana, esencialmente toda una muestra de Tc-99m y ninguna de una muestra U-238 habrán decaído.

    Como otro ejemplo, considere la conversión del diamante en grafito (Figura\(\PageIndex{2}\)).

    \[\ce{C}_{(s,\textrm{ diamond})}⟶\ce{C}_{(s,\textrm{ graphite})} \label{Eq1}\]

    El diagrama de fases para el carbono indica que el grafito es la forma estable de este elemento bajo presión atmosférica ambiente, mientras que el diamante es el alótropo estable a presiones muy altas, como las presentes durante su formación geológica. Los cálculos termodinámicos del tipo descrito en la última sección de este capítulo indican que la conversión del diamante en grafito a presión ambiente ocurre espontáneamente, sin embargo, se observa que los diamantes existen, y persisten, bajo estas condiciones. Aunque el proceso es espontáneo en condiciones ambientales típicas, su velocidad es extremadamente lenta, por lo que para todos los fines prácticos los diamantes son de hecho “para siempre”. Situaciones como estas enfatizan la importante distinción entre los aspectos termodinámicos y cinéticos de un proceso. En este caso particular, se dice que los diamantes son termodinámicamente inestables pero cinéticamente estables en condiciones ambientales.

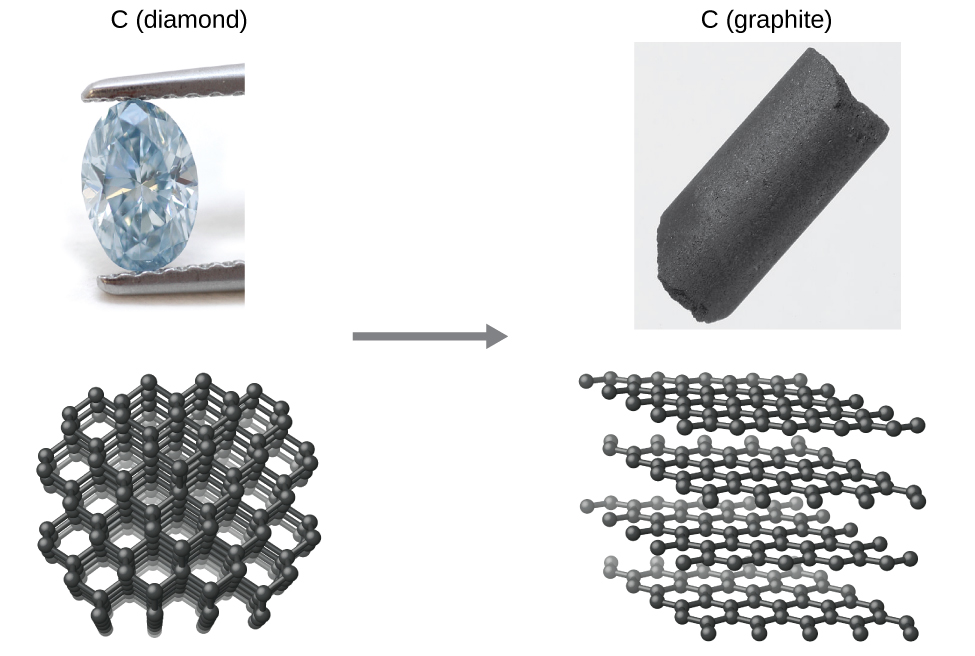
    Se muestran dos pares de imágenes. El par izquierdo, etiquetado, “C, (diamante)”, tiene una imagen de un diamante sostenido por un par de plyers y un diagrama de la disposición molecular. El segundo par, etiquetado como “C (grafito)”, tiene una imagen de una roca grande, negra, ligeramente brillante y un diagrama de cuatro láminas compuestas por muchos átomos dispuestos en grandes cuadrados en una disposición apilada con espacio entre cada una.

    Figura\(\PageIndex{2}\):The conversion of carbon from the diamond allotrope to the graphite allotrope is spontaneous at ambient pressure, but its rate is immeasurably slow at low to moderate temperatures. This process is known as graphitization, and its rate can be increased to easily measurable values at temperatures in the 1000–2000 K range. (credit "diamond" photo: modification of work by "Fancy Diamonds"/Flickr; credit "graphite" photo: modificaton of work by images-of-elements.com/carbon.php)

    Dispersal of Matter and Energy

    As we extend our discussion of thermodynamic concepts toward the objective of predicting spontaneity, consider now an isolated system consisting of two flasks connected with a closed valve. Initially there is an ideal gas on the left and a vacuum on the right (Figure \(\PageIndex{3}\)). When the valve is opened, the gas spontaneously expands to fill both flasks. Recalling the definition of pressure-volume work from the chapter on thermochemistry, note that no work has been done because the pressure in a vacuum is zero.

    \[w=−PΔV=0 \;\;\; \mathrm{(P=0\: in\: a\: vaccum)} \label{Eq2}\]

    Note as well that since the system is isolated, no heat has been exchanged with the surroundings (q = 0). The first law of thermodynamics confirms that there has been no change in the system’s internal energy as a result of this process.

    \[ΔU=q+w=0+0=0 \label{Eq3}\]

    The spontaneity of this process is therefore not a consequence of any change in energy that accompanies the process. Instead, the driving force appears to be related to the greater, more uniform dispersal of matter that results when the gas is allowed to expand. Initially, the system was comprised of one flask containing matter and another flask containing nothing. After the spontaneous process took place, the matter was distributed both more widely (occupying twice its original volume) and more uniformly (present in equal amounts in each flask).

    A diagram shows two two-sided flasks connected by a right-facing arrow labeled “Spontaneous” and a left-facing arrow labeled “Nonspontaneous.” Each pair of flasks are connected to one another by a tube with a stopcock. In the left pair of flasks, the left flask contains thirty particles evenly dispersed while the right flask contains nothing and the stopcock is closed. The right pair of flasks has an open stopcock and equal numbers of particles in both flasks.

    Figura\(\PageIndex{3}\):An isolated system consists of an ideal gas in one flask that is connected by a closed valve to a second flask containing a vacuum. Once the valve is opened, the gas spontaneously becomes evenly distributed between the flasks.

    Now consider two objects at different temperatures: object X at temperature TX and object Y at temperature TY, with TX > TY (Figure \(\PageIndex{4}\)). When these objects come into contact, heat spontaneously flows from the hotter object (X) to the colder one (Y). This corresponds to a loss of thermal energy by X and a gain of thermal energy by Y.

    \[q_\ce{X}<0 \hspace{20px} \ce{and} \hspace{20px} q_\ce{Y}=−q_\ce{X}>0 \label{Eq4}\]

    From the perspective of this two-object system, there was no net gain or loss of thermal energy, rather the available thermal energy was redistributed among the two objects. This spontaneous process resulted in a more uniform dispersal of energy.

    Two diagrams are shown. The left diagram is comprised of two separated squares; the left is red and labeled “X” and the right is blue and labeled “Y.” Below this diagram is the label “T subscript X, a greater than sign, T subscript Y.” The right diagram shows the boxes next to one another, shaded red on the left, blue on the right, and blended red and blue together in the middle. The left box is red and labeled “X,” the right is blue and labeled “Y” and a right-facing arrow labeled “Heat” is written above them. Below this diagram is the label “X and Y in contact.

    Figura:Cuando\(\PageIndex{4}\) dos objetos a diferentes temperaturas entran en contacto, el calor fluye espontáneamente del objeto más caliente al más frío.

    Como lo ilustran los dos procesos descritos, un factor importante para determinar la espontaneidad de un proceso es la medida en que cambia la dispersión o distribución de materia y/o energía. En cada caso, se produjo un proceso espontáneo que resultó en una distribución más uniforme de la materia o energía.

    Ejemplo\(\PageIndex{1}\): Redistribución de la materia durante un proceso espontáneo

    Describir cómo se redistribuye la materia cuando se llevan a cabo los siguientes procesos espontáneos:

    1. Un sólido sublima.
    2. Un gas se condensa.
    3. Una gota de colorante alimentario añadida a un vaso de agua forma una solución con color uniforme.

    Solución

    Esta figura tiene tres fotos etiquetadas, “a”, “b” y “c”. La foto a muestra un vaso con un sólido en agua. Hay vapor o humo que viene de la parte superior del vaso. La foto b muestra la mitad inferior de un vaso con agua pegada a su superficie exterior. La foto c muestra un recipiente sellado que contiene un líquido rojo.

    Figura\(\PageIndex{5}\) :( crédito a: modificación de obra de Jenny Downing; crédito b: modificación de obra por “Fuzzy Gerdes” /Flickr; crédito c: modificación de obra de Sahar Atwa)

    1. a) La sublimación es la conversión de un sólido (densidad relativamente alta) a gas (densidad mucho menor). Este proceso produce una dispersión mucho mayor de la materia, ya que las moléculas ocuparán un volumen mucho mayor después de la transición sólido-gas.
    2. (b) La condensación es la conversión de un gas (densidad relativamente baja) a líquido (densidad mucho mayor). Este proceso produce una dispersión mucho menor de la materia, ya que las moléculas ocuparán un volumen mucho menor después de la transición sólido-gas.
    3. c) El proceso en cuestión es la dilución. Las moléculas de colorante alimentario inicialmente ocupan un volumen mucho menor (la gota de solución de tinte) de lo que ocupan una vez que se completa el proceso (en el vaso lleno de agua). Por lo tanto, el proceso conlleva una mayor dispersión de la materia. El proceso también puede producir una dispersión más uniforme de la materia, ya que el estado inicial del sistema involucra dos regiones de diferentes concentraciones de colorante (alta en la caída, cero en el agua), y el estado final del sistema contiene una sola concentración de colorante en todo el proceso.

    Ejercicio\(\PageIndex{1}\)

    Describa cómo se redistribuye la materia y/o la energía cuando vacía un bote de aire comprimido en una habitación.

    Respuesta:

    Este es también un proceso de dilución, análogo al ejemplo (c). Implica tanto una dispersión mayor como más uniforme de la materia ya que se permite que el aire comprimido en el bote se expanda hacia el aire de menor presión de la habitación.

    Resumen

    Los procesos químicos y físicos tienen una tendencia natural a ocurrir en una dirección bajo ciertas condiciones. Un proceso espontáneo ocurre sin la necesidad de un aporte continuo de energía de alguna fuente externa, mientras que un proceso no espontáneo lo requiere. Los sistemas sometidos a un proceso espontáneo pueden experimentar o no una ganancia o pérdida de energía, pero experimentarán un cambio en la forma en que la materia y/o la energía se distribuyen dentro del sistema.

    Glosario

    proceso no espontáneo
    proceso que requiere entrada continua de energía de una fuente externa
    cambio espontáneo
    proceso que se lleva a cabo sin una entrada continua de energía de una fuente externa

    Colaboradores

    This page titled 12.1: Espontaneidad is shared under a CC BY license and was authored, remixed, and/or curated by OpenStax.