Capítulo 10: Apéndice- Espectroscopia
- Page ID
- 76428
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
¿Cómo sabemos lo que sabemos de la estructura de la materia? Si piensas en nuestras discusiones sobre la estructura atómica, una de las pruebas más importantes de la naturaleza de los átomos —particularmente la disposición de sus electrones— fue la forma en que los átomos interactúan con la radiación electromagnética, es decir, la luz. Por ejemplo: la idea de que tanto la energía de la radiación electromagnética como la de los electrones se cuantifica vino del análisis de Einstein del efecto fotoeléctrico. Los electrones son expulsados de los metales solo si interactúan con fotones de cantidades suficientes y discretas de energía. Se aportó más evidencia de estados cuantificados de energía electrónica a partir del estudio de los espectros de absorción atómica y emisión, ya que los fotones de energía correspondientes a los huecos de energía entre los niveles de energía de los electrones son absorbidos o emitidos por electrones. Los fotones con la cantidad “incorrecta” de energía no son absorbidos. Ahora que hemos estudiado diferentes conjuntos de átomos (moléculas, iones, estructuras en red), también podemos observar cómo estas entidades más grandes interactúan con la energía (en forma de radiación electromagnética).
Interacciones de radiación electromagnética y electrones en moléculas: Como hemos visto, así como los electrones ocupan orbitales atómicos en átomos, los electrones en las moléculas ocupan orbitales moleculares. Al igual que con los orbitales atómicos, los electrones en los orbitales moleculares pueden absorber o liberar fotones de una energía específica a medida que se mueven de un orbital molecular a otro. Sin embargo, existe una diferencia significativa entre el proceso de absorción/emisión en átomos aislados (o iones) y el de las moléculas. Cuando un electrón es promovido a un nivel de energía más alto en un átomo, el producto es un átomo en un estado excitado —generalmente el átomo excitado (o ion) decaerá de nuevo al estado fundamental emitiendo un fotón. \(\mathrm{A} + hν \rightarrow \mathrm{A}^{*} (\text{excited state}) \rightarrow \mathrm{A} (\text{ground state}) + hν\)

Sin embargo, cuando un electrón dentro de una molécula es excitado se mueve (o es “promovido”) de su orbital molecular original a otro. Ahora hay una serie de consecuencias diferentes que pueden ocurrir. Por ejemplo, si el electrón absorbe un fotón y es promovido de un orbital molecular de unión a un orbital antienlace, el resultado será que el enlace se romperá, ya que ahora no hay interacción estabilizadora general. Considera\(\mathrm{H–H}\), que es la molécula más simple posible. El conjunto de orbitales moleculares para hidrógeno incluye un enlace σ y un orbital\(\sigma^{*}\) antienlace. En el estado de tierra (o energía más baja), el hidrógeno molecular tiene un orbital de enlace σ que contiene ambos electrones de la molécula. Si uno de los electrones de unión absorbe un fotón que tiene la cantidad justa de energía (la diferencia de energía entre el orbital de enlace y antienlace) se promoverá y se moverá hacia el orbital antienlace desestabilizado, haciendo que el enlace entre los átomos se rompa. Como se podría imaginar, si los enlaces químicos fueran susceptibles de romperse simplemente por estar expuestos a radiación electromagnética de baja energía, como la de la luz visible, el mundo sería un lugar diferente (y bastante aburrido). Por ejemplo, la vida no sería posible, ya que depende de la estabilidad de las moléculas.
La energía de los fotones requerida para provocar la ruptura del enlace es bastante grande. Por ejemplo, la energía requerida para romper un\(\mathrm{H–H}\) enlace (la energía de enlace) es\(436 \mathrm{~kJ/mol}\). Si se calcula la longitud de onda de un fotón que podría entregar esta cantidad de energía, la cantidad de energía requerida para romper un\(\mathrm{H–H}\) enlace estaría en la sección UV lejana del espectro electrogmagnético (\(\sim 280\mathrm{nm}\)). El enlace sigma (o sencillo) covalente típicamente fuerte requiere fotones de energía bastante alta para romperlos.

Entonces la pregunta es, si la atmósfera de la Tierra bloquea la mayoría (\(>98 \%\)) de los fotones de alta energía (ultravioleta) y las moléculas biológicamente más importantes no pueden absorber la luz visible, ¿por qué hay necesidad de protector solar, que filtra los fotones UV A (\(400-315 \mathrm{~nm}\)) y UV B (\(315-280 \mathrm{~nm}\)). La respuesta es que la mayoría de las moléculas biológicas contienen más que simples enlaces σ. Por ejemplo, la mayoría de las moléculas biológicas complejas también contienen enlaces π y electrones no enlazantes además de\(\sigma\) enlaces; se pueden observar transiciones entre estos orbitales ya que estos orbitales requieren menos energía para ser efectuados. Como se puede ver en la figura, las brechas de energía entre estos orbitales son bastante diferentes y son menores que la\(\sigma - \sigma^{*}\) diferencia. Los fotones con suficiente energía para provocar estas transiciones de electrones están presentes en la luz solar. Por ejemplo, un doble enlace tiene tanto a como\(\sigma\) a un\(\pi\) enlace. La absorción de un fotón que promovería un electrón de un orbital de enlace pi a un orbital\(\pi^{*}\) antienlace tendría el efecto de romper el\(\pi\) enlace original. Aquí se muestra una forma de representar esto\(\rightarrow\). Uno de los electrones que estaba en el\(\pi\) enlace se encuentra ahora en el orbital\(\pi^{*}\) antienlace de alta energía y es mucho más reactivo.
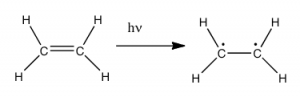
Otra forma de pensarlo es que los electrones ahora están desapareados, y es mucho más probable que reaccionen para formar una entidad más estable. [1] Una manera obvia de recuperar la estabilidad es que el electrón en el orbital\(\pi\) antienlace vuelva a caer al nivel de energía de unión y emita un fotón de la misma energía, y en la mayoría de los casos esto es lo que sucede, en última instancia, sin causar daño. Una advertencia aquí es que dado que los dobles enlaces están rotacionalmente restringidos, es posible que la rotación pueda ocurrir alrededor del enlace simple (\(\sigma\)) antes de las reformas del enlace π; esto conduce a un isómero del alqueno original. Por otro lado, si hay una especie potencialmente reactiva cercana, pueden ocurrir reacciones entre moléculas (o en el caso de macromoléculas biológicas, entre distintas regiones de estas moléculas). Por ejemplo, la mayoría de nosotros somos conscientes de que la exposición al sol causa daños en la piel que pueden llevar al cáncer de piel. Un mecanismo importante para estos efectos implica\(\mathrm{DNA}\). Donde dos bases de timidina están adyacentes entre sí, un fotón UV puede ser absorbido por un enlace π en una base de timina. Este enlace π roto (y el electrón desapareado resultante) es muy reactivo. Puede reaccionar con un enlace π en una timina-moeity adyacente conduciendo a un nuevo enlace, una reacción que produce un anillo de carbono de cuatro miembros, conocido como dímero de timina. La maquinaria de\(\mathrm{DNA}\) replicación no puede replicar con precisión una secuencia que contiene un dímero de timina, lo que resulta en un cambio en la\(\mathrm{DNA}\) secuencia, una mutación. Las mutaciones de este tipo son un paso temprano común en la generación de células cancerosas de la piel. [2]

Un ejemplo más benigno de absorción de fotones en sistemas biológicos subyace al mecanismo por el cual nosotros (y otros organismos) detectamos la luz, ¡así podemos ver las cosas! Si bien originalmente se pensaba (al menos por algunos) que la visión involucraba rayos emitidos por los ojos, [3] ahora entendemos que para ver necesitamos detectar fotones que son reflejados o emitidos por los objetos que nos rodean. El proceso comienza cuando los fotones de luz caen sobre las células conocidas como fotorreceptores. A nuestros ojos, estas células se encuentran dentro de la retina, una lámina de células que recubren la superficie interior del ojo. Dentro de un subconjunto de células retinianas hay varios tipos diferentes de moléculas que contienen enlaces π. Estas moléculas son proteínas conocidas genéricamente como opsinas. Una opsina está compuesta por un polipéptido (o apoproteína) que se une covalentemente a otra molécula, 11-cis-retinal. [4] Esta molécula se deriva de la vitamina A (todo trans retinol). El complejo de apoproteína y retinal es la proteína opsina funcional. Hay una serie de diferentes componentes de opsina que influyen en la longitud de onda de los fotones absorbidos por la proteína opsina funcional. Cuando se absorbe un fotón, promueve un electrón de uno de los enlaces π de la retina (entre\(C_{11}\) y\(C_{12}\)) a un orbital antienlace. En lugar de reaccionar con otra molécula, como la timina, hay una rotación alrededor del enlace single (\(\sigma\)) restante, y luego la re-formación del\(\pi\) enlace, lo que conduce a la isomerización de la forma 11-cis original en el isómero trans. Este cambio en la forma del resto retiniano a su vez influye en la forma de la proteína opsina que inicia una cascada de eventos electroquímicos que transportan señales al resto del cerebro (la retina se considera una extensión del cerebro) que finalmente son reconocidas como entrada visual.

Espectroscopia UV-Vis y cromóforos — o ¿por qué las zanahorias son naranjas? Una recomendación común de los médicos es que comamos muchas frutas y verduras altamente coloreadas. Los compuestos que dan a estos alimentos su color fuerte tienen una serie de puntos en común. Por ejemplo, el compuesto que le da a las zanahorias y batatas su distintivo color naranja es el betacaroteno. Bien podría notar su similitud con la retina. El compuesto que contribuye al color rojo de los tomates es el licopeno. Las moléculas de este tipo se conocen genéricamente como pigmentos.
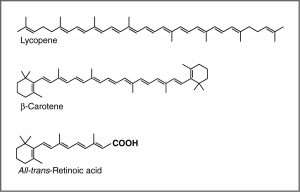
Las longitudes de onda a las que un compuesto absorbe la luz depende de la brecha de energía entre los orbitales que están involucrados en la transición. Esta brecha de energía está determinada por la estructura de la molécula. Una molécula con solo enlaces simples absorbe la luz a longitudes de onda más cortas (en los UV de alta energía), mientras que patrones de unión más complejos se asocian con la absorción de luz visible. Por ejemplo, la presencia de múltiples enlaces π y sus interacciones dentro de la molécula pueden afectar la brecha de energía entre los orbitales moleculares. Recordemos nuestra discusión sobre el grafito. En lugar de pensar en el grafito como láminas de anillos fusionados de seis miembros con enlaces simples y dobles alternantes, podemos pensar en cada enlace como un enlace σ localizado y un enlace π deslocalizado. Hay un gran número de orbitales\(\pi\) moleculares repartidos por toda la lámina de átomos de carbono. Cuantos más\(\pi\) MO haya, más disminuye la brecha de energía entre estas disminuciones orbitales, es decir, menos energía (luz de longitud de onda más larga) se necesita para mover un electrón de\(\pi\) a\(\pi^{*}\) orbital. En el caso de las sustancias de red como el grafito y los metales, la brecha energética entre los orbitales se vuelve insignificante, y pensamos en el modelo de unión como una banda de orbitales moleculares. En estos casos, muchas longitudes de onda de luz pueden ser absorbidas y luego reemitidas lo que le da al grafito y a los metales su brillo característico. En sustancias como el licopeno o\(\beta\) -caroteno también encontramos este patrón de alternancia de enlaces simples y dobles. Decimos que los compuestos con este patrón de enlaces simples y dobles alternantes (e.g.\(\mathrm{–C=C–C=C–}\)) se conjugan, y podemos modelar la unión de la misma manera que el grafito. Hay\(\pi\) MO que pueden extenderse sobre la región de la molécula, y cuantos más orbitales haya, más cerca se acercan en energía.
Para un\(\mathrm{C=C}\) doble enlace aislado, la energía requerida para promover un electrón del\(\pi\) al\(\pi^{*}\) orbital corresponde a la luz en la región UV (alrededor\(170 \mathrm{~nm}\)), pero a medida que aumenta el número de dobles enlaces que se conjugan (separados por enlaces simples), la brecha de energía entre disminuye el orbital molecular ocupado más alto (HOMO) y el orbital molecular desocupado más bajo (LUMO). Finalmente, la longitud de onda de la luz necesaria para promover un electrón del HOMO al LUMO se mueve hacia la región visible, y la sustancia se vuelve coloreada. (Obsérvese que no se convierte en el color de la luz que se absorbe, sino en la luz restante que se transmite o refleja). Estas regiones conjugadas de moléculas se denominan cromóforos. [5] Cuanto más larga sea la sección conjugada de la molécula, mayor será la longitud de onda que se absorbe. Notarás que tanto el licopeno como el B-caroteno contienen grandes regiones cromóforos.

Aquí se muestran muestras de espectros de absorción UV-VIS. Nótese que en contraste con los espectros de absorción atómica que vimos anteriormente que consistían en líneas nítidas correspondientes a la longitud de onda de la luz absorbida por los átomos, estos espectros son amplios y mal definidos. Además, se puede ver que cuanto más largo (más grande) es el cromóforo, más larga es la longitud de onda que se absorbe, y cada uno de estos compuestos parece ser de un color diferente.
El hecho de que los picos en estos espectros no sean agudos significa que la espectroscopia UV-VIS normalmente no se usa para la identificación de compuestos (ver a continuación para la espectroscopia IR y RMN que se puede usar para este propósito). Sin embargo, la cantidad de luz absorbida es proporcional a la concentración de la sustancia y, por lo tanto, se puede utilizar la espectroscopia UV-VIS para determinar la concentración de las muestras. Existen otros comportamientos ópticos asociados a moléculas complejas en los organismos, entre ellos los sistemas moleculares que emiten luz, proceso conocido como bioluminiscencia que no discutiremos aquí. [6]
Espectroscopia infrarroja — mirando las vibraciones moleculares: Hasta ahora nos hemos concentrado en la absorción (y emisión) de energía causada por las transiciones de electrones entre niveles de energía cuantificados. Sin embargo, como discutimos anteriormente, las energías electrónicas no son las únicas energías cuantificadas a nivel atómico-molecular. En las moléculas, también se cuantifican las energías tanto de las vibraciones moleculares como de las rotaciones, pero las energías involucradas son mucho más bajas que las necesarias para romper los enlaces. Cuando dos átomos están unidos, los átomos pueden moverse de un lado a otro: a medida que se mueven, la energía potencial del sistema de dos átomos cambia (¿por qué es eso?). También hay movimientos asociados con rotaciones alrededor de los bonos. Pero (extrañamente, y mecánicamente cuántico) en lugar de poder asumir cualquier valor, también se cuantifican las energías de estas vibraciones (y rotaciones). Las brechas de energía entre los niveles de energía vibratoria tienden a estar en el rango de radiación infrarroja. Cuando miramos la luz absorbida o emitida por los cambios de energía vibratoria estamos haciendo lo que se conoce como espectroscopia infrarroja. Las transiciones de un nivel de energía rotacional a antera pueden ser promovidas por la radiación de microondas, lo que lleva a la espectroscopia de microondas La siguiente tabla proporciona ejemplos de diferentes tipos de espectroscopía, la longitud de onda de la radiación electromagnética típicamente involucrada y los usos de cada tipo de espectroscopia.
| Tipo de Espectroscopia | Longitud de onda de radiación | Interacción con la materia | Propósito |
|---|---|---|---|
| UV-VIS | \(350-700 \mathrm{~nm}\) | Transiciones electrónicas en moléculas | A menudo se utiliza para determinar concentraciones |
| IR | \(2,500-16,000 \mathrm{~nm}\) | Vibraciones moleculares | Determinar la presencia de grupos particulares de átomos (grupos funcionales |
| RMN | \(10-100 \mathrm{~m}\) | Transiciones nucleares | Identificar tipos de C y H en moléculas |
| RESONANCIA MAGNÉTICA | \(10-100 \mathrm{~m}\) | Transiciones nucleares | Imágenes (normalmente partes del cuerpo humano) |

¿Por qué, podría preguntarse, nos interesan las vibraciones y rotaciones de las moléculas? Resulta que muchas moléculas y fragmentos de moléculas tienen patrones de absorción IR muy distintivos que pueden usarse para identificarlos. La figura muestra un espectro IR de un ácido carboxílico y cómo los diversos picos pueden atribuirse a vibraciones de diferentes enlaces o grupos dentro de la molécula. La espectroscopia infrarroja nos permite identificar sustancias a partir de estos patrones, tanto en el laboratorio como por ejemplo en nubes de polvo interestelares. La presencia de moléculas bastante complejas en el espacio (a cientos de millones de años luz de distancia de la tierra) se ha detectado mediante el uso de la espectroscopia IR.

Espectroscopia de Resonancia Magnética Nuclear (RMN): La RMN es una forma de espectroscopia que utiliza el hecho de que ciertos núcleos pueden, dependiendo de su estructura, comportarse como pequeños imanes giratorios. Dos de los núcleos más comunes utilizados para la espectroscopia de RMN son\({}^{1}\mathrm{H}\) y\({}^{13}\mathrm{C}\). Cuando los materiales que contienen átomos de carbono o hidrógeno en ellos se colocan en un campo magnético, existen dos posibles orientaciones de estos núcleos con respecto al campo: una orientación de baja energía en la que el imán nuclear se alinea con el campo, y una orientación de alta energía en la que imán nuclear está alineado contra el campo. El efecto de esto es dividir los niveles de energía de los núcleos. Esto permite provocar una transición entre los dos niveles de energía por la absorción de radiación electromagnética de la energía apropiada- que en este caso, se encuentra en el rango de ondas de radio.
La energía exacta de estos cambios depende del ambiente de los núcleos, si el\(\mathrm{C}\) o\(\mathrm{H}\) está en un ambiente deficiente en electrones aparecerá a una frecuencia diferente en el espectro que a\(\mathrm{C}\) o\(\mathrm{H}\) que está rodeado por más densidad de electrones (se dice que el núcleo es blindado por los electrones.) A partir de un estudio de las diferentes energías absorbidas a medida que el núcleo voltea de un estado de espín a otro, es posible derivar información sobre la estructura del compuesto.
La información que se puede obtener a partir de espectros de RMN simples tiene que ver con el número y tipo de núcleos que se encuentran en un determinado compuesto. El tipo más simple de espectro de RMN se basa en\({}^{13}\mathrm{C}\). \({}^{13}\mathrm{C}\)es un isótopo menor de carbono (aproximadamente 1% de la abundancia natural) y está presente en todas las muestras naturales de compuestos de carbono. En un\({}^{13}\mathrm{C}\) espectro, cada átomo de carbono en la molécula dará lugar a una señal o pico en el espectro basado en su entorno químico. Por ejemplo, el etanol (\(\mathrm{CH}_{3}\mathrm{CH}_{2}\mathrm{OH}\)) tiene dos picos en su\({}^{13}\mathrm{C}\) espectro porque hay dos, y solo dos ambientes químicos distintos en los que un átomo de carbono puede “habitar”. En contraste, la ciclohexenona produce un espectro que tiene seis picos distintos, ya que cada uno de los seis átomos de carbono de la molécula habita en un ambiente claramente diferente. El benceno (\(\mathrm{C}_{6}\mathrm{H}_{6}\)) por otro lado solo tiene una señal en su espectro de\({}^{13}\mathrm{C}\) RMN ya que solo hay un tipo de carbono en esta molécula, todas las posiciones en el anillo son equivalentes. (Dibuja la estructura de Lewis para convencerte de que esto es cierto)



Los espectros de protones o\({}^{1}\mathrm{H}\) RMN parecen más complicados porque cada átomo de hidrógeno tiende a dar una señal que se divide en varios picos diferentes. Esto se debe a que cada\(\mathrm{H}\) núcleo puede ser afectado por los núcleos vecinos. Esto produce múltiples niveles de energía para cada uno\(\mathrm{H}\), lo que resulta en espectros más complejos. \({}^{13}\mathrm{C}\)parece más simple porque normalmente solo hay un\({}^{13}\mathrm{C}\) núcleo (o cero) en cualquier molécula, por lo tanto no hay interacciones por carbonos cercanos (\({}^{12}\mathrm{C}\)no tiene diferentes niveles de energía nuclear en un campo magnético). Obsérvese que este espectro de\({}^{1}\mathrm{H}\) RMN es mucho más complejo que el\({}^{13}\mathrm{C}\) RMN. Sin embargo, hay cinco grupos distintos de señales y hay cinco tipos de protones en el compuesto que da origen a este espectro
Una variante de la RMN es la Resonancia Magnética (MRI), que se basa en los mismos comportamientos nucleares subyacentes, pero utiliza un enfoque algo diferente. En MRI el material (generalmente una persona) del que se desea registrar el espectro se coloca en un imán grande que separa los estados de espín nuclear como se describió anteriormente. El objetivo es irradiado con un pulso de ondas de radio que promueve todos los núcleos hasta su estado energético más alto accesible. A medida que los núcleos se descomponen de nuevo al estado de espín inferior, emiten fotones. En lugar de detectar las energías de estos fotones, el sistema registra los tiempos que tardan en emitirse los fotones a medida que los núcleos vuelven a caer a sus estados de energía más bajos. Estos tiempos dependen del entorno de los núcleos haciendo posible, a través de la manipulación de datos, desarrollar visualizaciones internas del cuerpo en el escáner.
Estos son solo algunos tipos de ejemplos de espectroscopia. Hay muchos más que puedes encontrar, pero normalmente estos métodos dependen todos de registrar cómo interactúan la materia y la energía y usar esos datos para determinar la disposición de los átomos en la materia que se está investigando.
Miniatura: La luz blanca se dispersa por un prisma en los colores del espectro visible. (CC BY-SA 3.0; D-Kuru).


