16.2: Entropía

Objetivos de aprendizaje

• Definir entropía
• Explicar la relación entre la entropía y el número de microestados
• Predecir el signo del cambio de entropía para procesos químicos y físicos

En 1824, a la edad de 28 años, Nicolas Léonard Sadi Carnot (Figura\(\PageIndex{2}\)) publicó los resultados de un extenso estudio sobre la eficiencia de las máquinas de calor de vapor. En una revisión posterior de los hallazgos de Carnot, Rudolf Clausius introdujo una nueva propiedad termodinámica que relaciona el flujo de calor espontáneo que acompaña a un proceso con la temperatura a la que se lleva a cabo el proceso. Esta nueva propiedad se expresó como la relación entre el calor reversible (q _rev) y la temperatura Kelvin (T). El término proceso reversible se refiere a un proceso que tiene lugar a un ritmo tan lento que siempre está en equilibrio y su dirección puede ser cambiada (puede ser “invertida”) por un cambio infinitesimalmente pequeño es alguna condición. Nótese que la idea de un proceso reversible es un formalismo requerido para apoyar el desarrollo de diversos conceptos termodinámicos; ningún proceso real es verdaderamente reversible, sino que se clasifica como irreversibles.

Figura\(\PageIndex{1}\): (a) La investigación de Nicholas Léonard Sadi Carnot sobre maquinaria a vapor y (b) el estudio posterior de Rudolf Clausius de esos hallazgos condujeron a descubrimientos innovadores sobre procesos espontáneos de flujo de calor.

Similar a otras propiedades termodinámicas, esta nueva cantidad es una función de estado, por lo que su cambio depende únicamente de los estados inicial y final de un sistema. En 1865, Clausius nombró esta propiedad entropía (S) y definió su cambio para cualquier proceso de la siguiente manera:

\[ΔS=\dfrac{q_\ce{rev}}{T} \label{Eq1} \]

El cambio de entropía para un proceso real e irreversible es entonces igual al del proceso teórico reversible que involucra los mismos estados inicial y final.

Entropía y Microestados

Siguiendo el trabajo de Carnot y Clausius, Ludwig Boltzmann desarrolló un modelo estadístico a escala molecular que relacionó la entropía de un sistema con el número de microestados posibles para el sistema. Un microestado (\(\Omega\))es una configuración específica de las ubicaciones y energías de los átomos o moléculas que comprenden un sistema como el siguiente:

\[S=k \ln \Omega \label{Eq2} \]

Aquí k es la constante de Boltzmann y tiene un valor de\(1.38 \times 10^{−23}\, J/K\).

En cuanto a otras funciones de estado, el cambio en la entropía para un proceso es la diferencia entre sus valores final (S _f) e inicial (S _i):

\[\begin{align} ΔS &=S_\ce{f}−S_\ce{i} \nonumber \\[4pt] &=k \ln \Omega_\ce{f} − k \ln \Omega_\ce{i} \nonumber \\[4pt] &=k \ln\dfrac{\Omega_\ce{f}}{\Omega_\ce{i}} \label{Eq2a} \end{align} \]

Para procesos que implican un incremento en el número de microestados del sistema\(\Omega_f > \Omega_i\),, la entropía del sistema aumenta,\(ΔS > 0\). Por el contrario, los procesos que reducen el número de microestados en el sistema,\(\Omega_f < \Omega_i\), producen una disminución en la entropía del sistema,\(ΔS < 0\). Esta interpretación de la entropía a escala molecular proporciona un vínculo con la probabilidad de que ocurra un proceso como se ilustra en los párrafos siguientes.

Figura\(\PageIndex{2}\): Se muestran los dieciséis microestados asociados con la colocación de cuatro partículas en dos cajas. Los microestados se recolectan en cinco distribuciones —( a), (b), (c), (d) y (e) —basadas en el número de partículas en cada caja.

Se muestran cinco filas de diagramas que parecen dominó y se etiquetan como a, b, c, d y e. La fila a tiene un “dominó” que tiene cuatro puntos en el lado izquierdo, rojo, verde, azul y amarillo en un patrón en el sentido de las agujas del reloj desde la parte superior izquierda, y ningún punto a la derecha. La fila b tiene cuatro “dominó”, cada uno con tres puntos a la izquierda y un punto a la derecha. El primero muestra un “dominó” con verde, amarillo y azul a la izquierda y rojo a la derecha. El segundo “dominó” tiene amarillo, azul y rojo a la izquierda y verde a la derecha. El tercer “dominó” tiene rojo, verde y amarillo a la izquierda y azul a la derecha mientras que el cuarto tiene rojo, verde y azul a la izquierda y amarillo a la derecha. La fila c tiene seis “dominó”, cada uno con dos puntos a cada lado. El primero tiene un rojo y verde a la izquierda y un azul y amarillo a la derecha. El segundo tiene un rojo y azul a la izquierda y un verde y amarillo a la derecha mientras que el tercero tiene un amarillo y rojo a la izquierda y un verde y azul a la derecha. El cuarto tiene un verde y azul a la izquierda y un rojo y amarillo a la derecha. El quinto tiene un verde y amarillo a la izquierda y un rojo y azul a la derecha. El sexto tiene un azul y amarillo a la izquierda y un verde y rojo a la derecha. La fila d tiene cuatro “dominó”, cada uno con un punto a la izquierda y tres a la derecha. El primer “dominó” tiene rojo a la izquierda y un azul, verde y amarillo a la derecha. El segundo tiene un verde a la izquierda y un rojo, amarillo y azul a la derecha. El tercero tiene un azul a la izquierda y un rojo, verde y amarillo a la derecha. El cuarto tiene un amarillo a la izquierda y un rojo, verde y azul a la derecha. La fila e tiene 1 “dominó” sin puntos a la izquierda y cuatro puntos a la derecha que son rojos, verdes, azules y amarillos.

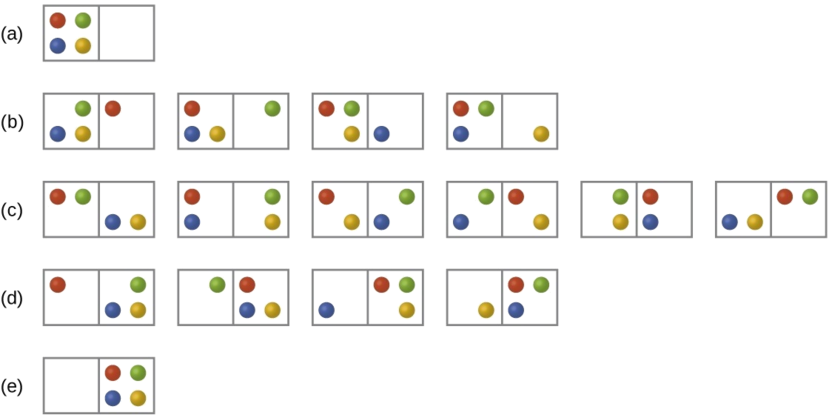
Consideremos el caso general de un sistema compuesto por partículas de N distribuidas entre n cajas. El número de microestados posibles para dicho sistema es n ^N. Por ejemplo, la distribución de cuatro partículas entre dos cajas dará como resultado 2 ⁴ = 16 microestados diferentes como se ilustra en la Figura\(\PageIndex{2}\). Los microestados con arreglos de partículas equivalentes (sin considerar identidades de partículas individuales) se agrupan y se denominan distribuciones (a veces llamadas macroestados o configuraciones). La probabilidad de que exista un sistema con sus componentes en una distribución dada es proporcional al número de microestados dentro de la distribución. Dado que la entropía aumenta logarítmicamente con el número de microestados, la distribución más probable es, por lo tanto, la de mayor entropía.

Para este sistema, la configuración más probable es uno de los seis microestados asociados a la distribución (c) donde las partículas se distribuyen uniformemente entre las cajas, es decir, una configuración de dos partículas en cada caja. La probabilidad de encontrar el sistema en esta configuración es

 

\[\dfrac{6}{16} = \dfrac{3}{8} \nonumber \]

La configuración menos probable del sistema es aquella en la que las cuatro partículas están en una caja, correspondientes a las distribuciones (a) y (e), cada una con una probabilidad de

\[\dfrac{1}{16} \nonumber \]

La probabilidad de encontrar todas las partículas en un solo cuadro (ya sea el cuadro izquierdo o el cuadro derecho) es entonces

\[\left(\dfrac{1}{16}+\dfrac{1}{16}\right)=\dfrac{2}{16} = \dfrac{1}{8} \nonumber \]

 

A medida que agrega más partículas al sistema, el número de microestados posibles aumenta exponencialmente (2 ^N). Un sistema macroscópico (del tamaño de laboratorio) normalmente consistiría en moles de partículas (N ~ 10 ²³), y el número correspondiente de microestados sería asombrosamente enorme. Sin embargo, independientemente del número de partículas en el sistema, las distribuciones en las que se encuentran números aproximadamente iguales de partículas en cada caja son siempre las configuraciones más probables.

La distribución más probable es, por tanto, la de mayor entropía.

La descripción anterior de un gas ideal que se expande en vacío es un ejemplo macroscópico de este modelo de partículas en caja. Para este sistema, se confirma que la distribución más probable es aquella en la que la materia se dispersa o distribuye de manera más uniforme entre los dos matraces. El proceso espontáneo mediante el cual el gas contenido inicialmente en un matraz se expande para llenar ambos matraces por igual, por lo tanto, produce un aumento en la entropía para el sistema.

Figura\(\PageIndex{3}\): Muestra un modelo de microestados que describe el flujo de calor de un objeto caliente a un objeto frío. (a) Antes de que ocurra el flujo de calor, el objeto compuesto por partículas A y B contiene ambas unidades de energía y como se representa por una distribución de tres microestados. (b) Si el flujo de calor resulta en una dispersión uniforme de la energía (una unidad de energía transferida), resulta una distribución de cuatro microestados. c) Si se transfieren ambas unidades de energía, la distribución resultante tiene tres microestados.

Se muestran tres filas etiquetadas a, b y c y cada una contiene rectángulos con dos lados donde el lado izquierdo está etiquetado, “A” y “B”, y el derecho está etiquetado, “C” y “D” La fila a tiene tres rectángulos donde el primero tiene un punto por encima y por debajo de la letra A, el segundo tiene un punto por encima de A y B, y el tercero que tiene un punto por encima y por debajo de la letra B. La fila b tiene cuatro rectángulos; la primera tiene un punto por encima de A y C, la segunda tiene un punto por encima de A y D, la tercera tiene un punto por encima de B y C y el cuarto tiene un punto por encima de B y D. La fila c tiene tres rectángulos; el primero tiene un punto por encima y por debajo de la letra C, el segundo tiene un punto por encima de C y D y el tercero tiene un punto por encima y por debajo de la letra D.

Se puede usar un enfoque similar para describir el flujo espontáneo de calor. Considera un sistema que consta de dos objetos, cada uno conteniendo dos partículas, y dos unidades de energía (representadas como “*”) en la Figura\(\PageIndex{3}\). El objeto caliente está compuesto por partículas A y B e inicialmente contiene ambas unidades de energía. El objeto frío está compuesto por partículas C y D, que inicialmente no tiene unidades de energía. La distribución (a) muestra los tres microestados posibles para el estado inicial del sistema, con ambas unidades de energía contenidas dentro del objeto caliente. Si se transfiere una de las dos unidades de energía, el resultado es la distribución (b) que consta de cuatro microestados. Si se transfieren ambas unidades de energía, el resultado es la distribución (c) que consta de tres microestados. Y así, podemos describir este sistema por un total de diez microestados. La probabilidad de que el calor no fluya cuando los dos objetos se ponen en contacto, es decir, que el sistema permanezca en distribución (a), es\(\frac{3}{10}\). Más probable es que el flujo de calor produzca una de las otras dos distribuciones, siendo la probabilidad combinada\(\frac{7}{10}\). El resultado más probable es el flujo de calor para producir la dispersión uniforme de energía representada por la distribución (b), siendo la probabilidad de esta configuración\(\frac{4}{10}\). En cuanto al ejemplo anterior de dispersión de materia, extrapolar este tratamiento a colecciones macroscópicas de partículas aumenta drásticamente la probabilidad de la distribución uniforme en relación con las otras distribuciones. Esto respalda la observación común de que la colocación de objetos fríos y calientes en contacto da como resultado un flujo de calor espontáneo que finalmente iguala las temperaturas de los objetos. Y, nuevamente, este proceso espontáneo también se caracteriza por un incremento en la entropía del sistema.

Ejemplo\(\PageIndex{1}\): Determination of ΔS

Considera el sistema que se muestra aquí. ¿Cuál es el cambio en la entropía para un proceso que convierte el sistema de distribución (a) a (c)?

 

Un diagrama muestra un rectángulo con dos lados que tiene cuatro puntos, rojo, verde, amarillo y azul escritos en el lado izquierdo. Una flecha orientada hacia la derecha conduce a seis rectángulos de dos lados más, cada uno con dos puntos en los lados izquierdo y derecho. El primer rectángulo tiene un punto rojo y verde a la izquierda y un azul y amarillo a la derecha, mientras que el segundo muestra un rojo y azul a la izquierda y un verde y amarillo a la derecha. El tercer rectángulo tiene un punto rojo y amarillo a la izquierda y un azul y verde a la derecha, mientras que el cuarto muestra un verde y azul a la izquierda y un rojo y amarillo a la derecha. El quinto rectángulo tiene un punto amarillo y verde a la izquierda y un azul y rojo a la derecha, mientras que el sexto muestra un amarillo y azul a la izquierda y un verde y rojo a la derecha.

Solución

Nos interesa el siguiente cambio:

El número inicial de microestados es uno, los seis finales:

\[\begin{align} ΔS &=k \ln\dfrac{\Omega_\ce{c}}{\Omega_\ce{a}} \nonumber \\[4pt] &= 1.38×10^{−23}\:J/K × \ln\dfrac{6}{1} \nonumber \\[4pt] &= 2.47×10^{−23}\:J/K \nonumber \end{align} \nonumber \]

El signo de este resultado es consistente con la expectativa; dado que hay más microestados posibles para el estado final que para el estado inicial, el cambio en la entropía debería ser positivo.

Ejercicio\(\PageIndex{1}\)

Considere el sistema que se muestra en la Figura\(\PageIndex{3}\). ¿Cuál es el cambio en la entropía para el proceso donde toda la energía se transfiere del objeto caliente (AB) al objeto frío (CD)?

Contestar

0 J/K

Predecir el Signo de Δ S

Las relaciones entre entropía, microestados y dispersión materia/energía descritas anteriormente permiten hacer generalizaciones con respecto a las entropías relativas de sustancias y predecir el signo de cambios de entropía para procesos químicos y físicos. Considere los cambios de fase ilustrados en la Figura\(\PageIndex{4}\). En la fase sólida, los átomos o moléculas están restringidos a posiciones casi fijas entre sí y solo son capaces de oscilaciones modestas alrededor de estas posiciones. Con ubicaciones esencialmente fijas para las partículas componentes del sistema, el número de microestados es relativamente pequeño. En la fase líquida, los átomos o moléculas son libres de moverse unos sobre otros, aunque permanecen relativamente cerca unos de otros. Esta mayor libertad de movimiento da como resultado una mayor variación en las posibles ubicaciones de las partículas, por lo que el número de microestados es correspondientemente mayor que para el sólido. Como resultado, S _líquido > S _sólido y el proceso de conversión de una sustancia de sólido a líquido (fusión) se caracteriza por un aumento en la entropía, Δ S > 0. Por la misma lógica, el proceso recíproco (congelación) exhibe una disminución en la entropía, Δ S < 0.

Figura\(\PageIndex{4}\): La entropía de una sustancia aumenta (ΔS > 0) a medida que se transforma de un sólido relativamente ordenado, a un líquido menos ordenado, y luego a un gas aún menos ordenado. La entropía disminuye (ΔS < 0) a medida que la sustancia se transforma de un gas a un líquido y luego a un sólido.

Tres matraces tapados se muestran con flechas orientadas hacia la derecha e izquierda entre cada uno; el primero se etiqueta arriba como, “delta S mayor que 0”, y debajo como, “delta S menor que 0”, mientras que el segundo se etiqueta arriba como, “delta S mayor que 0”, y debajo como, “delta S menor que 0”. Se dibuja una flecha larga orientada hacia la derecha sobre todos los matraces y se etiqueta como “Entropía creciente”. El matraz izquierdo contiene veintisiete partículas dispuestas en un cubo en el fondo del matraz y está etiquetado como “Sólido cristalino” a continuación. El matraz del medio contiene veintisiete partículas dispersas aleatoriamente en el fondo del matraz y está etiquetado como “Líquido” a continuación. El matraz derecho contiene veintisiete partículas dispersas dentro del matraz y que se mueven rápidamente y se etiqueta como “Gas”, abajo.

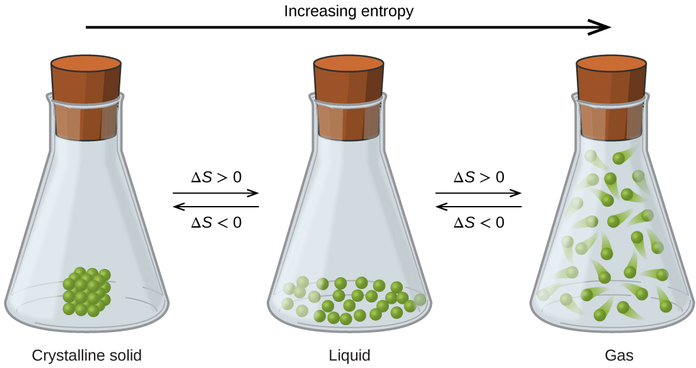
Ahora considere la fase vapor o gas. Los átomos o moléculas ocupan un volumen mucho mayor que en la fase líquida; por lo tanto, cada átomo o molécula se puede encontrar en muchas más ubicaciones que en la fase líquida (o sólida). En consecuencia, para cualquier sustancia, _gas S > S _líquido > S _sólido, y los procesos de vaporización y sublimación implican igualmente incrementos en la entropía, Δ S > 0. Asimismo, las transiciones de fase recíprocas, condensación y deposición, implican disminuciones en la entropía, Δ S < 0.

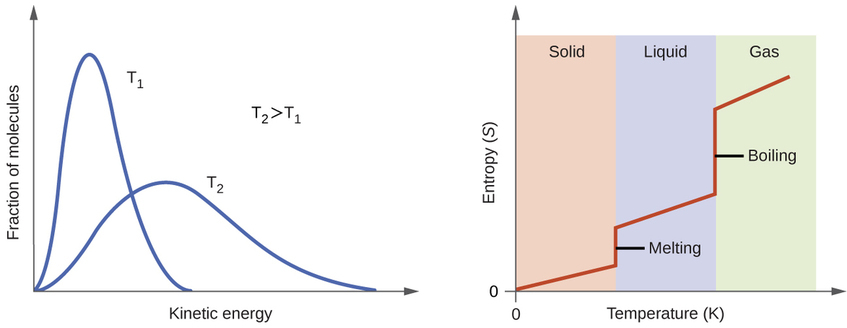
Según la teoría cinético-molecular, la temperatura de una sustancia es proporcional a la energía cinética promedio de sus partículas. El aumento de la temperatura de una sustancia dará como resultado vibraciones más extensas de las partículas en sólidos y traducciones más rápidas de las partículas en líquidos y gases. A temperaturas más altas, la distribución de las energías cinéticas entre los átomos o moléculas de la sustancia también es más amplia (más dispersa) que a temperaturas más bajas. Así, la entropía para cualquier sustancia aumenta con la temperatura (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): La entropía aumenta a medida que se eleva la temperatura de una sustancia, lo que corresponde a la mayor dispersión de las energías cinéticas. Cuando una sustancia se funde o vaporiza, experimenta un aumento significativo en la entropía.

Se muestran dos gráficas. El eje y de la gráfica izquierda está etiquetado como “Fracción de moléculas”, mientras que el eje x está etiquetado, “Velocidad, v (m/s)”, y tiene valores de 0 a 1,500 a lo largo del eje con incrementos de 500. En esta gráfica se trazan cuatro líneas. El primero, etiquetado, “100 K”, alcanza un pico alrededor de 200 m/ s, mientras que el segundo, etiquetado con “200 K”, alcanza un pico cerca de 300 m/ s y es ligeramente menor en el eje y que el primero. La tercera línea, etiquetada con “500 K”, alcanza un pico alrededor de 550 m/ s y es menor que las dos primeras en el eje y. La cuarta línea, etiquetada con “1000 K”, alcanza un pico alrededor de 750 m/ s y es la más baja de las cuatro en el eje y. Cada línea se vuelve cada vez más amplia. La segunda gráfica tiene un eje y etiquetado como “Entropía, S”, con una flecha orientada hacia arriba y un eje x etiquetado como “Temperatura (K)” y una flecha orientada hacia la derecha. La gráfica tiene tres columnas igualmente espaciadas en el fondo, etiquetadas como “Sólido”, “Líquido” y, “Gas”, de izquierda a derecha. Una línea se extiende ligeramente hacia arriba a través de la primera columna en una ligera dirección ascendente, luego va recto hacia arriba en la transición entre las dos primeras columnas. En entonces avanza en una ligera dirección ascendente a través de la segunda columna, luego sube dramáticamente entre la segunda y tercera columnas, luego continúa en una ligera dirección ascendente una vez más. La primera región vertical de esta línea está etiquetada como “Fusión” y la segunda está etiquetada como “Hervido”.

La entropía de una sustancia está influenciada por la estructura de las partículas (átomos o moléculas) que comprenden la sustancia. Con respecto a las sustancias atómicas, los átomos más pesados poseen mayor entropía a una temperatura dada que los átomos más ligeros, lo que es consecuencia de la relación entre la masa de una partícula y el espaciamiento de los niveles de energía traslacional cuantificados (que es un tema más allá del alcance de nuestro tratamiento). Para las moléculas, un mayor número de átomos (independientemente de sus masas) aumenta las formas en que las moléculas pueden vibrar y así el número de microestados posibles y la entropía del sistema.

Finalmente, las variaciones en los tipos de partículas afectan la entropía de un sistema. En comparación con una sustancia pura, en la que todas las partículas son idénticas, la entropía de una mezcla de dos o más tipos de partículas diferentes es mayor. Esto se debe a las orientaciones e interacciones adicionales que son posibles en un sistema compuesto por componentes no idénticos. Por ejemplo, cuando un sólido se disuelve en un líquido, las partículas del sólido experimentan tanto una mayor libertad de movimiento como interacciones adicionales con las partículas de disolvente. Esto corresponde a una dispersión más uniforme de materia y energía y a un mayor número de microestados. Por lo tanto, el proceso de disolución implica un aumento de la entropía, Δ S > 0.

Considerando los diversos factores que afectan a la entropía nos permite hacer predicciones informadas del signo de Δ S para diversos procesos químicos y físicos como se ilustra en Ejemplo.

Ejemplo\(\PageIndex{2}\): Predicting the Sign of ∆S

Predecir el signo del cambio de entropía para los siguientes procesos. Indica el motivo de cada una de tus predicciones.

1. Un mol de agua líquida a temperatura ambiente\(⟶\) un mol de agua líquida a 50 °C
2. \(\ce{Ag+}(aq)+\ce{Cl-}(aq)⟶\ce{AgCl}(s)\)
3. \(\ce{C6H6}(l)+\dfrac{15}{2}\ce{O2}(g)⟶\ce{6CO2}(g)+\ce{3H2O}(l)\)
4. \(\ce{NH3}(s)⟶\ce{NH3}(l)\)

S olución

1. positivo, aumenta la temperatura
2. negativo, reducción en el número de iones (partículas) en solución, disminución de la dispersión de materia
3. negativo, disminución neta en la cantidad de especies gaseosas
4. positivo, transición de fase de sólido a líquido, aumento neto en la dispersión de materia

Ejercicio\(\PageIndex{2}\)

Predecir el signo del cambio de entalpía para los siguientes procesos. Da una razón para tu predicción.

1. \(\ce{NaNO3}(s)⟶\ce{Na+}(aq)+\ce{NO3-}(aq)\)
2. la congelación de agua líquida
3. \(\ce{CO2}(s)⟶\ce{CO2}(g)\)
4. \(\ce{CaCO}(s)⟶\ce{CaO}(s)+\ce{CO2}(g)\)

Contestar a

Positivo; El sólido se disuelve para dar un aumento de iones móviles en solución.

Respuesta b

Negativo; El líquido se convierte en un sólido más ordenado.

Respuesta c

Positivo; El sólido relativamente ordenado se convierte en un gas

Respuesta d

Positivo; Hay una producción neta de un mol de gas.

Resumen

La entropía (\(S\)) es una función de estado que puede estar relacionada con el número de microestados para un sistema (el número de formas en que se puede organizar el sistema) y con la relación entre el calor reversible y la temperatura Kelvin. Se puede interpretar como una medida de la dispersión o distribución de materia y/o energía en un sistema, y a menudo se describe como que representa el “desorden” del sistema. Para una sustancia dada,\(S_{solid} < S_{liquid} \ll S_{gas}\) en un estado físico dado a una temperatura dada, la entropía es típicamente mayor para átomos más pesados o moléculas más complejas. La entropía aumenta cuando se calienta un sistema y cuando se forman soluciones. Usando estas pautas, el signo de cambios de entropía para algunas reacciones químicas puede predecirse de manera confiable.

Ecuaciones Clave

• \(ΔS=\dfrac{q_\ce{rev}}{T}\)
• S = k ln W
• \(ΔS=k\ln\dfrac{W_\ce{f}}{W_\ce{i}}\)

Glosario

entropía (S)

función de estado que es una medida de la materia y/o dispersión de energía dentro de un sistema, determinada por el número de microestados del sistema que a menudo se describen como una medida del trastorno del sistema

microestado (W)

posible configuración o disposición de materia y energía dentro de un sistema

proceso reversible

proceso que tiene lugar tan lentamente como para ser capaz de invertir dirección en respuesta a un cambio infinitesimalmente pequeño en las condiciones; construcción hipotética que solo puede ser aproximada por procesos reales removidos