21.3: Desintegración radiactiva
- Page ID
- 75732
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Reconocer modos comunes de desintegración radiactiva
- Identificar partículas y energías comunes involucradas en reacciones de desintegración nuclear
- Escribir y equilibrar ecuaciones de desintegración nuclear
- Calcular parámetros cinéticos para procesos de descomposición, incluida la vida media
- Describir técnicas comunes de datación radiométrica
Tras el descubrimiento algo fortuito de la radiactividad por Becquerel, muchos científicos destacados comenzaron a investigar este nuevo e intrigante fenómeno. Entre ellas se encontraban Marie Curie (la primera mujer en ganar un Premio Nobel, y la única persona en ganar dos Premios Nobel en diferentes ciencias: química y física), quien fue la primera en acuñar el término “radiactividad”, y Ernest Rutherford (de fama de experimento de lámina de oro), quien investigó y nombró a tres de los más comunes tipos de radiación. A principios del siglo XX se descubrieron muchas sustancias radiactivas, se investigaron y cuantificaron las propiedades de la radiación y se desarrolló una sólida comprensión de la radiación y la desintegración nuclear.
El cambio espontáneo de un nucleido inestable a otro es la desintegración radiactiva. El nucleido inestable se llama el nucleido padre; el nucleido que resulta de la decadencia se conoce como el nucleido hijo. El nucleido hijo puede ser estable, o puede decaer por sí mismo. La radiación producida durante la desintegración radiactiva es tal que el núclido hijo se encuentra más cerca de la banda de estabilidad que el núclido progenitor, por lo que la ubicación de un núclido con relación a la banda de estabilidad puede servir de guía para el tipo de descomposición que sufrirá (Figura\(\PageIndex{1}\)).
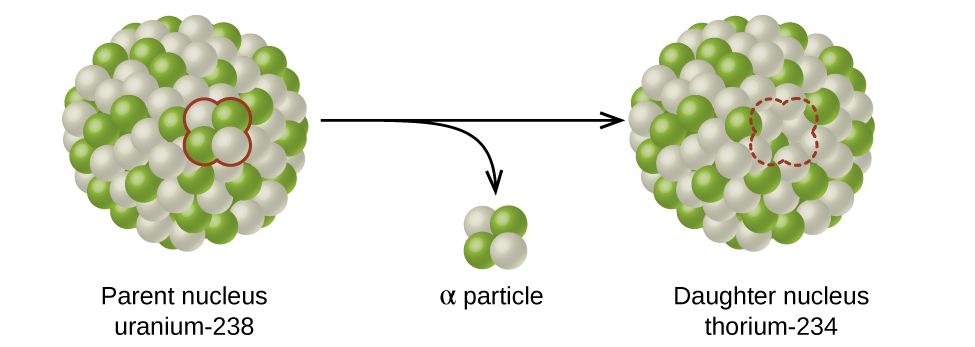
Aunque la desintegración radiactiva de un núcleo es demasiado pequeña para verla a simple vista, podemos ver indirectamente la desintegración radiactiva en un ambiente llamado cámara de nubes. Da clic aquí para conocer las cámaras de nubes y ver una interesante Demostración de Cámara Nube del Jefferson Lab.
Tipos de desintegración radiactiva
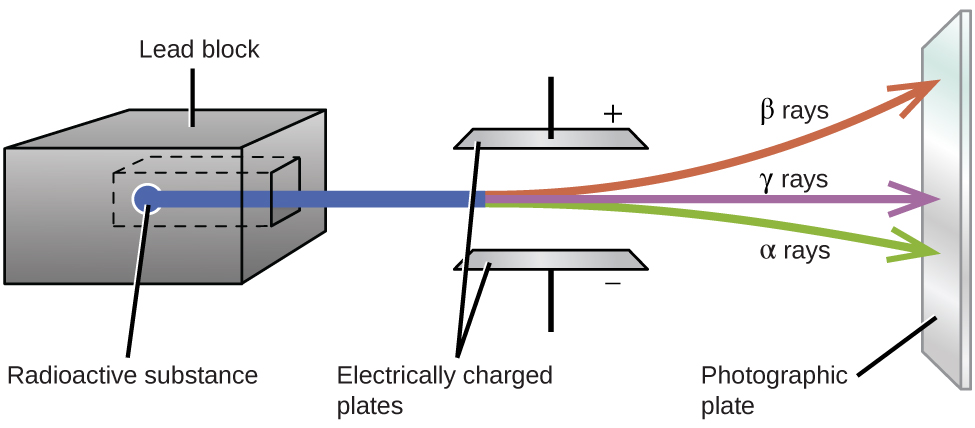
Los experimentos de Ernest Rutherford que involucraron la interacción de la radiación con un campo magnético o eléctrico (Figura\(\PageIndex{2}\)) le ayudaron a determinar que un tipo de radiación consistía en\(α\) partículas cargadas positivamente y relativamente masivas; un segundo tipo estaba compuesto por carga negativa y mucho menos \(β\)partículas masivas; y un tercero fue ondas electromagnéticas sin carga,\(γ\) rayos. Ahora sabemos que\(α\) las partículas son núcleos de helio de alta energía,\(β\) las partículas son electrones de alta energía y la\(γ\) radiación compone radiación electromagnética de alta energía. Clasificamos diferentes tipos de desintegración radiactiva por la radiación producida.
Alfa (\(α\)) decayes la emisión de una partícula α desde el núcleo. Por ejemplo, el polonio-210 sufre una desintegración α:
\[\ce{^{210}_{84}Po⟶ ^4_2He + ^{206}_{82}Pb} \hspace{40px}\ce{or}\hspace{40px} \ce{^{210}_{84}Po ⟶ ^4_2α + ^{206}_{82}Pb}\nonumber \]
La desintegración alfa ocurre principalmente en núcleos pesados (A > 200, Z > 83). Debido a que la pérdida de una partícula α da un nucleido hijo con un número de masa cuatro unidades más pequeño y un número atómico dos unidades más pequeñas que las del nucleido padre, el nucleido hijo tiene una relación n:p mayor que el nucleido padre. Si el nucleido progenitor que sufre decaimiento α se encuentra por debajo de la banda de estabilidad, el nucleido hijo estará más cerca de la banda.
La desintegración beta (β) es la emisión de un electrón desde un núcleo. El yodo-131 es un ejemplo de un nucleido que sufre una desintegración β:
\[\ce{^{131}_{53}I ⟶ ^0_{-1}e + ^{131}_{54}X} \hspace{40px}\ce{or}\hspace{40px} \ce{^{131}_{53}I ⟶ ^0_{-1}β + ^{131}_{54}Xe}\nonumber \]
La desintegración beta, que puede considerarse como la conversión de un neutrón en protón y una partícula β, se observa en nucleidos con una gran relación n:p. La partícula beta (electrón) emitida es del núcleo atómico y no es uno de los electrones que rodean el núcleo. Dichos núcleos se encuentran por encima de la banda de estabilidad. La emisión de un electrón no cambia el número de masa del nucleido pero sí aumenta el número de sus protones y disminuye el número de sus neutrones. En consecuencia, la relación n:p disminuye, y el nucleido hijo se encuentra más cerca de la banda de estabilidad que el nucleido progenitor.
La emisión gamma (emisión γ) se observa cuando se forma un nucleido en estado excitado y luego decae a su estado fundamental con la emisión de un rayo γ, un cuántico de radiación electromagnética de alta energía. La presencia de un núcleo en estado excitado a menudo se indica con un asterisco (*). El cobalto-60 emite radiación γ y se utiliza en muchas aplicaciones, incluyendo el tratamiento del cáncer:
\[\mathrm{^{60}_{27}Co^* ⟶\, ^0_0γ +\, ^{60}_{27}Co}\nonumber \]
No hay cambio en el número de masa o número atómico durante la emisión de un rayo γ a menos que la emisión γ acompañe a uno de los otros modos de decaimiento.
El ion positrón emiss (\(β^+\)decaimiento) es la emisión de un positrón desde el núcleo. Oxígeno-15 es un ejemplo de un nucleido que sufre emisión de positrones:
\[\ce{^{15}_8O ⟶ ^0_{+1}e + ^{15}_7N} \hspace{40px}\ce{or}\hspace{40px} \ce{^{15}_8O ⟶ ^0_{+1}β + ^{15}_7N}\nonumber \]
La emisión de positrones se observa para nucleidos en los que la relación n:p es baja. Estos nucleidos se encuentran por debajo de la banda de estabilidad. La desintegración de positrones es la conversión de un protón en un neutrón con la emisión de un positrón. La relación n:p aumenta, y el nucleido hijo se encuentra más cerca de la banda de estabilidad que el nucleido padre.
La captura de electrones ocurre cuando uno de los electrones internos de un átomo es capturado por el núcleo del átomo. Por ejemplo, el potasio-40 se somete a captura de electrones:
\[\ce{^{40}_{19}K + ^0_{-1}e ⟶ ^{40}_{18}Ar}\nonumber \]
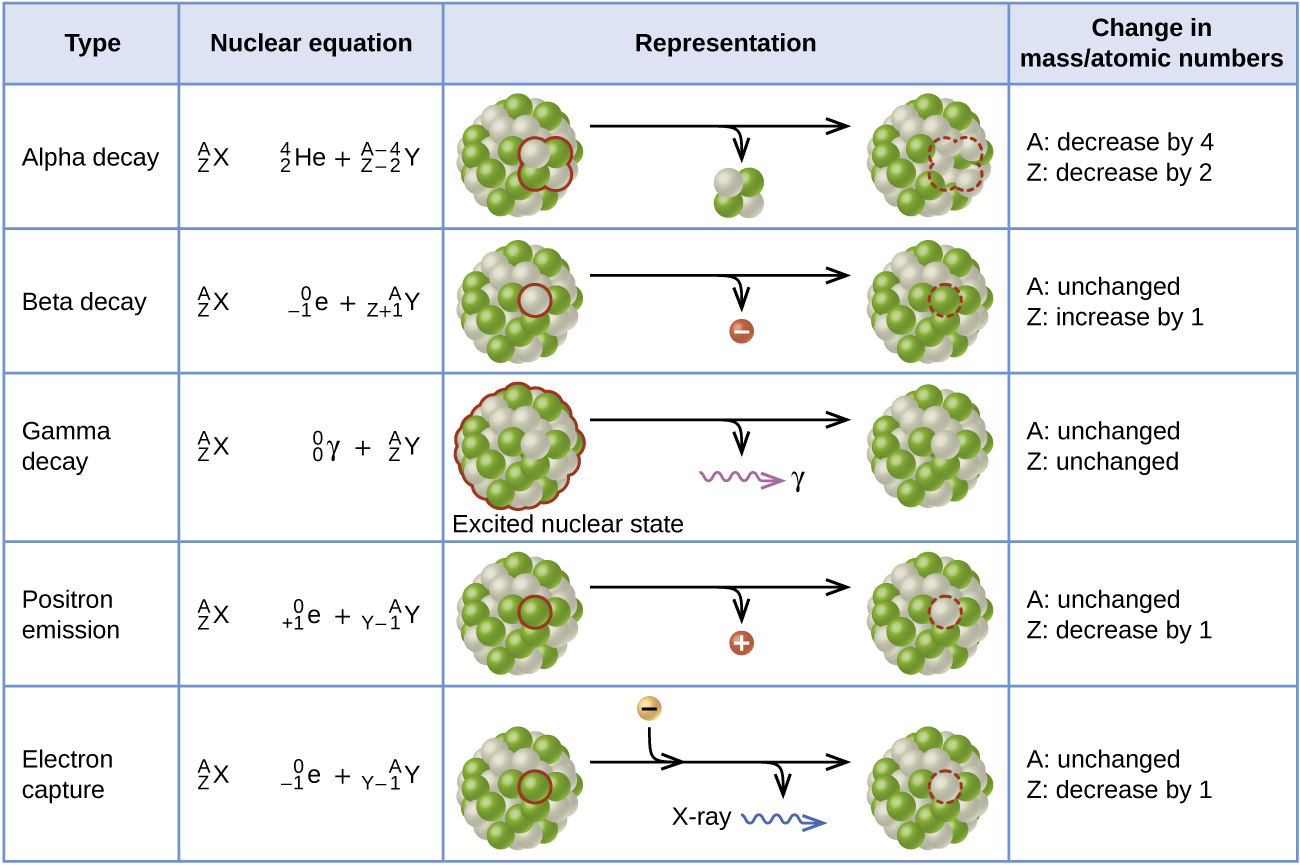
La captura de electrones ocurre cuando un electrón de capa interna se combina con un protón y se convierte en un neutrón. La pérdida de un electrón de capa interna deja una vacante que será llenada por uno de los electrones externos. A medida que el electrón exterior cae en la vacante, emitirá energía. En la mayoría de los casos, la energía emitida será en forma de rayos X. Al igual que la emisión de positrones, la captura de electrones ocurre para núcleos “ricos en protones” que se encuentran por debajo de la banda de estabilidad. La captura de electrones tiene el mismo efecto en el núcleo que la emisión de positrones: El número atómico disminuye en uno y el número de masa no cambia. Esto aumenta la relación n:p, y el nucleido hijo se encuentra más cerca de la banda de estabilidad que el nucleido padre. Es difícil predecir si se produce la captura de electrones o la emisión de positrones. La elección se debe principalmente a factores cinéticos, siendo el que requiere la energía de activación más pequeña el que tiene más probabilidades de ocurrir. La figura\(\PageIndex{3}\) resume estos tipos de decaimiento, junto con sus ecuaciones y cambios en los números atómicos y másticos.
Las tomografías por emisión de positrones (PET) utilizan radiación para diagnosticar y rastrear afecciones de salud y monitorear los tratamientos médicos al revelar cómo funcionan las partes del cuerpo de un paciente (Figura\(\PageIndex{4}\)). Para realizar una exploración por PET, se produce un radioisótopo emisor de positrones en un ciclotrón y luego se une a una sustancia que es utilizada por la parte del cuerpo que se investiga. Este compuesto “etiquetado”, o radiotrazador, se introduce luego en el paciente (inyectado vía IV o se respira como un gas), y cómo es utilizado por el tejido revela cómo funciona ese órgano u otra área del cuerpo.
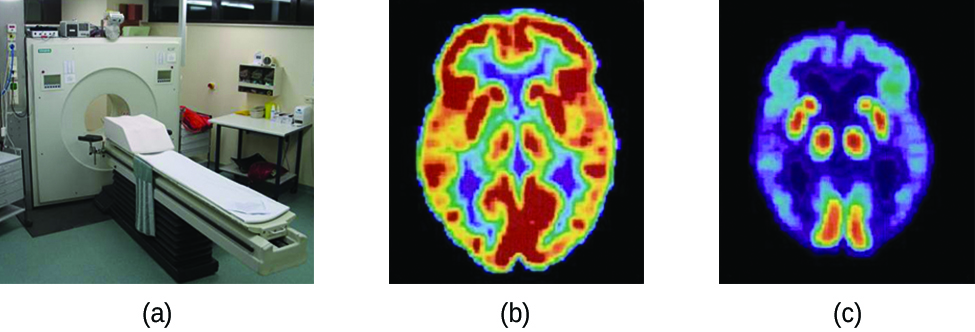
Por ejemplo, F-18 es producido por bombardeo de protones de 18 O\( (\ce{^{18}_8O + ^1_1p⟶ ^{18}_9F + ^1_0n})\) e incorporado a un análogo de glucosa llamado fludesoxiglucosa (FDG). La forma en que el cuerpo usa FDG proporciona información diagnóstica crítica; por ejemplo, dado que los cánceres usan la glucosa de manera diferente a los tejidos normales, FDG puede revelar cánceres. El 18 F emite positrones que interactúan con electrones cercanos, produciendo una ráfaga de radiación gamma. Esta energía es detectada por el escáner y convertida en una imagen detallada, tridimensional, a color que muestra cómo funciona esa parte del cuerpo del paciente. Diferentes niveles de radiación gamma producen diferentes cantidades de brillo y colores en la imagen, que luego pueden ser interpretados por un radiólogo para revelar lo que está sucediendo. Las TEP pueden detectar daño cardíaco y enfermedades cardíacas, ayudar a diagnosticar la enfermedad de Alzheimer, indicar la parte de un cerebro que se ve afectada por la epilepsia, revelar cáncer, mostrar en qué etapa se encuentra y cuánto se ha diseminado, y si los tratamientos son efectivos. A diferencia de las imágenes por resonancia magnética y los rayos X, que solo muestran cómo se ve algo, la gran ventaja de las exploraciones PET es que muestran cómo funciona algo. Las exploraciones por TEP ahora generalmente se realizan junto con una tomografía computarizada.
Serie de desintegración radiactiva
Los isótopos radiactivos naturales de los elementos más pesados caen en cadenas de desintegraciones sucesivas., o decae, y todas las especies en una cadena constituyen una familia radiactiva, o serie de desintegración radiactiva. Tres de estas series incluyen la mayoría de los elementos radiactivos naturalmente de la tabla periódica. Son la serie de uranio, la serie de actínidos y la serie de torio. La serie neptunium es una cuarta serie, que ya no es significativa en la tierra debido a la corta vida media de las especies involucradas. Cada serie se caracteriza por un padre (primer miembro) que tiene una vida media larga y una serie de nucleidos hijos que finalmente conducen a un producto final estable, es decir, un nucleido en la banda de estabilidad (Figura\(\PageIndex{5}\)). En las tres series, el producto final es un isótopo estable de plomo. La serie de neptunio, previamente pensada para terminar con bismuto-209, termina con talio-205.
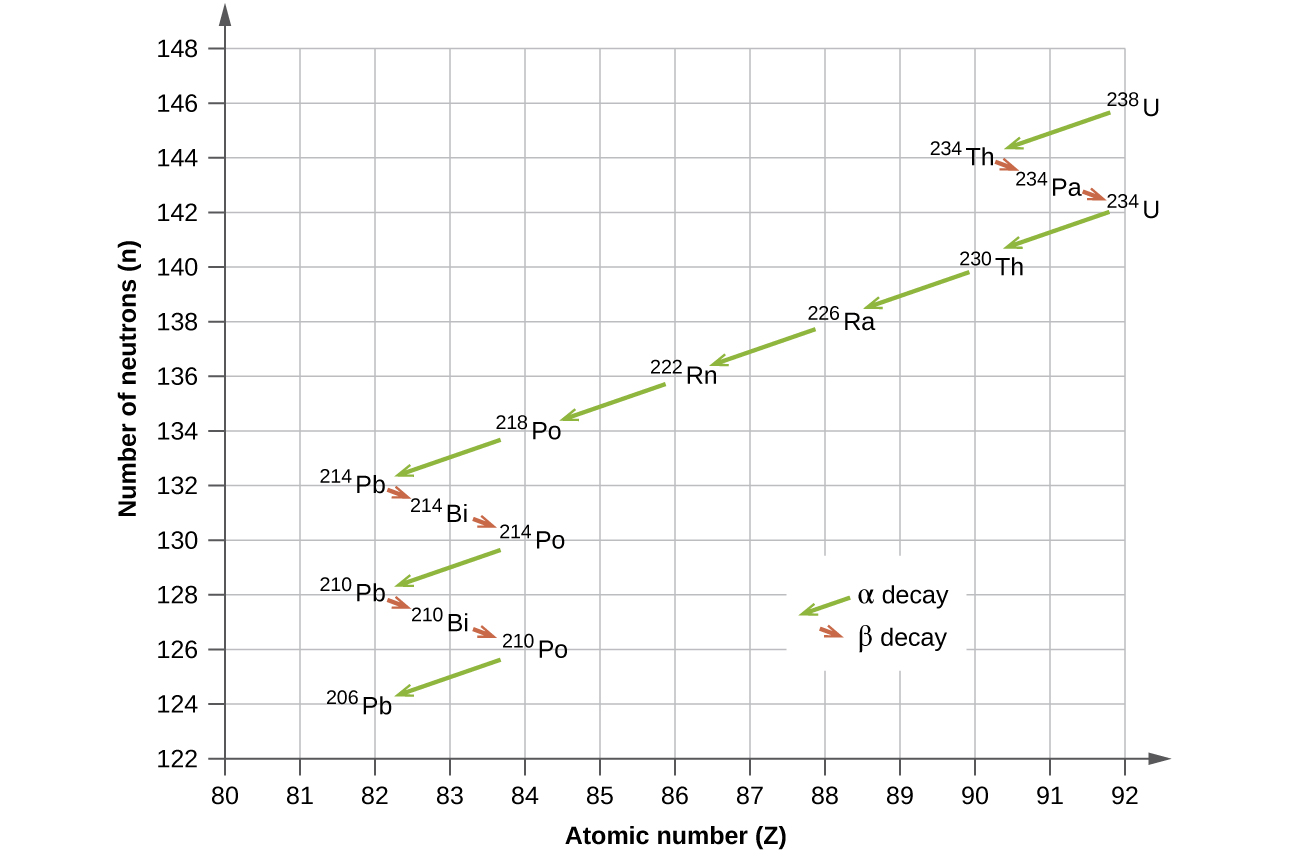
Semividas radiactivas
La desintegración radiactiva sigue la cinética de primer orden. Dado que las reacciones de primer orden ya se han cubierto en detalle en el capítulo de cinética, ahora aplicaremos esos conceptos a las reacciones de desintegración nuclear. Cada nucleido radiactivo tiene una vida media característica constante (t 1/2), el tiempo requerido para que la mitad de los átomos en una muestra se descomponga. La vida media de un isótopo nos permite determinar cuánto tiempo estará disponible una muestra de un isótopo útil y cuánto tiempo debe almacenarse una muestra de un isótopo indeseable o peligroso antes de que descomponga a un nivel de radiación lo suficientemente bajo que ya no es un problema.
Por ejemplo, el cobalto-60, isótopo que emite rayos gamma utilizados para tratar el cáncer, tiene una vida media de 5.27 años (Figura\(\PageIndex{6}\)). En una fuente dada de cobalto-60, dado que la mitad de los\(\ce{^{60}_{27}Co}\) núcleos se descomponen cada 5.27 años, tanto la cantidad de material como la intensidad de la radiación emitida se cortan a la mitad cada 5.27 años. (Obsérvese que para una sustancia dada, la intensidad de radiación que produce es directamente proporcional a la tasa de descomposición de la sustancia y la cantidad de la sustancia.) Esto es como se esperaba para un proceso que sigue la cinética de primer orden. Por lo tanto, una fuente de cobalto-60 que se utiliza para el tratamiento del cáncer debe ser reemplazada regularmente para seguir siendo efectiva.

Dado que la desintegración nuclear sigue una cinética de primer orden, podemos adaptar las relaciones matemáticas utilizadas para las reacciones químicas de primer orden. Generalmente sustituimos el número de núcleos, N, por la concentración. Si la tasa se expresa en desintegraciones nucleares por segundo, nos referimos a ella como la actividad de la muestra radiactiva. La tasa de desintegración radiactiva es:
\[\text{decay rate} = \lambda N\nonumber \]
con\(\lambda\) es la constante de desintegración para el radioisótopo particular.
La constante de decaimiento\(\lambda\), que es la misma que una constante de velocidad discutida en el capítulo de cinética. Es posible expresar la constante de decaimiento en términos de la vida media, t 1/2:
\[λ=\dfrac{\ln 2}{t_{1/2}}=\dfrac{0.693}{t_{1/2}} \hspace{40px}\ce{or}\hspace{40px} t_{1/2}=\dfrac{\ln 2}{λ}=\dfrac{0.693}{λ}\nonumber \]
Las ecuaciones de primer orden que relacionan cantidad, N y tiempo son:
\[N_t=N_0e^{−kt} \hspace{40px}\ce{or}\hspace{40px} t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)\nonumber \]
donde N 0 es el número inicial de núcleos o moles del isótopo, y N t es el número de núcleos/moles que quedan en el tiempo t. Ejemplo\(\PageIndex{1}\) aplica estos cálculos para encontrar las tasas de desintegración radiactiva para nucleidos específicos.
\(\ce{^{60}_{27}Co}\)decae con una vida media de 5.27 años para producir\(\ce{^{60}_{28}Ni}\).
- ¿Cuál es la constante de desintegración para la desintegración radiactiva del cobalto-60?
- Calcular la fracción de una muestra del\(\ce{^{60}_{27}Co}\) isótopo que quedará después de 15 años.
- ¿Cuánto tiempo tarda una muestra de\(\ce{^{60}_{27}Co}\) en desintegrarse en la medida en que sólo queda 2.0% de la cantidad original?
Solución
a) El valor de la constante de tasa viene dado por:
\[λ=\dfrac{\ln 2}{t_{1/2}}=\mathrm{\dfrac{0.693}{5.27\:y}=0.132\:y^{−1}} \nonumber \]
b) La fracción de\(\ce{^{60}_{27}Co}\) eso queda después de que el tiempo t sea dado por\(\dfrac{N_t}{N_0}\). Reorganizar la relación de primer orden N t = N 0 e — λt para resolver para esta relación rinde:
\[\dfrac{N_t}{N_0}=e^{-λt}=e^\mathrm{-(0.132/y)(15.0/y)}=0.138 \nonumber \]
La fracción de\(\ce{^{60}_{27}Co}\) eso se mantendrá después de 15.0 años es 0.138. O dicho de otra manera, 13.8% de los\(\ce{^{60}_{27}Co}\) originalmente presentes quedarán después de 15 años.
(c) 2.00% de la cantidad original de\(\ce{^{60}_{27}Co}\) es igual a 0.0200 × N 0. Sustituyendo esto en la ecuación por tiempo para la cinética de primer orden, tenemos:
\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)=−\dfrac{1}{0.132\:\ce y^{−1}}\ln\left(\dfrac{0.0200×N_0}{N_0}\right)=29.6\:\ce y \nonumber \]
El radón-222,\(\ce{^{222}_{86}Rn}\), tiene una vida media de 3.823 días. ¿Cuánto tiempo tardará una muestra de radón-222 con una masa de 0.750 g para descomponerse en otros elementos, dejando solo 0.100 g de radón-222?
- Responder
-
11.1 días
Debido a que cada nucleido tiene un número específico de nucleones, un equilibrio particular de repulsión y atracción, y su propio grado de estabilidad, las vidas medias de los nucleidos radiactivos varían ampliamente. Por ejemplo: la vida media de\(\ce{^{209}_{83}Bi}\) es 1.9 × 10 19 años;\(\ce{^{239}_{94}Ra}\) es 24,000 años;\(\ce{^{222}_{86}Rn}\) es 3.82 días; y elemente-111 (Rg para roentgenium) es 1.5 × 10 —3 segundos. Las vidas medias de una serie de isótopos radiactivos importantes para la medicina se muestran en la Tabla\(\PageIndex{1}\), y otros se enumeran en el Apéndice N1.
| Tipo | Modo Decaimiento | Vida media | Usos |
|---|---|---|---|
| F-18 | β + decaimiento | 110. minutos | Escaneos PET |
| Co-60 | β decaimiento, γ decaimiento | 5.27 años | tratamiento del cáncer |
| Tc-99m 1 | decaimiento γ | 8.01 horas | exploraciones de cerebro, pulmón, corazón, hueso |
| I-131 | β decaimiento | 8.02 días | exploraciones tiroideas y tratamiento |
| Tl-201 | captura de electrones | 73 horas | exploraciones cardíacas y arteriales; pruebas de esfuerzo cardíaco |
| La “m” en Tc-99m significa “metaestable”, lo que indica que se trata de un estado inestable y de alta energía de Tc-99. Los isótopos metaestables emiten\(γ\) radiación para deshacerse del exceso de energía y volverse (más) estables. | |||
Datación radiométrica
Varios radioisótopos tienen semividas y otras propiedades que los hacen útiles con fines de “fechar” el origen de objetos como artefactos arqueológicos, anteriormente organismos vivos o formaciones geológicas. Este proceso es radiométrico y ha sido responsable de muchos descubrimientos científicos innovadores sobre la historia geológica de la tierra, la evolución de la vida y la historia de la civilización humana. Exploraremos algunos de los tipos más comunes de datación radiactiva y cómo funcionan los isótopos particulares para cada tipo.
Datación radiactiva usando carbono-14
La radiactividad del carbono-14 proporciona un método para fechar objetos que formaban parte de un organismo vivo. Este método de datación radiométrica, que también se llama datación por radiocarbono o datación por carbono-14, es preciso para fechar sustancias que contienen carbono que tienen hasta aproximadamente 30,000 años de antigüedad, y puede proporcionar fechas razonablemente precisas hasta un máximo de aproximadamente 50,000 años de antigüedad.
El carbono natural consta de tres isótopos:\(\ce{^{12}_6C}\), que constituye aproximadamente 99% del carbono en la tierra;\(\ce{^{13}_6C}\), aproximadamente 1% del total; y trazas de\(\ce{^{14}_6C}\). El carbono-14 se forma en la atmósfera superior por la reacción de los átomos de nitrógeno con los neutrones de los rayos cósmicos en el espacio:
\[\ce{^{14}_7N + ^1_0n⟶ ^{14}_6C + ^1_1H}\nonumber \]
Todos los isótopos de carbono reaccionan con el oxígeno para producir moléculas de CO 2. La relación de\(\ce{^{14}_6CO2}\) a\(\ce{^{12}_6CO2}\) depende de la relación de\(\ce{^{14}_6CO}\) a\(\ce{^{12}_6CO}\) en la atmósfera. La abundancia natural\(\ce{^{14}_6CO}\) en la atmósfera es de aproximadamente 1 parte por billón; hasta hace poco, esto ha sido generalmente constante a lo largo del tiempo, ya que se ven muestras de gas que se encuentran atrapadas en el hielo. La incorporación de\(\ce{^{14}_6C ^{14}_6CO2}\) y\(\ce{^{12}_6CO2}\) dentro de las plantas es una parte regular del proceso de fotosíntesis, lo que significa que la\(\ce{^{14}_6C: ^{12}_6C}\) proporción que se encuentra en una planta viva es la misma que la\(\ce{^{14}_6C: ^{12}_6C}\) proporción en la atmósfera. Pero cuando la planta muere, ya no atrapa carbono a través de la fotosíntesis. Debido a que\(\ce{^{12}_6C}\) es un isótopo estable y no sufre desintegración radiactiva, su concentración en la planta no cambia. Sin embargo, el carbono-14 decae por emisión β con una vida media de 5730 años:
\[\ce{^{14}_6C⟶ ^{14}_7N + ^0_{-1}e}\nonumber \]
Así, la\(\ce{^{14}_6C: ^{12}_6C}\) proporción disminuye gradualmente después de la muerte de la planta. La disminución en la relación con el tiempo proporciona una medida del tiempo que ha transcurrido desde la muerte de la planta (u otro organismo que se comió la planta). La figura representa\(\PageIndex{7}\) visualmente este proceso.
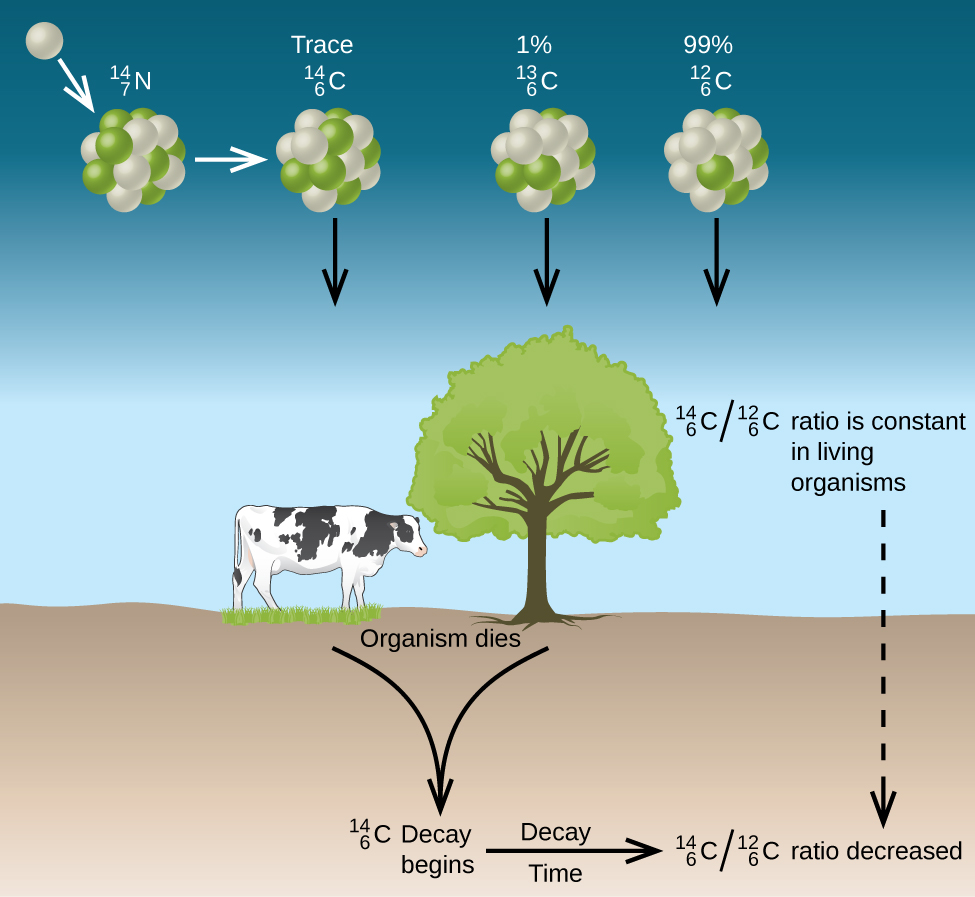
Por ejemplo, con la vida media de\(\ce{^{14}_6C}\) ser de 5730 años, si la\(\ce{^{14}_6C : ^{12}_6C}\) proporción en un objeto de madera que se encuentra en una excavación arqueológica es la mitad de lo que es en un árbol vivo, esto indica que el objeto de madera tiene 5730 años de antigüedad. Se pueden obtener determinaciones de\(\ce{^{14}_6C : ^{12}_6C}\) proporciones de alta precisión a partir de muestras muy pequeñas (tan solo un miligramo) mediante el uso de un espectrómetro de masas.
Un pequeño trozo de papel (producido a partir de materia vegetal anteriormente viva) tomado de los Rollos del Mar Muerto tiene una actividad de 10.8 desintegraciones por minuto por gramo de carbono. Si la actividad inicial de C-14 fue de 13.6 desintegraciones/min/g de C, estime la edad de los Rollos del Mar Muerto.
Solución
La tasa de desintegración (número de desintegraciones/minuto/gramo de carbono) es proporcional a la cantidad de C-14 radiactivo que queda en el papel, por lo que podemos sustituir las tasas por las cantidades, N, en la relación:
\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)⟶t=−\dfrac{1}{λ}\ln\left(\dfrac{\ce{Rate}_t}{\ce{Rate}_0}\right) \nonumber \]
donde el subíndice 0 representa el tiempo en que se cortaron las plantas para hacer el papel, y el subíndice t representa el tiempo actual.
La constante de decaimiento se puede determinar a partir de la semivida de C-14, 5730 años:
\[λ=\dfrac{\ln 2}{t_{1/2}}=\mathrm{\dfrac{0.693}{5730\: y}=1.21×10^{−4}\:y^{−1}} \nonumber \]
Sustituyendo y resolviendo, contamos con:
\[t=−\dfrac{1}{λ}\ln\left(\dfrac{\ce{Rate}_t}{\ce{Rate}_0}\right)=\mathrm{−\dfrac{1}{1.21×10^{−4}\:y^{−1}}\ln\left(\dfrac{10.8\:dis/min/g\: C}{13.6\:dis/min/g\: C}\right)=1910\: y}\nonumber \]
Por lo tanto, los Rollos del Mar Muerto tienen aproximadamente 1900 años de antigüedad (Figura\(\PageIndex{8}\)).

Recientemente se han determinado fechas más precisas de los reinados de los antiguos faraones egipcios utilizando plantas que se conservaron en sus tumbas. Muestras de semillas y materia vegetal de la tumba del rey Tutankamón tienen una tasa de desintegración C-14 de 9.07 desintegraciones/min/g de C. ¿Cuánto tiempo hace que el reinado del rey Tut llegó a su fin?
- Responder
-
hace cerca de 3350 años, o aproximadamente 1340 a.C.
Se han producido algunos cambios significativos y bien documentados en la\(\ce{^{14}_6C : ^{12}_6C}\) relación. La precisión de una aplicación directa de esta técnica depende de que la\(\ce{^{14}_6C : ^{12}_6C}\) proporción en una planta viva sea la misma ahora que en una época anterior, pero esto no siempre es válido. Debido a la creciente acumulación de moléculas de CO 2 (en gran parte\(\ce{^{12}_6CO2}\)) en la atmósfera causada por la combustión de combustibles fósiles (en los que esencialmente todo el\(\ce{^{14}_6C}\) ha decaído), la relación de\(\ce{^{14}_6C : ^{12}_6C}\) en la atmósfera puede estar cambiando. Este aumento provocado por el hombre\(\ce{^{12}_6CO2}\) en la atmósfera hace que la\(\ce{^{14}_6C : ^{12}_6C}\) proporción disminuya, y esto a su vez afecta la proporción en los organismos actualmente vivos en la tierra. Afortunadamente, sin embargo, podemos utilizar otros datos, como la datación de árboles mediante el examen de anillos de crecimiento anuales, para calcular los factores de corrección. Con estos factores de corrección se pueden determinar fechas exactas. En general, la datación radiactiva solo funciona durante aproximadamente 10 semividas; por lo tanto, el límite para la datación por carbono-14 es de unos 57 mil años.
Datación radiactiva mediante nucleidos distintos del carbono-14
La datación radiactiva también puede utilizar otros nucleidos radiactivos con vidas medias más largas para fechar eventos más antiguos. Por ejemplo, el uranio-238 (que decae en una serie de escalones en plomo-206) se puede utilizar para establecer la edad de las rocas (y la edad aproximada de las rocas más antiguas de la tierra). Dado que el U-238 tiene una vida media de 4.5 mil millones de años, la mitad del U-238 original tarda esa cantidad de tiempo en descomponerse en Pb-206. En una muestra de roca que no contiene cantidades apreciables de Pb-208, el isótopo de plomo más abundante, podemos suponer que el plomo no estaba presente cuando se formó la roca. Por lo tanto, midiendo y analizando la relación de U-238:Pb-206, podemos determinar la edad de la roca. Esto supone que todo el plomo-206 presente vino de la descomposición del uranio-238. Si hay plomo-206 adicional presente, lo que se indica por la presencia de otros isótopos de plomo en la muestra, es necesario hacer un ajuste. Potasio-argón La datación utiliza un método similar. K-40 decae por emisión de positrones y captura de electrones para formar Ar-40 con una vida media de 1.25 mil millones de años. Si se tritura una muestra de roca y se mide la cantidad de gas Ar-40 que escapa, la determinación de la relación Ar-40:K-40 produce la edad de la roca. Otros métodos, como la datación rubidio-estroncio (Rb-87 decae en Sr-87 con una vida media de 48.800 millones de años), operan bajo el mismo principio. Para estimar el límite inferior para la edad de la tierra, los científicos determinan la edad de diversas rocas y minerales, asumiendo que la tierra es más antigua que las rocas y minerales más antiguos de su corteza. A partir de 2014, las rocas más antiguas conocidas en la tierra son los circones Jack Hills de Australia, encontrados por uranio-plomo que datan de casi 4.4 mil millones de años.
Una roca ígnea contiene 9.58 × 10 —5 g de U-238 y 2.51 × 10 —5 g de Pb-206, y cantidades mucho, mucho menores de Pb-208. Determinar el tiempo aproximado en el que se formó la roca.
Solución
La muestra de roca contiene muy poco Pb-208, el isótopo más común de plomo, por lo que podemos suponer con seguridad que todo el Pb-206 en la roca fue producido por la desintegración radiactiva de U-238. Cuando se formó la roca, contenía todo el U-238 actualmente en ella, más algunos U-238 que desde entonces han sufrido desintegración radiactiva.
La cantidad de U-238 actualmente en la roca es:
\[\mathrm{9.58×10^{−5}\cancel{g\: U}×\left( \dfrac{1\: mol\: U}{238\cancel{g\: U}}\right )=4.03×10^{−7}\:mol\: U}\nonumber \]
Porque cuando un mol de U-238 decae, produce un mol de Pb-206, la cantidad de U-238 que ha sufrido desintegración radiactiva desde que se formó la roca es:
\[\mathrm{2.51×10^{-5}\cancel{g\: Pb}×\left( \dfrac{1\cancel{mol\: Pb}}{206\cancel{g\: Pb}}\right )×\left(\dfrac{1\: mol\: U}{1\cancel{mol\: Pb}}\right)=1.22×10^{-7}\:mol\: U}\nonumber \]
La cantidad total de U-238 originalmente presente en la roca es por lo tanto:
\[\mathrm{4.03×10^{−7}\:mol+1.22×10^{−7}\:mol=5.25×10^{−7}\:mol\: U}\nonumber \]La cantidad de tiempo que ha pasado desde la formación de la roca viene dada por:
\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)\nonumber \]con N 0 representando la cantidad original de U-238 y N t representando la cantidad actual de U-238.
U-238 decae en Pb-206 con una semivida de 4.5 × 10 9 y, por lo que la constante de decaimiento λ es:
\[t=\mathrm{−\dfrac{1}{1.54×10^{−10}\:y^{−1}}\ln\left(\dfrac{4.03×10^{−7}\cancel{mol\: U}}{5.25×10^{−7}\cancel{mol\: U}}\right)=1.7×10^9\:y}\nonumber \]
Por lo tanto, la roca tiene aproximadamente 1.7 mil millones de años.
Una muestra de roca contiene 6.14 × 10 —4 g de Rb-87 y 3.51 × 10 —5 g de Sr-87. Calcular la edad de la roca. (La vida media de la desintegración β de Rb-87 es 4.7 × 10 10 y.)
- Responder
-
3.7 × 10 9 y
Resumen
Los núcleos que tienen relaciones n:p inestables experimentan desintegración radiactiva espontánea. Los tipos más comunes de radiactividad son la desintegración α, la desintegración β, la emisión γ, la emisión de positrones y la captura de electrones. Las reacciones nucleares también suelen involucrar rayos γ, y algunos núcleos se descomponen por captura de electrones. Cada uno de estos modos de descomposición conduce a la formación de un nuevo núcleo con una relación n:p más estable. Algunas sustancias sufren series de desintegración radiactiva, procediendo a través de múltiples desintegraciones antes de terminar en un isótopo estable. Todos los procesos de desintegración nuclear siguen una cinética de primer orden., y cada radioisótopo tiene su propia vida media característica, el tiempo que se requiere para que la mitad de sus átomos se descomponga. Debido a las grandes diferencias en la estabilidad entre los nucleidos, existe una gama muy amplia de semividas de sustancias radiactivas. Muchas de estas sustancias han encontrado aplicaciones útiles en el diagnóstico y tratamiento médico, determinando la edad de los objetos arqueológicos y geológicos, y más.
Ecuaciones Clave
- tasa de decaimiento = λN
- \(t_{1/2}=\dfrac{\ln 2}{λ}=\dfrac{0.693}{λ}\)
Glosario
- desintegración alfa (α)
- pérdida de una partícula alfa durante la desintegración radiactiva
- decaimiento beta (β)
- descomposición de un neutrón en un protón, que permanece en el núcleo, y un electrón, que se emite como una partícula beta
- nuclide hija
- nucleido producido por la desintegración radiactiva de otro nucleido; puede ser estable o puede desintegrarse aún más
- captura de electrones
- combinación de un electrón central con un protón para producir un neutrón dentro del núcleo
- emisión gamma (γ)
- decaimiento de un nucleido en estado excitado acompañado de emisión de un rayo gamma
- vida media (t 1/2)
- tiempo requerido para que la mitad de los átomos de una muestra radiactiva se desintegren
- Nuclido padre
- nucleido inestable que cambia espontáneamente en otro nucleido (hija)
- emisión de positrones
- (también, β + decaimiento) conversión de un protón en un neutrón, que permanece en el núcleo, y un positrón, que se emite
- desintegración radiactiva
- descomposición espontánea de un nucleido inestable en otro nucleido
- serie de desintegración radiactiva
- cadenas de desintegraciones sucesivas (desintegraciones radiactivas) que finalmente conducen a un producto final estable
- datación por radiocarbono
- medios altamente precisos de fechar objetos de 30,000—50,000 años de antigüedad que se derivaron de la materia que alguna vez estuvo; lograda calculando la proporción de\(\ce{^{14}_6C : ^{12}_6C}\) en el objeto vs. la relación de\(\ce{^{14}_6C : ^{12}_6C}\) en la atmósfera actual
- datación radiométrica
- uso de radioisótopos y sus propiedades para fechar la formación de objetos como artefactos arqueológicos, organismos anteriormente vivos o formaciones geológicas


