4.3: Potenciales electroquímicos

En celdas electroquímicas, o en reacciones redox que ocurren en solución, la fuerza motriz termodinámica se puede medir como el potencial celular. Las reacciones químicas son espontáneas en la dirección de -ΔG, que es también la dirección en la que el potencial celular (definido como _cátodo E - _ánodo E) es positivo. Una celda que opera en la dirección espontánea (por ejemplo, una batería que se está descargando) se llama celda galvánica. Una celda que se está impulsando en la dirección no espontánea se llama celda electrolítica. Por ejemplo, consideremos la reacción del hidrógeno y el oxígeno para hacer agua:

\[\ce{2H2_{(g)} + O2_{(g)} = 2H2O_{(l)}}\]

Termodinámicamente, esta reacción es espontánea en la dirección mostrada y tiene un cambio de energía libre estándar general (ΔG°) de -237 kJ por mol de agua producida.

Cuando esta reacción se produce electroquímicamente en la dirección espontánea (por ejemplo, en una pila de combustible de hidrógeno-aire), las dos reacciones de media celda que ocurren son:

Ánodo:\(\ce{H2_{(g)} ->2H^{+}_{(aq)} + 2e^{-}}\)

Cátodo:\(\ce{O2_{(g)} + 4H^{+}_{(aq)} + 4e^{-} -> 2H2O_{(l)}}\)

Aquí el ánodo es el electrodo negativo y el cátodo es el electrodo positivo; en condiciones de muy baja densidad de corriente (donde hay pérdidas resistivas mínimas y sobrepotenciales cinéticos), la diferencia de potencial que mediríamos entre los dos electrodos sería de 1.229 V.

En una celda electrolítica, esta reacción se realiza a la inversa. Es decir, ponemos energía eléctrica para dividir el agua en moléculas de hidrógeno y oxígeno. En este caso, las medias reacciones (y sus potenciales estándar) se revierten. O ₂ (g) se forman burbujas en el ánodo y H ₂ (g) se forma en el cátodo. Ahora el ánodo es el electrodo positivo y el cátodo es negativo. Los electrones se extraen de la sustancia en el ánodo (agua) y se bombean a la solución en el cátodo para producir hidrógeno. A continuación se muestra una animación de la media reacción del cátodo.

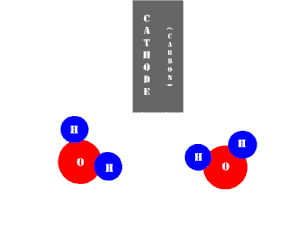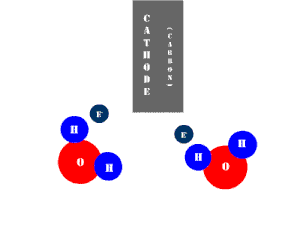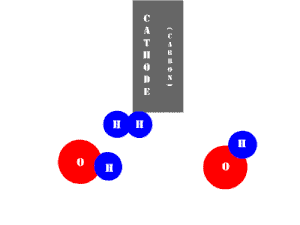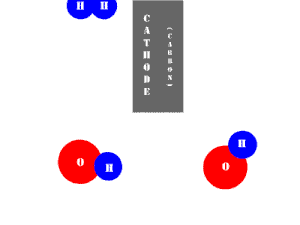
Tanto en celdas galvánicas como electrolíticas, la oxidación ocurre en el ánodo y la reducción ocurre en el cátodo.

Potenciales de media celda

Como se señaló anteriormente, el voltaje de equilibrio de una celda electroquímica es proporcional al cambio de energía libre de la reacción. Debido a que las reacciones electroquímicas pueden dividirse en dos medias reacciones, se deduce que los potenciales de las medias reacciones (como las energías libres) se pueden sumar y restar para dar un valor global para la reacción. Si tomamos como referencia el electrodo de hidrógeno estándar, es decir, si le asignamos un valor de cero voltios, podemos medir todas las otras medias celdas contra él y así obtener el voltaje de cada una. Esto nos permite clasificar las parejas redox de acuerdo a sus potenciales de reducción estándar (o más simplemente sus potenciales estándar), como se muestra en la siguiente tabla.

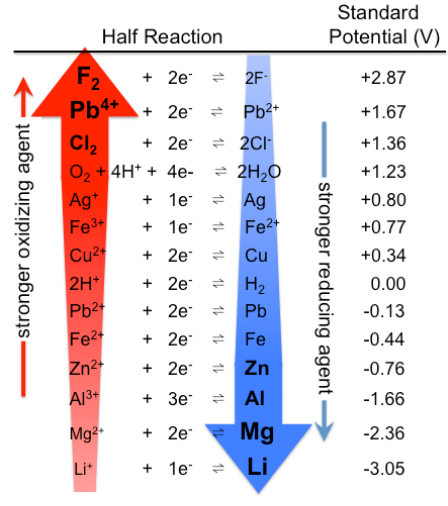
Tenga en cuenta que cuando construimos una celda electroquímica y calculamos el voltaje, simplemente tomamos la diferencia entre los potenciales de media celda y no nos preocupamos por el número de electrones en la reacción. Por ejemplo, para la reacción de desplazamiento en la que los iones de plata son reducidos por cobre metálico, la reacción es:

\(\ce{2Ag^{+}_{(aq)} + Cu_{(s)} = 2Ag_{(s)} + Cu^{2+}_{(aq)}}\)

Las dos reacciones semicelulares son:

\(Ag^{+}_{(aq)} + e^{-} =Ag_{(s)}\: \: + 0.80V\)

\(Cu^{2+}_{(aq)} + 2e^{-} = Cu_{(s)} \: \: + 0.34V\)

y el potencial estándar\(E^{o} = +0.80 - 0.34V = + 0.46V\)

La razón por la que no necesitamos multiplicar el potencial Ag por 2 es que E ^o es una medida del cambio de energía libre por electrón. Dividir el cambio de energía libre por el número de electrones (ver abajo) hace que E ^o sea una propiedad intensiva (como presión, temperatura, etc.).

Relación entre E y ΔG. Para sistemas que están en equilibrio,\( \Delta G^{o} = -nFE^{o}_{cell}\), donde n es número de moles de electrones por mol de productos y F es la constante de Faraday, ~96485 C/mol. Aquí el símbolo ^o indica que las sustancias involucradas en la reacción están en sus estados estándar. Por ejemplo, para la reacción de electrólisis del agua, los estados estándar serían agua líquida pura, H ⁺ a una concentración de 1M (o más precisamente, a actividad unitaria), y O ₂ y H ₂ (g) a una presión de 1 atmósfera.

Más generalmente (a cualquier concentración o presión),\(\Delta G = - nFE\), donde

\[E = E^{o} - \frac{RT}{nF} * lnQ\],

o a 298 K

\[E=E^{o} - \frac{0.0592}{n} * \log Q\]

donde Q es la relación de concentración de productos sobre reactivos, elevada a las potencias de sus coeficientes en la reacción. Esta ecuación (en cualquier forma) se llama la ecuación de Nernst. El segundo término en la ecuación, cuando se multiplica por -NF, es RT*lnQ. Esta es la diferencia de energía libre entre ΔG y ΔG°. Podemos pensar en esto como un término entrópico que toma en cuenta el cambio de entropía positivo de dilución, o el cambio de entropía negativo de concentrar un reactivo o producto, relativo a su estado estándar.

Usando la ecuación de Nernst

Ejemplo 1:

Para la media reacción\(\ce{2H^{+} + 2e^{-} = H_{2}}\), E° _1/2 = 0.000 V (por definición)

¿Qué es E _1/2 a pH 5 y P _{H 2} = 1 atm?
\(pH = -\log[H^{+}] = 5\), entonces [H ⁺] = 10 ^-5 M

\[E=E^{o} - \frac{0.0592}{2} * \log\frac{P_{H2}}{(H^{+})^{2}} = E^{o} - \frac{0.0592}{2} * \log(10^{5})^{2} = E^{o} - \frac{0.0592}{2}(10) = 0.000-0.296=-0.296V\]

Ejemplo 2:

¿Cuál es el potencial de una pila de combustible (una celda galvánica H _{2 /O 2}) operando a pH 5?

Reacción general:\(\ce{2H2_{(g)} + O2_{(g)} = 2H2O_{(l)}}\)

En esta reacción, H ₂ se oxida a H ⁺ y O ₂ se reduce a H ₂ O. Según nuestra convención, escribimos y equilibramos ambas reacciones de media célula como reducciones. Para mayor comodidad, hacemos esto en ácido. (Se deja como ejercicio al lector interesado para tratar de trabajar el problema en base)

Reacciones de media célula:

\(\ce{2H2_{(g)} = 4H^{+} + 4e^{-}}\)

\(\ce{O2_{(g)} + 4H^{+}_{(aq)} + 4e^{-} = 2H2O_{(l)}}\)

Autobús híbrido de pila de combustible Toyota. El bus funciona con energía eléctrica obtenida directamente de la reacción H 2 /O 2. Las celdas de combustible individuales se conectan en serie para hacer un tren de potencia que carga un paquete de baterías y acciona un motor eléctrico. Aunque el potencial estándar de la reacción es de 1.23 V, debido a los sobrepotenciales cinéticos cada celda de combustible en el tren de potencia opera a un voltaje de aproximadamente 0.70 V. A pesar de esta pérdida de energía, el sistema de celdas de combustible sigue siendo aproximadamente el doble de eficiente que un motor de combustión que realiza la misma reacción.

Para resolver este problema necesitamos encontrar la diferencia entre los potenciales de media celda H ₂/H ⁺ y O ₂ /H 2 O a pH 5.

\(\ce{2H^{+} + 2e^{-} -> H2}\)E° _1/2 = 0.000 V

Como todos los potenciales estándar, esto se escribe como una reducción. Necesitamos revertirlo y cambiar el signo de E ^o ya que H ₂ está siendo oxidado:

\(\ce{H2 -> 2H^{+} + 2e^{-}}\)E° _1/2 = -0.000 V

y añadir el potencial estándar de la sustancia que se está reduciendo en el cátodo:

\(\ce{O2 + 4H^{+} + 4e^{-} -> 2H2O}\)E° _1/2 = +1.229 V

La diferencia entre los dos potenciales estándar de media celda es +1.229 - 0.000 = +1.229 V

_Celda E° = +1.229 Voltios

Ahora usamos la ecuación de Nernst para dar cuenta del hecho de que H ⁺ no está en su estado estándar:

\[ E_{cell} = E^{o} -\frac{0.0592}{4} * log \frac{[H^{+}]^{4}}{P_{O2}P^{2}_{H2}[H^{+}]^{4}} = E^{o} -\frac{0.0592}{4}* log(1) = E^{o} = + 1.229V\]

Obsérvese que el valor de la _celda E no cambia con el pH ya que ambas parejas desplazan -59.2 mV/pH de acuerdo con la ecuación de Nernst. Esta es la consecuencia de que el número de electrones es igual al número de protones en cada una de las reacciones de media célula. Otra forma de racionalizar este resultado es recordar que la reacción global (2H ₂ + O ₂ = 2H ₂ O) no involucra a H ⁺ como reactivo o producto, por lo que ΔG y E deben ser independientes del pH.

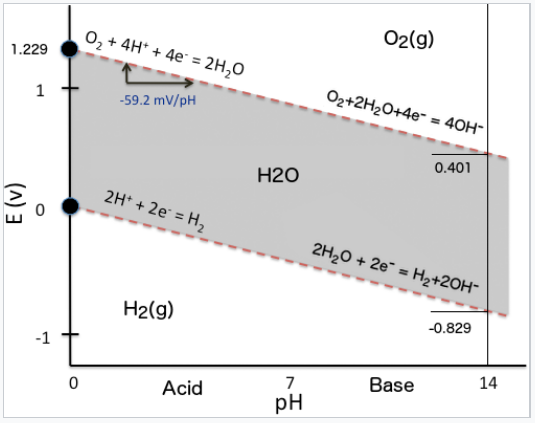
_{Podemos graficar el cambio en los potenciales de media celda H 2/H ⁺ y O 2/H 2 O con pH en un diagrama de potencial-pH (también llamado diagrama de Pourbaix) como se muestra a continuación.} Los potenciales dependientes del pH de las parejas H ₂ y O ₂ se muestran como líneas punteadas. Observe que la diferencia de potencial entre ellos es siempre de 1.23 V. Las ojeras representan los potenciales estándar.

Diagrama Pourbaix para agua.

Los diagramas de Pourbaix son esencialmente diagramas de fase electroquímicos, que representan regiones de estabilidad termodinámica para sustancias redox activas. Al igual que en otros tipos de diagramas de fases, las líneas representan condiciones bajo las cuales dos fases coexisten en equilibrio. El área sombreada en el diagrama de agua Pourbaix representa las condiciones de potencial y pH donde el agua líquida es estable en relación con hidrógeno u oxígeno. Fuera de la región sombreada, el agua es termodinámicamente inestable y se reduce a H ₂ (g) u oxidada a O ₂ (g). Aunque estos procesos son espontáneos en el sentido termodinámico (por ejemplo, el agua es inestable en presencia de Pb ⁴⁺, Cl ₂, Fe, Zn o Al), son cinéticamente lentos y requieren catálisis para proceder.