6.8: Ferro-, Ferri- y Antiferromagnetismo
- Page ID
- 71914
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
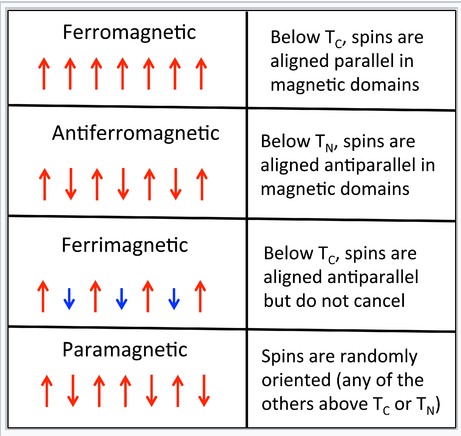
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El magnetismo de los metales y otros materiales está determinado por los movimientos orbitales y de espín de los electrones desapareados y la forma en que los electrones desapareados se alinean entre sí. Todas las sustancias magnéticas son paramagnéticas a temperatura suficientemente alta, donde la energía térmica (kT) excede la energía de interacción entre espines en átomos vecinos. Por debajo de cierta temperatura crítica, los giros pueden adoptar diferentes tipos de arreglos ordenados.
|
Una descripción pictórica del orden de los espines en ferromagnetismo, antiferromagnetismo, ferrimagnetismo y paramagnetismo |
Comencemos considerando un átomo individual en la estructura bcc del metal de hierro. El Fe está en el grupo VIIIb de la tabla periódica, por lo que tiene ocho electrones de valencia. El átomo es promovido al estado 4s 1 3d 7 con el fin de hacer enlaces. Una imagen localizada de los electrones d para un átomo de hierro individual podría verse así:

Dado que cada electrón desapareado tiene un momento de espín de 1/2, el momento angular de giro total, S, para este átomo es:
\(S = 3\frac{1}{2} = \frac{3}{2}\)(en unidades de h/2π)
Podemos pensar en cada átomo de Fe en el sólido como un pequeño imán de barra con un momento de solo giro S de 3/2. Los momentos de espín de átomos neigaburridos pueden alinearse en forma paralela (↑ ↑), antiparalela (↑ ↓) o aleatoria. En bcc Fe, la tendencia es alinearse en paralelo debido al signo positivo de la interacción de intercambio. Esto da como resultado un ordenamiento ferromagnético, en el que todos los espines dentro de un dominio magnético (típicamente cientos de celdas unitarias de ancho) tienen la misma orientación, como se muestra en la figura de la derecha. Por el contrario, una interacción de intercambio negativo entre los átomos vecinos en Cr bcc resulta en un ordenamiento antiferromagnético. Un tercer arreglo, el orden ferrimagnético, resulta de una alineación antiparalela de espines en átomos vecinos cuando los momentos magnéticos de los vecinos son desiguales. En este caso, los momentos de giro no se cancelan y hay una magnetización neta. El mecanismo de ordenación es como el de un sólido antiferromagnético, pero las propiedades magnéticas se asemejan a las de un ferroimán. El ordenamiento ferrimagnético es más común en los óxidos metálicos, como aprenderemos en el Capítulo 7.
Magnetización y susceptibilidad
La susceptibilidad magnética, χ, de un sólido depende del orden de los giros. Los sólidos paramagnéticos, ferromagnéticos, antiferromagnéticos y ferrimagnéticos tienen χ > 0, pero la magnitud de su susceptibilidad varía con el tipo de orden y con la temperatura. Veremos este tipo de ordenamiento magnético principalmente entre los elementos 3d y 4f y sus aleaciones y compuestos. Por ejemplo, Fe, Co, Ni, Nd 2 Fe 14 B, SmCo 5 e YCo 5 son todos ferroimanes, Cr y MnO son antiferroimanes, y Fe 3 O 4 y CoFe 2 O 4 son ferriimanes. Los compuestos diamagnéticos tienen una susceptibilidad negativa débil (χ < 0).
Definiciones
- H = campo magnético aplicado (unidades: Henry (H))
- B = campo magnético inducido en un material (unidades: Tesla (T))
- M = magnetización, que representa los momentos magnéticos dentro de un material en presencia de un campo externo H.
Susceptibilidad magnética χ = M/H
Por lo general, χ se da en unidades molares en el sistema cgs:
χ M = susceptibilidad molar (unidades: cm 3 /mol)
Valores típicos de χ M:
| Compuesto | Tipo de Magnetismo | χ a 300K (cm 3 /mol) |
|---|---|---|
| SiO 2 | Diamagnético | - 3 x 10 -4 |
| Pt metal | Pauli paramagnético | + 2 x 10 -4 |
| Gd 2 (SO 4) 3. 8H 2 O | Paramagnético | + 5 x 10 -2 |
| Aleación de Ni-Fe | Ferromagnético | + 10 4 - 10 6 |
Para correlacionar χ con el número de electrones desapareados en un compuesto, primero corrigimos la pequeña contribución diamagnética de los electrones centrales:
\[\chi^{corr} = \chi^{obs}- \chi^{diamagnetic\: cores}\]
Susceptibilidad de paramagnets
Para una sustancia paramagnética,
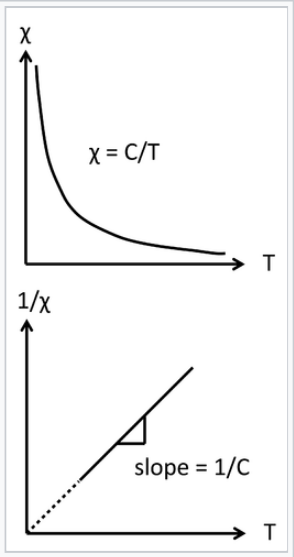
\[\chi^{corr}_{M} = \frac{C}{T}\]
La relación inversa entre la susceptibilidad magnética y T, la temperatura absoluta, se llama Ley de Curie, y la constante de proporcionalidad C es la constante de Curie:
\[C= \frac{N_{A}}{3k_{B}}\mu^{2}_{eff}\]
Obsérvese que C no es una “constante” en el sentido habitual, porque depende de µ eff, el momento magnético efectivo de la molécula o ion, que a su vez depende de su número de electrones desapareados:
\[\mu_{eff} = \sqrt{n(n+2)}\mu_{B}\]
|
Comportamiento de la ley Curie de un paramagnet. Una gráfica de 1/χ vs. temperatura absoluta es una línea recta, con una pendiente de 1/C y una intercepción de cero. |
Aquí µ B es el magnetón Bohr, una constante física definida como µ B = eh/4πm e = 9.274 x 10-21 erg/gauss (en unidades cgs).
En unidades cgs, podemos combinar constantes físicas,
\[\frac{N_{A}}{3k_{B}} \mu^{2}_{B} = .125\]
Combinando estas ecuaciones, obtenemos
\[\chi^{corr}_{M} = \frac{.125}{T}(\frac{\mu_{eff}}{\mu_{B}})^{2}\]
Estas ecuaciones relacionan la susceptibilidad molar, una cantidad aparente que se puede medir con un magnetómetro, con µ eff, una cantidad que se puede calcular a partir del número de electrones desapareados, n. Dos puntos importantes a tener en cuenta sobre esta fórmula son:
- La susceptibilidad magnética es inversamente proporcional a la temperatura absoluta, con una constante de proporcionalidad C (Ley de Curie)
- Hasta el momento estamos hablando sólo de sustancias paramagnéticas, donde no hay interacción entre los átomos vecinos.
|
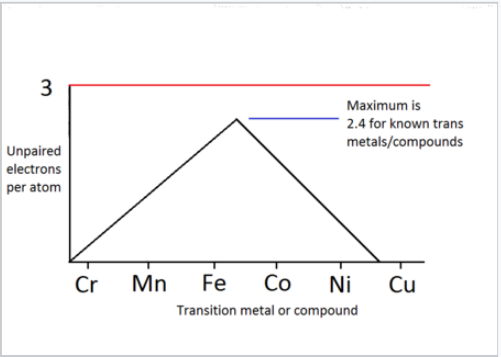
Número de electrones desapareados por átomo, determinado a partir de las constantes Curie de los metales de transición y sus aleaciones 1:1. |
Volviendo al átomo de Fe aislado con sus tres electrones desapareados, podemos medir la constante de Curie para hierro metálico (por encima de la temperatura de su transición a un sólido paramagnético) y compararla con el cálculo de µ eff. Desde n = 3, calculamos:
\[\mu_{eff}= \sqrt{(3)(5)} \mu_{B} = 3.87\mu_{B}\]
La gráfica de la derecha muestra el número de electrones desapareados por átomo, calculado a partir de las constantes de Curie medidas, para los elementos magnéticos y aleaciones 1:1 en la serie 3d. La gráfica alcanza un pico a un valor de 2.4 espines por átomo, ligeramente inferior a lo que calculamos para un átomo de hierro aislado. Esto refleja ese hecho de que existe algún emparejamiento de electrones d, es decir, que sí contribuyen un poco a la unión en esta parte de la tabla periódica.
Susceptibilidad de ferro, ferri y antiferroimanes
Por debajo de cierta temperatura crítica, los espines de un orden de sustancia paramagnética sólida y la susceptibilidad se desvían del comportamiento simple de la ley de Curie. Debido a que el orden depende de la interacción de intercambio de corto alcance, esta temperatura crítica varía ampliamente. Los metales y aleaciones en la serie 3d tienden a tener altas temperaturas críticas porque los átomos están unidos directamente entre sí y la interacción es fuerte. Por ejemplo, Fe y Co tienen temperaturas críticas (también llamadas temperatura de Curie, T c, para sustancias ferromagnéticas) de 1043 y 1400 K, respectivamente. La temperatura de Curie está determinada por la fuerza de la interacción de intercambio magnético y por el número de electrones desapareados por átomo. El número de electrones desapareados alcanza los picos entre Fe y Co a medida que se llena la banda d, y la interacción de intercambio es más fuerte para Co que para Fe. A diferencia de los metales y aleaciones ferromagnéticos, las sales paramagnéticas de iones de metales de transición típicamente tienen temperaturas críticas por debajo de 1K porque los iones magnéticos no están directamente unidos entre sí y por lo tanto sus espines están muy débilmente acoplados en estado sólido. Por ejemplo, en el sulfato de gadolinio, los iones paramagnéticos Gd 3 + se aíslan entre sí por iones SO 4 2 -.
|
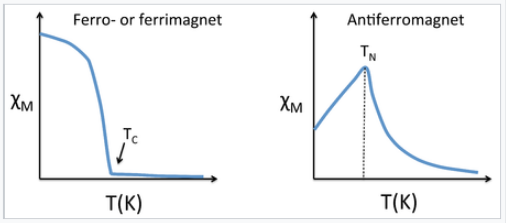
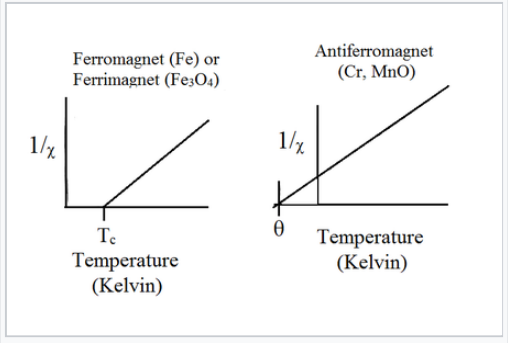
Susceptibilidad magnética vs temperatura (Kelvin) para materiales ferrimagnéticos, ferromagnéticos y antiferromagnéticos |
Por encima de la temperatura crítica T C, los compuestos ferromagnéticos se vuelven paramagnéticos y obedecen a la ley Curie-Weiss:
\[\chi= \frac{C}{T-T_{c}}\]
Esto es similar a la ley de Curie, excepto que la gráfica de 1/χ vs. T se desplaza a una intercepción positiva T C en el eje de temperatura. Esto refleja el hecho de que los materiales ferromagnéticos (en su estado paramagnético) tienen una mayor tendencia a que sus espines se alineen en un campo magnético que un paramagnet ordinario en el que los espines no interactúan entre sí. Los ferriimanes siguen el mismo tipo de comportamiento de orden. Las gráficas típicas de χ vs. T y 1/χ vs. T para ferro-/ferriimanes se muestran arriba y abajo.
|
Gráficas de 1/χ vs. T para ferroimanes, ferriimanes y antiferroimanes. |
Los sólidos antiferromagnéticos también son paramagnéticos por encima de una temperatura crítica, que se llama la temperatura de Néel, T N. Para los antiferroimanes, χ alcanza un máximo en T N y es menor a mayor temperatura (donde los giros paramagnéticos están más desordenados por la energía térmica) y a menor temperatura (donde los espines se emparejan). Por lo general, los antiferroimanes conservan cierta susceptibilidad positiva incluso a temperaturas muy bajas debido a la inclinación de sus espines emparejados. Sin embargo, el valor máximo de χ es mucho menor para un antiferroimán que para un ferro- o ferriimán. La ley Curie-Weiss también se modifica para un antiferroimán, reflejando la tendencia de los espines (en el estado paramagnético por encima de T N) a resistir el ordenamiento paralelo. Una gráfica de 1/χ vs. T intercepta el eje de temperatura a una temperatura negativa, -θ, y la ley de Curie-Weiss se convierte en:
\[\chi= \frac{C}{T + \theta}\]
Ordenación de giros por debajo de T C
Por debajo de T C, los espines se alinean espontáneamente en ferro y ferriimanes. Se observa un comportamiento complejo de magnetización que depende de la historia de la muestra. Por ejemplo, si un material ferromagnético se enfría en ausencia de un campo magnético aplicado, forma una estructura en mosaico de dominios magnéticos que cada uno tiene espines alineados internamente. Sin embargo, los dominios vecinos tienden a alinearse de manera opuesta para minimizar la energía total del sistema. Esto se ilustra en la figura de la izquierda para un imán Nd-Fe-B. La muestra consiste en granos de cristal de 5-10 µm de ancho que se pueden distinguir fácilmente por los límites nítidos en la imagen. Dentro de cada grano hay una serie de franjas más claras y oscuras (obtenidas mediante el efecto Kerr óptico) que son dominios ferromagnéticos con orientaciones opuestas. Promedios sobre toda la muestra, estos dominios tienen orientación aleatoria por lo que la magnetización neta es cero.
|
Granos microcristalinos dentro de una pieza de Nd 2 Fe 14 B (la aleación utilizada en los imanes de neodimio) con dominios magnéticos visibles con un microscopio Kerr. Los dominios son las franjas claras y oscuras visibles dentro de cada grano. |
Cuando una muestra como esta es magnetizada (es decir, expuesta a un campo magnético fuerte), las paredes de dominio se mueven y los dominios favorablemente alineados crecen a expensas de aquellos con la orientación opuesta. Esta transformación se puede ver en tiempo real en el microscopio Kerr. Las paredes de dominio suelen tener cientos de átomos de ancho, por lo que el movimiento de una pared de dominio implica una inclinación cooperativa de orientación de giro (análoga a “la ola” en un estadio deportivo) y es un proceso de energía relativamente baja.
|
El movimiento de las paredes de dominio en un grano de acero al silicio es impulsado en esta película al aumentar el campo magnético externo en la dirección “hacia abajo”, y se obtiene una imagen usando un microscopio Kerr. Las áreas blancas son dominios con su magnetización dirigida hacia arriba, las áreas oscuras -que eventualmente comprenden todo el grano- son dominios con su magnetización dirigida hacia abajo. |
El proceso de magnetización aleja al sólido de su estado de energía más bajo (orientación de dominio aleatorio), por lo que la magnetización implica la entrada de energía. Cuando se elimina el campo magnético externo, las paredes del dominio se relajan un poco, pero el sólido (especialmente en el caso de un imán “duro”) puede retener gran parte de su magnetización. Si alguna vez has magnetizado un clavo o un clip usando un imán permanente, lo que estabas haciendo era mover las paredes de los dominios magnéticos dentro del ferroimán. El objeto a partir de entonces conserva la “memoria” de su magnetización. Sin embargo, el recocido de un imán permanente destruye la magnetización al devolver el sistema a su estado de energía más baja en el que todos los dominios magnéticos se cancelan entre sí.
|
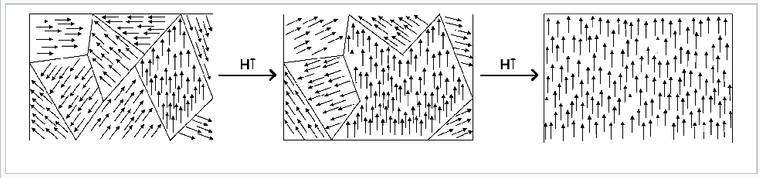
Rotación de orientación y aumento de tamaño de dominios magnéticos en respuesta a un campo magnético aplicado externamente. |
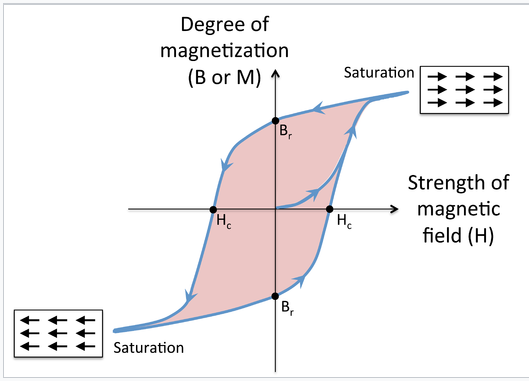
Histéresis magnética. El ciclado de un material ferro o ferrimagnético en un campo magnético da como resultado histéresis en la magnetización del material, como se muestra en la figura de la izquierda. Al principio, la magnetización es cero, pero comienza a subir rápidamente a medida que se aplica el campo magnético. En campo alto, los dominios magnéticos están alineados y se dice que la magnetización está saturada. Cuando se elimina el campo, se retiene una cierta magnetización remanente (indicada como el punto B r en la gráfica), es decir, se magnetiza el material. Aplicando un campo en la dirección opuesta comienza a orientar los dominios magnéticos en la otra dirección, y en un campo Hc (el campo coercitivo), la magnetización de la muestra se reduce a cero. Eventualmente el material alcanza la saturación en dirección opuesta, y cuando el campo se retira nuevamente, tiene magnetización remanente Br, pero en sentido contrario. A medida que el campo continúa revertiéndose, el imán sigue el bucle de histéresis como lo indican las flechas. El área de la región coloreada dentro del bucle es proporcional al trabajo magnético realizado en cada ciclo. Cuando el campo circula rápidamente (por ejemplo, en el núcleo de un transformador, o en ciclos de lectura-escritura de un disco magnético) este trabajo se convierte en calor.
|
Magnetización de un ferro- o ferriimán vs. campo magnético aplicado H. Comenzando en el origen, la curva ascendente es la curva de magnetización inicial. La curva descendente después de la saturación, junto con la curva de retorno inferior, forman el bucle principal. Las intercepciones Hc y Br son la coercitividad y la magnetización remanente. |