9.3: Energética de Sólidos Cristalinos- El Modelo Iónico

Muchos compuestos iónicos tienen estructuras simples. Debido a que las fuerzas que mantienen unidos los átomos son principalmente electrostáticas, podemos calcular la energía cohesiva de la red cristalina con buena precisión. Preguntas interesantes para hacer sobre estos cálculos de energía de celosía son:

• ¿Qué tan precisos son los cálculos de energía reticular?
• ¿Qué nos enseñan sobre los enlaces químicos en los cristales iónicos?
• ¿Podemos usar energías de celosía para predecir propiedades como solubilidad, estabilidad y reactividad?
• ¿Podemos usar energías de celosía para predecir las estructuras cristalinas de los compuestos iónicos?

Empecemos por mirar las fuerzas que mantienen unidas las celosías iónicas. Existen principalmente dos tipos de fuerza que determinan la energía de un enlace iónico.

La estructura cristalina de NaCl es el arquetipo para calcular las energías de la red y calcular entalpías de formación a partir de ciclos de Born-Haber.

1) Fuerza electrostática de atracción y repulsión (Ley de Coulomb): Dos iones con cargas z ₊ y z _-, separados por una distancia r, experimentan una fuerza F:

\[\mathbf{F} = -\frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r^{2}}\]

donde

e = 1.6022×10 ⁻¹⁹ C

4 π ε ₀ = 1.112×10 ⁻¹⁰ C²/ (J m)

Esta fuerza es atractiva para iones de carga opuesta.

La energía potencial electrostática, E _elec, es dada entonces por

\[\mathbf{E}_{elec} \int_{\infty}^{r} F(r)dr = \frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r}\]

El signo de E _elec es negativo para la interacción atractiva entre un catión y un anión. Es decir, cuanto más cerca se acercan los iones con carga opuesta, menor es la energía potencial.

2) Repulsión de caparazón cerrado. Cuando los electrones en las conchas cerradas de un ion se superponen con los de otro ion, hay una fuerza repulsiva que proviene del principio de exclusión Pauli. Un tercer electrón no puede entrar en un orbital que ya contiene dos electrones. Esta fuerza es de corto alcance, y típicamente se modela como cayendo exponencialmente o con una alta potencia de la distancia r entre átomos. Por ejemplo, en la aproximación Born, B es una constante y ρ es un número con unidades de longitud, que generalmente se determina empíricamente a partir de datos de compresibilidad. Un valor típico de ρ es 0.345 Å.

\[\mathbf{E}_{repulsion} = Bexp(\frac{-r}{\rho})\]

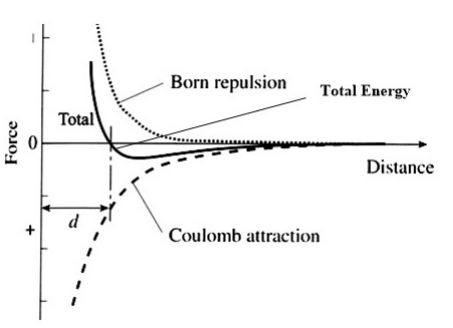
La energía del enlace iónico entre dos átomos se calcula entonces como la combinación de energías electrostáticas netas y de repulsión de concha cerrada, como se muestra en la figura de la derecha. Tenga en cuenta que por el momento estamos ignorando la atractiva energía de van der Waals entre iones, que explicaremos a continuación. Para un par de iones, la distancia de equilibrio entre iones está determinada por el mínimo en la curva de energía total. A esta distancia, la fuerza neta sobre cada ion es cero.

Energía electrostática de una red cristalina

Podemos usar estas ecuaciones para calcular la energía reticular de un cristal sumando las interacciones entre todos los pares de iones. Debido a que la fuerza de repulsión de capa cerrada es de corto alcance, este término generalmente se calcula solo para interacciones entre iones vecinos. Sin embargo, la fuerza de Coulomb es de largo alcance, y debe calcularse sobre todo el cristal. Este problema fue resuelto por primera vez en 1918 por Erwin Madelung, un físico alemán. ^[4]

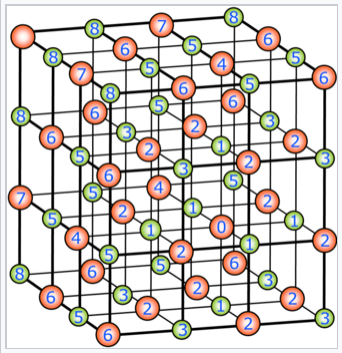
Considere un ion en la estructura de NaCl etiquetado como “O” en el diagrama de la derecha. Podemos ver que las interacciones vecinas más cercanas (+ -) con iones etiquetados “1" son atractivas, las siguientes interacciones vecinas más cercanas (- - y + +) son repulsivas, y así sucesivamente. En la estructura de NaCl, contando desde el ion en el centro de la celda unitaria, hay 6 vecinos más cercanos (en las caras del cubo), 12 vecinos siguientes más cercanos (en los bordes del cubo), 8 en la siguiente concha (en los vértices del cubo), y así sucesivamente. Sus distancias desde el ion “0" aumentan progresivamente: r _o, √2 r _o, √3 r _o, y así sucesivamente, donde r _o es la distancia vecina más cercana.

Ahora podemos escribir la energía electrostática en el ion “O” como:

\[\mathbf{E}_{elec} = -6\frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}} + 12 \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{\sqrt{2}r_{o}} -8 \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{\sqrt{3}r_{o}} + \dots \]

Factorizando las constantes y la distancia de enlace vecino más cercano r _o obtenemos:

\[\mathbf{E}_{elec} = \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}}(6 - \frac{12}{\sqrt{2}} + \frac{8}{\sqrt{3}} - \frac{6}{\sqrt{4}} + \dots) \]

Donde la suma entre paréntesis, que es sin unidades, converge lentamente a un valor de A = 1.74756. Generalizando esta fórmula para cualquier cristal iónico tridimensional obtenemos una función:

\[\mathbf{E}_{elec} = \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}} NA\]

donde N es el número de Avogadro (porque estamos calculando energía por mol de iones) y A se llama la constante Madelung. La constante de Madelung depende únicamente de la disposición geométrica de los iones y por lo tanto varía entre diferentes tipos de estructuras cristalinas, pero dentro de un tipo de estructura dado no cambia. Por lo tanto, MgO y NaCl tienen la misma constante de Madelung porque ambos tienen la estructura de NaCl

La constante de Madelung se calcula sumando las interacciones electrostáticas con el ion marcado 0 en el método de las esferas de expansión. Cada número designa el orden en que se suma. Por ejemplo, los iones marcados con 1 representan los seis vecinos más cercanos (interacción atractiva), los iones marcados con 2 son los 12 siguientes vecinos más cercanos (interacción repulsiva) y así sucesivamente. Tenga en cuenta que si la suma se lleva a cabo sobre conchas 1-2-3..., converge muy lentamente, pero existen métodos matemáticos para sumarla que dan una serie rápidamente convergente.

La siguiente tabla enumera las constantes de Madelung para algunas estructuras comunes. La constante reducida de Madelung se obtiene normalizando los valores al número de iones en la unidad de fórmula. Se puede ver en la tabla que las constantes reducidas de Madelung son bastante similares para diferentes estructuras. Esto hace que sea difícil determinar sobre la base de cálculos de energía electrostática qué estructura será más estable para un compuesto dado. Es interesante observar que la tendencia en las constantes reducidas de Madelung sigue aproximadamente la tendencia en ionicidad (cf. el diagrama de Mooser-Pearson en la Sección 9.2). Por ejemplo, la wurtzita tiene una constante de Madelung ligeramente mayor que el zincblende, consistente con nuestra conclusión anterior de que la estructura de wurtzita es favorecida por compuestos más polares.

Estructura	Constante de Madelung, A	Constante de Madelung Reducida, 2a/N
NaCl (halita)	1.7476	1.7476
CsCl	1.7627	1.7627
ZnS (zincblende)	1.6381	1.6381
ZnS (wurtzita)	1.6413	1.6413
CaF 2 (fluorita)	2.5194	1.6796
TiO 2 (rutilo)	2.4080	1.6053
Al 2 O 3 (corindón)	4.172	1.6688

Energía total de celosía de un cristal

Teniendo en la mano una fórmula para la energía electrostática, ahora podemos agregar en el término de repulsión de caparazón cerrado para obtener una ecuación que nos dé la energía total de la red.

\[E_{L} = \frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}} NA + NBexp(\frac{-r}{\rho})\]

A la distancia del enlace de equilibrio, las fuerzas sobre todos los iones son cero, y podemos usar este hecho para eliminar la constante B:

\[[\frac{dE}{dr}]_{r=r_{o}} = 0\]

Expresado de esta manera, E _L es un número negativo (porque z ₊ y z _- tienen signos opuestos). Representa el cambio de energía para formar un mol de sal sólida a partir de un mol de los iones gaseosos, separados inicialmente a una distancia infinita.

El fluoruro de litio (mostrado aquí como un monocristal grande en un vaso de precipitados de agua) es el único haluro alcalino que no es libremente soluble en agua. La energía reticular de LiF es la más negativa de los fluoruros alcalinos porque Li ^+ y F ^- son ambos iones pequeños y E L es proporcional a 1/r 0.