9.4: Ciclos de Nacido-Haber para NaCl y Halouros de Plata

Última actualización
Guardar como PDF

Page ID: 72225

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ahora que tenemos una ecuación para la energía reticular de un cristal iónico, podemos preguntarnos qué tan precisa es. Recuerden, hicimos varias aproximaciones para llegar a esta fórmula. Supusimos que la red era completamente iónica, ignoramos la energía atractiva de van der Waals de los iones, y asumimos que no hubo contribución covalente a la unión.

Consideremos la energía reticular de la sal de mesa (NaCl)

\(\ce{Na^{+}_{(g)} + Cl^{-}_{(g)} -> NaCl_{(s)}}\)

Para calcular la energía de celosía, agrupamos las constantes físicas:

\[E_{L} (\frac{kJ}{mol}) = (1389.3) \frac{Aq_{1}q_{2}}{r_{o}}(1-\frac{.345}{r_{o}})\]

donde r _o se expresa en Å. Ahora podemos calcular la energía reticular para NaCl usando r _o = 2.814 Å, como:

\[E_{L} = -(1389.3) \frac{1.7476}{2.814} (1 -\frac{.345}{2.814}) = -766.5 \frac{kJ}{mol}\]

Alternativamente, podemos construir un ciclo Born-Haber para la formación de NaCl a partir de los elementos y calcular la energía reticular como el término “faltante” en el ciclo.

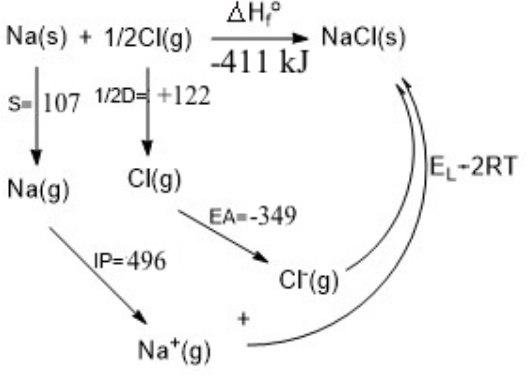
Ciclo de Born Harber

S= Energía de sublimación de Na (s)

IP= Potencial de ionización de Na (g)

D= Energía de disección de enlace de Cl ₂ (g)

EA= Afinidad electrónica de Cl (g)

E _L =Energía de celosía de NaCl

R= Constante de gas

T= Temperatura absoluta

De la Ley de Hess':\(\Delta H_{f} = s + \frac{1}{2}D + IP + EA + E_{L} -2RT = \mathbf{-396 \frac{kJ}{mol}}\)

Aquí tenemos que restar 2RT para convertir nuestro ciclo de energías en un ciclo de entalpías, porque estamos comprimiendo dos moles de gas en la elaboración de NaCl (s) y PΔV = ΔnRT, donde Δn = -2.

Experimentalmente ΔH _f para NaCl es -411 kJ/mol

Debido a que todos los demás números del ciclo se conocen con precisión, el error en nuestro cálculo es de sólo unos 15 kJ (aproximadamente 2% de E _L). El resultado es prometedor porque descuidamos el término de van der Waals.

Pero... ¿cómo nos salimos con la suya descuidando el término de van der Waals?

Esto se debe a que utilizamos la minimización de energía para obtener la energía de repulsión en la ecuación de Born-Mayer. Si subestimamos la energía atractiva de la red cristalina, el criterio de minimización de energía asegura que también se subestime la energía de repulsión. Los dos errores compensan parcialmente, por lo que el error general en el cálculo es pequeño.

Podemos hacerlo mejor incluyendo explícitamente la energía atractiva de van der Waals de corto alcance entre iones. La siguiente tabla muestra los resultados de cálculos de energía reticular más detallados para fluoruros iónicos en los que se incluye explícitamente el término van der Waals. Los errores en este caso son sólo alrededor del 1% de E _L.

Compuesto	Energía de celosía calculada (kJ/mol)	Experimental E _L del Ciclo Nacido-Haber
MGF ₂ (estructura de rutilo)	-2,920	-2,908
CaF ₂ (estructura de fluorita)	-2,586	-2,611
BaF ₂ (estructura de fluorita)	-2,326	-2,368

Halouros de Plata

Es interesante repetir este ejercicio para los haluros de plata, que tienen la estructura de NaCl (AgF, AgCl, AgBr) o la estructura de zincblende (AGi).

Halouros de Plata	Calculado	Ciclo	Diferencia (kJ/mol)
AgF	-920	-954	34
AgCl	-833	-908	75
AgBr	-816	-900	84
AGi	-778	-883	105

Al mirar la tabla, vemos que el error es pequeño para aGF y se hace progresivamente más grande para los haluros de plata más pesados. Sin embargo todavía estamos obteniendo respuestas dentro de aproximadamente 12% de error incluso para AGi. ¿Debemos interpretar la buena concordancia con los valores calculados a partir del modelo iónico para significar que estos compuestos son iónicos? Claramente, esta descripción es inapropiada para AGi, donde la diferencia de electronegatividad Δχ es solo 0.6 (compare este valor con 0.4 para un enlace C-H, que normalmente vemos como no polar).

Una gota de solución de nitrato siver, cuando se agrega a una solución diluida de ácido clorhídrico, da como resultado la formación inmediata de un precipitado de cloruro de plata blanco. Esta reacción se utiliza como prueba cualitativa para la presencia de iones haluro en soluciones. La contribución de enlace covalente a las energías reticulares de AgCl, AgBr y AgI hace que estas sales sean escasamente solubles en agua.

Nuevamente, podemos interpretar el acuerdo fortuito entre las energías calculadas y obtenidas experimentalmente en términos de errores compensadores. Nuestro cálculo de energía reticular sobreestima la contribución iónica en el caso de los haluros de plata más pesados, pero subestima la contribución covalente. De estos compuestos, solo el AgF es soluble en agua y debe pensarse como un compuesto iónico. Los otros son progresivamente más insolubles en agua (K _sp es ^{10-10, ^10-13} y ^10-16 para AgCl, AgBr y AgI), reflejando una creciente covalencia a medida que Δχ disminuye.

La moraleja de la historia es que los simples cálculos de energía de celosía basados en el modelo iónico funcionan bien, ¡pero no necesariamente implican que los compuestos sean iónicos!