Saltar al contenido principal
LibreTexts Español

1.14: Método de superposición angular y diatómica M-L

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    74678

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La aproximación de Wolfsberg-Hemholtz (Lecture 10) proporcionó la energía LCAO-MO entre el metal y el ligando para ser,

    $$
    \ varepsilon_ {\ sigma} =\ frac {\ mathrm {E} _ {\ mathrm {M}} ^ {2}\ mathrm {~S} _ {\ mathrm {ML}} ^ {2}} {\ Delta\ mathrm {E} _ {\ mathrm {ML}}}\ quad\ varepsilon_ {\ sigma^ {*} =\ frac {\ mathrm {E} _ {\ mathrm {L}} ^ {2}\ mathrm {~S} _ {\ mathrm {ML}} ^ {2}} {\ Delta\ mathrm {E} _ _ {\ mathrm {ML}}}
    \]

    Tenga en cuenta que E M, E L y ΔE ML en las expresiones anteriores son constantes. Por lo tanto, el MO dentro del marco Wolfsberg-Hemholtz escala directamente con la integral de superposición, S ML

    $$
    \ varepsilon_ {\ sigma} =\ frac {\ mathrm {E} _ {\ mathrm {M}} {} ^ {2}\ mathrm {~S} _ {\ mathrm {ML}} ^ {2}} {\ Delta\ mathrm {E} _ _ {\ mathrm {ML}}} =\ beta^ {\ prime}\ mathrm {S} {\ mathrm {ML}} ^ {2}\ quad\ varepsilon_ {\ sigma^ {*}} =\ frac {\ mathrm {E} _ {\ mathrm {L}} ^ {2}\ mathrm {~S} _ {\ mathrm {ML}} ^ {2}} {\ Delta\ mathrm {E} _ {\ mathrm {ML}} =\ beta\ mathrm {S} _ {\ mathrm {ML}} {} ^ {2}
    \]

    donde las constantes β y β'es. Por lo tanto, determinando la integral de solapamiento, S ML, las energías de los MO pueden determinarse en relación con los orbitales atómicos de metal y ligando.

    El Método de Superposición Angular (AOM), proporciona una medida de los niveles de energía S ML y, por lo tanto, MO. En AOM, la integral de superposición también se factoriza en un producto radial y angular,

    S ML =S (r) F (θ, Φ)

    Analizando S (r) en función de la distancia internuclear M—L,

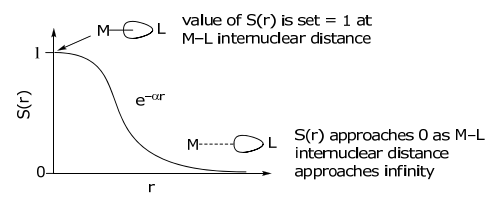
    clipboard_e4b60b5d078fbbe83feb6e1fb5263367a.png

    Bajo la condición de una distancia M-L fija, S (r) es invariante, y por lo tanto la integral de superposición, S ML, dependerá únicamente de la dependencia angular, es decir, de F (θ, φ).

    Debido a que el orbital σ es simétrico, la dependencia angular, F (θ, φ), de la integral de superposición refleja la dependencia angular del orbital central.

    p-orbital

    ... se define angularmente por una función cos θ. De ahí que la dependencia angular de un orbital σ a medida que gira angularmente alrededor de un orbital p refleja la dependencia angular cos θ del orbital p.

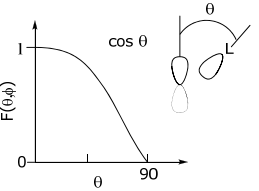
    clipboard_e0005e637201ff7b4a1b7457111c9d153.png

    De igual manera, los otros orbitales asumen la dependencia angular de la órbita metálica central. Por lo tanto, para

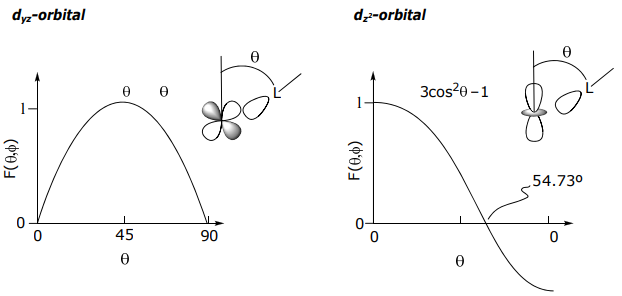
    clipboard_e153215dcd85cf610067fbacdbb27ca25.png

    Complejos diatómicos ML

    Para comenzar, determinemos la energía de los orbitales d para un diatómico M-L definido por el siguiente sistema de coordenadas,

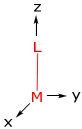
    clipboard_ecfe7d8647869eb3f3f6a3cd13674e4ff.png

    Existen tres tipos de interacciones de solapamiento basadas en simetrías orbitales de ligandos σ, π y δ. Para un orbital σ, la interacción se define como,

    clipboard_ebaec567bb17ec8f996ed75474cc5aae2.png

    $$
    \ mathrm {E}\ left (\ mathrm {d} _ _ {z^ {2}}\ derecha) =\ mathrm {S} _ {\ mathrm {ML}} ^ {2} (\ sigma) =\ beta\ cdot\ mathrm {F} _ {\ sigma} {} ^ {2} (\ theta,\ phi) =\ beta\ cdot 1=\ mathrm {e}\ sigma
    \]

    La energía para la superposición máxima, a θ = 0 (ver arriba) se establece igual a 1. Esta energía se define como eσ. El orbital metálico lleva la interacción antiunión, por lo que d z 2 es desablizado por eσ (el orbital L correspondiente se estabiliza por (β') 2 • 1 = eσ').

    Para orbitales de simetría π y δ, lo mismo se mantiene... la superposición máxima se establece igual a 1, y las energías son eπ y eδ, respectivamente.

    clipboard_ee13881d51f4f123dc20abb96f987374b.png

    E (d yz) =E (d xz) =S ML 2 (π) =eπ E (d xy) =E (d x 2 -y 2) =S ML 2 (δ) =eδ

    Al igual que con la interacción σ, la interacción (M-Lπ) * para los orbitales d es desestabilizante y el orbital basado en metal es desablizado por eπ, mientras que los ligandos Lπ son estabilizados por eπ. El mismo caso ocurre para un ligando que posee un orbital δ, siendo la única diferencia una energía de estabilización de eδ para el orbital Lδ y la energía de desestabilización de eδ para los orbitales basados en metales δ.

    S ML (δ) es pequeño en comparación con S ML (π) o S ML (σ). Además, hay pocos ligandos con simetría orbital δ (si existen, la simetría δ surge de los sistemas pπ-de ligandos orgánicos). Por estas razones, la S ML (δ) solapamiento integral y la energía asociada no se incluye en la mayoría de los tratamientos de AOM.

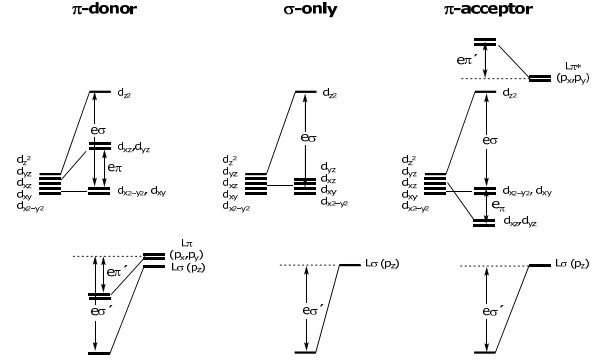
    Volviendo al problema en cuestión, los diagramas generales de nivel de energía para una molécula diatómica M-L para las tres clases de ligandos son:

    clipboard_e31b9ac0256c25d3b840ae368fa0c52dc.png

    ML 6 Complejos Octaédricos

    Por supuesto, hay más de 1 ligando en un compuesto de coordinación típico. El poder de AOM es que las energías eσ y eπ (y eδ), son aditivas. Así, los niveles de energía MO de los compuestos de coordinación se determinan simplemente sumando eσ y eπ para cada interacción M (d) -L.

    Considerar un ligando colocado arbitrariamente alrededor del metal,

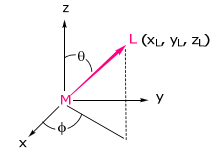
    clipboard_e3ad66cf159f3f7d409d9b918c0c6dc28.png

    Podemos imaginar colocar el ligando en el eje z metálico (con los ejes x e y de M y L también alineados) y luego girarlo sobre la superficie de una esfera (manteniendo así la distancia M-L) hasta su posición de coordenada final. Dentro del marco de referencia del ligando,

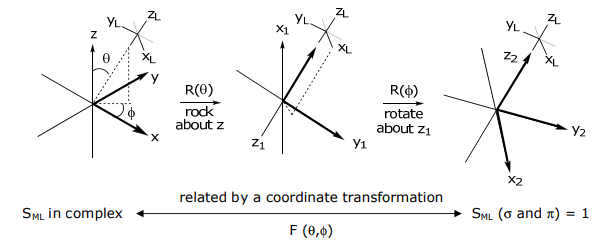
    clipboard_e63faf2a780c942a98f76a37f5b55b2f8.png

    Obsérvese que la transformación de coordenadas alinea el ligando de interés en el eje z de manera que las energías normalizadas, eσ y eπ (y eδ) puedan normalizarse a 1. La matriz de transformación para la transformación de coordenadas es:

    $$
    \ begin {array} {c|cccc}
    &\ mathbf {z} _ {2} {} ^ {2} &\ mathrm {y} _ {2}\ mathbf {z} _ {2} &\ mathrm {x} _ {2} z_ {2} &\ mathrm {x} _ {2} _ {2}\ mathrm {y} _ {2} &\ mathrm {x} _ {2} {} ^ {2} -\ mathrm {y} _ {2} {} ^ {2}
    \\ hline\ mathbf {z} ^ {\ mathbf {2}} &\ frac {1} {4} (1+3\ cos 2\ theta) & 0 & -\ frac {\ sqrt {3}} {2}\ sin 2\ theta & 0 &\ frac {\ sqrt {3}} {4} (1-\ cos 2\ theta)\
    \ mathbf {y z} &\ frac {\ sqrt {3}} {2}\ sin\ phi\ sin 2\ theta &\ cos phi\ cos\ theta &\ sin\ phi\ cos 2\ theta & -\ cos\ phi\ sin\ theta & -\ frac {1} {2}\ sin\ phi\ sin\ sin 2\ theta \\
    \ mathbf {x z} &\ frac {\ sqrt {3}} {2}\ cos\ phi\ sin 2\ theta & -\ sin\ phi\ cos\ theta &\ cos\ phi\ cos 2\ theta &\ sin\ phi\ sin\ theta & -\ frac {1} {2}\ cos\ phi\ sin 2\ theta\
    \ mathbf {x y} &\ frac {\ sqrt {3}} {4}\ sin 2\ phi (1-\ cos 2\ theta) &\ cos 2\ phi\ sin\ theta &\ frac {1} {2}\ sin 2\ phi\ sin 2\ theta &\ cos 2\ phi\ cos\ theta &\ frac {1} {4}\ sin 2\ phi (3+\ cos 2\ theta)\
    \ mathbf {x} ^ {2} -\ mathbf {y} ^ {2} &\ frac {\ sqrt {3}} {4}\ cos 2\ phi (1-\ cos 2\ theta) & -\ sin 2\ phi\ sin\ theta &\ frac {1} {2}\ cos 2\ phi\ sin 2\ theta & -\ sin 2\ phi\ cos\ theta &\ frac {1} {4}\ cos 2\ phi (3+\ cos 2\ theta)
    \ end {array}
    $$

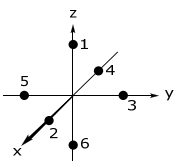
    clipboard_eb51ba52fcd090f608788ad6e50927b31.png

    \ (
    \ begin {array} {c|cccccc}
    \ text {Ligando} & 1 & 2 & 3 & 4 & 5 & 6\
    \ hline\ theta & 0 & 90 & 90 & 90 & 90 & 180 & 180^ {\ circ}\\
    \ phi & 0 & 0 & 90 & 180 & 270 & 0
    \ end { matriz}
    \)

    Considere el solapamiento del Ligando 2 en el espacio de coordenadas transformado; se debe considerar la contribución del solapamiento del Ligando 2 con cada orbital metálico. Esta interacción orbital viene dada por la matriz de transformación anterior. Al sustituir el q = 90 y φ = 0 para el Ligando 2 en la matriz de transformación anterior, se encuentra,

    para d z 2 para L 2

    \ (\ begin {alineado}
    \ mathrm {d} _ {z^ {2}} &=\ frac {1} {4} (1+3\ cos 2\ theta) d_ {z_ {2} {} {} ^ {2}} +0 d_ {y_ {2} z_ {2}} -\ frac {\ sqrt {3}} {2}\ sin 2\ theta d_ {x_ {2} z_ {2}} +0 d_ {x_ {2} y_ {2} +\ frac {\ sqrt {3}} {4} (1-\ cos 2\ theta) d_ {x_ {2} ^ {2} -y_ {2} ^ {2} ^ {2}}\
    &=-\ frac {1} {2} d_ {z_ {2} ^ {2}} +0 d_ {y _ {2} z_ {2}} +0 d_ {x_ {2} z_ {2}} +0 d_ {x_ {2} y_ {2}} +\ frac {\ sqrt {3}} {2} d_ {x_ {2} ^ {2} -y_ {2} ^ {2}}
    \ final {alineado}\)

    Así, el orbital d z 2 en la coordenada transformada, d z2 2, tiene una contribución de d z 2 y d x 2 —y 2. Recordemos que la energía de la órbita se define por el cuadrado de la integral de superposición. Así, los coeficientes anteriores son cuadrados para dar la energía del orbital dz 2 como resultado de su interacción con el Ligando 2 para ser,

    \ (
    \ mathrm {E}\ left (\ mathrm {d} _ _ {z^ {2}}\ derecha) ^ {\ mathrm {L} 2} =\ mathrm {S} _ {\ mathrm {ML}} {} ^ {2} (\ sigma) =\ beta\ cdot\ mathrm {F} _ _ {\ sigma} ^ {2} (\ theta,\ phi) =\ frac {1} {4}\ mathrm {~d} _ {\ mathrm {z} _ {2} {} ^ {2}} +\ frac {3} {4}\ mathrm {~d} _ {\ mathrm {x} _ {2} {} ^ {2} -\ mathrm {y} _ {2} {} {} ^ {2}} =\ frac {} {4}\ mathrm {e}\ sigma+ \ frac {3} {4}\ mathrm {e}\ delta\)

    Visualmente, este resultado es lógico. En la transformación de coordenadas, un ligando σ que reside en el eje z (de energía eσ) se solapa con d z 2. Esta es la energía para L1. La energía normalizada para L2 es su superposición con la coordenada transformada d z 2 2:

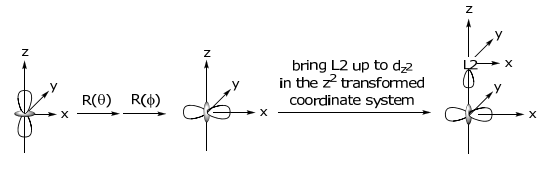
    clipboard_eec609a633f7cfe5bf3df5bf8b43ea620.png

    Tenga en cuenta que el orbital d z 2 es en realidad 2z 2 —x 2 —y 2, que es una combinación lineal de z 2 —x 2 y z 2 —y 2. Así, en el sistema transformado de coordenadas, L2, en comparación con L1, está observando la contribución x 2 de la función de onda a la unión σ. Dado que es ½ la densidad electrónica de esa en el eje z, es ¼ la energía (es decir, el cuadrado del coeficiente) en el eje σ, de ahí ¼ eσ. El componente δ de la transformación proviene de la forma funcional orbital 2z 2 — (x 2 +y 2). Así, si L2 tiene un orbital de simetría δ, entonces tendrá una energía de ¾ eδ.

    Las propiedades de transformación de los otros orbitales d, ya que pertenecen al solapamiento orbital L2, pueden determinarse completando la matriz de transformación para θ = 90 y φ = 0,

    $$
    \ left [\ begin {array} {c}
    \ mathrm {d} _ {\ mathrm {z} ^ {2}}\
    \ mathrm {~d} _ {\ mathrm {yz}}\
    \ mathrm {d} _ {\ mathrm {xz}}\
    \ mathrm {d} _ {\ mathrm {xy}}\
    \ mathrm {d} {\ mathrm {x} ^ {2} -y^ {2}}
    \ end {array}\ derecha] =\ izquierda [\ begin { array} {rrrrr}
    -\ frac {1} {2} & 0 & 0 & 0 &\ frac {\ sqrt {3}} {2}\\
    0 & 0 & 0 & 0 & 0 & -1 &
    0 & 0 & -1 & 0 & 0 &
    0 & 0 & 0 & 0 & 0 & 0\
    \ frac {\ sqrt {3}} {2} & 0 & 0 & 0 & amp;\ frac {1} {2}
    \ end {array}\ derecha]\ izquierda [\ begin {array} {c}
    \ mathrm {d} _ {z_ {2} {} {} ^ {2}}
    \\ mathrm {~d} _ {\ mathrm {y} _ {2} z_ {2}}\
    \ mathrm {~d} _ {\ mathrm {x} _ {2}\ mathrm {z} _ {2}}\\
    \ mathrm {~d} _ {\ mathrm {x} _ {2} y_ {2}}\\
    \ mathrm { ~d} _ {\ mathrm {x} _ {2} ^ {2} -\ mathrm {y} _ {2} {} ^ {2}}
    \ end {array}\ derecha]
    \]

    La contribución de energía de L2 a los niveles d-orbitales definidos por AOM es,

    \ (
    \ mathrm {E}\ izquierda (\ mathrm {d} _ {\ mathrm {yz}}\ derecha) =\ mathrm {e}\ delta;\ quad\ mathrm {E}\ izquierda (\ mathrm {d} _ {\ mathrm {xz}}\ derecha) =\ mathrm {e}\ pi;\ quad\ mathrm {E}\ izquierda (\ mathrm {d} _ {\ mathrm {xy}}\ derecha) =\ mathrm {e}\ pi;\ quad\ mathrm {E}\ izquierda (\ mathrm {d} _ {x^ {2} -y^ {2}}\ derecha) =\ frac {3} {4}\ mathrm {e}\ sigma+\ frac {1} {4}\ mathrm {e}\ delta
    \)

    Hasta este punto, solo se ha tratado el ligando L2. También es necesario determinar el solapamiento de los orbitales d con los otros cinco ligandos. Los elementos de las matrices de transformación para estos ligandos son,

    \ (
    L_ {1}:\ left [\ begin {array} {lllll}
    1 & 0 & 0 & 0 & 0 & 0 & 0 &
    0 & 0 & 0 & 0 & 0 &
    0 & 0 & 1 & 0 & 0 & 0 &
    0 & 0 & 0 & 0 & 0 & 0 &
    0 & 0 & 0 & 0 & 0 & 1
    \ end {array}\ derecha]\ quad L_ {3}:\ left [\ begin {array} {rrrrr}
    -\ frac {1} {2} & 0 & 0 & 0 &\ frac {\ sqrt {3}} {2}\
    0 & 0 & -1 & 0 & 0 & 0 &
    0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\

    -\ frac {\ sqrt {3}} {2} & 0 & 0 & 0 & -\ frac {1} {2}
    \ end {array}\ derecha]\ quad L_ {4}:\ left [\ begin {array} {ccccc}
    -\ frac {1} {2} & 0 & 0 & 0 &\ frac {\ sqrt {3}} {2}\ &
    0 & 0 & 1 & 0\\
    0 & 0 & 1 & 0 & 0\\
    0 & 1 & 0 & 0 & 0 & 0
    \\ frac {\ sqrt {3}} {2} & 0 & 0 &\ frac {1} {2}
    \ end {array}\ derecha]
    \)

    \ (
    \ mathrm {L} _ {5}:\ left [\ begin {array} {rrrrr}
    -\ frac {1} {2} & 0 & 0 &\ frac {\ sqrt {3}} {2}\
    0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 &
    0 & 0 & 0 & -1 & 0\\
    0 & -1 & 0 & 0 & 0 & 0\
    -\ frac {\ sqrt {3}} {2} & 0 & 0 & -\ frac {1} {2}
    \ end {array}\ derecha]\ quad L_ {6}:\ left [\ begin {array} {rrrrr}
    1 & 0 & 0 & 0 & 0 & 0\\
    0 & -1 & 0 & 0 & 0\\ 0 &
    0 & 1 & 0 & 0 & 0 & 0 &
    0 & 0 & 0 & 0 & 0 & 0 & 0 &
    0 & 0 & 0 & 0 & 0 & 0 & 0
    \ end {array}\ derecha]
    \)

    Al cuadrar los coeficientes para cada uno de los ligandos y luego sumar la energía total de cada d-orbital,

    $$
    \ begin {array} {lccccccc}
    \ hline &\ text {L1} &\ text {L2} &\ text {L3} &\ text {L4} &\ text {L5} &\ text {L6} &\ text {E_TOTAL}\
    \ hline\ mathbf {E}\ left (\ mathbf {d} _ {\ mathbf {z} ^ {2}}\ derecha) &\ texto {eo} &\ frac {1} {4} \ mathrm {e}\ sigma+\ frac {3} {4}\ mathrm {e}\ delta &\ frac {1} {4}\ mathrm {e}\ sigma+\ frac {3} {4}\ mathrm {e}\ delta &\ frac {1} {4}\ mathrm {e}\ sigma+\ frac {3} {4} mathrm {e}\ delta &\ frac {1} {4}\ mathrm {e}\ sigma+\ frac {3} {4}\ mathrm {e}\ delta &\ mathrm {e}\ sigma & =3\ mathrm {e}\ sigma+3\ mathrm {e}\ delta\\
    \ mathbf {E}\ izquierda (\ mathbf {d} _ {\ mathrm {yz}}\ derecha) &\ mathrm {e}\ pi &\ mathrm {e}\ delta &\ mathrm {e}\ pi &\ mathrm {e}\ delta &\ mathrm {e}\ pi &\ mathrm {e}\ pi & =4\ mathrm {e}\ pi+2\ mathrm {e}\ delta\\
    \ mathbf {E}\ izquierda (\ mathbf {d} _ {\ mathrm {xz}}\ derecha) &\ mathrm {e}\ pi &\ mathrm {e}\ pi &\ mathrm {e}\ delta &\ mathrm {e}\ pi &\ mathrm {e}\ delta &\ mathrm {e}\ pi & =4\ mathrm {e}\ pi+2\ mathrm {e}\ delta\
    \ mathbf {E}\ left (\ mathbf {d} _ {mathrm {xy}}\ derecha) &\ mathrm {e}\ delta &\ mathrm {e}\ pi &\ mathrm {e}\ pi & \ mathrm {e}\ pi &\ mathrm {e}\ pi &\ mathrm {e}\ delta & =4\ mathrm {e}\ pi+2\ mathrm {e}\ delta\
    \ mathbf {E}\ izquierda (\ mathbf {d} _ {\ mathbf {x} ^ {2} -\ mathbf {y} ^ {2}}\ derecha) &\ mathrm {e}\ delta &\ frac {3} {4}\ mathrm {e}\ sigma+\ frac {1} {4}\ mathrm {e}\ delta &\ frac {3} {4}\ mathrm {e}\ sigma+ \ frac {1} {4}\ mathrm {e}\ delta &\ frac {3} {4}\ mathrm {e}\ sigma+\ frac {1} {4}\ mathrm {e}\ delta &\ frac {3} {4}\ mathrm {e}\ sigma+\ frac {1} {4}\ mathrm {e}\ delta y mathrm {e}\ delta y mathrm rm {e}\ delta & =3\ mathrm {e}\ sigma+3\ mathrm {e}\ delta\
    \ hline
    \ end {array}
    \]

    Como se mencionó anteriormente, eδ << e σ o e π... así e δ puede ignorarse. El diagrama de nivel de energía de O h es:

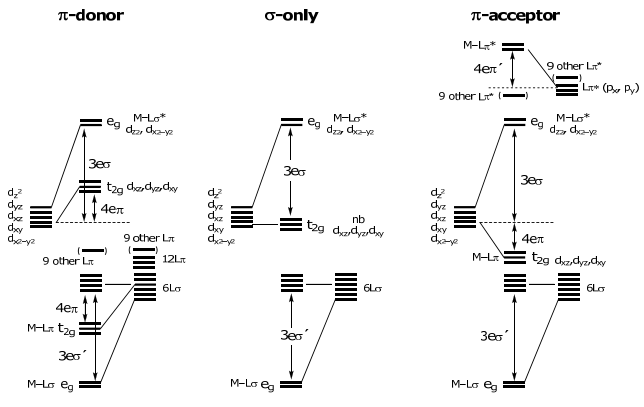
    clipboard_efaebcee12387b33b5c3c16f48ffca1da.png

    Tenga en cuenta que la división orbital d es el mismo resultado obtenido del modelo de teoría de campo cristalino (CFT) enseñado en química de primer año. De hecho, la parametrización de energía escala directamente entre CFT y AOM

    10 Dq = Δ0 = 3eσ — 4eπ

    This page titled 1.14: Método de superposición angular y diatómica M-L is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Daniel Nocera via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.