2.2: Factores geométricos que rigen la unión y la estructura

Última actualización
Guardar como PDF

Page ID: 71777

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dos parámetros, los radios y el poder de atracción de electrones de átomos o iones, determinan la unión, estructura y reacción de sustancias y compuestos elementales. Se ha dedicado mucho esfuerzo a encontrar valores numéricos para estos dos factores aplicables a todos los materiales. Se espera que las propiedades químicas de un compuesto conocido, y de un nuevo material aún inexistente, puedan predecirse con una combinación de valores numéricos adecuados. En primer lugar, se describirán los factores geométricos.

Cuadro Radios$\PageIndex{1}$ atómicos (pm)
H 32
Li 123	Ser 89											B 82	C 77	N 75	O 73	F 72
Na 154	Mg 136											Al 118	Si 111	P 106	S 102	Cl 99
K 203	Ca 174	Sc 144	Ti 132	V 122	Cr 118	Mn 117	Fe 117	Co 116	Ni 115	Cu 117	Zn 125	Ga 126	Ge 122	Como 120	Se 117	Br 114
Rb 216	Sr 191	Y 162	Zr 145	Nb 134	Mo 130	Tc 127	Ru 125	Rh 125	Pd 128	Ag 134	Cd 148	En 144	Sn 140	Sb 140	Te 136	I 133
Cs 235	Ba 198	La 169	Hf 144	Ta 134	W 130	Re 128	Os 126	Ir 127	Pt 130	Au 134	Hg 149	Tl 148	Pb 147	Bi 146

Radios atómicos e iónicos

La densidad electrónica en los átomos se acerca gradualmente, pero nunca alcanza, cero a medida que aumenta la distancia desde el núcleo. Por lo tanto, estrictamente hablando el radio de un átomo o ion es indeterminable. Sin embargo, es posible determinar la distancia de enlace entre núcleos atómicos experimentalmente. Los radios atómicos determinados experimentalmente son uno de los parámetros atómicos más importantes que describen la química estructural de los compuestos. Es razonable definir el radio metálico de un metal a granel como la mitad de la distancia entre los átomos metálicos. La mitad de la distancia entre átomos se define también como el radio covalente de una sustancia elemental covalente (Tabla$\PageIndex{1}$).

Tabla Radios$\PageIndex{2}$ iónicos (en pm) . *
Li ⁺ (4) 59	Ser ² ⁺ (4) 27	B ³⁺ (4) 11	N ³⁺ (6) 16	O ^2- (6) 140	F ^- (6) 133
Na ⁺ (6) 102	Mg ² ⁺ (6) 72	Al ³ ⁺ (6) 54	P ³⁺ (6) 44	S ^2- (6) 184	Cl ^- (6) 181
K ⁺ (6) 138	Ca ² ⁺ (6) 100	Ga ³ ⁺ (6) 62	Como ³ ⁺ (6) 58	Se ² ^- (6) 198	Br ^- (6) 196
Rb ⁺ (6) 152	Sr ² ⁺ (6) 118	En ³ ⁺ (6) 80		Te ^2- (6) 221	I ^- (6) 220
Cs ⁺ (6) 167	Ba ² ⁺ (6) 135	Tl ³ ⁺ (6) 89

*Los números entre paréntesis son el número de coordinación de los iones.

Dado que los cationes y aniones de diferentes elementos en un compuesto iónico están unidos por interacciones electrostáticas, la distancia de enlace es la suma de los radios iónicos asignados al catión y anión. El radio iónico estándar de una especie se fija primero y luego se resta de la distancia entre los iones para decidir el radio del ion compañero. Como estándar, el radio del ion O ^2- en varios óxidos se establece en 140pm (1 pm = 10 ^-12 m) (R. D. Shannon). Los radios catiónicos en óxidos son la diferencia entre la distancia de unión y 140pm. Después de decidir los radios catiónicos en óxidos, se pueden calcular otros radios aniónicos restando los radios catiónicos de las distancias entre los átomos en los compuestos iónicos. Al aplicar tales métodos a muchos compuestos iónicos, los radios iónicos se han compilado de tal manera que los valores experimentales y calculados son generalmente consistentes (Tabla$\PageIndex{2}$).

Incluso los compuestos iónicos tienen alguna contribución covalente y no se espera que las distancias de enlace calculadas y experimentales coincidan exactamente. Incluso si se cambia el radio iónico asignado a un ion estándar, aún podemos compilar un conjunto de radios iónicos que son consistentes en muchos compuestos. Otros ejemplos de los radios propuestos del ion O ^2- son 132pm (V. M. Goldschmidt) o 60 pm (J. C. Slater). También debemos tener en cuenta que las distancias catión-anión del mismo par iónico se hacen mayores a medida que aumenta el número de coordinación de iones opuestos. Por lo tanto, en cualquier discusión sobre las características estructurales de los compuestos iónicos desde el punto de vista de los radios iónicos, se debe utilizar un conjunto de radios iónicos calculados utilizando el mismo radio estándar para los compuestos con el mismo número de coordinación.

Ejercicio$\PageIndex{2}$

¿Qué radio iónico es mayor, Cs ⁺ o F ^-?

Contestar: Cs ⁺ (167pm) > F ^- (133pm). El radio del anión no siempre es mayor.

Los radios metálicos y covalentes, también llamados radios atómicos, se vuelven más pequeños en el mismo periodo de la tabla periódica a medida que el grupo del elemento va hacia la derecha y luego vuelven a aumentar en el siguiente periodo. La contracción de lantánidos es responsable de que los elementos del 5to periodo (4d) tengan casi los mismos radios atómicos que los del sexto período (5d). En la tabla periódica, los elementos lantánidos se insertan antes de los elementos 5d. Los radios atómicos de los elementos lantánidos disminuyen notablemente a medida que aumenta la carga nuclear efectiva debido a que los efectos de cribado de los orbitales 4f de los elementos lantánidos son débiles debido a sus formas orbitales. En consecuencia, los radios atómicos de los elementos que siguen a lantánidos son muy similares a los de los elementos 4d.

Entalpía de celosía

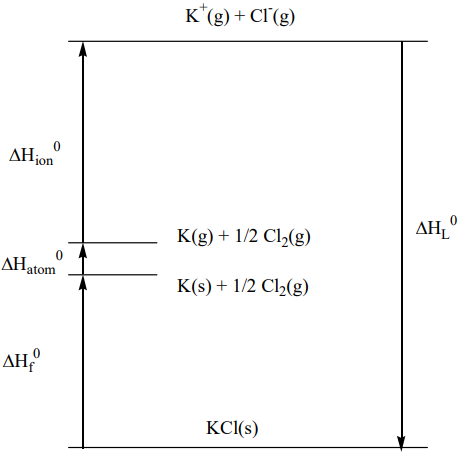
Aunque la estabilidad de un cristal a temperatura y presión constantes depende del cambio de energía libre de Gibbs de la formación del cristal a partir de sus iones constituyentes, la estabilidad de un cristal está determinada principalmente por el cambio de entalpía solo ya que la formación de la red es muy exotérmica, y el término entropía es insignificante (refiérase a la Sección 3.1). La entalpía reticular,$\Delta H_L$, se define como el cambio de entalpía estándar de la reacción en la que un cristal iónico se descompone en iones gaseosos (s es sólido, g es gas y L es retícula).

\[MX(s) \rightarrow M^{+} (g) + X^{-} (g) \qquad \Delta H_{L}\]

La entalpía de celosía se calcula indirectamente a partir de los valores del cambio de entalpía en cada etapa usando un ciclo Born-Haber (Figura$\PageIndex{1}$). A saber, se forma un ciclo cerrado utilizando datos de entalpía; entalpía estándar de formación$\Delta H_f$ de un cristal iónico a partir de elementos, entalpía de sublimación de un sólido elemental, o entalpía$\Delta\H_atom corresponding to the dissociation enthalpy of a gaseous elementary molecule, the ionization enthalpy \(\Delta$ de atomización, _ion N, que es la suma de la entalpía de ionización de la formación de cationes y electrones entalpía de adquisición de la formación de aniones. La entalpía de celosía se calcula usando la relación de que el cambio de entalpía en un ciclo es cero.

\[\Delta H_{atom}^{0} + \Delta_{ion}^{0} - \Delta H_{L}^{0} - \Delta H_{f}^{0} = 0\]

Figura$\PageIndex{1}$: - Ciclo Nacido-Haber de KCl

Constante de Madelung

La energía potencial total de Coulomb que existe entre los iones en un cristal iónico constituido por los iones A y B debe ser la suma de las energías potenciales de Coulomb individuales V _ab. Dado que las ubicaciones de los iones en la red cristalina se deciden por el tipo de estructura, el potencial de Coulomb total entre todos los iones se calcula ajustando la distancia entre los iones a d. A es la constante de Madelung que es característica de cada tipo de cristal (Tabla$\PageIndex{3}$) .

\[V = N_{A} \frac{e^{2}}{4 \pi \epsilon_{0}} \left(\dfrac{z_{A} z_{B}}{d} \right) \times A\]

N _A es la constante de Avogadro y z _A y z _B son las cargas eléctricas del catión y anión. La interacción electrostática entre iones contiguos es la más fuerte, y la constante de Madelung generalmente se vuelve más grande a medida que aumenta el número de coordinación. Debido a que las cargas eléctricas tienen signos opuestos, el potencial se vuelve negativo, lo que indica la estabilización que acompaña a la formación de una red cristalina a partir de iones en fase gaseosa bien dispersos. Si bien en general es cierto que el menor potencial electrostático conduce a la estructura más estable, esto no es estrictamente correcto ya que también hay otras interacciones a considerar.

Constantes de tabla de$\PageIndex{3}$ Madelung
Tipo estructural	A
Sal de roca	1.748
Cloruro de cesio	1.763
Esfalerita	1.638
Wurtzita	1.641
Fluorita	2.519
Rutilo	2.408

El segundo factor más importante que contribuye a la entalpía reticular es la fuerza de van der Waals, y las fuerzas de dispersión o la interacción de Londres son el origen principal de esta fuerza. Se trata de una interacción atractiva entre dipolos eléctricos, que es inversamente proporcional a la sexta potencia de la distancia d entre iones. La fuerza de van der Waals es muy pequeña.

\[V = - \frac{N_{A} C}{d^{6}}\]

El valor de la constante C es una función de cada compuesto. Dado que es como máximo 1% de la fuerza coulómbica, se puede descuidar de manera segura en el cálculo de la entalpía de celosía.

d) Estructura de cristales metálicos

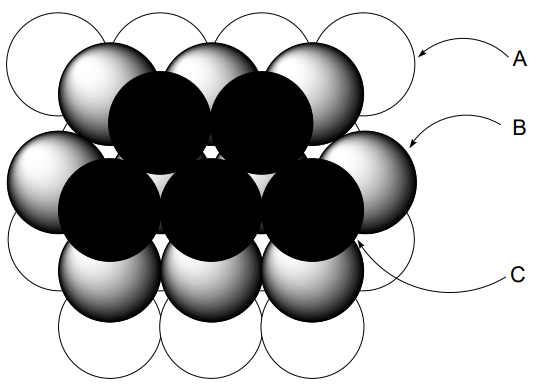
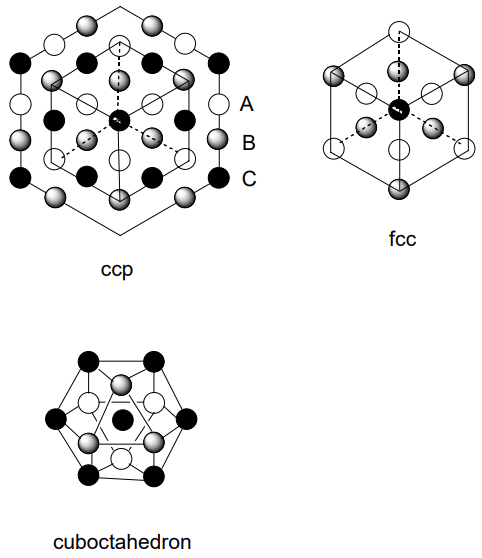
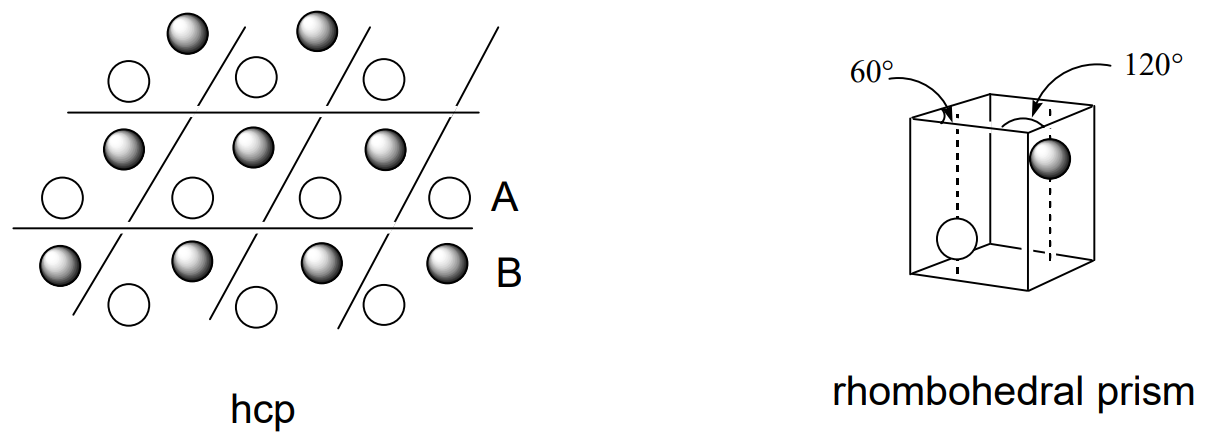
Si imaginamos que los átomos metálicos son bolas duras, cuando están densamente empaquetadas en dos dimensiones cada bola estará en contacto con otras seis bolas (A). Cuando otra capa de esta disposición bidimensional se coloca encima de la primera, el empaque será más denso y la estructura más energéticamente estable cuando los átomos metálicos se coloquen en la parte superior de los huecos (B) de la primera capa. Cuando se coloca una tercera capa encima de la 2da capa, hay dos posibilidades. Es decir, la tercera capa (A) se solapa con la primera capa (A) o la tercera capa (C) no se solapa con (A) ni con (B). El ABAB... tipo empaque se llama hexagonalmente cerrado (hcp) (Figura$\PageIndex{2}$), y el ABCABC... tipo se llama cúbico cerrado (ccp) (Figura$\PageIndex{3}$). En ambos casos, cada bola está rodeada por 12 bolas, es decir, está 12 coordinadas. El poliedro de coordinación de hcp es anti-cubooctaedro,

Figura$\PageIndex{2}$: - Hexagonalmente empaquetadas (hcp) de bolas.

Figura$\PageIndex{3}$: - Cubic Close-packed (ccp) de bolas.

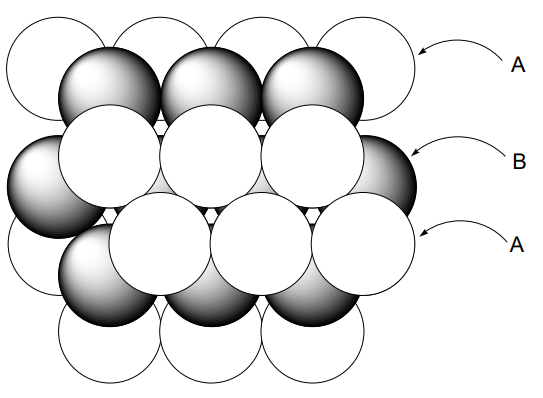
y el de ccp es cubooctaedro. Cuando la celosía se corta en diferentes planos, la celosía unitaria de ccp parece ser una celosía cúbica centrada en la cara (fcc), que contiene una bola en cada vértice cúbico y en el centro de cada cara (Figura$\PageIndex{4}$). La celosía unitaria de hcp es un prisma romboédrico en el que se ubican dos bolas en las posiciones mostradas en (Figura$\PageIndex{5}$). Existen varios modos diferentes de apilamiento de capas distintas a las normales hcp y ccp, y se conocen muchos ejemplos.

Figura$\PageIndex{4}$: - Diferentes expresiones de cúbicos empaquetados.

Figura$\PageIndex{5}$: - Diferentes expresiones de hexagonalmente empaquetados.

La celosía con otra bola en el centro de una celosía cúbica que consta de ocho bolas es la celosía cúbica centrada en el cuerpo (bcc), y algunos metales asumen este modo de empaque. La proporción de ocupación de espacio en una celosía bcc es menor que la de las compactas, pero la diferencia no es grande. A pesar de que el balón central está formalmente coordinado por 8, es esencialmente coordinado por 14 ya que hay otras seis bolas solo 15.5% más distantes que las primeras ocho bolas. Sin embargo, debido a la menor proporción de ocupación de espacio, el bcc aparece relativamente raramente y los metales puros tienden a adoptar hcp o ccp.

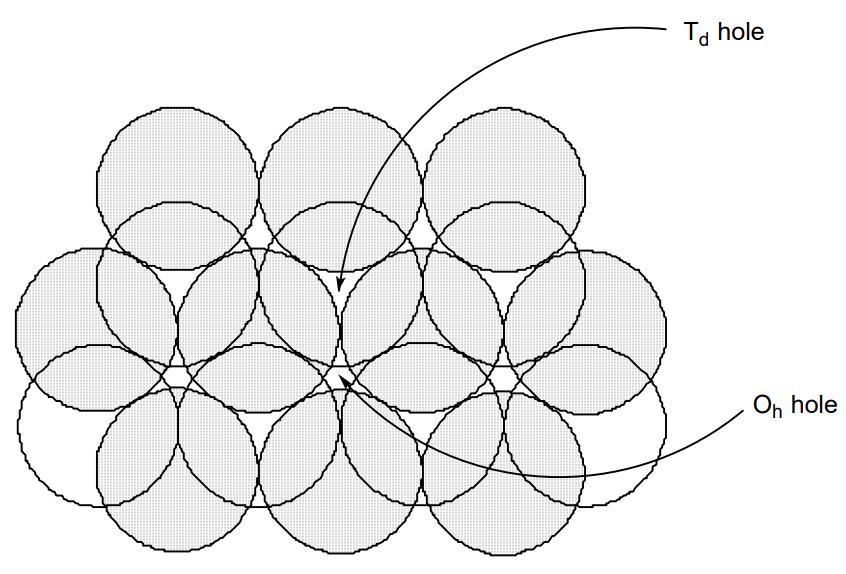
Tanto en hcp como en ccp, las cavidades entre las bolas son los orificios O _h encerrados octaédricamente por seis bolas o los orificios T _d encerrados tetraédricamente por cuatro bolas (Figura$\PageIndex{6}$). (O _h y T _d son los símbolos de simetría utilizados en la teoría de grupos.) En los sólidos iónicos, si los aniones están en arreglos hcp o ccp, los cationes entran en cualquiera de estas cavidades.

Figura$\PageIndex{6}$: - Agujeros octaédricos y tetraédricos.

Cristal Iónico

En los cristales iónicos, como haluros, óxidos y sulfuros metálicos, los cationes y aniones metálicos se alinean alternativamente, y el sólido se une principalmente por unión electrostática. Muchos haluros metálicos se disuelven en disolventes polares, por ejemplo, el cloruro de sodio NaCl se disuelve en agua; mientras que los óxidos y sulfuros metálicos, en los que hay una contribución significativa de enlace covalente, suelen ser insolubles incluso en el disolvente más polar. La estructura fundamental de los cristales iónicos es que los iones más grandes (generalmente aniones) están muy empaquetados y los iones más pequeños (generalmente cationes) entran en las cavidades octaédricas o tetraédricas entre ellos. Los cristales iónicos se clasifican en varias estructuras típicas de acuerdo con los tipos de cationes y aniones involucrados y sus radios iónicos. Cada tipo de estructura se llama por el nombre del compuesto típico, así como la estructura de sal de roca que representa las estructuras no solo de NaCl (sal de roca) sino también de varios otros compuestos. En la Tabla se muestran tipos de estructuras representativas de compuestos sólidos y ejemplos pertenecientes a cada tipo$\PageIndex{4}$.

Tabla Tipos de$\PageIndex{4}$ cristales de compuestos en estado sólido
Tipo de cristal	Número de coordinación	Ejemplos de compuestos
Sal de roca	(6,6)	LiCl, NaCl, KBr, RBi, AgCl, MgO, NiO, InP
Cloruro de cesio	(8,8)	CsCl, CSBr, CSi, CuZn
Esfalerita	(4,4)	ZnS, CDs, HgS, CuCl, GAP
Fluorita	(8,4)	CaF ₂, SrF ₂, CdF ₂, ZrO ₂, UO ₂
Rutilo	(6,3)	TiO ₂, SnO ₂, RuO ₂, NiF ₂
Yoduro de cadmio	(6,3)	CDI ₂, CoI ₂, Mg (OH) ₂
Óxido de renio	(6,2)	ReO ₃, WO ₃, Sc (OH) ₃
Perovskita	(6,2)	CaTiO ₃, BaTiO ₃, SrTiO ₃

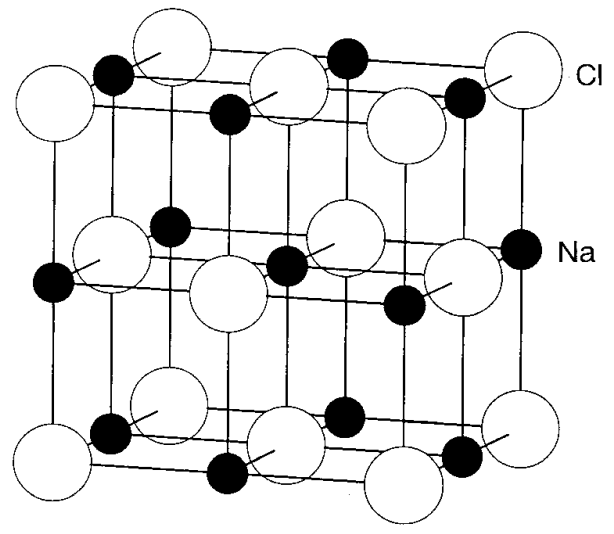
Estructura roca-sal El cloruro de sodio El NaCl es un compuesto típico en el que los aniones Cl- se disponen en ccp y los cationes Na+ ocupan todos los agujeros octaédricos (Oh holes) (Figura$\PageIndex{7}$). Cada catión Na+ está rodeado por seis aniones Cl-. La misma estructura resulta incluso si se intercambian las posiciones de aniones y cationes. En el caso de la estructura invertida, cada anión Cl- está rodeado por seis cationes Na+. A saber, cada ion es 6-coordinado y es conveniente describir la estructura como la estructura (6,6). El número de iones en una red unitaria se calcula sumando los iones mostrados en la Figura$\PageIndex{7}$. Dado que hay un ion dentro de la red, los iones en las caras de la red son compartidos por 2, en los bordes por 4, y en las esquinas por 8 celosías, se obtiene una red de 4 iones Cl pertenecientes a la red unitaria de NaCl multiplicando los números de iones dentro de la red por 1, en las caras por 1/2, en los bordes por 1/4 y en las esquinas por 1/8. El número de iones Na en la red unitaria también es 4 y la relación de iones Cl y Na concuerda con la fórmula NaCl.

Figura$\PageIndex{7}$: - Estructura de sal de roca.

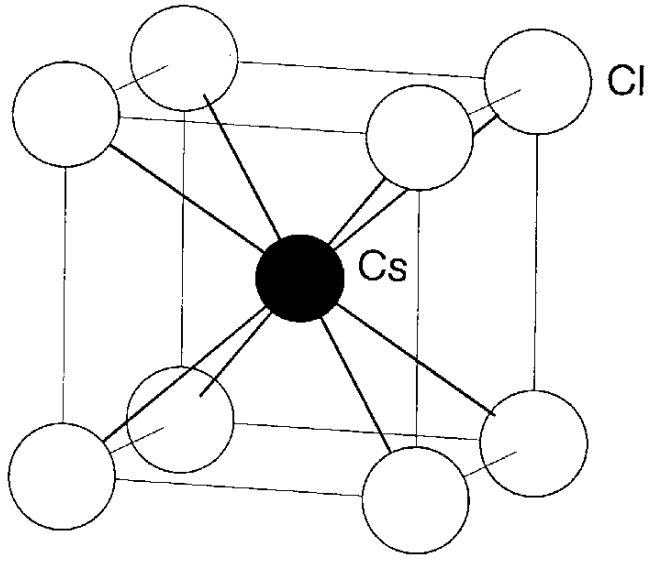
Estructura del cloruro de cesio El cloruro de cesio, CsCl, es un ejemplo típico de la estructura mostrada en la Figura$\PageIndex{8}$. Hay un ion Cs ⁺ en el centro y ocho Cl ^- se encuentran en las ocho esquinas del cubo. Por el contrario, aunque un Cl ^- llegue al centro y ocho Cs ⁺ lleguen a las esquinas, el número de cada ion en la celosía unitaria es el mismo. Así, a esto se le conoce como la (8, 8) -estructura. Dado que hay un Cs ⁺ y un ion Cl ^- pertenecientes a esta red unitaria, coincide con la fórmula CsCl.

Figura$\PageIndex{8}$: - Estructura de cloruro de cesio

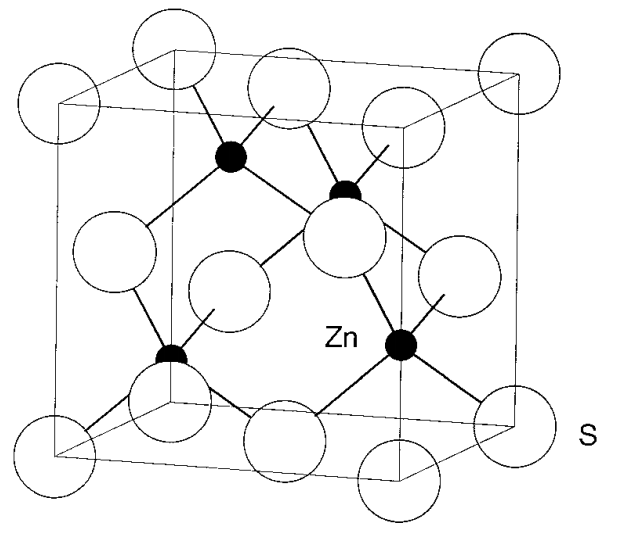
Estructura de la blenda de zinc La blenda de zinc tiene la composición ZnS y su red unitaria se muestra en la Figura$\PageIndex{9}$. Los aniones S ^2- están dispuestos en ccp y los cationes Zn ² ⁺ ocupan la mitad de los agujeros tetraédricos (agujeros Td). En esta disposición, cada catión está coordinado por cuatro aniones, y cada anión por cuatro cationes. De ahí que se trate de una estructura (4, 4). Hay cuatro iones Zn ² ⁺ y S ^2- pertenecientes a esta red unitaria y la relación atómica coincide con la fórmula de ZnS.

Figura$\PageIndex{9}$: - Estructura de blenda de zinc.

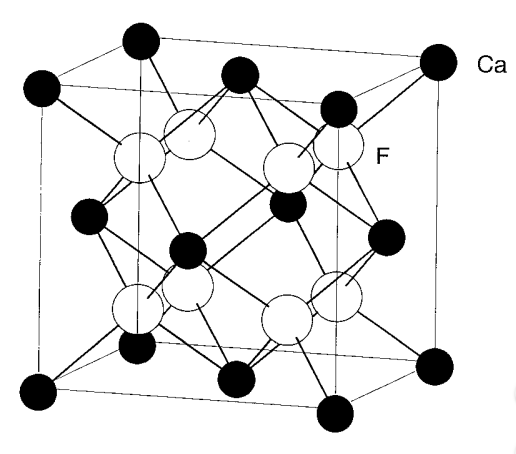
Estructura de fluorita La composición de la fluorita es CaF ₂. Dado que el número de F ^- es el doble que el de Ca ²⁺, todos los agujeros tetraédricos de Ca ²⁺ dispuestos en ccp están ocupados por F ^-, como se muestra en la Figura$\PageIndex{10}$. Hay cuatro iones Ca ²⁺ y ocho F ^- y el número de iones es 4 veces la fórmula. La estructura anti-fluorita intercambia los cationes y aniones, y se ejemplifica por el óxido de potasio K ₂ O, etc.

Figura$\PageIndex{10}$: - Estructura de fluorita.

Ejercicio$\PageIndex{3}$

¿Cuántos cationes y aniones hay en una celosía unitaria de estructura de blenda de zinc?

Contestar: Los cuatro cationes están incluidos en una celosía unitaria. Los aniones ocupan las 8 esquinas y 6 caras y el número es de 8 x 1/8 + 6 x 1/2 = 4.

Relación de radio

Generalmente, la energía potencial coulómbica total E _c del compuesto iónico univalente MX se expresa mediante la siguiente fórmula.

\[E_{c} = - \frac{N_{A} e^{2}}{4 \pi \epsilon_{0} R} A\]

N _A es la constante de Avogadro, A la constante de Madelung y R la distancia entre iones. De acuerdo con esta fórmula, una estructura con una relación A/R mayor es más estable. La constante de Madelung de un compuesto MX aumenta al aumentar el número de coordinación. Por otro lado, es ventajoso disminuir el número de coordinación y reducir R en el caso de M pequeña, dificultando el contacto entre M y X. En un cristal iónico, la relación de r _M y r _X con los aniones en contacto entre sí y también con los cationes depende del número de coordinación.

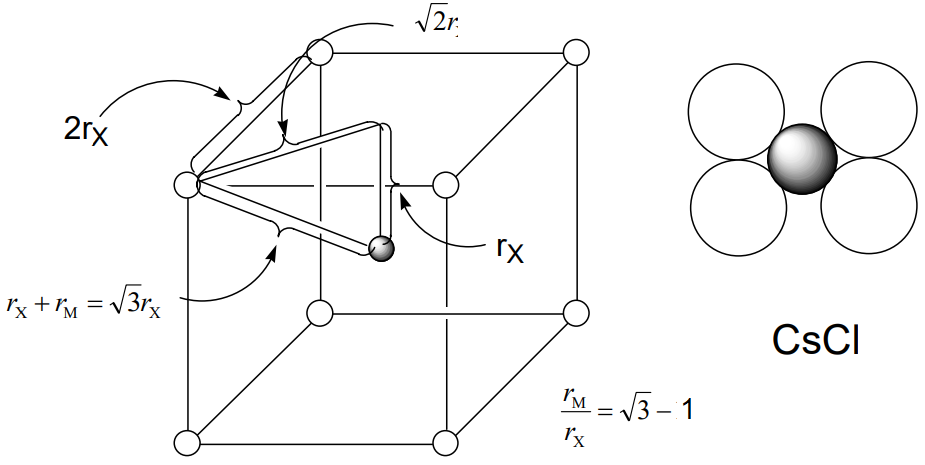
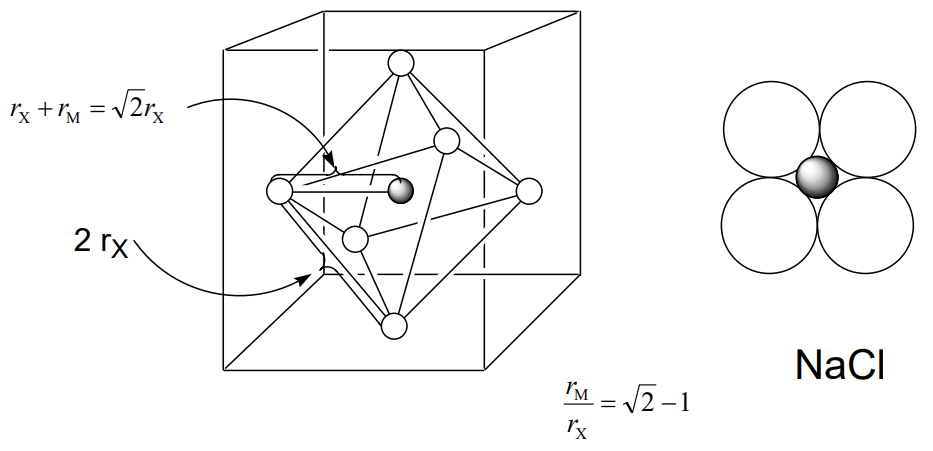
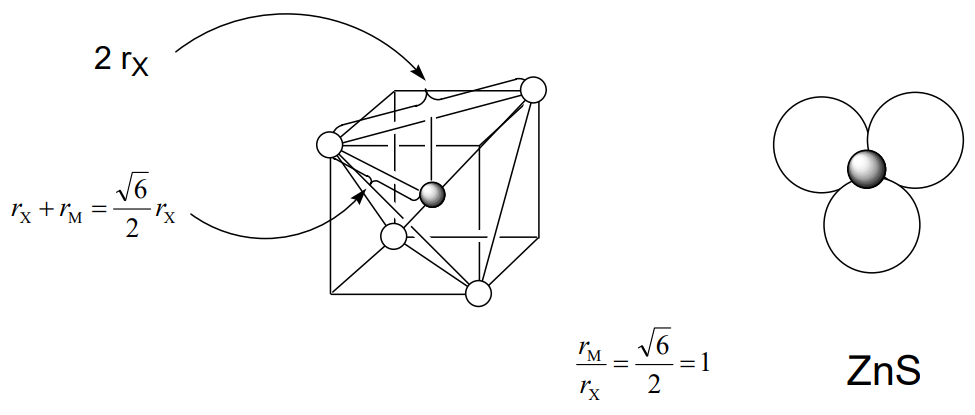
En una estructura parcial que consiste únicamente en aniones, los aniones forman un poliedro de coordinación alrededor de un catión. El radio aniónico rX es la mitad de la distancia del borde del poliedro y la distancia desde el centro catiónico a un ápice del poliedro es la suma de los radios aniónicos y catiónicos r _X + r _M. El poliedro de coordinación de la estructura CsCl es un cubo, la estructura NaCl un octaedro y la ZnS estructura un tetraedro. La distancia desde el centro de cada poliedro a un ápice es$\sqrt{3} r_{X}$$\sqrt{2} r_{X}$,,\ frac {\ sqrt {6}} {2} r_ {X}\). Por lo tanto, las proporciones de los radios catiónicos y aniónicos r _M/r _X son $$\ frac {\ sqrt {3} r_ {X} − r_ {X}} {r_ {X}} =\ sqrt {3} −1 = 0.732$$para CsCl, $$\ frac {\ sqrt {2} r_ {X} − r_ {X}} {r_ {X}}} =\ sqrt {2} −1 = 0.414$$para NaCl, y $$\ frac {\ frac {\ sqrt {6}} {2} r_ {X} - r_ {X}} {r_ {x}} =\ frac {\ sqrt {6}} {2} - 1 = 0.225$$para estructuras ZnS (Figura$\PageIndex{11}$).

Se ha explicado que el número de coordinación disminuye cuando estas relaciones de radio son menores que los valores dados ya que los cationes y aniones no entran en contacto entre sí, provocando inestabilidad. Por otro lado, el número de coordinación aumenta para cationes más grandes, incrementando la relación de radio. Sin embargo, la relación entre un número de coordinación y una relación de radio no es simple. Por ejemplo, los haluros de metales alcalinos adoptan las estructuras de NaCl a temperaturas normales excepto cloruro de cesio CsCl, bromuro de cesio CsBr y yoduro de cesio CSi. No es posible asumir tipos de estructura a partir de las relaciones de radio incluso en el caso de compuestos iónicos simples como haluros de metales alcalinos. Sin embargo, la tendencia cualitativa de que los cationes más pequeños tienen números de coordinación más pequeños es generalmente correcta.

Figura$\PageIndex{11}$: - La relación de radio r _M/r _X de cationes y aniones.

Variación de la expresión de la estructura sólida

Muchos compuestos inorgánicos en estado sólido tienen estructuras tridimensionales complicadas. Diferentes ilustraciones estructurales para un mismo compuesto ayudan a comprender su estructura. En el caso de compuestos inorgánicos complicados, trazar líneas de enlace entre átomos, como en la mayoría de los compuestos orgánicos, causa confusión. Los aniones en muchos óxidos metálicos, sulfuros o haluros forman tetraedros u octaedros alrededor de los cationes metálicos centrales. Aunque no hay enlace entre los aniones, las estructuras se simplifican enormemente si se ilustran por los poliedros aniónicos que comparten ápices, bordes o caras. En tales ilustraciones, generalmente se omiten los átomos metálicos catiónicos. Como se ha mencionado, las estructuras sólidas iónicas pueden ser consideradas como un conjunto de aniones empaquetados muy cerca.

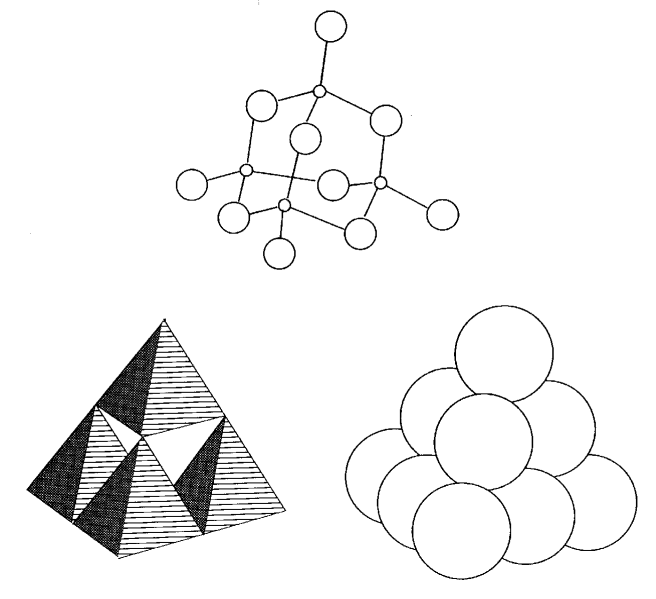
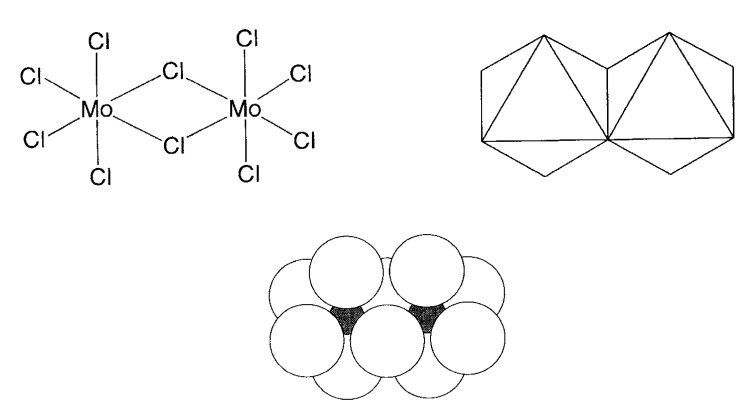
Las figuras 2.12 y 2.13 ilustran estas tres representaciones para pentóxido de fósforo molecular P ₂ O ₅ (= P ₄ O ₁₀) y pentacloruro de molibdeno MoCl ₅ (= Mo ₂ Cl ₁₀). Las representaciones poliédricas son mucho más fáciles de entender para las estructuras de moléculas grandes o compuestos de estado sólido formados por un número infinito de átomos. Sin embargo, la representación de la línea de enlace es adecuada para compuestos moleculares tales como los ejemplos anteriores.

Figura$\PageIndex{12}$: - Tres expresiones para la estructura de P ₄ O ₁₀.

Figura$\PageIndex{13}$: - Tres expresiones para la estructura de Mo ₂ Cl ₁₀.