Saltar al contenido principal
LibreTexts Español

4.3: Propiedades y representaciones de grupos

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    81585

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Haga clic aquí para ver una conferencia sobre este tema.

    Multiplicación de Grupo

    Ahora investigaremos qué sucede cuando aplicamos dos operaciones de simetría en secuencia. Como ejemplo, considere la\(NH_3\) molécula, que pertenece al grupo\(C_{3v}\) puntual. Considera lo que sucede si aplicamos una\(C_3\) rotación (120˚ en sentido antihorario) seguida de una \(\sigma_v\)reflexión (reflexión sobre el \(\sigma_v\)eje). Escribimos esta operación combinada \(\sigma_v\)\(C_3\)(cuando se escribe, las operaciones de simetría operan sobre la cosa directamente a su derecha, tal como lo hacen los operadores en la mecánica cuántica; por lo tanto, tenemos que trabajar hacia atrás de derecha a izquierda desde la notación para obtener el orden correcto en el que el se aplican operadores). Como veremos pronto, es importante el orden en que se aplican las operaciones.

    alt

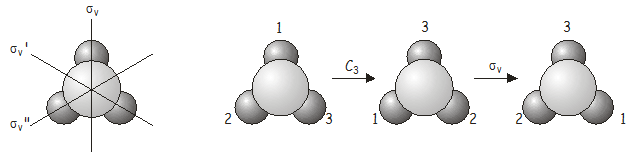
    La operación combinada \(\sigma_v\)\(C_3\)es equivalente a \(\sigma_v''\)(¡tenga en cuenta el doble prime encendido\(\sigma_v''\)!) , que también es una operación de simetría del grupo de\(C_{3v}\) puntos. Ahora veamos qué pasa si aplicamos los operadores en el orden inverso, es decir,\(C_3\)\(\sigma_v\) is (\(\sigma_v\)seguido de \(C_3\)).

    alt

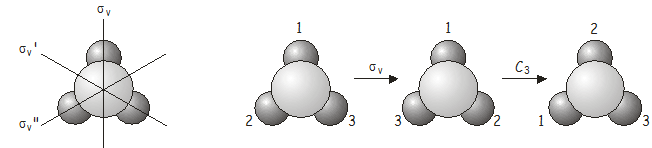
    Nuevamente, la operación combinada\(C_3\)\(\sigma_v\) equivale a otra operación del grupo de puntos, esta vez \(\sigma_v'\)(¡anote el prime único encendido\(\sigma_v'\)!) .

    Hay dos puntos importantes que se ilustran con este ejemplo:

    1. El orden en que se aplican dos operaciones es importante. Para dos operaciones de simetría\(A\) y\(B\), no\(AB\) es necesariamente lo mismo que\(BA\), es decir, las operaciones de simetría no se conmutan en general. En algunos grupos los elementos de simetría sí viajan; se dice que tales grupos son abelianos.
    2. Si dos operaciones del mismo grupo de puntos se aplican en secuencia, el resultado será equivalente a otra operación del grupo de puntos. Se dice que las operaciones de simetría que están relacionadas entre sí por otras operaciones de simetría del grupo pertenecen a la misma clase. En\(NH_3\), los tres planos de espejo \(\sigma_v\), \(\sigma_v'\)y \(\sigma_v''\)pertenecen a la misma clase (relacionados entre sí a través de una\(C_3\) rotación), al igual que las rotaciones\(C_3^+\) y\(C_3^-\) (rotaciones en sentido antihorario y en sentido horario alrededor del principal eje, relacionados entre sí por un plano de espejo vertical).

    Cuatro propiedades de los grupos matemáticos

    Ahora que hemos explorado algunas de las propiedades de las operaciones y elementos de simetría y su comportamiento dentro de los grupos de puntos, estamos listos para introducir la definición matemática formal de un grupo. Las siguientes definiciones se pondrán en el contexto de la simetría molecular.

    Un grupo matemático se define como un conjunto de elementos (\(A_1\),\(A_2\),\(A_3\)...) junto con una regla para formar combinaciones\(A_i\),\(A_j\)... Para nuestros fines,,\(A_1\)\(A_2\)\(A_3\), etc. son elementos de simetría y\(A_i\),\(A_j\), etc. son operaciones de simetría descritas en una sección anterior. Los elementos del grupo y la regla para combinarlos deben cumplir los cuatro criterios siguientes.

    1. El grupo debe incluir la identidad\(E\), que conmuta con otros miembros del grupo. En otros términos, \(E A_i= A_i \)para todos los elementos del grupo. La aplicación de la operación de identidad antes o después de otra operación\(A_i\),, da como resultado el mismo resultado que\(A_i\) solo.
    2. Los elementos deben satisfacer la propiedad de grupo de que la combinación de cualquier par de elementos también es un elemento del grupo. Por ejemplo, en el grupo de\(C_{3v}\) puntos, una rotación C 3 seguida de\(\sigma_v\) a da otra operación que ya forma parte del grupo: a\(\sigma_v"\).
    3. Cada operación de simetría\(A_i\) debe tener una inversa\(A_i^{-1}\), que también es un elemento del grupo, de tal manera que\[A_i A_i^{-1} = A_i^{-1}A_i = E \nonumber \] La inversa\(g_i^{-1}\) efectivamente 'deshace' el efecto de la operación de simetría\(g_i\). Por ejemplo, en el grupo de\(C_{3v}\) puntos, la inversa de\(C_3^+\) es\(C_3^-\).
    4. La regla de combinación debe ser asociativa\[(A_i A_j )(A_k) = A_i(A_jA_k) \nonumber \] Or\(A(BC)=(AB)C\). Es decir, el orden de las operaciones no debería importar.

    La teoría de grupos es un área importante en matemáticas, y por suerte para los químicos los matemáticos ya han hecho la mayor parte del trabajo por nosotros. Junto a la definición formal de grupo viene un marco matemático integral que nos permite llevar a cabo un tratamiento riguroso de la simetría en los sistemas moleculares y conocer sus consecuencias.

    Muchos problemas que involucran operadores u operaciones (como los que se encuentran en la mecánica cuántica o la teoría de grupos) pueden ser reformulados en términos de matrices. Cualquiera de ustedes que se haya encontrado con matrices de transformación antes sabrá que las operaciones de simetría como rotaciones y reflexiones pueden estar representadas por matrices. Resulta que el conjunto de matrices que representan las operaciones de simetría en un grupo obedece a todas las condiciones establecidas anteriormente en la definición matemática de un grupo, y el uso de representaciones matriciales de operaciones de simetría simplifica la realización de cálculos en la teoría de grupos. Antes de aprender a usar matrices en la teoría de grupos, probablemente será útil revisar algunas definiciones básicas y propiedades de las matrices.

    *Esta página fue adaptada desde aquí (click).

    Colaboradores y Atribuciones

    4.3: Propiedades y representaciones de grupos is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.