4.3.1: Matrices

La simetría de las moléculas es esencial para comprender las estructuras y propiedades de los compuestos orgánicos e inorgánicos. Las propiedades de los compuestos químicos a menudo se explican fácilmente por la consideración de la simetría. Por ejemplo, la simetría de una molécula determina si la molécula tiene un momento dipolo permanente o no. Las teorías que describen la actividad óptica, la espectroscopia infrarroja y ultravioleta y la estructura cristalina implican la aplicación de consideraciones de simetría. El álgebra matricial es la herramienta matemática más importante en la descripción de la simetría.

Las propiedades de los grupos de simetría se organizan en tablas de caracteres (discutidas más adelante en este capítulo). Las tablas de caracteres se construyen a partir de matrices. Esta página es una breve descripción de las matrices y la multiplicación de matrices.

¿Qué es una matriz?

Una\(m\times n\) matriz\(\mathbf{A}\) es una matriz rectangular de números con\(m\) filas y\(n\) columnas. Los números\(m\) y\(n\) son las dimensiones de\(\mathbf{A}\). Los números en la matriz se llaman sus entradas. Se llama a la entrada en fila\(i\) y columna\(j\)\(a_{ij}\).

Figura\(\PageIndex{1}\): Matrices de diferentes dimensiones

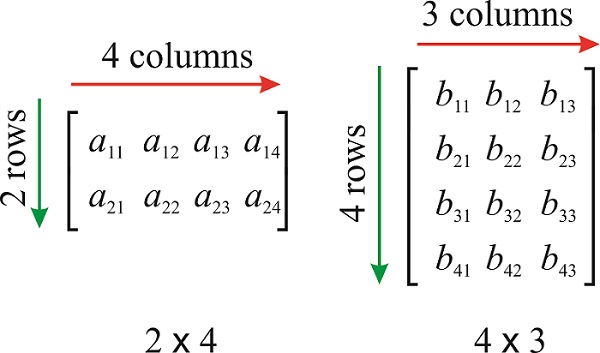
Algunos tipos de matrices tienen nombres especiales:

• Una matriz cuadrada:\[\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \\ -i & 1/2 &9 \end{pmatrix} \nonumber \] con\(m=n\)
• Una matriz rectangular:\[\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \end{pmatrix}\nonumber \] con\(m\neq n\)
• Un vector de columna:\[\begin{pmatrix} 3 \\ 5\\ -i \end{pmatrix}\nonumber \] con\(n=1\)
• Un vector de fila:\[\begin{pmatrix} 3 &-2 &4 \\ \end{pmatrix}\nonumber \] con\(m=1\)
• La matriz de identidad:\[\begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0&0 &1 \end{pmatrix}\nonumber \] con\(a_{ij}=\delta_{i,j}\), donde\(\delta_{i,j}\) es una función definida como\(\delta_{i,j}=1\) if\(i=j\) y\(\delta_{i,j}=0\) if\(i\neq j\).
• Una matriz diagonal:\[\begin{pmatrix} a &0 &0 \\ 0 &b &0 \\ 0&0 &c \end{pmatrix}\nonumber \] con\(a_{ij}=c_i \delta_{i,j}\).
• Una matriz triangular superior:\[\begin{pmatrix} a &b &c \\ 0 &d &e \\ 0&0 &f \end{pmatrix}\nonumber \] Todas las entradas por debajo de la diagonal principal son cero.
• Una matriz triangular inferior:\[\begin{pmatrix} a &0 &0 \\ b &c &0 \\ d&e &f \end{pmatrix}\nonumber \] Todas las entradas por encima de la diagonal principal son cero.
• Una matriz triangular es aquella que es triangular inferior o triangular superior.

El rastro de una matriz

El rastro de una matriz\(n\times n\) cuadrada\(\mathbf{A}\) es la suma de los elementos diagonales, y formalmente definido como\(Tr( \mathbf{A})=\sum_{i=1}^{n}a_{ii}\).

Por ejemplo,

\[\mathbf{A}=\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \\ -i & 1/2 &9 \end{pmatrix}\; ; Tr(\mathbf{A})=12+3i \nonumber \]

Matrices Singulares y No Singulares

Una matriz cuadrada con determinante distinto de cero se llama nonsingular. Una matriz cuyo determinante es cero se llama singular. (Tenga en cuenta que no se puede calcular el determinante de una matriz no cuadrada).

Para una matriz de 2x2,

\[\mathbf{B}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\; ; det(\mathbf{B})= ad - cb \nonumber \]

Para una matriz de 3x3,

\[\mathbf{C}=\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \nonumber \]

\[det(\mathbf{C})=a\begin{pmatrix} e & f \\ h & i \end{pmatrix} - b\begin{pmatrix} d & f \\ g & i \end{pmatrix} + c\begin{pmatrix} d & e \\ g & h \end{pmatrix} \nonumber \]

\[det(\mathbf{C})= aei - ahf -bdi + bgf + cdh - cge \nonumber \]

La Transpone Matrix

La transposición matricial, más comúnmente escrita\(\mathbf{A}^T\), es la matriz obtenida mediante el intercambio\(\mathbf{A}\) de filas y columnas. Se obtiene reemplazando todos los elementos\(a_{ij}\) por\(a_{ji}\). Por ejemplo:

\[\mathbf{A}=\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \end{pmatrix}\rightarrow \mathbf{A}^T=\begin{pmatrix} 3 &5\\ -2 &3i\\ 4&3 \end{pmatrix} \nonumber \]

---

Multiplicación de Matriz

Para multiplicar dos matrices, el número de columnas verticales en la primera matriz debe ser el mismo que el número de filas en la segunda matriz. Si\(\mathbf{A}\) tiene dimensiones\(m\times n\) y\(\mathbf{B}\) dimensiones\(n\times p\), entonces el producto\(\mathbf{AB}\) se define, y tiene dimensiones\(m\times p\).

\[c_{ij} = \sum a_{ij} \times b_{ij} \nonumber \]

La entrada\(a_{ij} \times b_{ij}\) se obtiene multiplicando fila\(i\) de\(\mathbf{A}\) por columna\(j\) de\(\mathbf{B}\), lo cual se realiza multiplicando las entradas correspondientes juntas y luego sumando los resultados:

Figura\(\PageIndex{1}\): Multiplicación matricial

Ejemplo\(\PageIndex{1}\)

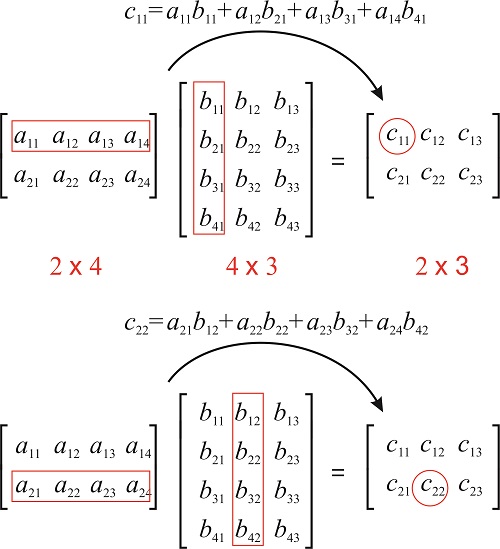
Calcular el producto

\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1 &0 \\ 5 &3 \\ -1 &0 \end{pmatrix} \nonumber \]

Solución

Necesitamos multiplicar una\(3\times 3\) matriz por una\(3\times 2\) matriz, así que esperamos una\(3\times 2\) matriz como resultado.

\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1 &0 \\ 5 &3 \\ -1 &0 \end{pmatrix}=\begin{pmatrix} a&b \\ c&d \\ e &f \end{pmatrix} \nonumber \]

Para calcular\(a\), que es entrada (1,1), usamos la fila 1 de la matriz a la izquierda y la columna 1 de la matriz a la derecha:

\[\begin{pmatrix} {\color{red}1} &{\color{red}-2} &{\color{red}4} \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} {\color{red}1} &0 \\ {\color{red}5} &3 \\ {\color{red}-1} &0 \end{pmatrix}=\begin{pmatrix} {\color{red}a}&b \\ c&d \\ e &f \end{pmatrix}\rightarrow a=1\times 1+(-2)\times 5+4\times (-1)=-13 \nonumber \]

Para calcular\(b\), que es entrada (1,2), usamos la fila 1 de la matriz a la izquierda y la columna 2 de la matriz a la derecha:

\[\begin{pmatrix} {\color{red}1} &{\color{red}-2} &{\color{red}4} \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1&{\color{red}0} \\ 5&{\color{red}3} \\ -1&{\color{red}0} \end{pmatrix}=\begin{pmatrix} a&{\color{red}b} \\ c&d \\ e &f \end{pmatrix}\rightarrow b=1\times 0+(-2)\times 3+4\times 0=-6 \nonumber \]

Para calcular\(c\), que es entrada (2,1), usamos la fila 2 de la matriz a la izquierda y la columna 1 de la matriz a la derecha:

\[\begin{pmatrix} 1&-2&4\\ {\color{red}5} &{\color{red}0} &{\color{red}3} \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} {\color{red}1} &0 \\ {\color{red}5} &3 \\ {\color{red}-1} &0 \end{pmatrix}=\begin{pmatrix} a&b \\ {\color{red}c}&d \\ e &f \end{pmatrix}\rightarrow c=5\times 1+0\times 5+3\times (-1)=2 \nonumber \]

Para calcular\(d\), que es entrada (2,2), usamos la fila 2 de la matriz a la izquierda y la columna 2 de la matriz a la derecha:

\[\begin{pmatrix} 1&-2&4\\ {\color{red}5} &{\color{red}0} &{\color{red}3} \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1&{\color{red}0} \\ 5&{\color{red}3} \\ -1&{\color{red}0} \end{pmatrix}=\begin{pmatrix} a&b \\ c&{\color{red}d} \\ e &f \end{pmatrix}\rightarrow d=5\times 0+0\times 3+3\times 0=0 \nonumber \]

Para calcular\(e\), que es entrada (3,1), usamos la fila 3 de la matriz a la izquierda y la columna 1 de la matriz a la derecha:

\[\begin{pmatrix} 1&-2&4\\ 5&0&3 \\ {\color{red}0} &{\color{red}1/2} &{\color{red}9} \end{pmatrix}\begin{pmatrix} {\color{red}1} &0 \\ {\color{red}5} &3 \\ {\color{red}-1} &0 \end{pmatrix}=\begin{pmatrix} a&b \\ c&d \\ {\color{red}e} &f \end{pmatrix}\rightarrow e=0\times 1+1/2\times 5+9\times (-1)=-13/2 \nonumber \]

Para calcular\(f\), que es entrada (3,2), usamos la fila 3 de la matriz a la izquierda y la columna 2 de la matriz a la derecha:

\[\begin{pmatrix} 1&-2&4\\ 5&0&3 \\ {\color{red}0} &{\color{red}1/2} &{\color{red}9} \end{pmatrix}\begin{pmatrix} 1&{\color{red}0} \\ 5&{\color{red}3} \\ -1&{\color{red}0} \end{pmatrix}=\begin{pmatrix} a&b \\ c&d \\ e&{\color{red}f} \end{pmatrix}\rightarrow f=0\times 0+1/2\times 3+9\times 0=3/2 \nonumber \]

El resultado es:

\[\displaystyle{\color{Maroon}\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1 &0 \\ 5 &3 \\ -1 &0 \end{pmatrix}=\begin{pmatrix} -13&-6 \\ 2&0 \\ -13/2 &3/2 \end{pmatrix}} \nonumber \]

Ejemplo\(\PageIndex{2}\)

Calcular

\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix}\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}\nonumber \]

Solución

Se nos pide multiplicar una\(2\times 3\) matriz por una\(3\times 1\) matriz (un vector de columna). El resultado será una\(2\times 1\) matriz (un vector).

\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix}\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}=\begin{pmatrix} a \\ b \end{pmatrix}\nonumber \]

\[a=1\times1+(-2)\times 5+ 4\times (-1)=-13\nonumber \]

\[b=5\times1+0\times 5+ 3\times (-1)=2\nonumber \]

La solución es:

\[\displaystyle{\color{Maroon}\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix}\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}=\begin{pmatrix} -13 \\ 2 \end{pmatrix}}\nonumber \]

¿Necesitas ayuda? El siguiente enlace contiene ejemplos resueltos: Multiplicando matrices de diferentes formas (tres ejemplos): http://tinyurl.com/kn8ysqq

Enlaces externos:

• Multiplicando matrices, ejemplo 1: http://patrickjmt.com/matrices-multiplying-a-matrix-by-another-matrix/
• Multiplicando matrices, ejemplo 2: http://patrickjmt.com/multiplying-matrices-example-2/
• Multiplicando matrices, ejemplo 3: http://patrickjmt.com/multiplying-matrices-example-3/

El Conmutador

La multiplicación matricial no es, en general, conmutativa. Por ejemplo, podemos realizar

\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix}\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}=\begin{pmatrix} -13 \\ 2 \end{pmatrix} \nonumber \]

pero no puede realizar

\[\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix} \nonumber \]

Incluso con matrices cuadradas, que se pueden multiplicar en ambos sentidos, la multiplicación no es conmutativa. En este caso, es útil definir el conmutador, definido como:

\[[\mathbf{A},\mathbf{B}]=\mathbf{A}\mathbf{B}-\mathbf{B}\mathbf{A} \nonumber \]

Ejemplo\(\PageIndex{3}\)

Dado\(\mathbf{A}=\begin{pmatrix} 3&1 \\ 2&0 \end{pmatrix}\) y\(\mathbf{B}=\begin{pmatrix} 1&0 \\ -1&2 \end{pmatrix}\)

Calcular el conmutador\([\mathbf{A},\mathbf{B}]\)

Solución

\[[\mathbf{A},\mathbf{B}]=\mathbf{A}\mathbf{B}-\mathbf{B}\mathbf{A}\nonumber \]

\[\mathbf{A}\mathbf{B}=\begin{pmatrix} 3&1 \\ 2&0 \end{pmatrix}\begin{pmatrix} 1&0 \\ -1&2 \end{pmatrix}=\begin{pmatrix} 3\times 1+1\times (-1)&3\times 0 +1\times 2 \\ 2\times 1+0\times (-1)&2\times 0+ 0\times 2 \end{pmatrix}=\begin{pmatrix} 2&2 \\ 2&0 \end{pmatrix}\nonumber \]

\[\mathbf{B}\mathbf{A}=\begin{pmatrix} 1&0 \\ -1&2 \end{pmatrix}\begin{pmatrix} 3&1 \\ 2&0 \end{pmatrix}=\begin{pmatrix} 1\times 3+0\times 2&1\times 1 +0\times 0 \\ -1\times 3+2\times 2&-1\times 1+2\times 0 \end{pmatrix}=\begin{pmatrix} 3&1 \\ 1&-1 \end{pmatrix}\nonumber \]

\[[\mathbf{A},\mathbf{B}]=\mathbf{A}\mathbf{B}-\mathbf{B}\mathbf{A}=\begin{pmatrix} 2&2 \\ 2&0 \end{pmatrix}-\begin{pmatrix} 3&1 \\ 1&-1 \end{pmatrix}=\begin{pmatrix} -1&1 \\ 1&1 \end{pmatrix}\nonumber \]

\[\displaystyle{\color{Maroon}[\mathbf{A},\mathbf{B}]=\begin{pmatrix} -1&1 \\ 1&1 \end{pmatrix}}\nonumber \]

Multiplicación de un vector por un escalar

La multiplicación de un vector\(\vec{v_1}\) por un escalar\(n\) produce otro vector de las mismas dimensiones que se encuentra en la misma dirección que\(\vec{v_1}\);

\[n\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} nx \\ ny \end{pmatrix} \nonumber \]

El escalar puede estirar o comprimir la longitud del vector, pero no puede girarlo (figure [fig:vector_by_scalar]).

Figura\(\PageIndex{2}\): Multiplicación de un vector por un escalar

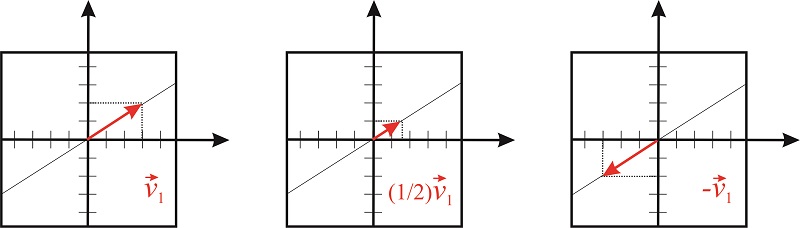
Multiplicación de una matriz cuadrada por un vector

La multiplicación de un vector\(\vec{v_1}\) por una matriz cuadrada produce otro vector de las mismas dimensiones de\(\vec{v_1}\). Por ejemplo, podemos multiplicar una\(2\times 2\) matriz y un vector bidimensional:

\[\begin{pmatrix} a&b \\ c&d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} ax+by \\ cx+dy \end{pmatrix} \nonumber \]

Por ejemplo, considere la matriz

\[\mathbf{A}=\begin{pmatrix} -2 &0 \\ 0 &1 \end{pmatrix} \nonumber \]

El producto

\[\begin{pmatrix} -2&0 \\ 0&1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \nonumber \]

es

\[\begin{pmatrix} -2x \\ y \end{pmatrix} \nonumber \]

Vemos que\(2\times 2\) las matrices actúan como operadores que transforman un vector bidimensional en otro vector bidimensional. Esta matriz particular mantiene el valor de\(y\) constante y multiplica el valor de\(x\) por -2 (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Multiplicación de un vector por una matriz cuadrada

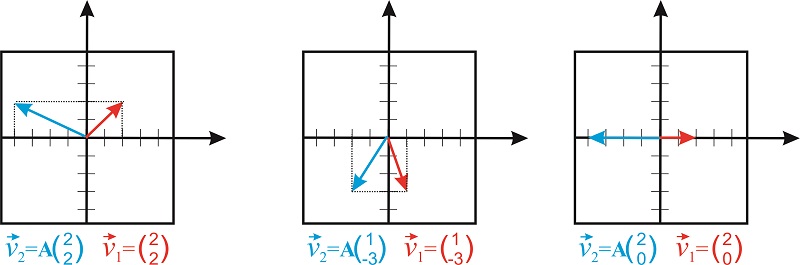
Observe que las matrices son formas útiles de representar operadores que cambian la orientación y el tamaño de un vector. Una clase importante de operadores que son de particular interés para los químicos son los llamados operadores de simetría.

Atribución

Esta página fue adaptada de Matrices (haga clic aquí), aportada por Marcia Levitus, Profesora Asociada (Instituto de Biodiseño) de la Universidad Estatal de Arizona.

Modified by Kathryn Haas (khaaslab.com)