1.2: El modelo cuánto-mecánico del átomo
- Page ID
- 70077
Dualismo de partículas de onda
El fenómeno del dualismo onda-partícula se descubrió por primera vez para la radiación electromagnética, y se extendió a todas las demás partículas, incluido el electrón. Se inició con la investigación del efecto fotoeléctrico de Albert Einstein (Fig. 1.2.1 y Fig. 1.2.2).

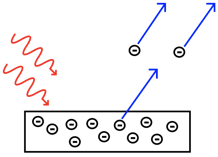
El efecto fotoeléctrico se produce cuando una superficie metálica es irradiada por la luz. Por encima de una cierta frecuencia, o por debajo de cierta longitud de onda, la luz es capaz de expulsar electrones de la superficie metálica. La frecuencia umbral depende del metal. Por debajo de la frecuencia umbral no se expulsan electrones. Einstein investigó la máxima energía cinética de los electrones expulsados en función de la frecuencia de la luz. Encontró que había una relación lineal. Analizó la pendiente de esta línea y encontró que la pendiente era la constante de Planck h, lo que significaría que los electrones tenían una energía E=h\(\nu\) menos una energía E B que sería necesaria para superar la energía de unión, también llamada función de trabajo, del electrón en el metal (Figura 1.2.3, izquierda).
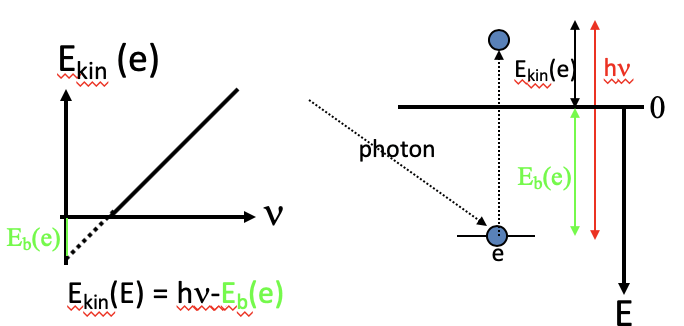
La ecuación E=h\(\nu\) fue derivada previamente por Planck (Fig. 1.2.4) con base en el supuesto de que la energía estaba cuantificada, y ahora Einstein la había encontrado experimentalmente nuevamente en la búsqueda de explicar el efecto fotoeléctrico. Esto significaría que se cuantificara la luz. La cuantificación se explicaría por el hecho de que la luz no solo tendría propiedades de onda sino también de partículas, y estas partículas se llamarían fotones. Suponiendo fotones el efecto fotoeléctrico podría explicarse fácilmente (Figura 1.2.3, derecha). Cuando la luz golpea la superficie metálica, el fotón choca con el electrón. Sólo cuando el fotón tuviera una energía mayor que la función de trabajo del metal, el electrón sería expulsado y tendría una energía cinética igual a la diferencia entre la energía del fotón y la energía de unión. El dualismo onda-partícula de la luz y la radiación electromagnética en general también se pueden derivar matemáticamente. Porque la masa se puede convertir en radiación electromagnética de acuerdo con la ecuación E = mc 2, y la energía de la radiación electromagnética es E=h\(\nu\), mc 2 =h\(\nu\). Podemos resolver la ecuación para\(\nu\), y luego es\(\nu\) =mc 2 /h. Con\(\nu\) =c/λ, y resuelta para λ, la ecuación se convierte en λ=h/mc. Esta ecuación muestra el dualismo de partículas de onda de la radiación electromagnética porque relaciona una longitud de onda con una masa. De hecho, la masa de la partícula asociada a la radiación electromagnética, el fotón, es inversa proporcional a la longitud de onda de la radiación electromagnética. El descubrimiento del dualismo onda-partícula de la radiación electromagnética fue un concepto radicalmente nuevo que es difícil de comprender intelectualmente hasta la fecha porque la mente humana tiende a ver ondas y partículas para ser mutuamente excluyentes. Sin embargo, es uno de los principios más fundamentales de la naturaleza. Como veremos más adelante, no sólo la radiación electromagnética muestra el dualismo de partículas de onda, sino todas las partículas incluyendo los electrones.

Dualismo de partículas onduladas de partículas masivas
Originalmente se pensó que el dualismo onda-partícula era válido solo para el fotón. Un joven estudiante francés de doctorado en física, Louis De Broglie tuvo la idea radical de que no solo el fotón, sino todas las partículas exhibirían el dualismo de partículas onduladas, incluido el electrón. La fórmula de Einstein λ = h/mc solo necesitaría ser reordenada ligeramente en λ = h/mv, donde m sería la masa de la partícula, y v sería la velocidad de la partícula. Esta idea fue muy disputada en su momento, y la tesis doctoral de Louis De Broglie casi no fue aceptada. Sin embargo, finalmente el dualismo onda-partícula del electrón fue probado por experimentos de difracción de electrones, y Louis De Broglie fue galardonado con el premio Nobel en 1929. Hoy, creemos que todas las partículas muestran el dualismo onda-partícula, y ningún experimento hasta la fecha indica una excepción.

Ondas Standing
Con el descubrimiento del dualismo onda-partícula del electrón, y la observación de la cuantificación de estados electrónicos en átomos, los físicos led se enfocan en un campo de la física en el que se cuantifican las ondas. El campo de ondas estacionarias (Fig. 1.2.6).
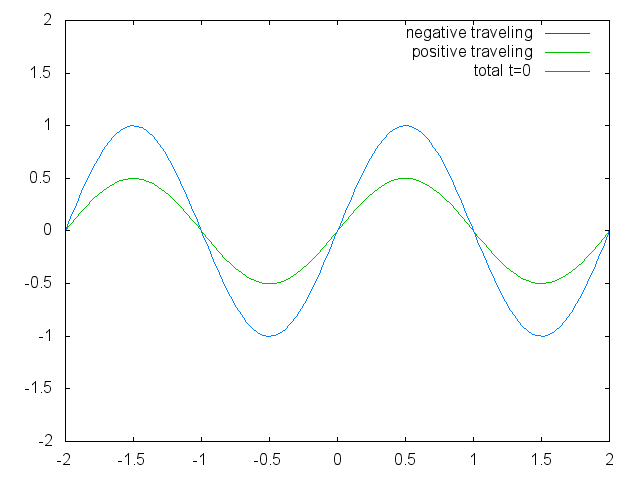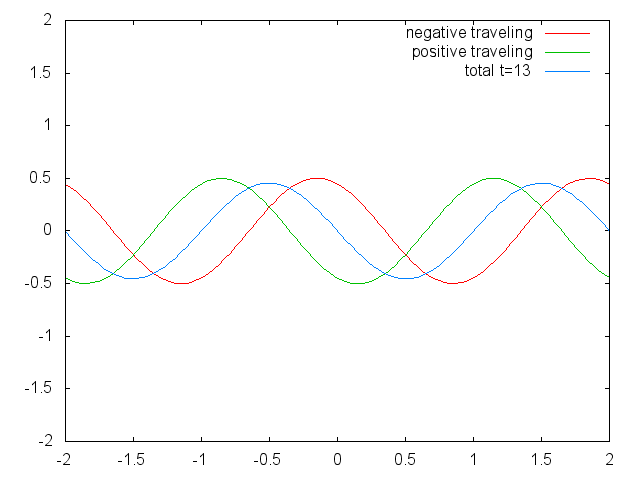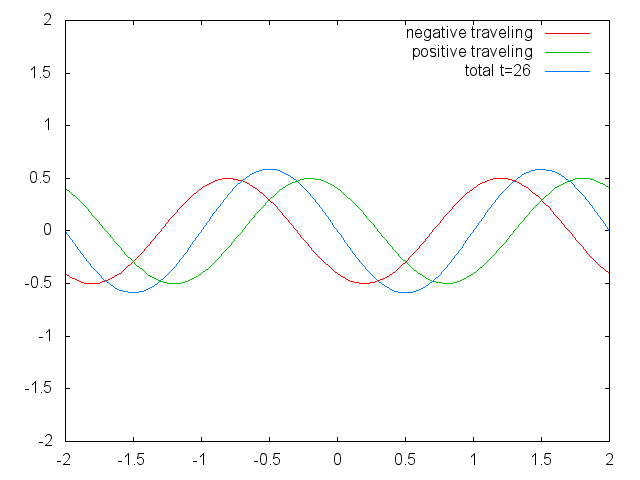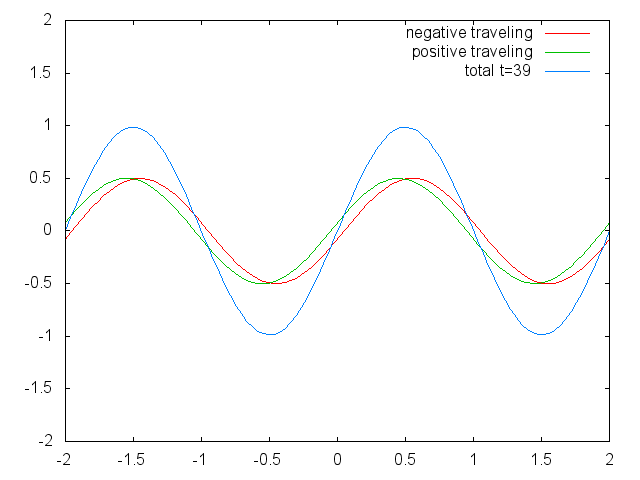
Figura 1.2.6 Dos ondas viajeras confinadas (rojas y verdes) que producen una onda estacionaria (azul) debido a su interferencia. (Atribución: Govindabalan [CC BY-SA (https://creativecommons.org/licenses/by-sa/3.0)], Commons.wikimedia.org/wiki/F... _animation.gif)
Las ondas estacionarias son un fenómeno bastante común. Por ejemplo, puedes activar ondas estacionarias arrancando una cuerda de guitarra. Esto hace que la cuerda de guitarra vibre en ondas estacionarias con longitudes de onda discretas y cuantificadas. La vibración con la longitud de onda más larga es la llamada vibración de tierra. Su longitud de onda es dos veces la longitud de la cuerda de guitarra. Además, son posibles los llamados armónicos superiores. El primer armónico tiene una longitud de onda igual a la longitud de la cuerda de guitarra, el segundo, tiene una longitud de onda igual a dos tercios de la longitud de la cuerda, el tercero tiene una longitud de onda igual a la mitad de la longitud de la cuerda, el cuarto tiene una longitud de onda igual a un tercio de la longitud de la guitarra cadena, y así cuarto (Fig. 1.2.7).
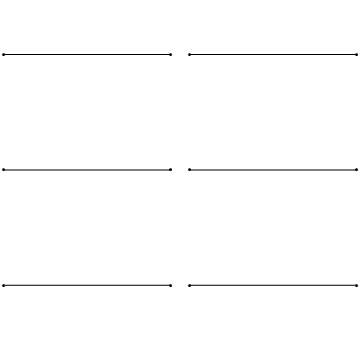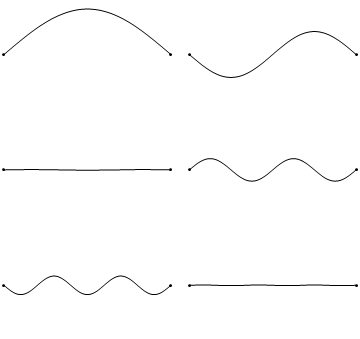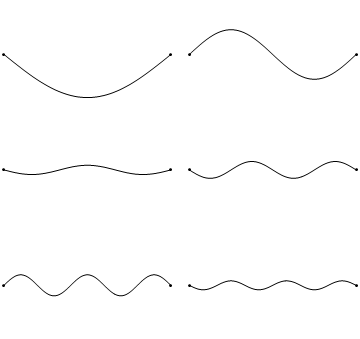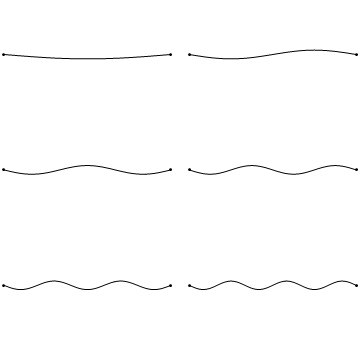
Se puede ver fácilmente que las posibles longitudes de onda a las que la cuerda puede vibrar siguen la ecuación λ=2L/N, donde n es un entero, o un número cuántico, y L es la longitud de la cuerda de guitarra. Así, podemos decir que se cuantifican las ondas asociadas a las vibraciones de la cuerda de guitarra. ¿Por qué estas olas se llaman ondas estacionarias? Esto se debe a que las posiciones de las crestas y los canales y los nodos no se mueven. Permanecen en la misma posición en la cuerda de guitarra en cualquier momento. Hay que decir aquí que la naturaleza permanente de las olas es en realidad una ilusión. En realidad hay dos ondas que viajan en dirección opuesta en la cuerda de guitarra, y estas ondas interfieren entre sí para que se produzca una onda estacionaria (esto se ilustra en la Fig. 1.2.6). Cuando se arranca la cuerda de guitarra, se envían dos ondas en dirección opuesta en la cuerda de guitarra hacia los dos extremos opuestos de la cuerda de guitarra. Una vez que han llegado a estos extremos son reflejados y enviados en sentido contrario hasta que vuelven a llegar a los extremos de la cuerda de guitarra donde vuelven a reflejarse. Durante este proceso, que ocurre una y otra vez, las dos ondas interfieren y producen la onda estacionaria. En suma, el hecho de que la onda esté confinada dentro de la cuerda de guitarra, conduce a las ondas estacionarias cuantificadas.
Electrón en una caja unidimensional
Háganos saber pasar de una cuerda de guitarra vibrante a un electrón en una caja unidimensional de longitud a que tiene paredes infinitamente altas. Dentro de la caja la energía potencial del electrón es cero, en las paredes la energía potencial es infinita (Figura 1.2.8).
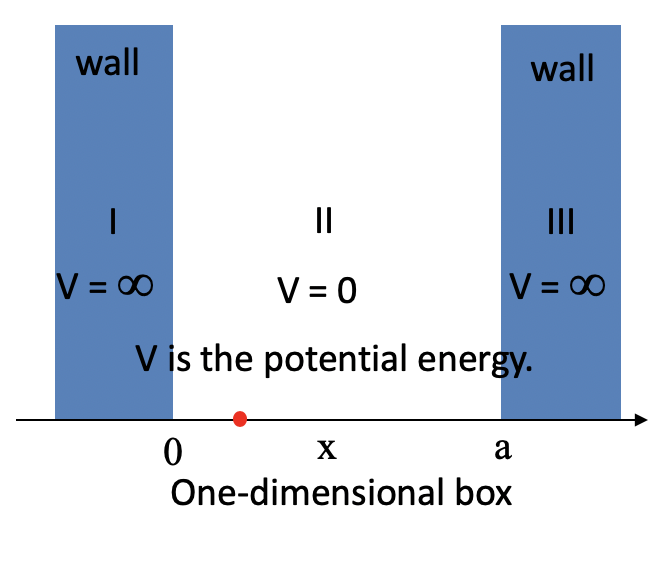
Debido a su energía cinética el electrón puede viajar en una línea dentro de la caja hasta que choca con la pared (Fig. 1.2.9, A). En la pared se está reflejando y obligando a viajar en sentido contrario hasta que de nuevo golpea la pared donde vuelve a invertir dirección, y así sucesivamente. Consideremos ahora que el electrón no sólo tiene partículas, sino también propiedades de onda. Por eso también una ola viaja a lo largo de la línea, se refleja en la pared, viaja en dirección opuesta, se refleja de nuevo y así sucesivamente. Estas ondas pueden interferir con ella otras al igual que las olas que viajan en la cuerda de la guitarra para producir una onda estacionaria. Así, el electrón en la caja unidimensional debe comportarse como una onda estacionaria, y esta onda debe ser cuantificada (Fig. 1.2.9, B-F).
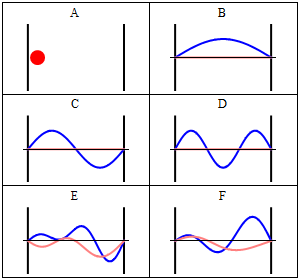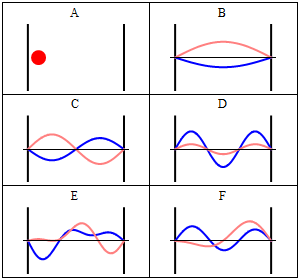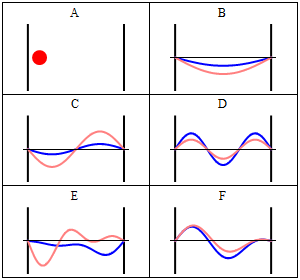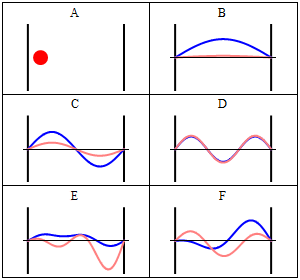
¿Cómo podemos describir matemáticamente el electrón en la caja como una onda estacionaria? Generalmente, se puede describir una onda estacionaria por una función de onda. Una función de onda indica la amplitud de la onda estacionaria en una posición particular en la caja unidimensional. ¿Cómo podemos encontrar la función de onda? Podemos partir de una ecuación diferencial que generalmente es válida para ondas estacionarias (Ec. 1.2.1).
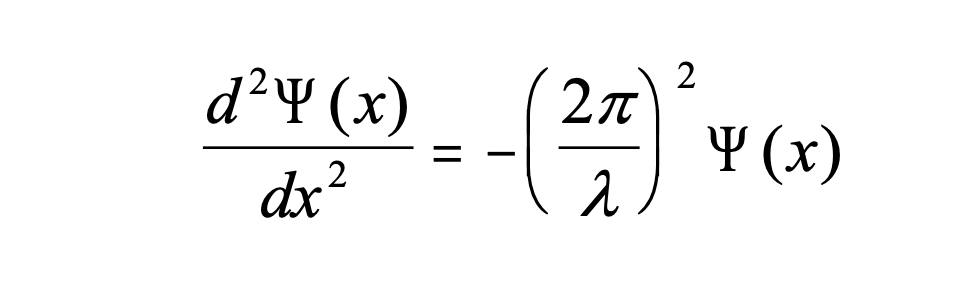
Ecuación 1.2.1 Ecuación diferencial de onda estacionaria.
Dice que la segunda derivada de la amplitud de la función de onda en la posición x es igual a — (2π/λ) 2 multiplicada por la amplitud de la función de onda en la posición x Consideremos ahora que la energía cinética del electrón es E = 1/2mv 2 y expandamos la ecuación por m.
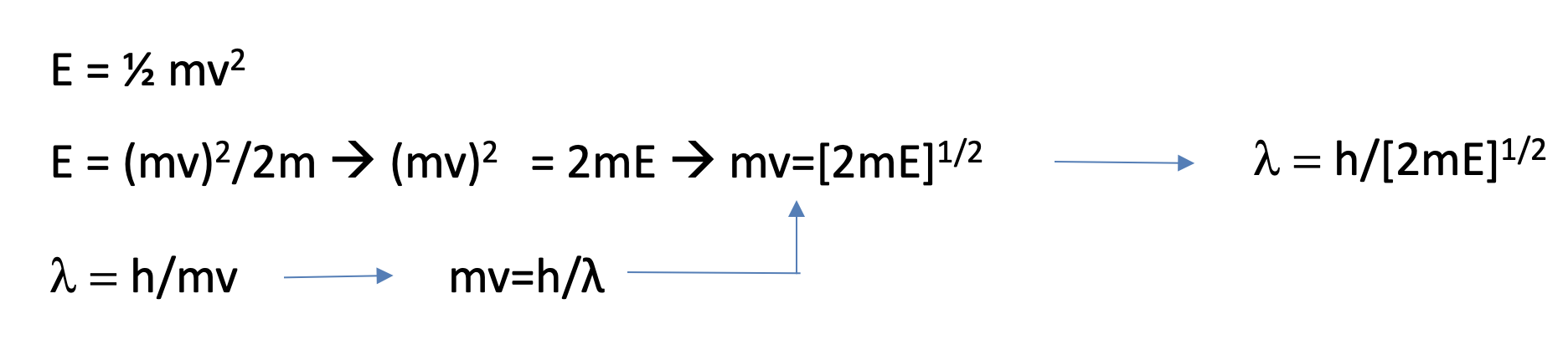
Ecuación 1.2.2 Resolución para λ a partir de la ecuación de energía cinética y la ecuación de De Broglie
Entonces resolvamos la ecuación para (mv). Ahora resolvamos la ecuación De Broglie para mv e insertemos mv por h/λ en la ecuación anterior. Finalmente, resolvamos la ecuación por λ y obtendremos λ = h/ [2Me] 1/2, Eq. 1.2.2. Ahora podemos sustituir λ por h/ [2Me] 1/2 en la ecuación diferencial. Ligeramente reordenada esta ecuación se convierte en la ecuación de Schrödinger para el electrón en el cuadro unidimensional (Ecuación 1.2.3).
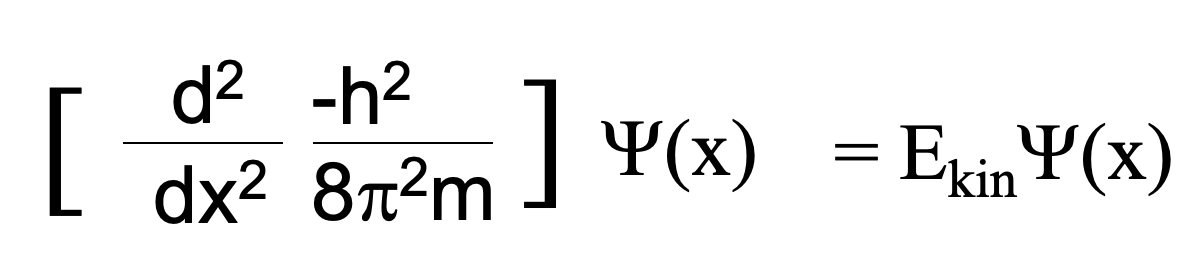
Ecuación 1.2.3 Ecuación de Schrödinger para el electrón en una caja 1-D.
La ecuación de Schrödinger es una ecuación diferencial. Para obtener la función de onda que describe el electrón en la caja necesitamos resolver la ecuación diferencial. Una posibilidad de resolver una ecuación diferencial es adivinar su solución, y después de eso demostrar que la solución es correcta. Este es el enfoque que queremos seguir aquí. Una función de onda muy general es aquella que es la suma de un término sinusal y un término cosinusal de la coordenada x por lo que asumiremos dos coeficientes generales r y s delante de x, y otros dos coeficientes generales A y B frente al seno y el término coseno, respectivamente.
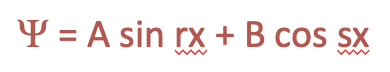
Ecuación 1.2.4 Solución genérica a la ecuación diferencial.
Ahora podemos pensar en las llamadas condiciones de límite para la función de onda que harán que la función de onda sea más específica. Una condición de límite es una propiedad que la función de onda debe tener para ser una solución sensible a la ecuación diferencial. Podemos asumir una primera condición de límite que asume que en la posición x=0 la amplitud de la función de onda debe ser 0. Esto se puede suponer porque en estas posiciones la “onda electrónica” se refleja en la pared. Eso significa que la función de onda no puede tener un término coseno y por lo tanto B debe ser 0. Si la función de onda tuviera un término coseno no sería 0 a x = 0 porque el coseno de 0 no es 0.
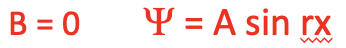
Ecuación 1.2.5 Condición de límite 1 para la función de onda
La segunda condición límite es que la amplitud de la función de onda es cero en x = a. Nuevamente, esto se debe a que el electrón golpea la pared en x = a e invierte su dirección. La función sinusal es solo cero en x = a cuando ra es un número entero n veces π: ra=nπ. Esto significa que r debe ser nπ/a.

Ecuación 1.2.6 Condición de límite 2 para la función de onda
Así, la función de onda debe ser A=Sin (nπx/a). Podemos ver que la función de onda que describe al electrón como una onda estacionaria en la caja unidimensional se cuantifica porque aparece el número cuántico n.

Ecuación 1.2.7 La función de onda considerando las condiciones de límite 1 y 2.
Insertar los números cuánticos n en las funciones de onda produce todas las ondas estacionarias que el electrón puede adoptar (Fig. 1.2.10). Se puede ver que el número de nodos y las longitudes de onda de las ondas dependen del número cuántico n. Para n = 0 no hay nodo y la longitud de onda es el doble de la longitud de la caja, para n = 2 hay un nodo y la longitud de onda es igual a la longitud de la caja, para n =3 hay tres nodos y la longitud de onda de la onda es 2/3 de las longitudes de la caja y así sucesivamente. Podemos ilustrar que la función de onda describe las ondas representadas en la Figura 1.2.10 con un ejemplo. La amplitud para la onda para n=2 es cero en el medio de la caja donde x = a/2. Si insertamos a/2 en la ecuación para ψ entonces ψ = A sin (nπ2a/a) = A sin (nπ) = 0 porque es la propiedad de una función sinusal ser 0 en un número entero múltiplo de π. También podríamos insertar otros valores para x y n en la función de onda, y obtendríamos la amplitud esperada. Esto demuestra que la función de onda representa correctamente las ondas estacionarias que el electrón puede adoptar.
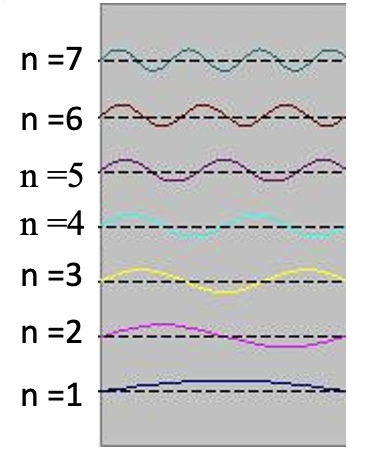
Todavía no hemos terminado del todo con la función de onda porque no hemos determinado el parámetro A frente al término sinusal. Para obtenerlo necesitamos considerar una tercera condición de límite (Ec. 1.2.8).
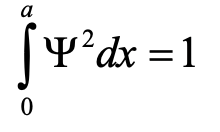
Ecuación 1.2.8 Condición de límite 3.
Dice que la integral del cuadrado de la función de onda sobre la longitud de la caja debe ser igual a uno. Podemos entender esta condición límite cuando consideramos que el cuadrado de la función de onda representa la probabilidad de encontrar el electrón en una posición particular en la caja. El valor que adopta el cuadrado de ψ en una posición x dentro de la caja representa la probabilidad de encontrar el electrón en esta posición cuando consideramos el electrón como una partícula. A esto se le llama la interpretación Born de la función de onda, que lleva el nombre del físico alemán Max Born.
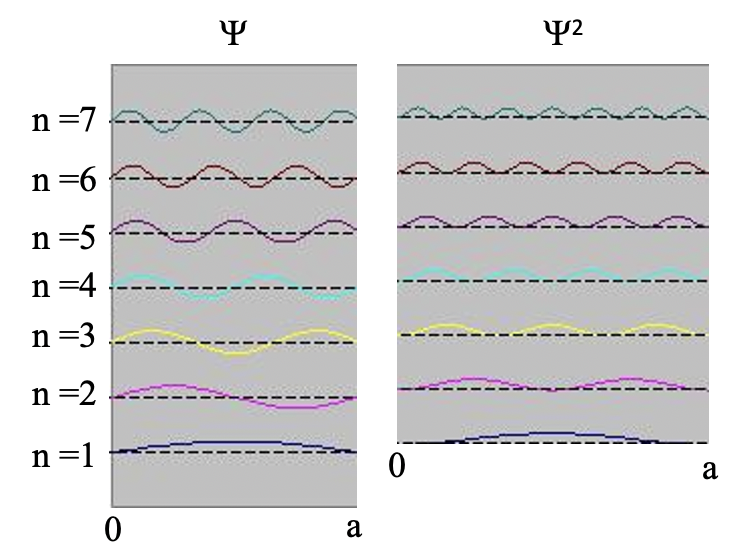
Debido a que la probabilidad de encontrar el electrón en cualquier parte de la caja debe ser del 100%, la integral del cuadrado de la función de onda sobre toda la caja debe ser del 100% o 1. Se puede mostrar, y omitimos los pasos matemáticos necesarios para mayor claridad aquí, que la condición de límite solo se cumple cuando A es igual a la raíz cuadrada de 2/a. la función de onda final es entonces psi es igual a 2/a sin (nπx/a). El factor raíz cuadrada de 2/a se llama la constante de normalización de la función de onda porque ajusta la amplitud de la función de onda para que la probabilidad de encontrar el electrón en cualquier lugar de la caja sea del 100%.
La ecuación de Schrödinger para el átomo H
Pasemos ahora de un electrón en una caja unidimensional al electrón en el átomo de hidrógeno. Lo que es similar y lo que es diferente entre estos dos casos. Una similitud es que el electrón está confinado en un átomo al igual que el electrón está confinado en la caja 1D. Así, como en la caja unidimensional el electrón debería comportarse como una onda estacionaria. Mientras que en el cuadro unidimensional solo hay una coordenada a considerar, hay tres coordenadas a considerar para el electrón en el átomo. Esto se debe a que un átomo es esférico y por lo tanto son necesarias tres coordenadas x, y y z para describir una posición dentro del átomo. Una segunda diferencia importante es que la energía potencial del electrón es cero en cualquier posición dentro de la caja, mientras que no es cero en el átomo de hidrógeno. Esto se debe a que en un átomo hay atractivas fuerzas de Coulomb entre el núcleo y el electrón. Cuanto más lejos esté el electrón del núcleo, mayor será su energía potencial. Esto se debe a que se necesita energía para sacar el electrón del núcleo.

Por lo tanto, necesitamos modificar la ecuación de Schrödinger que usamos anteriormente para el cuadro unidimensional de la siguiente manera. En primer lugar, necesitamos expandir el operador para la energía cinética de una a tres dimensiones e introducir las coordenadas y y z además de x; en segundo lugar, tenemos que agregar un operador para la energía potencial a la ecuación. La energía potencial es la energía de Coulomb entre el protón y el electrón. Es similar al término que usamos anteriormente para el cálculo de la energía potencial del electrón en el modelo de Bohr. En lugar del radio r usamos ahora la raíz cuadrada de la suma del cuadrado de las tres coordenadas x, y y z, para indicar la energía Coulomb del electrón en cualquier posición dentro del átomo. Nuestra función de onda ahora será una función de tres coordenadas x, y y z, lo que significa que nuestra función de onda ahora será tridimensional y representará ondas estacionarias tridimensionales. Las ondas tridimensionales son más difíciles de imaginar en comparación con las unidimensionales, pero tienen las mismas propiedades, que son que la posición de las crestas, depresiones y nodos no se mueve.
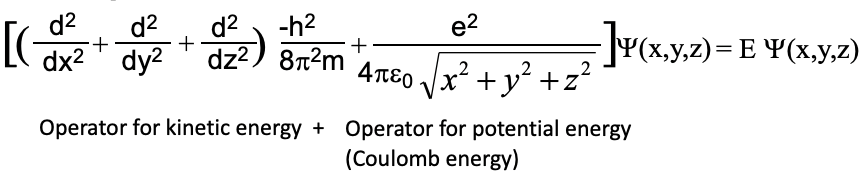
Ecuación 1.2.9 Ecuación de Schrödinger para el átomo H.
Para obtener las funciones de onda para el electrón necesitamos resolver la ecuación de Schrödinger para el átomo de hidrógeno. Para ello, necesitamos pensar en las condiciones de límite para la función de onda. Una condición es que el cuadrado de la función de onda se acerca a cero cuando vamos muy lejos del núcleo, y r, la distancia desde el núcleo se acerca a infinito. En segundo lugar, como en la caja unidimensional, la función integral sobre el cuadrado de la onda debe ser una. Esto se debe a que la probabilidad de encontrar el electrón en algún lugar del átomo debe ser del 100%. En tercer lugar, sería sensato suponer que la función de onda debe ser continuamente diferenciable y de valor único (Fig. 1.2.13).

El sistema de coordenadas polares esféricas
El proceso matemático para resolver la ecuación de Schrödinger está más allá del alcance de este curso y se le remite a clases de Química Física y libros de texto para los detalles. Aquí solo proporcionaremos un breve resumen del proceso. Es matemáticamente más sencillo resolver la ecuación de Schrödinger en coordenadas polares esféricas en lugar de coordenadas cartesianas. Por lo tanto, obtenemos las soluciones de la ecuación de Schrödinger, las funciones de onda, en coordenadas polares. La posición de un punto se especifica con tres números: la distancia radial de ese punto desde un origen fijo, su ángulo polar medido desde una dirección cenital fija, y el ángulo azimutal de su proyección ortogonal sobre un plano de referencia que pasa por el origen y es ortogonal al cenit, medido desde una dirección de referencia fija en ese plano (Fig. 1.2.14).
Soluciones de la Ecuación de Schrödinger
La función de onda es entonces una función de r, θ y φ, en particular es un producto de una función de onda radial que es función de r, una función de onda de colatitud, que es una función de θ, y una función de onda acimutal que es una función de φ (Ec. 1.2.10). Se pueden ver las formas explícitas de las funciones radial, colatitud y acimutal en la Fig. 1.2.15.
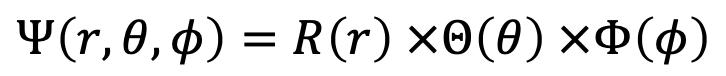
Ecuación 1.2.10 La función de onda para el electrón en el átomo de H como una función de r, θ y φ
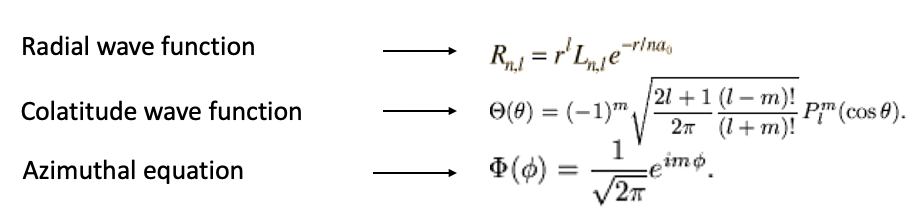
No necesitamos entender todos los detalles aquí, pero necesitamos darnos cuenta de que estas funciones de onda son funciones de los números cuánticos. En contraste con el electrón en la caja unidimensional no solo es necesario considerar uno, sino tres números cuánticos. Más allá del número cuántico n, que es el llamado número cuántico principal, también hay un llamado número cuántico orbital l, y un número cuántico magnético m. El número cuántico n solo ocurre en la función de onda radial, el número cuántico l solo ocurre en la función radial y de colatitud, y la cuántica número m sólo ocurre en la colatitud y la parte acimutal de la función de onda. Los valores que el número cuántico orbital l puede adoptar dependen de n, puede estar entre 0 y n-1 para un número cuántico dado n. El número cuántico magnético m depende del número cuántico l, y puede ir de —l a +l. Entonces, por ejemplo, cuando n es igual a 2, l puede variar entre 0 y 1, y para l igual a 2, m puede adoptar cualquier valor entre -2 y 2, es decir -2, -1, 0, +1 y +2 (Fig. 1.2.16).

Estas funciones de onda tienen un nombre particular en química. Se les llama orbitales. Uno puede entender un orbital como la función de onda tridimensional que describe el electrón en un átomo como una onda estacionaria. Así, un orbital es un estado que el electrón puede adoptar, y cuando decimos que un electrón está en un orbital particular nos referimos a que el electrón está en un estado particular.
El número cuántico de giro s
Dentro de un orbital, un electrón puede adoptar dos espines diferentes descritos por el número cuántico de espín s. Este número cuántico no es resultado de la ecuación de Schrödinger, sino que se encontró experimentalmente. El número cuántico de espín s puede adoptar dos valores: +1/2 y -1/2. Decimos que un electrón es spin up cuando s = +1/2, y spin down cuando s = -1/2.
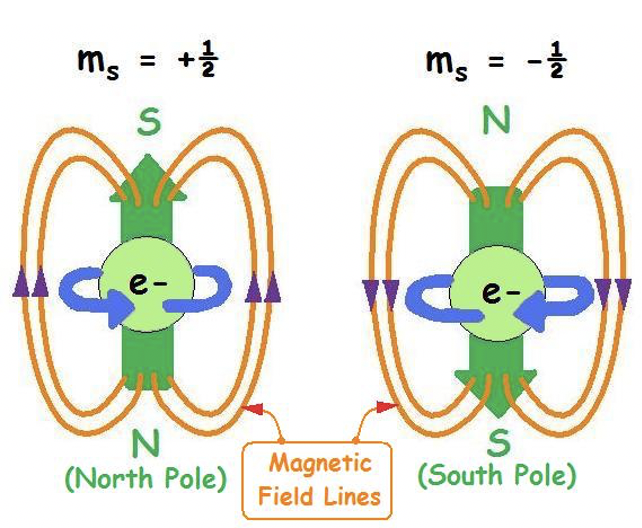
chem.libretexts.org/ @api /dek...jpg? revisión=1, CC BY-NC-SA 3.0)
El número cuántico de espín se entiende más fácilmente cuando se ve el electrón como una partícula que gira alrededor de su propio eje. Una rotación en sentido antihorario estaría asociada con s=+1/2, una rotación en sentido horario estaría asociada con s=-1/2. La rotación produce un campo magnético con la dirección de las líneas de campo dependiendo de la dirección de rotación.
El orbital 1s
Ahora insertemos los números cuánticos en la forma general de la función de onda para el electrón en el átomo de hidrógeno, y calculemos sus formas matemáticas explícitas. Empecemos con los números más pequeños posibles. Cuando insertamos n=1, l=0 y m=0 obtenemos la función de onda para el orbital 1s (Eq. 1.2.11).
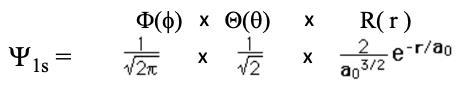
Ecuación 1.2.11 Función de onda para el orbital 1s
Se puede ver que la colatitud y las partes acimutales de las funciones de onda, juntas también llamadas parte angular de la función de onda, son números simples, es decir, uno sobre la raíz cuadrada de dos pi, y uno sobre la raíz cuadrada de dos respectivamente. Los ángulos theta y phi no aparecen y eso significa que la función de onda es independiente del ángulo. Esto implica que el orbital tiene una forma esférica.

La parte radial de la función de onda tiene un término exponencial e a la potencia de —r sobre un 0. El número e es el número de Euler, es decir, la base del logaritmo natural. Es aproximadamente igual a 2.71828. a 0 es el radio de Bohr, que es la distancia del electrón desde el protón para el electrón en su primera órbita según el modelo de átomos de Bohr. Lo calculamos previamente, y fue de 5.29 x 10 -11 m. r es la distancia desde el núcleo. Este término exponencial tiene una constante delante de él que es 1 sobre el radio de Bohr a la potencia de tres sobre dos. Debido a que la parte radial de la función de onda es e a la potencia de —r, la amplitud de la parte radial de la función de onda disminuye exponencialmente al aumentar la distancia r desde el núcleo. Esto es cierto para toda la función de onda porque las partes angulares de la función de onda son solo números simples. Se puede ver la disminución exponencial de la amplitud de la función de onda en función del radio r en unidades del radio de Bohr a 0 en la gráfica siguiente (Fig. 1.2.19).
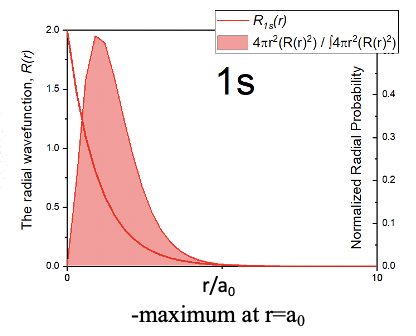
Esto significa que el orbital 1s debe ser un orbital esférico con su amplitud disminuyendo exponencialmente al aumentar la distancia desde el núcleo. Esto se puede representar gráficamente a través de una densidad de puntos alrededor del núcleo (Fig. 1.2.18). Una mayor densidad de puntos significa mayor amplitud y una menor densidad de puntos significa menor amplitud. El hecho de que la amplitud sea la más alta más cercana al núcleo significa que la probabilidad de encontrar el electrón en un punto particular en el espacio es la más alta más cercana al núcleo. Esto se debe a que el cuadrado de la función de onda para el orbital 1s representa la probabilidad de encontrar el electrón en un punto particular en el espacio. Sin embargo, la probabilidad de encontrar el electrón a cierta distancia del núcleo no es la más alta más cercana al núcleo. Esto se debe a que la probabilidad de encontrar el electrón a cierta distancia del núcleo es la probabilidad de encontrar el electrón en un punto particular en el espacio multiplicado por el número de puntos en el espacio que tienen esa distancia particular. El número de puntos en el espacio que tienen una distancia particular r del núcleo está relacionado con la superficie de una esfera con el radio a r. La superficie de una esfera A viene dada por la fórmula A=4πR 2. Así, la probabilidad de encontrar el electrón a una distancia particular r del núcleo es igual a la superficie de una esfera con el radio r veces la función de onda radial cuadrada. Esto define la función de probabilidad radial R P = 4πr 2 R2.
La gráfica para la función de probabilidad radial se representa en la Figura 1.2.19. Se puede ver que es cero cuando r=0 que se debe al término r 2 que se convierte en cero a r = 0. A valores pequeños r el término 4πr 2 domina la función general y la probabilidad de encontrar el electrón aumenta con r Sin embargo, debido a que el término exponencial de la función radial se vuelve cada vez más significativo a valores r mayores, la función de probabilidad radial pasa por un máximo y luego declina. A distancias r acercándose al infinito la función se acerca a cero. El máximo de la curva representa la distancia a la que es más probable que encuentre el electrón. Curiosamente, es igual al radio de Bohr r. Eso significa que Bohr no estaba tan equivocado después de todo. No obstante, se equivocó en el sentido de que veía al electrón como una partícula clásica estando solo en ese radio. En cambio, el electrón, debido a sus propiedades de onda, no sólo se encuentra en el radio de Bohr r 0, sino que lo más probable es que lo podamos encontrar ahí.
El resultado de que la probabilidad de encontrar el electrón en un punto específico en el espacio es la mayor en el núcleo elimina la cuestión de por qué el átomo H no colapsa. Debido a que la amplitud de la función de onda es la más cercana al núcleo podemos decir realmente de una manera que el átomo está colapsado. Sin embargo, el átomo es principalmente espacio vacío debido a la deslocalización de la función de onda que describe el estado del electrón. La deslocalización del electrón debido a sus propiedades de onda también hace que la cuestión del tamaño de un orbital no sea trivial. La función de onda se acerca a cero solo para r acercándose al infinito, pero nunca se vuelve cero. Esto significa que para dar cuenta de toda la densidad de electrones el orbital sería infinitamente grande. Sin embargo, esta no sería una definición sensata. La definición comúnmente aceptada es que el tamaño de un orbital está definido por el espacio que contiene el 90% de su densidad electrónica. Podemos representar orbitales de acuerdo con esta definición. Para el caso del orbital 1s se elige el radio de la esfera que representa el orbital 1s de manera que la probabilidad de encontrar el electrón dentro de una esfera de ese radio sea del 90%.
El orbital 2s
Insertar n=2, l=0 y m=0 en la función de onda general nos da la función de onda para el orbital 2s (Ec. 1.2.12).
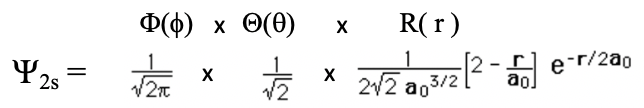
Ecuación 1.2.12 Función de onda para el orbital 2s
Al igual que en el caso del orbital 1s, las partes angulares de la función de onda son solo números simples. Así, el orbital 2s es también un orbital esférico. Al igual que en el orbital 1s, la parte radial de la función de onda tiene un término exponencial del tipo e-r y un coeficiente simple. No obstante, existe un término adicional 2-r/a 0. Debido al término exponencial, la amplitud de la función de onda disminuye exponencialmente con r. Sin embargo, debido al término 2-r/a 0 la función de onda se vuelve negativa, y luego se acerca a 0. El radio en el que la función de onda cambia su signo algebraico se denomina nodo esférico. El nodo es esférico porque describe que la superficie es una esfera. En la superficie de esta esfera la amplitud de la función de onda es cero. El radio en el que la función de onda cambia su signo algebraico es 2a 0. Esto queda claro cuando consideramos que el término 2-r/a 0 se convierte en cero cuando r=2a 0 porque 2-2a 0 /a 0 =0. Cuando este término es cero entonces toda la función de onda se convierte en cero. Podemos ilustrar el cambio del signo algebraico en el orbital 2s usando colores como se muestra a continuación (Fig. 1.2.20).
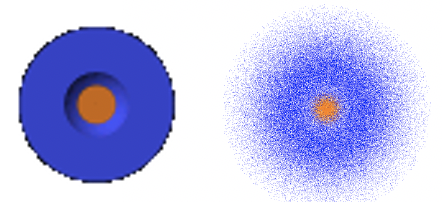
La esfera naranja indica el espacio en el que la amplitud del orbital 2s es positiva, y el área azul indica dónde es negativa. El área de interfaz donde cambia el color representa el nodo. Al multiplicar el cuadrado de la función de onda radial R por 4πr 2 obtenemos la función de probabilidad radial para el orbital 2s (Fig. 1.2.21).
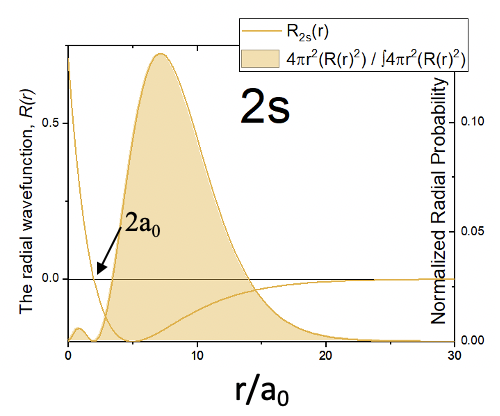
Se puede ver que similar al orbital 1s, la probabilidad de encontrar el electrón en un radio más cercano al núcleo es 0. Sin embargo, a diferencia del orbital 1s, ahora hay dos máximos en lugar de solo uno. Este segundo máximo es impuesto por el nodo esférico del orbital 2s. El segundo máximo es mayor que el primero. Generalmente, la probabilidad de encontrar el electrón más lejos del núcleo es mayor en comparación con el orbital 1s. Eso significa que el orbital 2s es más grande que el orbital 1s. Esto refleja la tendencia general de que los orbitales con un número cuántico mayor n tienden a ser mayores y la probabilidad de encontrar el electrón más lejos del núcleo es mayor.
El Orbital de los 3
Veamos una s orbital más, la orbital 3s (Eq. 1.2.13).
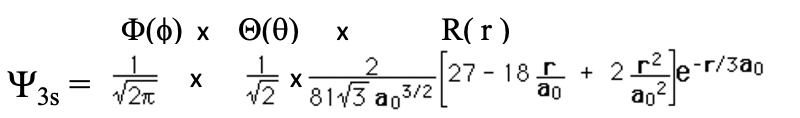
Ecuación 1.2.13 Función de onda para el orbital 3s.
Las partes angulares de la función de onda para el orbital 3s son nuevamente números simples, lo que implica que el orbital vuelve a ser esférico. Generalmente todos los orbitales son esféricos.
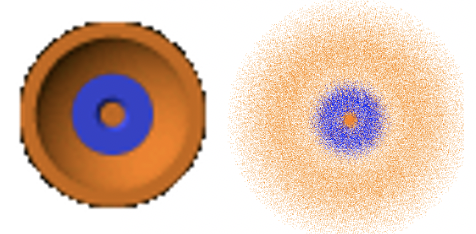
La parte radial de la función de onda se puede dividir en las partes. La primera parte es un número simple, luego está el término 27-18r/a 0 + 2r 2 /a 0 2, y el término exponencial e -r/3a 0. Debido a la parte exponencial la amplitud de la función de onda disminuye exponencialmente al aumentar r. Sin embargo, entonces la función de onda se vuelve negativa, pasa por un mínimo, luego vuelve a ser positiva, pasa por un pequeño máximo, y finalmente se acerca a cero. El hecho de que la función de onda cambie su signo algebraico dos veces significa que el orbital 3s tiene dos nodos esféricos. Estos nodos esféricos se deben al segundo término que es una función cuadrada del tipo ax 2 + bx + c, por lo que en este caso a = 2/a 0 2, b =-18/a 0 y c=27. Cuando este término se convierte en cero, toda la función de onda se convierte en cero. Las funciones cuadradas tienen dos soluciones de acuerdo con la fórmula x= (-b±√ (b 2 -4ac)) /2a. Las soluciones dan los radios para los dos nodos esféricos de la órbita 3s. Aquí omitimos el cálculo exacto de los radios por razones de breveza y claridad. Puedes calcularlos como tarea.
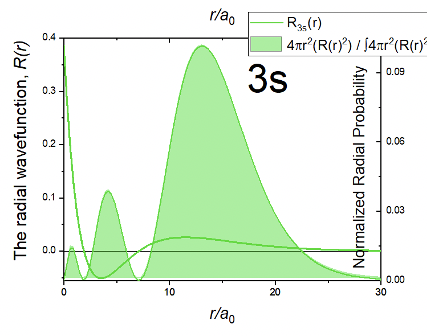
Debido a los dos nodos esféricos, la función de probabilidad radial R p tiene tres máximos. Uno muy pequeño cercano al núcleo, son más grandes uno más lejos del núcleo, y el más grande a una distancia aún mayor del núcleo. En general, el orbital 3s es mayor que el orbital 2s, lo que confirma la tendencia general de que los orbitales aumentan de tamaño al aumentar el número cuántico n.
El Orbital 2p z
Ahora veamos los orbitales en los que el número cuántico orbital l es mayor que 0. Cuando l es igual a 1, entonces n debe ser al menos 2. Un orbital con n=2 y l=1 es un orbital 2p. En general, deben existir tres orbitales 2p porque para l=1, el número cuántico magnético m puede adoptar tres valores: -1, 0 y +1. El orbital con m=0 se llama orbital 2p z. Veamos la forma matemática de esta función de onda (Eq. 1.2.14).
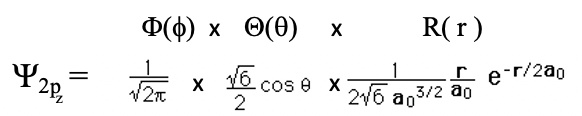
Ecuación 1.2.14 Función de onda para el orbital 2p z
Analizar las partes angulares de la función de onda muestra que si bien la parte acimutal sigue siendo un número simple, la parte de colatitud no lo es, es una función de θ. Esto significa que la amplitud de la función de onda ahora depende del ángulo, lo que implica que el orbital no puede ser esférico. En cambio, el orbital 2p tiene la forma de una mancuerna que está orientada a lo largo del eje z. Un lóbulo está por encima del plano xy, y el otro lóbulo está por debajo del plano xy. Estos dos lóbulos diferentes tienen un signo algebraico diferente, indicado por diferentes colores (Fig. 1.2.24).
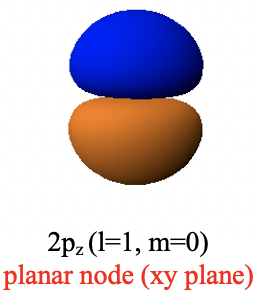
Dentro del plano xy la amplitud de la función de onda es cero. El plano xy representa un denominado nodo plano. Un nodo plano es un tipo de nodo angular. El nombre nodo angular se debe a que se debe a que la parte angular de la función de onda no es un simple número, sino una función de un ángulo, en este caso θ. Podemos mostrar que la parte angular de la función de onda produce el nodo plano en el plano xy cuando lo convertimos de coordenadas esféricas a cartesianas (Eq. 1.2.15).
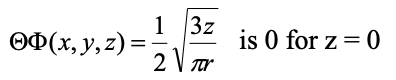
Ecuación 1.2.15 Parte angular de la función de onda de 2p z en coordenadas cartesianas. La función se convierte en cero cuando z=0.
Podemos ver que la parte angular de la función de onda es sólo una función de z. También podemos ver, que la parte angular de la función de onda se vuelve cero cuando z=0. Cuando la parte angular de la función de onda se convierte en cero, entonces la función de onda de todo el orbital se vuelve cero. Z es cero solo en el plano xy, y esto explica por qué el plano xy es un nodo plano.
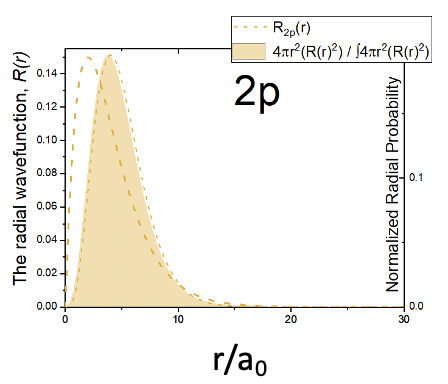
Ahora veamos la parte radial de la función de onda. Se compone de tres términos: una constante simple, el término r/a 0, y el término exponencial e -r/2a 0. Debido al término r/a 0 la parte radial de la función de onda es cero en r=0. Esto significa que es muy poco probable encontrar el electrón en un punto en el espacio directamente en el núcleo. Este comportamiento es opuesto a los orbitales s. Debido a que el término r/a 0 domina el comportamiento de la función de onda a un valor r pequeño, la amplitud primero aumenta. Sin embargo, a valores r mayores el término exponencial se vuelve más importante lo que fuerza la amplitud de la función radial a través de un máximo, después de lo cual disminuye y se acerca a cero. La función de onda radial nunca cambia el signo algebraico. Por lo tanto, el orbital 2p z no tiene un nodo esférico. La función de probabilidad radial tiene una forma similar en comparación con la función radial. Es cero en r=0 y pasa por un máximo antes de que disminuya de nuevo y se acerque a cero (Figura 1.2.25).
El Orbital 2p x y 2p y
Los orbitales 2p x y 2p y se obtienen cuando los números cuánticos m son 1 y -1, respectivamente.
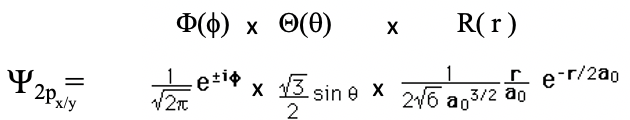
Ecuación 1.2.16 Función de onda para las orbitales 2p x y 2p y
Tienen la misma forma que el orbital 2p z, pero su orientación es diferente. La mancuerna de la órbita 2p x está orientada a lo largo del eje x, y la del orbital 2p y está orientada a lo largo del eje y.
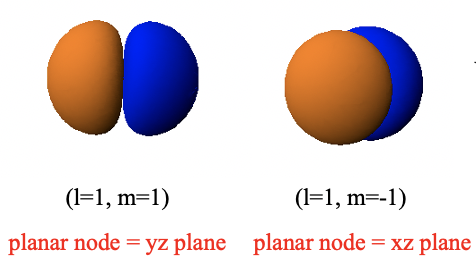
Esto se debe a que el orbital 2p x tiene un nodo plano en el plano yz, y el orbital 2p y tiene un nodo plano en el plano xz. Los nodos planos se deben a la parte angular de las funciones de onda de estos orbitales.
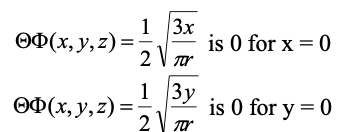
Ecuación 1.2.17 Parte angular de la función de onda de 2p x y 2p y, respectivamente. Las funciones de onda se convierten en 0 para x=0 e y=0, respectivamente.
Como se puede ver, las partes angulares de la función de onda contienen tanto los ángulos θ como Φ. Cuando se convierte en coordenadas cartesianas (Ec. 1.2.17) se puede ver que la función angular del orbital 2p x es solo una función de x, y la función angular del orbital 2p y es solo una función de y. Las funciones se convierten en cero para x=0 e y=0, respectivamente. X es cero solo en el plano yz, e y es cero solo en el plano xz, de ahí que estos nodos sean nodos planos. La función de onda radial es exactamente la misma que para el orbital 2p z.
Los orbitales 3p
Ahora veamos los orbitales 3p. En un orbital de 3p el número cuántico n=2 y l=1. Al igual que para el caso de los orbitales 2p hay tres orbitales p porque el número cuántico magnético m puede adoptar los valores -1, 0 y +1. A continuación se muestra la función de onda del orbital 3p z (Ec. 1.2.18).
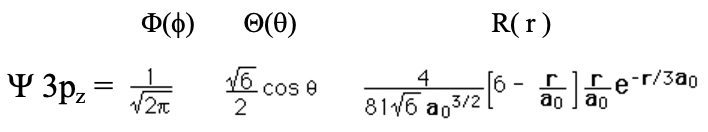
Ecuación 1.2.18 Función de onda para el orbital 3p z
Se puede ver que la parte angular de la función de onda es exactamente la misma que para el orbital 2p z. Esto significa que al igual que en el orbital 2p z debe haber un nodo plano en el plano xy. Cuando miras la parte radial de la función de onda puedes ver que está compuesta por cuatro términos, una constante simple, un término 6-r/a 0, el término r/a 0, y el término exponencial e -r/3a 0. Debido al término r/a 0 la función de onda se convierte en cero a r=0. Debido al término 6-r/a 0 la función de onda tiene un nodo esférico. Esto se debe a que cuando 6-r/a 0 =0 la función de onda completa se convierte en 0. Podemos determinar el radio en el que la función de onda se convierte en cero resolviendo la ecuación 6-r/a 0 =0 para r, que da r=6a 0. En general, la función radial es cero en r=0, pasa por un máximo, cambia su signo algebraico en el nodo esférico en r=6a 0, tiene un mínimo, y luego se acerca a cero para distancias muy grandes r (Fig. 1.2.28).
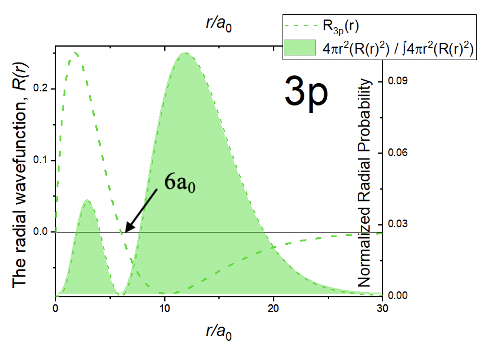
La función de probabilidad radial tiene dos máximos, uno pequeño cerca del núcleo y otro más grande más alejado del núcleo. En general, la función de probabilidad radial está más alejada del núcleo en comparación con los orbitales 2p, lo que implica que el orbital 3p es mayor.
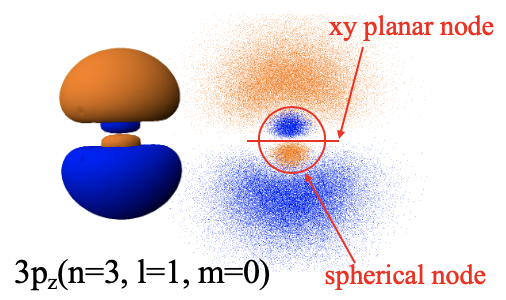
La forma general de la órbita 3p z está determinada por el nodo esférico y plano (Fig.1.2.29). Debido al nodo plano en el plano xy tiene forma de mancuerna y está orientado en dirección z. Sin embargo, debido al nodo esférico el signo algebraico de la función de onda cambia dentro de los dos lóbulos de la mancuerna. Finalmente consideremos los orbitales 3p x y 3p y. Tendrían la misma forma que el orbital 3p z, pero estarían orientados en la dirección x e y respectivamente. También podríamos pensar en qué pasaría con los orbitales p si aumentáramos aún más el número cuántico n. En este caso la forma de mancuerna permanecería, pero se introducirían nodos esféricos adicionales. Un orbital 4p tendría dos nodos esféricos, un orbital 5p tres nodos esféricos, y así sucesivamente. El tamaño de estos orbitales p también aumentaría con el número cuántico n.
El 3d z 2 Orbital
Ahora consideremos los orbitales con el número cuántico orbital l=2. Estos orbitales son los llamados orbitales d. Debido a que el número cuántico principal n siempre tiene que ser al menos un número entero mayor que el cuántico l, los d orbitales con el número cuántico menor n son los orbitales 3d. Para cada número cuántico n debe haber cinco d orbitales porque para l=2 el número cuántico magnético m puede adoptar los valores -2, -1, 0, -1, +1 y +2. Veamos primero el orbital 3d con m=0. A este orbital se le llama orbital 3d z 2. Su función de onda se muestra a continuación (Ec. 1.2.19).
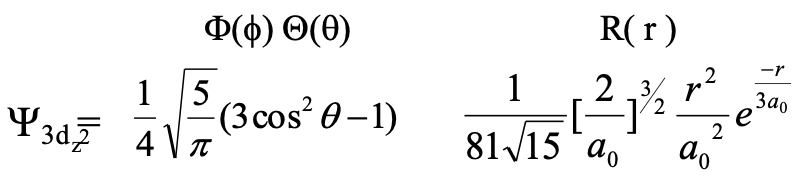
Ecuación 1.2.19 Función de onda para el orbital 3d z 2
Se puede ver que la función radial es producto de tres términos: una constante, un término r 2 /a 0 2, y el término exponencial e -r/3a 0. El término exponencial es el mismo que para los orbitales 3p. Debido al término r 2 /a 0 2 la amplitud de la función de onda es 0 en r=0. La amplitud entonces aumenta con r, pasa por un máximo, y luego se acerca a cero. Esto significa que la función de onda nunca cambia su signo algebraico, y por lo tanto no tiene nodos esféricos. La función de probabilidad radial tiene una forma similar en comparación con la función radial (Figura 1.2.30). La probabilidad de electrones está algo más alejada del núcleo en comparación con los orbitales 3p, lo que significa que el orbital 3d es algo mayor que el orbital 3p.
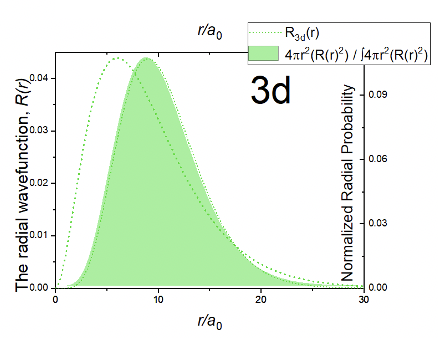
Se puede ver que la parte angular de la función de onda es una función de θ lo que significa que el orbital será no esférico y habrá al menos un nodo angular. En este caso los nodos angulares son dos nodos cónicos. Estos nodos describen dos conos que le dan al orbital su forma característica. Es un anillo de rosquilla en el plano xy alrededor de una mancuerna apuntando en dirección z. La mancuerna y la rosquilla tienen diferentes signos algebraicos indicados por diferentes colores (Figura 1.2.31). Tenga en cuenta que en contraste con los orbitales p los dos lóbulos de la mancuerna tienen el mismo signo algebraico.
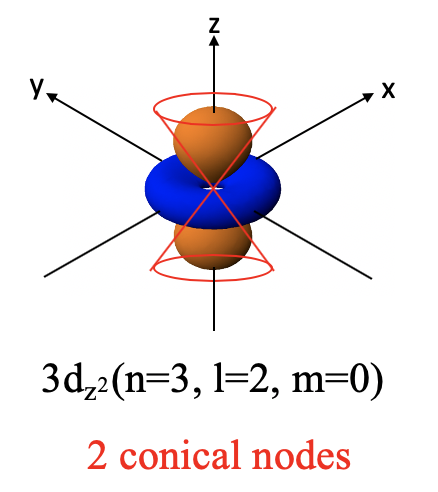
Podemos entender que el orbital 3d z 2 tiene dos nodos cónicos cuando convertimos la parte angular de la función de onda en coordenadas cartesianas (Eq. 1.2.20).
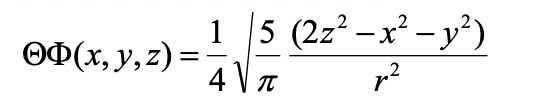
Ecuación 1.2.20 Parte angular de la función de onda del orbital 3d z 2 en coordenadas cartesianas.
Se puede ver que es una función de 2z 2 -x 2 -y 2. Esta es la forma matemática de los conos. La parte angular de la función de onda se convierte en 0 cuando 2z 2 =x 2 -y 2 lo cual es cierto en la superficie de dos conos, uno por encima del plano xy y otro por debajo del plano xy. El nombre del orbital 3d z 2 se debe a que es una función de z 2.
El Orbital 3d x 2 -y 2
Veamos a continuación el orbital 3d x 2 -y 2 (Eq. 1.2.21).
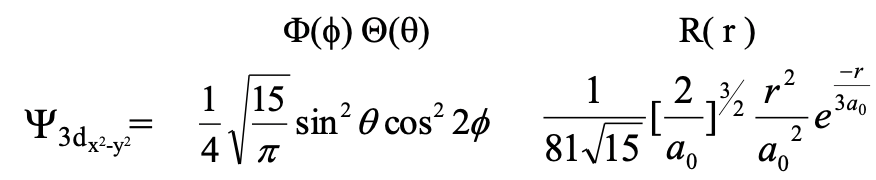
Ecuación 1.2.21 Función de onda para el orbital 3d x 2 -y 2
La parte radial de la función de onda es la misma que la del orbital 3d z 2. La parte angular de la función de onda es a la vez una función de θ y Φ y, por lo tanto, hay nodos angulares que esperar. Podemos encontrarlos de nuevo cuando convertimos la parte angular de la función de onda de coordenadas esféricas a cartesianas.
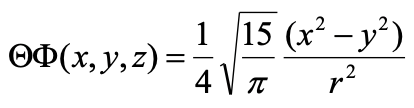
Ecuación 1.2.22 Parte angular de la función de onda del orbital 3d x 2 -y 2 en coordenadas cartesianas.
Se puede ver que la función angular es una función de x 2 -y 2. La función se vuelve cero cuando x 2 -y 2 =0. Este es el caso cuando x=y o x=-y. X es igual a y en dos líneas que bisecan el ángulo de 90 grados entre el eje x y. La coordenada z es completamente variable. Así, en general, la función de onda se convierte en cero en dos planos que se colocan perpendiculares al plano xy y bisecan el ángulo de 90 grados entre los ejes x e y. Estos dos planos son, por lo tanto, los dos nodos planos de la órbita.
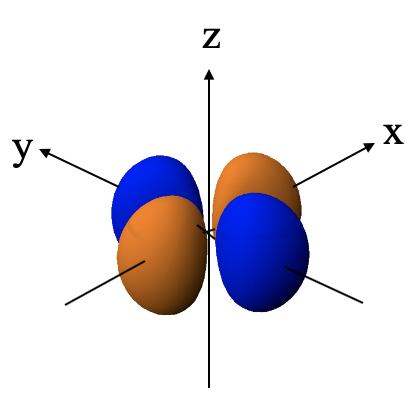
Debido a los dos nodos planos, la órbita tiene cuatro lóbulos que se encuentran en el eje x y, respectivamente. Los lóbulos que se encuentran en el eje x tienen el signo algebraico opuesto en comparación con los que se encuentran en el eje y. El nombre del orbital dx 2 -y 2 se debe a que es una función de x 2 -y 2.
Los orbitales 3d xy, 3d yz y 3d xz
Los orbitales d restantes son el 3d yz, el 3d xz y el 3d xy. La función radial de estos orbitales es igual a las que discutimos anteriormente. La parte angular de las funciones de onda se muestra aquí directamente en coordenadas cartesianas. El orbital d yz es una función de yz. La función se convierte en cero cuando y=0 o z=0. y es cero en el plano xz, y z es cero en el plano xy. Por lo tanto, estos planos son nodos planos de la órbita. Debido a estos nodos, el orbital tiene cuatro lóbulos que se encuentran en el plano yz donde los lóbulos están entre los ejes y y z. Tenga en cuenta que los lóbulos adyacentes tienen signo algebraico opuesto, y los lóbulos opuestos tienen el mismo signo algebraico.
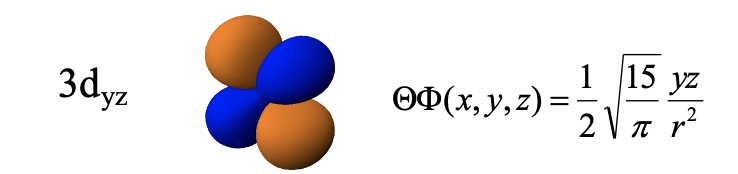
El orbital 3d xz es una función de xz, y así la función se convierte en cero con x=0 o z=0. Esto define que yz y los planos xy como los dos nodos planos. El orbital tiene la misma forma que el 3d yz, excepto que los cuatro lóbulos se encuentran dentro del plano xz en lugar del plano yz.
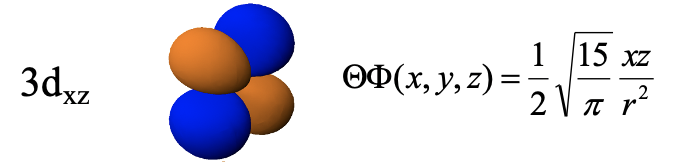
El 3d xy -orbital es una función de xy, y así su función de onda se convierte en cero en x=0 o y=0. Por lo tanto, los planos xz e yz son los nodos planos y el orbital tiene cuatro lóbulos en el plano xy entre los ejes x e y. Tenga en cuenta que el 3d xy y el 3d x 2 -y 2 se ven muy similares pero son diferentes. La diferencia es que el orbital 3d x 2 -y 2 tiene sus lóbulos en el eje x y, mientras que el orbital 3d xy tiene los lóbulos entre el eje x y el eje y. También se puede decir que el orbital 3d x 2 -y 2 se gira 45 grados alrededor de z con respecto al orbital 3d xy.
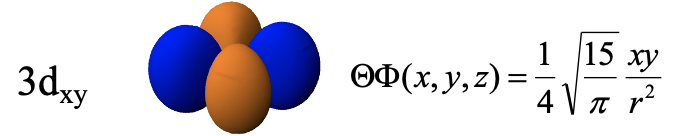
Reglas para nodos angulares y esféricos
Por supuesto, ahora podríamos discutir el tamaño y la forma de muchos otros orbitales como los orbitales 4d o los orbitales 4f, pero esto estará más allá del alcance. En cambio, pensemos si existen reglas generales que permitan la predicción del número de nodos esféricos y angulares en una órbita. El número de nodos radiales siempre es igual a n-l-1, el número de nodos angulares es igual a l, y el número total de nodos es siempre n-1. Esto significa que el número de nodos aumenta con el número cuántico n. Si aumentamos el número cuántico l para un número cuántico dado n, entonces reemplazamos los nodos esféricos por nodos angulares. Esto se resume en la Figura 1.2.36.

Las Energías Orbitales para el Átomo H
La ecuación de Schrödinger no sólo permite calcular los orbitales del átomo de hidrógeno, sino también sus energías. Las energías del modelo Bohr y Schrödinger coinciden: E = constante/n 2: Esto significa que los orbitales con el mismo número cuántico n tienen las mismas energías. Las energías no son una función de los números cuánticos l y m. Las energías son negativas porque son energías vinculantes. En otras palabras: Agregar un electrón a un protón es un proceso exotérmico. La energía de unión para la energía aumenta a medida que disminuye la energía orbital (Fig. 1.2.37).
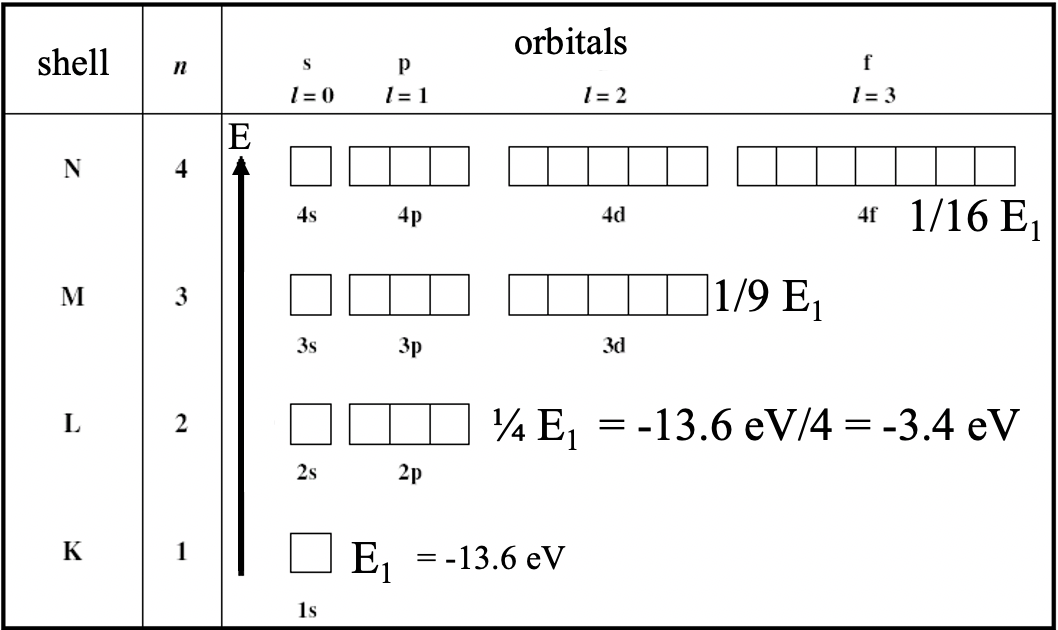
Para el orbital 1s de H la energía es -13.6 eV, la energía de los 2s y los orbitales 2p son ¼ de eso, la energía de los orbitales 3s, 3p y 3d son 1/9 de la energía del orbital 1s y así sucesivamente. Nota a ¼ y 1/9 de -13.6 eV es más de -13.6 eV debido al signo algebraico negativo. El electrón voltio es una unidad de energía. Es la cantidad de energía cinética que obtiene un solo electrón no unido cuando pasa a través de una diferencia de potencial electrostático de un voltio, en vacío.
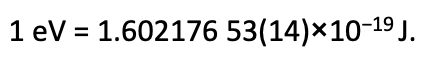
Ecuación 1.2.23 Conversión de unidades de electrón voltio a julio.
En otras palabras, es igual a un voltio (1 voltio = 1 julio por culombio) multiplicado por la carga de un solo electrón (en culombios). Se trata de una unidad de energía muy pequeña que es práctica para los cálculos de energía orbital porque las energías orbitales son muy pequeñas (Ec. 1.2.23).
Átomos multi-electrón
Hasta ahora sólo hemos considerado los orbitales para el átomo de hidrógeno que contiene un solo electrón. ¿Podemos también resolver la ecuación de Schrödinger para átomos que tienen más de un electrón y obtienen las energías exactas de los orbitales? La respuesta es no, esto matemáticamente no es posible. El proceso simplemente ya es demasiado complejo incluso para sólo dos electrones. La ecuación de Schrödinger solo se puede resolver para sistemas de un electrón. Por lo tanto, la descripción de la estructura atómica de todos los demás átomos debe funcionar con aproximaciones. Consideremos primero el átomo de Él. Tiene sólo un electrón más que el hidrógeno. Es un enfoque útil para aproximar átomos multi-electrón como sistemas de un electrón primero, y luego aproximar las interacciones electrón-electrón. Las energías de electrones en un átomo con más de un protón deben seguir la ecuación E n =-Z 2 x13.6 EV/n 2, donde Z es el número de protones.
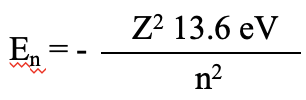
Ecuación 1.2.24 Las energías orbitales para átomos con más de un protón
La energía de unión del electrón aumenta proporcionalmente al cuadrado del número de protones porque las atractivas fuerzas de Coulomb que actúan sobre los electrones cargados negativamente aumentan con el número de protones cargados positivamente en el núcleo. Se pueden medir experimentalmente las energías orbitales a través de energías de ionización. La energía requerida para eliminar un electrón en un orbital particular del átomo es igual a la energía de unión para el electrón en ese orbital. Por lo tanto la energía de ionización IE = -E n (E n = energía orbital). Según el modelo de Schrödinger la energía orbital para un electrón de helio en un orbital 1s debe ser E 1s =- (2 2 ×13.6 eV) /1 1 =-54.4 eV (Ec. 1.2.25).
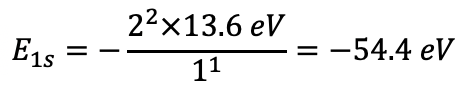
Ecuación 1.2.25 Energía para un electrón de helio en un orbital 1s.
Sin embargo, la energía de ionización medida experimentalmente del electrón es de +24.6 eV, lo que significa que la energía orbital real es de -24.6 eV, y no -54.4 eV. Por otro lado, la ionización de un ion He + es de +54.4 eV que es exactamente lo que esperaríamos. Podemos explicar este fenómeno por el hecho de que el modelo de Schrödinger funciona solo para un solo electrón y debe descuidar las interacciones electrónicas. En un ion He + solo hay un electrón, por lo tanto el modelo de Schrödinger predice correctamente la energía del electrón. Sin embargo, en un átomo de helio hay dos electrones, y el modelo de Schrödinger no puede dar cuenta de las interacciones electrón-electrón. Por lo tanto, no da la energía correcta para los electrones en un átomo de helio. Las interacciones electrón-electrón se pueden ver como efectos de blindaje. Esto significa que el primer electrón protege parte de la carga nuclear del segundo electrón. Por lo tanto, el segundo electrón experimenta una fuerza Coulomb reducida del núcleo. Debido a la fuerza reducida de Coulomb, la energía de unión es menor. Se reduce de -54.4 eV a -24.6 eV. Cabe señalar que los dos electrones en el orbital 1s del átomo de He son indistinguibles, es decir, ambos tienen la energía de unión reducida. La energía de unión solo aumenta a -54.4 eV después de que se haya eliminado uno de los dos electrones.
La carga positiva neta del núcleo después de contabilizar los efectos de blindaje se llama carga nuclear efectiva. Para el átomo de helio la carga nuclear efectiva es de 1.34. Podemos calcular la carga nuclear efectiva a partir de la primera energía de ionización medida experimentalmente. Resolver la ecuación para Z eff da Z eff =1.34 (Ec. 1.2.26).
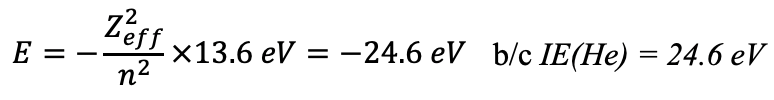
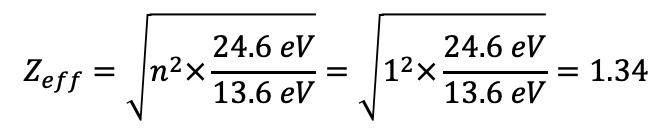
Ecuación 1.2.26 Cálculo de Z eff en el átomo de helio a partir de las primeras energías de ionización.
El átomo de litio
Ahora vayamos al átomo con tres electrones, el átomo de litio. Siguiendo el llamado principio de Aufbau llenaríamos los dos primeros electrones en el orbital 1s, porque el orbital 1s es el orbital con la energía más baja. Sin embargo, el tercer electrón no encaja en el orbital 1s debido al principio Pauli.

El principio Pauli establece que no hay dos electrones en un átomo que pueda tener los mismos cuatro números cuánticos. Por esa razón un orbital no puede acomodar más de dos electrones. Dentro de un orbital dos electrones deben tener diferentes números cuánticos de espín s. Podemos indicarlo escribiendo los electrones como flechas apuntando hacia arriba y hacia abajo en una caja cuadrada que representa el orbital. El tercer electrón del litio tendría que ir a la órbita con la siguiente energía más alta.

Según el modelo de Schrödinger, la energía de un orbital es sólo una función del número cuántico n, y tendríamos dos opciones: los orbitales 2s y 2p. Ambos tendrían la misma energía. Sin embargo, en el átomo de litio el orbital 2s tiene una energía algo menor que el orbital 2p. Esto puede explicarse nuevamente por los efectos de blindaje. El orbital 2s penetra en el orbital 1s ligeramente mejor que los orbitales 2p. Debido a eso, el orbital 1s protege la carga nuclear del núcleo menos para el orbital 2s en comparación con los orbitales 2p. La configuración electrónica del estado fundamental, que es la configuración de electrones atómicos que tiene la energía más baja, debe ser, por lo tanto, 1s 2 2s 1. Podemos ver que el orbital 2s penetra en el orbital 1s ligeramente mejor que el orbital 2p de la gráfica para las funciones de probabilidad radial de los orbitales mostrados en la Figura 1.2.40.
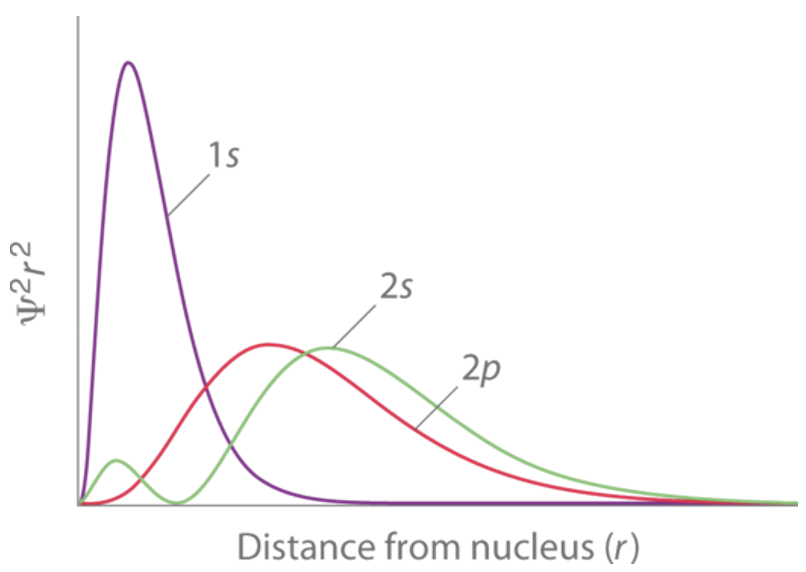
El segundo máximo grande de la función del orbital 2s está en realidad más alejado del núcleo en comparación con el máximo asociado con el orbital 2p. Sin embargo, debido a que el orbital 2s tiene un segundo máximo pequeño muy cerca del núcleo, el orbital 2s en general penetra mejor en el orbital 1s y, por lo tanto, el efecto de blindaje del orbital 1s en el orbital 2s es menor en comparación con los orbitales 2p.
Generalmente podemos decir, cuanto menor sea el número cuántico l para un número cuántico dado n, mejor será la capacidad de penetración de este orbital. Debido a la mejor capacidad de penetración, el blindaje es menor y así la carga nuclear efectiva que actúa sobre el electrón en la órbita es mayor. La mayor carga nuclear efectiva conduce a una menor energía de este orbital. Por esa razón la secuencia energética de orbitales con el mismo número cuántico n aumenta de s a p a d a f.
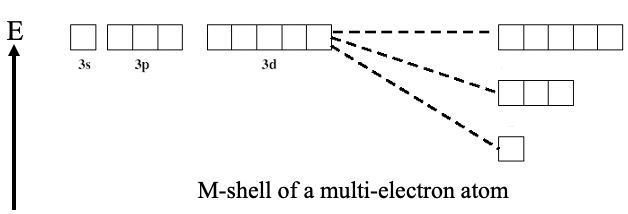
Por ejemplo, un orbital 3s tiene una energía menor que un orbital 3p que tiene una energía menor que un orbital 3d (Fig. 1.2.41).
Reglas de Slater
Debido a que una energía orbital puede calcularse a partir de la carga nuclear efectiva, sería útil que la carga nuclear efectiva pudiera estimarse de alguna manera mediante simples aproximaciones.

Las llamadas reglas de Slater, que llevan el nombre de su desarrollador John C. Slater (Fig. 1.2.42), son una herramienta sencilla que dan una buena estimación de la carga nuclear efectiva de orbitales en átomos multielectrónicos. Las reglas de Slater estiman una constante de blindaje σ que permite calcular la carga nuclear efectiva Z eff a partir de la carga nuclear de acuerdo con Z eff =Z-σ.
Las reglas para la estimación de σ son las siguientes. En primer lugar, debemos reconocer que las reglas para los electrones s y p son ligeramente diferentes a las de los electrones d y f. Esto se debe a que los electrones s y p del mismo número cuántico n tienen capacidades de penetración algo mayores en comparación con los electrones d y f. Para ambos grupos el primer paso es el mismo. Escribimos la configuración electrónica del átomo de acuerdo a sus números cuánticos n y l como se muestra a continuación (Fig. 1.2.43).

Tenga en cuenta que este orden no refleja exactamente el orden de la energía. Los electrones que tienen efectos de blindaje similares se agrupan entre paréntesis. Se puede ver que los orbitales s y p del mismo número cuántico n construyen un grupo, todos los demás orbitales son su propio grupo.
Para estimar la constante de blindaje para un orbital s o p ahora podemos aplicar las siguientes reglas:
a) Los electrones a la derecha del grupo (ns, np) no aportan nada a σ. Esto se debe a que estos electrones están más alejados del núcleo que del electrón de consideración.
b) Cada uno de los otros electrones del mismo grupo (ns, np) aporta 0.35 a σ. Estos electrones están en la misma capa que el electrón de consideración, y por lo tanto tienen una distancia similar al núcleo. Por esta razón su blindaje es solo modesto y puede estimarse en alrededor del 35% de una carga elemental completa, o 0.35.
c) Cada electrón en el caparazón n-1 aporta 0.85 a σ. Esos electrones están significativamente más cerca del núcleo en comparación con el electrón de consideración. Por esa razón blindan significativamente mejor, aproximadamente 85% de una carga elemental, o 0.85.
d) Cada electrón en el caparazón n-2 o inferior contribuye 1.00 a σ. Esos electrones están mucho más cerca del núcleo que el electrón de consideración y pueden blindar completamente una carga elemental. Por lo tanto, su contribución a la constante de blindaje se aproxima a 1.
Ahora veamos las reglas de Slater para los electrones d y f.
a) Los electrones a la derecha del grupo (nd) o (nf) no aportan nada a σ. Esto se debe nuevamente a que el electrón está más alejado del núcleo que el electrón de consideración, y por lo tanto no puede contribuir al blindaje.
b) Cada uno de los otros electrones del mismo (nd) o (nf) grupo aporta 0.35 a σ. Esto se debe nuevamente a que estos electrones tienen una distancia similar en comparación con el electrón para el cual calculamos la constante de blindaje, y así el blindaje es modesto.
c) Cada electrón a la izquierda del grupo (nd) o (nf) aporta 1 a σ. Esos electrones se consideran mucho más cercanos al núcleo, y así blindan una carga elemental completa.
Obsérvese que los valores 0.35, 0.85 y 1 han sido elegidos para que los resultados de las reglas de Slater estén en la mejor conformidad posible con las mediciones experimentales de energías orbitales. Recuerde, cuando discutimos el átomo de helio dijimos que la medición de las energías de ionización puede proporcionar energías orbitales experimentales.
Reglas de Slater aplicadas a átomos de electrones múltiples
Practicemos las reglas de Slater con algunos ejemplos. Podemos, por ejemplo, calcular la carga nuclear efectiva que actúa sobre un electrón 2p en un átomo de oxígeno. Para responder a esta pregunta necesitamos primero escribir la configuración electrónica de acuerdo con los números cuánticos n y l y agrupar los orbitales correctamente (Fig. 1.2.44).
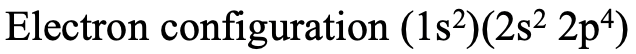
A continuación, debemos considerar que la carga nuclear efectiva Z eff es la carga nuclear Z menos la constante de blindaje σ. Entonces, debido a que el oxígeno tiene ocho protones, la carga nuclear es de 8. De eso necesitamos restar la constante de blindaje. En primer lugar, necesitamos darnos cuenta de que hay 5 electrones en el mismo grupo que el electrón 2p de consideración. Estos son los dos electrones 2s y los otros tres electrones 2p. Estos cinco electrones blindan con un factor de 0.35 porque están en el mismo grupo que el electrón 2p para el cual queremos calcular la constante de blindaje. Tenga en cuenta que este cuarto electrón 2p no obtiene un factor porque es el electrón para el cual calculamos la constante de blindaje. Además, hay que considerar los dos electrones 1s. Están en una concha n-1, por lo tanto contribuyen con un factor de 0.85. En general, la carga nuclear efectiva en el electrón 2p es 8- (2 x 0.85) - (5 x 0.35) = 4.55 (Fig. 1.2.45).
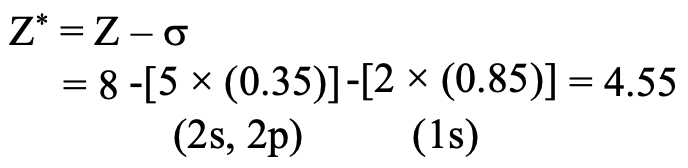
También podemos preguntar cuál es la carga nuclear efectiva sobre un electrón 1s en el átomo de oxígeno. Es 8-0.35=7.65 (Fig. 1.2.46).
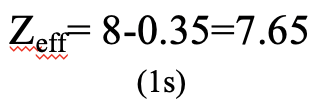
Esto se debe a que solo necesitamos considerar el segundo electrón en el orbital 1s para calcular la constante de blindaje σ. Contribuye con un factor de 0.35 porque se encuentra en el mismo grupo que el electrón 1s de consideración. Los electrones 2s y 2p están en un grupo derecho al orbital 1s, por lo tanto no contribuyen al blindaje.
Las reglas de Slater y el principio de Aufbau
Las reglas de Slater son de gran ayuda para entender el llamado principio Aufbau, que dice que para un átomo en el estado fundamental los electrones están en los orbitales de la energía más baja. Hasta cierto punto las energías orbitales siguen el número cuántico n, pero no siempre es así. Por ejemplo, el elemento potasio tiene la configuración electrónica 1s 2 2s 2 2p 6 3s 2 3p 6 3d 0 4s 1 y no 1s 2 2s 2 2p 6 3s 2 3p 6 3s 2 3p 6 3d 1. Esto significa que la energía del orbital 3d debe ser mayor que la energía del orbital 4s. ¿Pueden las reglas de Slater predecir eso? Por lo tanto, calculemos la energía del orbital 3d y 4s usando las reglas de Slater, y veamos si la energía del orbital 3d sale más alta que el electrón del orbital 4s.
Para el orbital 3d, la constante de blindaje es 18x1=18 porque hay 18 electrones además del electrón 3d de consideración, y todos los 18 electrones están en una capa inferior. Por lo tanto, todos contribuyen con un factor de 1. La carga nuclear Z del potasio es 19. Por lo tanto, la carga nuclear efectiva Z eff = 19-18=1 (Fig. 1.2.47).

Ahora hagamos el cálculo análogo para el electrón 4s. Para el electrón 4s se aplican las reglas de Slater para s electrones. Según eso, los dos electrones 3s y los seis 3p aportan 0.85 a la constante de blindaje porque están en una concha n-1. Los dos electrones restantes 1s, dos 2s y seis 2p están en una capa n-2 o inferior y por lo tanto contribuyen con el factor de 1. Por lo tanto, la constante de blindaje total es de 8 x 0.85 + 10 x 1 = 16.8. Por lo tanto, la carga nuclear efectiva Z eff es 19-16.8=2.2 (Fig. 1.2.48).
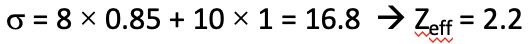
Podemos ver que una carga nuclear efectiva más alta actúa sobre un electrón 4s en comparación con un electrón 3d, lo que indica que la energía orbital para el electrón 4s será menor en comparación con el electrón 3d. Podemos calcular las energías orbitales usando la fórmula E= (Z eff 2) /n 2 ×13.6 eV (Ec. 1.2.27).
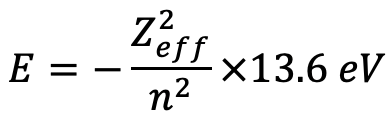
Ecuación 1.2.27 Ecuación para energías orbitales
Para el electrón 3d insertamos Z eff =1 y n=3 lo que da -1.51 eV, Eq. 1.2.28.
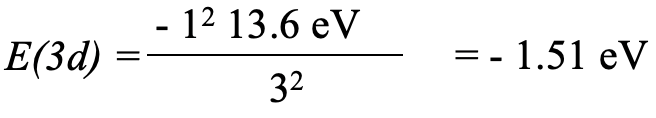
Ecuación 1.2.28 Ecuación para la energía orbital del electrón 3d de potasio
Para el inserto de electrones 4s Z eff =2.2 y n=4 lo que da -4.14 eV.

Ecuación 1.2.29 Ecuación para la energía orbital del electrón 4s de potasio
Como era de esperar, la energía del electrón 4s es menor que la energía del electrón 3d. Esto explica por qué se prefiere la configuración electrónica con el electrón 4s como el electrón de valencia sobre aquella con el electrón 3d como electrón de valencia. En general, podemos ver que las reglas de Slater pueden predecir correctamente las configuraciones electrónicas de los átomos y el principio de Aufbau.
Hagamos otro ejemplo más complejo: Hay dos configuraciones de electrones concebibles para el Fe. Uno en el que el subshell 4s se rellena antes que el subshell 3d, y otro en el que el subshell 3d se rellena antes que el subshell 4s. Para el primer caso la configuración electrónica es 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 6. Para el segundo caso, la configuración del segundo electrón es 1s 2 2s 2 2p 6 3s 2 3p 6 3d 8 4s 0. Podemos ver que las dos configuraciones de electrones son las mismas para los electrones 1s, 2s, 2p, 3s y 3p. Por lo tanto, nos enfocamos en los ocho electrones restantes, denotados en rojo, y calculamos sus energías.
En este caso, necesitamos comparar la suma de las energías de electrones para ambas configuraciones de electrones para poder decidir qué configuración de electrones es favorecida. Calculamos la suma de las energías de los ocho electrones para la configuración del primer electrón de la siguiente manera: En el primer paso necesitamos reescribir la configuración electrónica en forma Slater: (1s 2) (2s 2 2p 6) (3s 2 3p 6) (3d 6) (4s 2).
A continuación, podemos calcular la constante de blindaje para un electrón 3d. Podemos ignorar los dos electrones 4s porque están a la derecha del electrón d de consideración, y no contribuyen al blindaje. Sin embargo, sí necesitamos considerar los otros cinco electrones 3d que están en el mismo grupo que el electrón 3d de consideración. Aportan con el factor de 0.35. Los otros 18 electrones aportan 1.00 porque están en una capa inferior. Debido a que la carga nuclear efectiva de Fe es 26, la carga nuclear efectiva Z eff es Z eff =26-19.75=6.25 (Eq. 1.2.30).
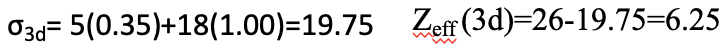
Ecuación 1.2.30 Ecuación para la constante de blindaje y la carga nuclear efectiva del electrón 3d de un átomo de hierro
Para un electrón 4s, hay otro electrón 4s en el mismo grupo que contribuye con un factor de 0.35. Además, hay 14 electrones en un caparazón n-1, es decir, los electrones 3s, 3p y 3d. Aportan 0.85 a la constante de blindaje. Los 10 electrones restantes están en una capa n-2 o inferior, por lo que contribuyen con el factor 1.00. Esto da una constante de blindaje general de 22.25. A partir de eso podemos calcular la carga nuclear efectiva para un electrón 4s que es 26-22.25=3.75.
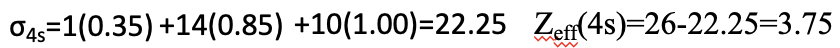
Ecuación 1.2.31 Ecuación para proteger la carga nuclear constante y efectiva del electrón 4s de un átomo de Fe
Ahora podemos calcular las energías de los electrones. Es la suma de las energías para los electrones 3d y 4s. La energía electrónica para un solo electrón es E=- (Z eff 2) /n 2 ×13.6 eV= - (6.25 2) /3 2 ×13.6 eV=-59.03 eV. Debido a que tenemos seis electrones 3d, la energía general para los seis electrones es de 6 x -59.03 eV = -354.17 eV (Eq. 1.2.32).
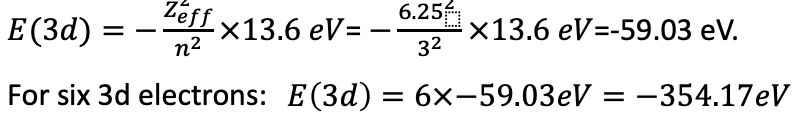
Ecuación 1.2.32 Ecuación para las energías de electrones de los seis electrones 3d en un átomo de hierro
La energía de un solo electrón 4s es E=- (3.75 2) /4 2 ×13.6 EV=-11.95 eV. Para dos electrones 4s la energía es de 2 x -11.95 eV= -23.90 eV.
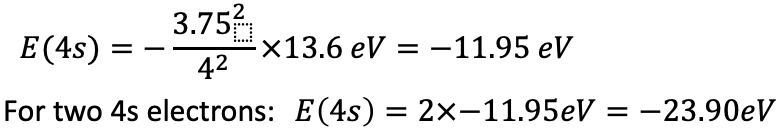
Ecuación 1.2.33 Ecuación para las energías de electrones del electrón 4s en hierro
La suma de todos los electrones es entonces -354.17 eV + (-23.90 eV) = -378.1 eV (Eq. 1.2.34).
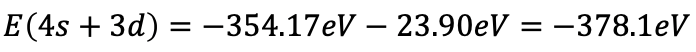
Ecuación 1.2.34 Ecuación para la suma de todos los electrones
Ahora calculemos la energía para la configuración del segundo electrón. Primero necesitamos esta configuración de electrones en configuración de Slater. A continuación, podemos calcular la constante de blindaje para los d electrones. Es σ 3d = 7 (0.35) + 18 (1.00) = 20.45 porque hay otros siete electrones 3d en el mismo grupo y 18 electrones en conchas inferiores. La carga nuclear efectiva es entonces Z eff (3d) = 26- 20.45 = 5.55.
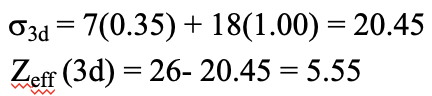
Ecuación 1.2.35 Ecuación para la constante de blindaje y la carga nuclear efectiva de los electrones 3d de hierro (segunda configuración)
La suma de las energías electrónicas para los ocho electrones d es entonces E (σ 3d) =-8 (5.55 2 /3 2) EV=-372.3 eV, Eq. 1.2.36.
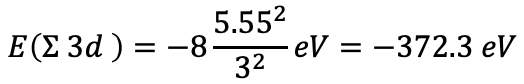
Ecuación 1.2.36 Ecuación para la suma de las energías de electrones para los ocho electrones d de hierro
Podemos ver que la energía de la configuración del segundo electrón es algo mayor, y por lo tanto menos preferida. Esto está de acuerdo con la configuración electrónica del estado fundamental observada experimentalmente del átomo de Fe. Nuevamente, vemos que las reglas de Slater pueden predecir correctamente la configuración electrónica del estado fundamental de los átomos.
El principio de Aufbau y la energía de emparejamiento de espín
Las reglas de Slater son adecuadas para dar cuenta de los efectos de blindaje en átomos de electrones múltiples que son de naturaleza electrostática. Sin embargo, no solo los efectos electrostáticos influyen en las energías orbitales, también hay efectos magnéticos. Esto se debe a que cada electrón tiene un espín con un campo magnético asociado a él. Los electrones se comportan como pequeños imanes que pueden interactuar entre sí. Estas interacciones pueden ser atractivas o repulsivas, lo que influye en las energías de los electrones. Las energías de electrones suelen minimizarse cuando se maximiza el número de electrones con el mismo espín. Esto se conoce como regla de Hund (Fig. 1.2.49) de multiplicidad máxima de giro.

En el ejemplo anterior hemos visto que la configuración de electrones 4s 2 3d 6 se ve favorecida en Fe debido a los efectos de blindaje electrostático. Además, también favoreció por los efectos magnéticos. En esta configuración electrónica hay cuatro electrones desapareados, mientras que en la configuración electrónica 3d 8 solo hay dos electrones desapareados.
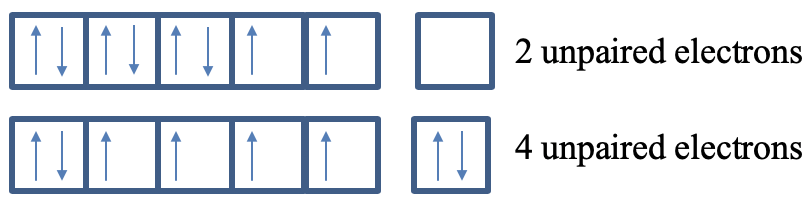
Ahora podemos entender el principio de Aufbau para los átomos de múltiples electrones (Figura 1.2.51).
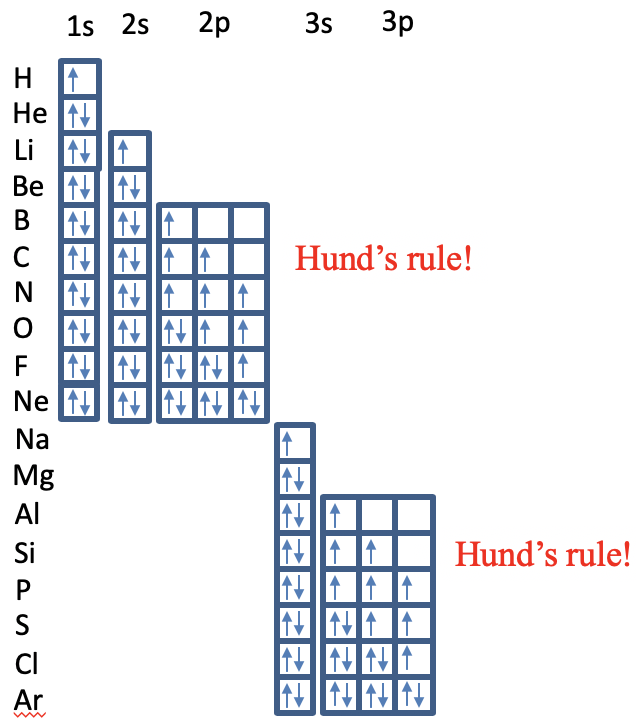
Para H y He se llena el orbital 1s. Del litio al berilio la subcapa 2s se llena, y del boro al neón la subcapa 2p se llena bajo consideración de la regla de Hund. Se puede ver que para el carbono los dos electrones 2p son ambos spin up en diferentes orbitales 2p. Para el nitrógeno hay tres electrones desapareados en los orbitales 2p. A partir del elemento oxígeno, tenemos que comenzar a emparejar giros hasta que todos los giros estén emparejados en neón. De Na a Ar los orbitales 3s y 3p se llenan según los mismos principios.
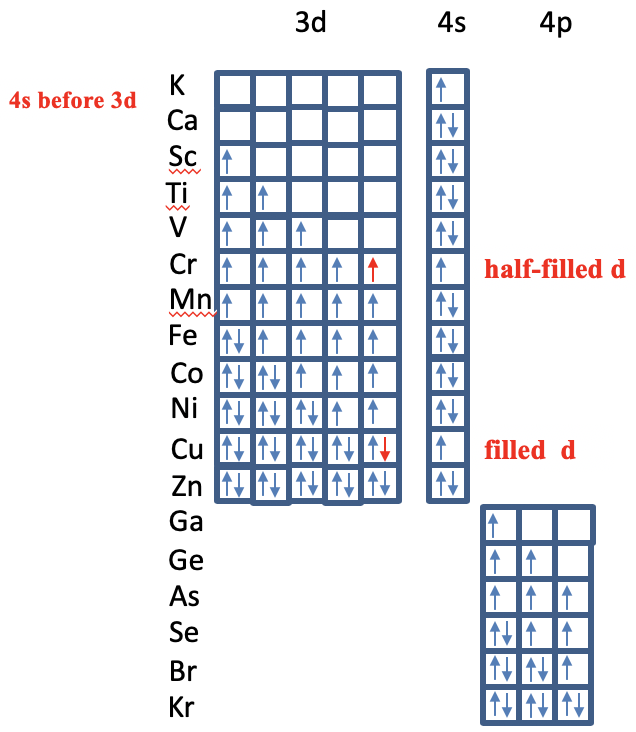
Después de eso, los orbitales 4s de K y Ca se llenan, y luego los orbitales 3d de los elementos de Sc a Zn (Fig. 1.2.52). Hemos visto anteriormente que las reglas de Slater muestran amablemente por qué. Se puede ver que hay dos anomalías sin embargo. Para el cromo, la configuración electrónica es 4s 1 3d 5 y no 4s 2 3d 4. Esto se debe a que hay más espines desapareados en esta configuración de electrones, y una subcapa 3d medio llena con espines desapareados solo representa una configuración de electrones particularmente estable. La segunda anomalía ocurre para el elemento Cu que tiene una configuración electrónica 4s 1 3d 10 y no 4s 2 3d 9. Esto se debe a que una configuración de electrones d 10 es una configuración de electrones estable particular. Después de llenar el subshell 3d, el subshell 4p se rellena para los elementos de Ga a Kr. Nuevamente, los electrones se llenan en los orbitales según la regla de Hund. Podríamos extender nuestra consideración a elementos aún más pesados, pero quedaremos más allá del alcance.


