2.3: Representaciones matriciales de operaciones de simetría y tablas de caracteres

Representaciones matriciales de operaciones de simetría

Por lo tanto, hasta ahora hemos mirado cualitativamente las operaciones de simetría, y determinado su naturaleza por inspección. Ahora echemos un vistazo a cómo podemos describir las operaciones de simetría desde un punto de vista más matemático. ¿Por qué hacemos esto? Esto lo hacemos para poder entender las llamadas tablas de caracteres que posteriormente necesitaremos aplicar simetría a la teoría orbital molecular. Generalmente, las operaciones de simetría pueden describirse mediante matrices. Cuando una matriz que representa una operación de simetría se multiplica por las coordenadas de un objeto, entonces esto da las nuevas coordenadas del objeto después de que se realizó la operación de simetría. Por lo tanto, revisemos brevemente las matrices, y las multiplicaciones de matrices en particular. Una matriz no es más que una matriz de números dispuestos en filas y columnas. Cuando multiplicamos a matrices, debemos multiplicar cada fila con cada columna de la matriz. Cuando la primera matriz A _ik tiene i filas y k columnas y la segunda matriz B _kj tiene k filas y j columnas, entonces la matriz de producto C _ij tiene i filas y j columnas. Un requisito para una multiplicación matricial es que el número de columnas de la primera matriz sea el mismo que el número de filas de la segunda columna. De lo contrario, uno simplemente no puede multiplicar cada fila con cada columna de las dos matrices.

Figura 2.3.1 Revisión sobre la multiplicación de matrices

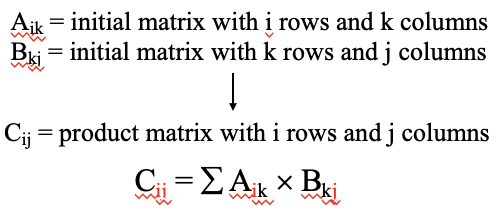
Hagámoslo con algunos ejemplos.

Ejemplo 1 de Multiplicación Matricial

En el primer ejemplo multiplicamos dos matrices 2x2, es decir, que ambas tienen dos filas y dos columnas (Fig. 2.3.2). Primero, tenemos que verificar si las dos matrices se pueden multiplicar. Podemos ver que las columnas numéricas de la primera matriz es 2, y el número de filas de la segunda matriz también es 2. Por lo tanto, podemos multiplicar las dos matrices.

Figura 2.3.2 Ejemplo 1 de multiplicación matricial

Se espera que la matriz del producto sea también una matriz 2x2. Ahora necesitamos multiplicar la primera fila de la primera matriz con la primera columna de la segunda matriz, y eso significa que vamos a multiplicar 1x7 y 5x4. La suma de 1x7+5x4=27 nos da el primer carácter de la primera fila de la matriz del producto. A continuación, multiplicamos la primera fila de la primera matriz con la segunda columna de la segunda matriz. Entonces tenemos que multiplicar 1x3 y 5x8. La suma de los dos productos da el segundo carácter de la primera fila de la matriz de productos. Debido a que la segunda matriz no tiene columna adicional, no hay otra columna con la que se pueda multiplicar la primera fila de la primera matriz. Por lo tanto, ahora vamos a la segunda fila de la primera matriz, y la multiplicamos por la primera columna de la segunda matriz. Esto le da a los productos 2x7 y 6x4. Cuando se suman, entonces esto da 38, y este es ahora el primer carácter de la segunda fila de la matriz de productos. Por último, multiplicamos la segunda fila de la primera matriz por la segunda fila de la segunda matriz. Esto da 2x3 y 6x8 que da 54 cuando se suman. Este es el segundo carácter en la segunda fila de la matriz del producto.

Ejemplo 2 de Multiplicación Matricial

En el siguiente ejemplo, multiplicamos una matriz de 1x3 por una matriz de 3x3 (Fig. 2.3.3). Esto es posible porque el número de las columnas de la segunda matriz es 3, y el número de filas de la segunda matriz también es 3.

Figura 2.3.3 Ejemplo 2 de multiplicación matricial

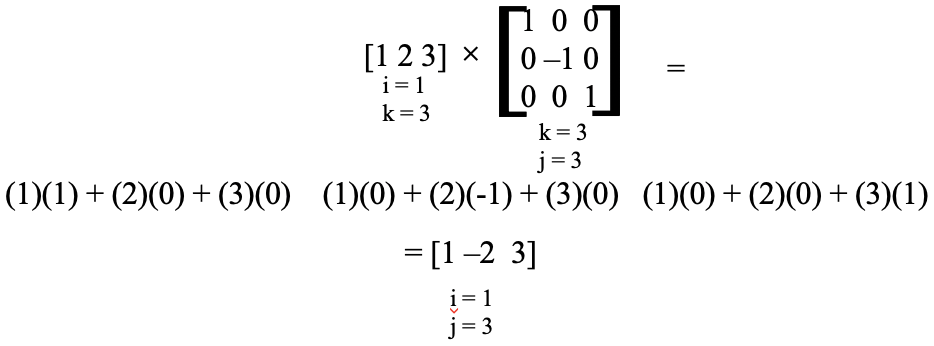
Se esperaría que la matriz del producto tuviera una fila y tres columnas. La primera matriz tiene sólo una fila, por lo que la multiplicamos con las tres columnas de la segunda matriz. Multiplicar la primera fila de la primera matriz con la primera columna de la segunda matriz da (1) (1) + (2) (0) + (3) (0) = 1. Este es el primer carácter en la primera, y la única fila en la matriz del producto. La multiplicación de la primera fila de la primera matriz con la segunda columna de la segunda matriz es (1) (0) + (2) (-1) + (3) (0) = -2 que es el segundo carácter de la primera fila de la matriz de producto. La multiplicación de la primera fila de la primera matriz con la tercera columna de la segunda matriz da (1) (0) + (2) (0) + (3) (1) = 3. Este es el tercer carácter de la primera fila de la matriz del producto. En general, la matriz del producto es [1 -2 3].

Ejemplo 3 de Multiplicación Matricial

En el último ejemplo vamos a multiplicar una matriz de 3x3 por una matriz de 3x1 (Fig. 2.3.4). Nuevamente, el número de las columnas de la primera matriz es el mismo que el número de las filas de la segunda matriz, ambas son 3. Así, podemos multiplicar las dos matrices.

Figura 2.3.4 Ejemplo 3 de multiplicación matricial

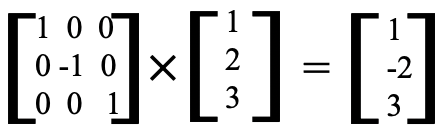
Multiplicando la primera fila de la primera matriz por la primera, y en este caso solo columna de la segunda matriz da 1x1 + 0x2 + 0x3 = 1. Este es el primer y único carácter de la primera fila de la matriz de productos. La segunda matriz tiene sólo una columna, por lo tanto multiplicamos la segunda fila de la primera matriz con la única columna de la segunda matriz en el siguiente paso. Esto da 0x1 + (-1) x2 + 0x3 = -2. Este es el carácter de la segunda fila de la matriz del producto. Por último, multiplicamos la tercera fila de la primera matriz por la columna de la segunda matriz. Esto da 0x1 + 0x2 + 1x3 = 3. Este es el carácter de la tercera fila de la matriz del producto.

Aplicación de multiplicaciones matriciales a operaciones de simetría

Entonces, ¿qué tienen que ver las operaciones de simetría con la multiplicación de matrices? La respuesta es que una operación de simetría puede describirse como una matriz, y la multiplicación de esta matriz con la matriz que representa las coordenadas de la posición de los puntos en un objeto, dará las nuevas coordenadas del objeto después de que se haya realizado la operación de simetría (Fig. 2.3.5).

Figura 2.3.5 Relaciones entre operaciones de simetría y matrices

Ejemplo H ₂ O

Una matriz que representa una operación de simetría es una matriz 3x3 y la matriz que describe coordenadas es una matriz 3x1. Cuando dos se multiplican entonces esto da una matriz 3x1 que describe las nuevas coordenadas del objeto. Por ejemplo, veamos la molécula de agua H ₂ O.

Figura 2.3.6 Transformación de coordenadas en H ₂ O tras la aplicación de la operación de simetría _C2

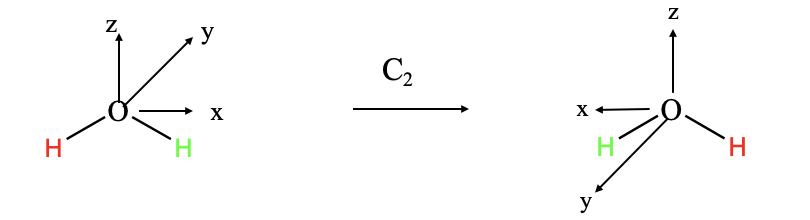
Podemos definir un sistema de coordenadas en la molécula de agua para que la molécula esté dentro del plano xz, por lo que se elige el eje z para que bisecta el ángulo de enlace H-O-H. El eje y se colocaría perpendicular y apuntaría hacia el plano de la placa (Fig. 2.3.6). Cualquier punto dentro de la molécula de agua, tendría coordenadas x, y, z que están definidas por vectores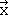,,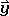 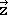que apuntan a estas coordenadas. Por ejemplo, el centro de un átomo de hidrógeno particular tendría coordenadas específicas que serían descritas por tres vectores que al sumarse, apuntarían al centro del átomo de hidrógeno. Ahora pensemos cómo van a cambiar las coordenadas a medida que llevemos a cabo unas operaciones de simetría específicas. Por ejemplo, tomar la operación de simetría C ₂ que se realiza alrededor del eje z. ¿Cómo cambiará la rotación, las coordenadas x, y y z, respectivamente?

La coordenada x se define por un vector que apunta hacia la dirección x. A medida que giramos este vector 180° alrededor del eje z, conservará su longitud pero apuntará en dirección opuesta (Fig. 2.3.6). De ahí que podamos decir que la coordenada x ha cambiado su signo algebraico, y ahora es —x. ¿Y ahora qué pasa con la coordenada y? Un vector que apunta en la dirección y también se girará alrededor de 180° y apuntará en la dirección opuesta. Eso significa que es —y después de la ejecución de la operación de simetría. Por último, ¿cómo cambiará la coordenada z? Debido a que giramos alrededor de z, no habrá ningún cambio en el vector z, y así la nueva coordenada z será idéntica a la antigua coordenada z Si representamos los tres vectores de las coordenadas antiguas por una matriz 3x1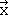,,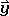, 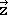las nuevas coordenadas de la matriz 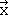', ',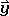' 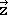están representados por la matriz -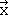, -,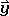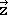. La matriz que al multiplicarse por la matriz para las coordenadas antiguas da la matriz para las nuevas coordenadas, sería la matriz que representaría la operación de simetría _C2. En el caso de la operación de simetría C ₂ la matriz tiene la forma siguiente (Fig. 2.3.7).

Figura 2.3.7 Operación de simetría C ₂ para H ₂ O en forma de matriz

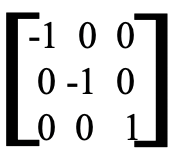
Podemos demostrar que esta matriz representa correctamente la operación de simetría _C2 aplicando las reglas de multiplicación para matrices. Multiplicar la primera fila de la matriz para C ₂ con la única columna de la matriz para las coordenadas antiguas daría (-1 x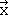) + (0 x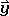) + (0 x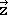) = - 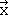para el primer carácter de la matriz del producto. Multiplicar la segunda fila de la representación matricial de C ₂ con la única columna de la matriz para las coordenadas antiguas da (0 x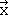) + (-1 x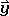) + (0 x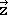) = - 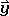para el segundo carácter de la matriz del producto. La multiplicación de la tercera fila de la matriz para C ₂ con la columna de la matriz para las coordenadas antiguas da (0 x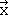) + (0 x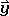) + (1 x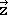) = 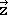Esto demuestra que la matriz representa correctamente la operación de simetría _C2.

Figura 2.3.8 La operación de simetría _C2 en forma de matriz transformando las coordenadas en H ₂ O

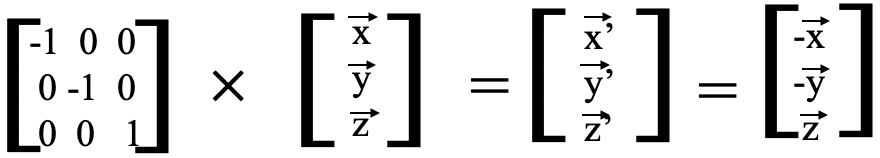
Podemos desarrollar la representación matricial para la operación de reflexión σ (xz) a lo largo de la misma línea que hicimos para la operación C ₂. Pensemos primero en cómo cambian los vectores que representan la coordenada a medida que se lleva a cabo la operación de reflexión. Los vectores y no cambian porque están dentro del plano espejo xz. Sin embargo, el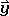 vector cambia su dirección a medida que se refleja hacia el otro lado del plano espejo. Así, la coordenada y cambia su signo algebraico.

Figura 2.3.9 Transformación de coordenadas de H ₂ O tras la aplicación de la operación de simetría σ _xz

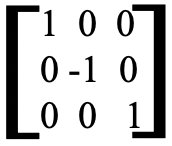
Por lo tanto, la matriz que representa las nuevas coordenadas tiene la forma, -,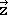. La matriz que cuando se multiplica por la matriz de las coordenadas antiguas, da la matriz de las nuevas coordenadas debe ser la matriz que representa la operación de simetría σ _xz. Tiene la siguiente forma (Fig. 2.3.10).

Figura 2.3.10 operación de simetría σ _xz en H ₂ O en forma de matriz

Podríamos mostrar nuevamente usando las reglas de multiplicación para matrices que la multiplicación de esta matriz con la matriz para las coordenadas antiguas da la matriz para las nuevas coordenadas (Fig. 2.3.11).

Figura 2.3.11 la operación de simetría para σ _xz en forma de matriz transformando las coordenadas de H ₂ O.

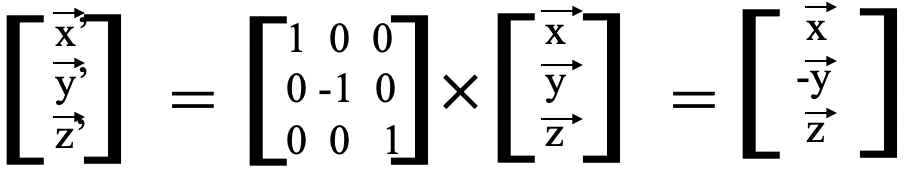
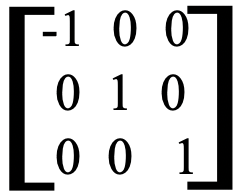
Podemos aplicar el mismo proceso para la operación de simetría σ (yz). El plano espejo σ (yz) contiene las coordenadas y y z, y por lo tanto sus vectores no cambian al aplicar la operación de simetría. Sin embargo, el vector cambia su dirección al reflexionar en el plano yz, y así el signo algebraico de la coordenada x cambia (Fig. 2.3.12).

Figura 2.3.12 Transformación de las coordenadas en H ₂ O tras la aplicación de la operación de simetría σ _yz

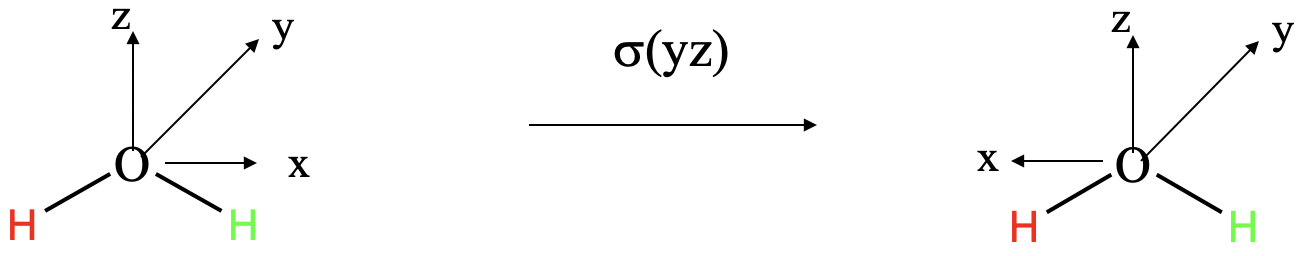
La matriz para las nuevas coordenadas es así -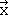,,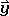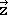. En este caso la matriz que al multiplicarse por la matriz de las coordenadas antiguas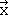,,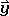 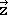da la matriz con las nuevas coordenadas -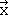,,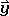 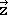tiene la forma a continuación (Fig. 2.3.13).

Figura 2.3.13 operación de simetría σ _yz en H ₂ O en forma de matriz

Podríamos utilizar nuevamente las reglas de multiplicación para matrices para mostrar que la matriz anterior es la representación matricial correcta de la operación de simetría σ (yz), Fig. 2.3.14.

Figura 2.3.14 La multiplicación de la operación σ _yz en forma de matriz con las coordenadas de H ₂ O produce las nuevas coordenadas para H ₂ O

Figura 2.3.15 Transformación de las coordenadas de H ₂ O mediante la operación de simetría E

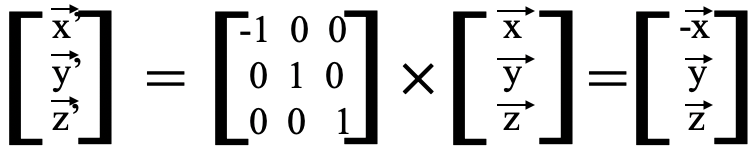
Por último, también podemos determinar la representación matricial de la operación de identidad (Fig. 2.3.15). Tiene la siguiente forma (Fig. 2.3.16).

Figura 2.3.16 Operación de simetría E en H ₂ O en forma de matriz

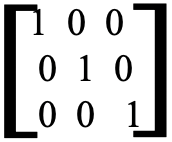
Como antes, podríamos usar las reglas de multiplicación para mostrar que esta matriz produce la matriz correcta para las nuevas coordenadas. Dado que la identidad no le hace nada a un objeto (Fig. 2.3.15), las nuevas coordenadas son las mismas que las coordenadas antiguas (Fig. 2.3.17).

Figura 2.3.17 La multiplicación de la operación de simetría E para H ₂ O con las coordenadas de H ₂ O produce las coordenadas correctas y nuevas para H ₂ O

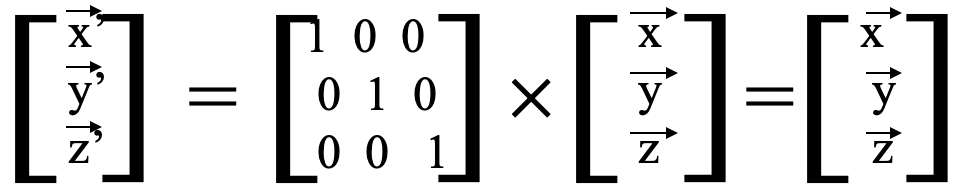
Representaciones reducibles e irreducibles

Veamos más de cerca las cuatro matrices que acabamos de derivar (Fig. 2.3.18).

Figura 2.3.18 Las cuatro matrices para las operaciones de simetría en el grupo de puntos C _2v

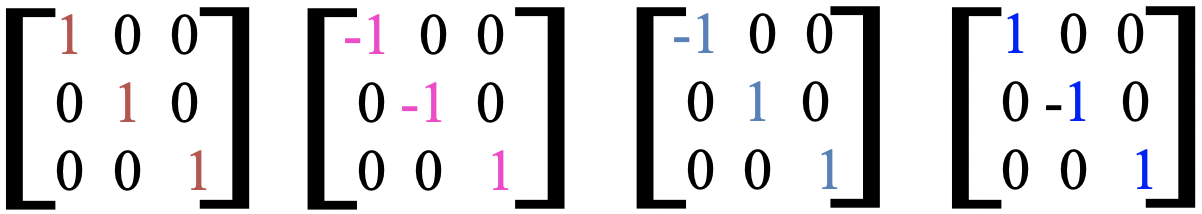
Es de destacar que todos los caracteres son cero, excepto los de una diagonal que va desde la esquina superior izquierda en la matriz hasta la esquina inferior derecha. Esta diagonal se llama la traza de la matriz. Con buena justificación podemos decir que los personajes en el rastro de la matriz nos dicen qué hace la operación de simetría con una coordenada. Si es un -1 el signo algebraico de la coordenada cambia, si es +1, no lo hace. Si escribimos los caracteres de la traza de las matrices que pertenecen a una coordenada específica en una línea debajo de las operaciones de simetría, obtenemos lo que se llama una representación irreducible para la coordenada específica (Fig. 2.3.19).

Figura 2.3.19 Las representaciones irreducibles y reducibles se asocia con las coordenadas en H ₂ O

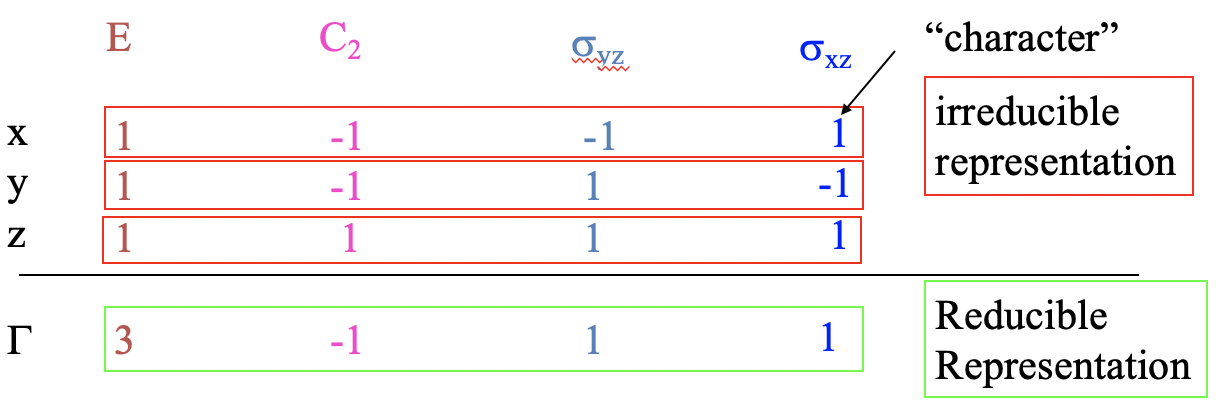
Por ejemplo, para la coordenada x los caracteres de las trazas de las matrices para las operaciones de simetría E, C ₂, σ _yz, σ _xz, son 1, -1, -1 y 1, respectivamente. Para la coordenada y los caracteres serían 1, -1, 1 y -1, y para la coordenada z- son 1, 1, 1 y 1. El uso de una representación irreducible es que nos dice directamente de forma concisa qué hacen las operaciones de simetría a una coordenada específica. La suma de dos o más representaciones irreducibles es una llamada representación reducible. Si resumimos las tres representaciones irreducibles de la Fig. 2.3.19, entonces esto da una representación reducible con los caracteres 1+1+1=3, (-1) + (-1) +1=-1, (-1) +1+1=1, y 1+ (-1) +1=1. Veremos sobre el uso de representaciones reducibles en un poquito.

Tipos de simetría de representaciones irreducibles

Los caracteres específicos en una representación irreducible determinan el tipo de simetría de la representación irreducible. Se denota con una letra mayúscula con subíndices y/o superíndices. Por ejemplo, la representación irreducible para la coordenada x es del tipo B ₁ (Fig. 2.3.20)

Figura 2.3.20 Tipos de simetría de las representaciones irreducibles asociadas a las coordenadas de H ₂ O

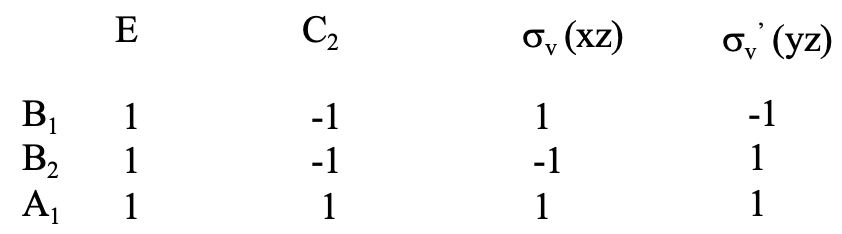
B significa que la simetría es antisimétrica con respecto al eje principal (Fig. 2.3.21).

Figura 2.3.21 La definición de la representación irreducible B

Antisimétrico significa que el signo algebraico de la coordenada cambia a medida que giramos. En este caso el eje principal es el eje C ₂. Podemos ver que el signo algebraico cambia porque el carácter de la representación irreducible para la coordenada x debajo de C ₂ es -1. El subíndice 1 significa que la representación es simétrica a un C ₂ perpendicular al eje principal, o si falta a una vertical σ _v (Figura 2.3.22)

Figura 2.3.22 La definición del subíndice 1 en una representación irreducible

En este caso, no tenemos un C ₂ perpendicular al C ₂ que es nuestro eje principal, pero tenemos dos planos de espejo verticales. Simétrico significa que la coordenada no cambia su signo algebraico ya que se lleva a cabo la operación de simetría. Podemos ver que esto es cierto para la reflexión con el menor número de primos que viene primero en nuestras consideraciones. Se indica con el carácter +1 debajo de la operación de simetría.

La representación irreducible de la coordenada y tiene el tipo de simetría B ₂ (Fig.2.3.20) El tipo de simetría es nuevamente B, porque el carácter debajo de C ₂ es -1. El subíndice es 2 en este caso, y esto significa que la representación es antisimétrica a un C ₂ perpendicular al eje principal o, si falta a un plano vertical σ _v (Fig. 2.3.23)

Figura 2.3.23 La definición del subíndice 2 en la representación irreducible

Podemos ver que el σ _v (xz) es antisimétrico como lo indica el carácter -1 en la representación irreducible. Por último, veamos el tipo de simetría de la representación irreducible para la coordenada z que es _A1 (Fig. 2.3.20) A significa simétrica con respecto a la rotación alrededor del eje principal (Fig. 2.3.24).

Figura 2.3.24 La definición de la representación irreducible A

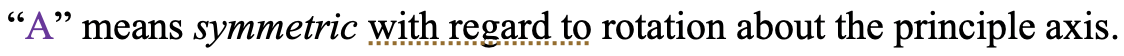
Podemos confirmar la situación simétrica para la rotación alrededor de z verificando que el carácter debajo del eje principal _C2 es +1.

Tipos de simetría de orbitales

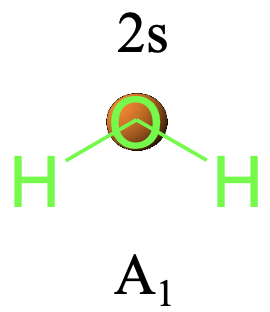
Las representaciones irreducibles son más poderosas que solo decirle el tipo de simetría de una coordenada específica en un grupo de puntos. De manera más general, pueden decir el tipo de simetría de una función matemática en un grupo de puntos específico. Recuerde, que los orbitales son matemáticamente funciones de onda. Por lo tanto, debería ser posible asignar orbitales a un tipo de simetría dentro de un grupo de puntos dado. Veamos por ejemplo, los orbitales 2s y 2p del átomo de oxígeno en la molécula de agua. Consideremos primero el orbital 2s y determinemos qué hacen las operaciones de simetría con él. Podemos ver que ninguna operación de simetría cambia el orbital 2s de ninguna manera, así todos los caracteres de la representación irreducible que pertenece al orbital deben ser +1. Podemos ver que este es sólo el caso de la representación irreducible con la simetría tipo A ₁. Por lo tanto podemos decir que el orbital 2s del O-átomo en la molécula de agua tiene la simetría tipo A ₁ (Fig. 2.3.25).

Figura 2.3.25 El orbital 2s del átomo O en la molécula de agua tiene la simetría tipo A ₁

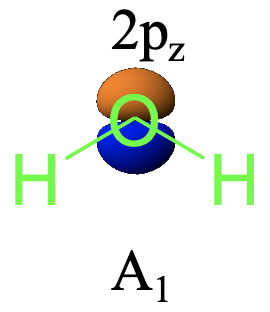
A continuación, determinemos el tipo de simetría del orbital 2p _z. El orbital 2p _z está orientado a lo largo del eje z alrededor del cual giramos. Al llevar una operación C ₂ podemos ver que esta operación no realiza ningún cambio en la órbita. Lo mismo ocurre con las dos operaciones de reflexión. Nuevamente, podemos ver que las operaciones de simetría no cambian el orbital 2p _z de ninguna manera, y por lo tanto también debe pertenecer al tipo de simetría _A1 (Fig. 2.3.26)

Figura 2.3.26 El orbital 2p _z del átomo O en la molécula de agua tiene la simetría tipo A ₁

Sin embargo, para el orbital 2p _x la situación es diferente (Fig. 2.3.27). Podemos ver que girar alrededor del eje C ₂ cambia el signo algebraico de la órbita. Esto significa que el orbital 2p _x debe pertenecer a un tipo de simetría que tiene un carácter de -1 para la operación C ₂. Podemos ver que este puede ser el tipo de simetría B ₁ o B ₂, pero no A ₁. Esto descarta el tipo de simetría _A1. Aún tenemos que decidir si el tipo de simetría es B ₁ o B ₂. Para B ₁ la reflexión en el plano del espejo σ _v (xz) tendría que ser simétrica, y para B ₂ tendría que ser antisimétrica. Podemos ver que el orbital no cambia cuando realizamos la reflexión σ _v (xz), y así el tipo de simetría debe ser B ₁.

Figura 2.3.27 El orbital 2p _x del átomo O en la molécula de agua que tiene la simetría tipo B ₁

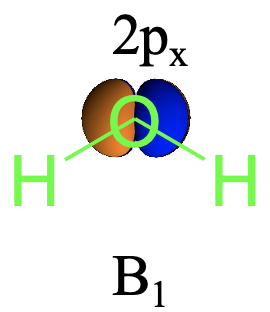
Por último, determinemos el tipo de simetría del orbital 2p _y (Fig. 2.3.28). El orbital 2p _y está orientado perpendicular al plano de papel, el lóbulo azul apunta hacia el frente y el naranja, apenas visible apunta hacia atrás. Podemos ver que cuando giramos alrededor de 180° el lóbulo naranja apunta hacia el frente, y el azul apunta hacia atrás. Eso significa que la función de onda de la órbita ha cambiado su signo algebraico. Por lo tanto, debe ser de tipo simetría B. ¿Cuál es? B ₁ o B ₂? Podemos ver que en este caso el σ _v (xz) sí cambia el signo algebraico de la función de onda porque el lóbulo frontal del orbital se refleja hacia atrás, y el lóbulo en la parte posterior se refleja hacia el frente. Así, es antisimétrico con respecto a σ _v (xz) y así debe pertenecer a la simetría tipo B ₂.

Figura 2.3.28 El orbital 2p _y del átomo O en la molécula de agua que tiene la simetría tipo B ₂

Podríamos haber determinado los tipos de simetría de los orbitales también desde una perspectiva más matemática. Recuerde que cuando discutimos los orbitales atómicos vimos que la función de onda de un orbital p _z es una función lineal de la coordenada z (Fig. 2.3.29). Por lo tanto, tiene el mismo tipo de simetría que la coordenada z, es decir, A ₁. Un orbital p _y es una función lineal de y, por lo tanto, tiene el mismo tipo de simetría que la coordenada y: B ₂. Un orbital p _x es sólo una función de x, por lo tanto su tipo de simetría es el de la coordenada x: B ₁. El orbital 2s no es una función de ninguna coordenada. Por eso debe pertenecer al tipo de simetría en el que todos los caracteres son +1 que es el tipo de simetría _A1 en el grupo de puntos C _2v.

Figura 2.3.29 Las funciones de onda angular de los orbitales 2s y 2p en coordenadas cartesianas.

Por los mismos medios también podemos determinar el tipo de simetría de los d orbitales del átomo O en H ₂ O. No están ocupados, y no involucrados en la unión, pero sin embargo son posibles estados para los electrones. Determinémoslos usando la siguiente tabla (Fig. 2.3.30)

Figura 2.3.30 Tabla de caracteres para el grupo de puntos C _2v

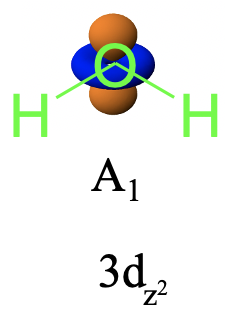
¿El 3d _{z ²} — orbital cambia cuando se realizan las operaciones de simetría (Fig. 2.3.31)? ¡No, no lo hace! Por lo tanto, tiene la simetría tipo A ₁.

Figura 2.3.31 El orbital 3d _{z ²} del átomo de O de la molécula de agua tiene la simetría tipo A ₁

¿Qué pasa con el 3d _xz? El orbital 3d _xz cambia su signo algebraico cuando se realiza la operación C ₂, pero no cuando se realizan las reflexiones. Por lo tanto, es de tipo simetría B ₁ (Fig. 2.3.32).

Figura 2.3.32 El orbital 3d _xz del átomo de O de la molécula de agua tiene la simetría tipo B ₁

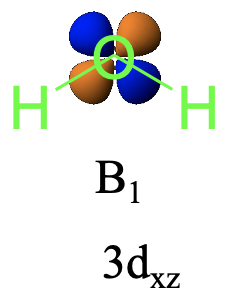
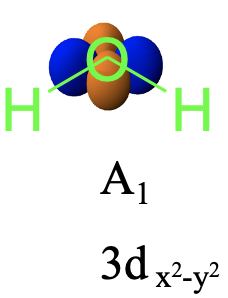
El 3d _{x ² - y ²} -orbital tampoco cambia cuando se ejecutan las operaciones de simetría, por lo que es de simetría tipo A ₁ (Fig. 2.3.33)

Figura 2.3.33 El orbital 3d _{x ² - y ²} del átomo de O de la molécula de agua tiene la simetría tipo A ₁

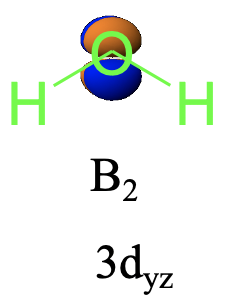
Para la rotación orbital d _yz y la reflexión σ _v (xz) cambia el signo algebraico, por lo tanto es B ₂ (Fig. 2.3.24).

Figura 2.3.34 El orbital 3d _yz del átomo O de la molécula de agua tiene la simetría tipo B ₂

Para el _xy 3d podemos ver que la rotación no cambia el orbital, sino que la reflexión σ _v (xz) sí. Esto significa que el tipo de simetría debe ser A ₂ (Fig. 2.3.35).

Figura 2.3.35 El orbital _xy 3d del átomo de O de la molécula de agua tiene la simetría tipo A ₂

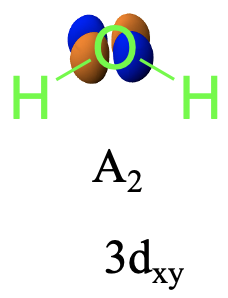
Se trata de un nuevo tipo de simetría que también pertenece al grupo de puntos C _2v. Ninguna coordenada única es de este tipo de simetría, sino funciones matemáticas que son producto de las coordenadas x e y, como el orbital 3d _xy son. Del mismo modo, debido a que el orbital 3d _{z ²} es una función de z ² y el 3d _{z ²} tiene el tipo de simetría _A1 cualquier función de z ² tiene este tipo de simetría. Análogamente, cualquier función que sea el producto de la coordenada x y z pertenece al tipo de simetría B ₁, cualquier función que sea una función de x ^{2 -y 2} pertenece al tipo de simetría _A1, y cualquier función que sea un producto de y y z pertenece al simetría tipo B _2.

Tablas de caracteres

Solo hay un número finito de representaciones irreducibles y tipos de simetría en un grupo de puntos específico.

Generalmente, todas las representaciones irreducibles que son posibles en un grupo puntual específico definen la llamada tabla de caracteres del grupo de puntos Fig. 2.3.36).

Definición: Tabla de caracteres

Un conjunto completo de representaciones irreducibles en un grupo de puntos define su tabla de caracteres

Las tablas de caracteres describen lo que hacen las operaciones de simetría de un grupo de puntos con una función matemática. Se puede ver la tabla completa de caracteres del grupo de puntos C _2v a continuación (Fig. 2.3.36).

Figura 2.3.36 Tabla de caracteres para el grupo de puntos C _2v

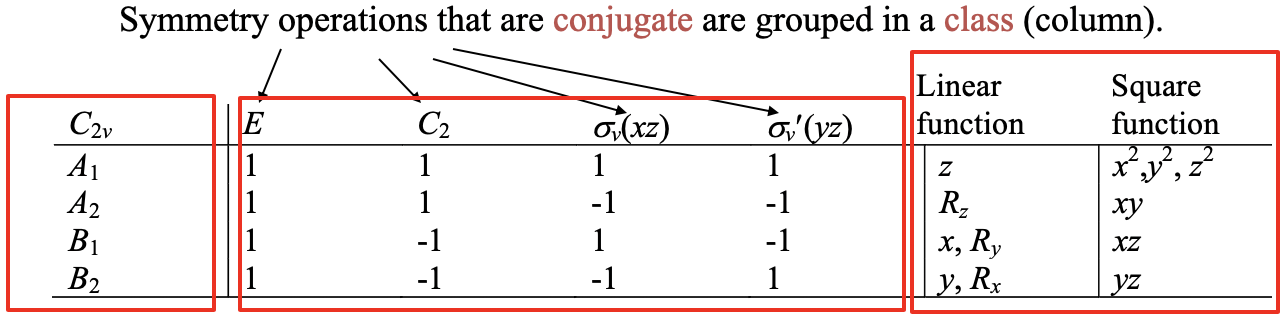
Está hecho de varias filas y columnas. En la primera columna puede encontrar el símbolo de grupo de puntos a la izquierda, y luego los símbolos para los diferentes tipos de simetría de las representaciones irreducibles que tiene el grupo de puntos. Después, hay varias columnas con operaciones de simetría en la primera fila, y los caracteres para las representaciones irreducibles a continuación. Cada una de estas columnas se llama clase. Las operaciones de simetría que son conjugadas se agrupan en la misma columna, o en la misma clase. Para el grupo puntual C _2v, cada operación obtiene su propia columna y eso significa que todas son no conjugadas. Pero esto no siempre es cierto, en muchos otros grupos de puntos hay varias operaciones de simetría que son conjugadas, y listadas en la misma columna. Ya hemos discutido cualitativamente que las operaciones conjugadas transforman las coordenadas de un objeto de manera similar. Ahora tenemos una definición más exacta que es que siempre que los personajes para las operaciones en sus representaciones irreducibles son iguales, pertenecen a la misma clase.

Figura 2.3.37 Transformación de un vector rotacional que gira alrededor de z mediante las operaciones de simetría en el grupo de puntos C _2v

La suma de caracteres debajo de la operación de identidad E define la dimensión del grupo de puntos. Para C _2v la dimensión del grupo de puntos es 1+1+1+1=4. El orden (h) del grupo de puntos es solo la suma de todas las operaciones de simetría en el grupo de puntos. Para C _2v el pedido es 4. En las dos columnas del extremo derecho de la tabla de caracteres se pueden encontrar las funciones matemáticas que pertenecen a las diferentes representaciones irreducibles. En la segunda columna de la derecha se listan las funciones lineales y rotacionales, y en la columna extrema derecha se listan las funciones cuadradas. Por ejemplo, la letra z está en la fila asociada con el tipo de simetría _A1. Esto significa que cualquier función lineal de la coordenada z tiene el tipo de simetría _A1. Las letras x e y están en filas para el tipo de simetría B ₁ y B ₂ respectivamente. Esto significa que cualquier función lineal de x e y tiene la simetría tipo B ₁ y _B2 respectivamente.

También puede ver los símbolos R _z, R _x y R _y en la misma columna. Estos símbolos representan funciones rotacionales alrededor del eje z, x e y respectivamente. R _z está en la fila del tipo de simetría _A2, lo que significa que cualquier función rotacional de z tiene el tipo de simetría _A2. ¿Cómo podemos entender eso? Considera un vector rotacional alrededor de z que indica rotación en sentido horario (Fig. 2.3.37). Si giramos este vector 180° en sentido antihorario no cambiará su dirección, seguirá apuntando en sentido horario, y así el carácter debajo de C ₂ en la tabla de caracteres debería ser un 1. Esto descarta que la simetría sea de tipo B, debe ser de tipo A ₁ o A ₂. Podemos ver además que cuando reflejamos este vector en los dos planos especulares verticales, invierte su dirección, apuntando ahora en sentido contrario a las agujas del reloj. Por lo tanto, los caracteres debajo de los dos planos espejo deben ser ambos -1. Esto significa que el tipo de simetría debe ser A ₂. Si hiciéramos el mismo ejercicio con los vectores rotacionales R _{x y R y} podríamos demostrar que pertenecen a los tipos de simetría B ₂ y B ₁ respectivamente. En la última columna se listan las funciones cuadradas. La fila en la que se encuentra la función te da la información sobre el tipo de simetría de la función cuadrada. Por ejemplo, cualquier función de x ², y ², o z ² tiene el tipo de simetría _A1, una función que es un producto de x e y tiene el tipo de simetría _A2 y así sucesivamente.

Representaciones Matriciales de Operaciones de Simetría en C _3v

Ahora pasemos del grupo de puntos C _2v al grupo de puntos C _3v y determinemos las representaciones matriciales de las operaciones de simetría. Veremos que para esto, y más generalmente para cualquier grupo de puntos con ejes rotacionales con un orden superior a 2, es posible una degeneración de simetría, lo que significa que dos o incluso las tres coordenadas pertenecen al mismo tipo de simetría. Las coordenadas no cambian independientemente a la ejecución de una operación de simetría, están vinculadas entre sí. Veamos la molécula de amoníaco que pertenece al grupo puntual C _3v.

Figura 2.3.38 Una representación adecuada del sistema de coordenadas en la molécula de amoníaco perteneciente al grupo puntual C _3v

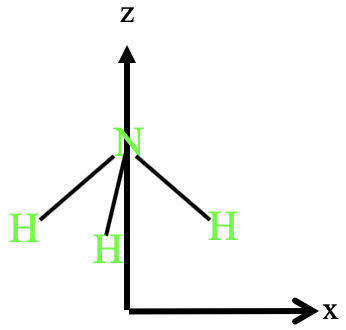
Podemos definir el sistema de coordenadas para que el eje x apunte a la derecha, el eje z apunte a la parte superior, y el eje y quede perpendicular al plano del papel (Fig. 2.3.38). La molécula de amoníaco está orientada de manera que su pirámide apunta hacia la dirección z, y uno de los tres enlaces N-H está dentro del plano xz.

Ahora veamos cómo cambian las coordenadas cuando giramos la molécula por un ángulo general arbitrario θ alrededor del eje z. En el diagrama que se muestra a continuación, ahora miramos a lo largo del eje z, y el plano xy está dentro del plano de papel (Fig. 2.3.39).

Figura 2.3.39 Transformación de las coordenadas x e y por rotación de la molécula de amoníaco alrededor de un ángulo arbitrario θ

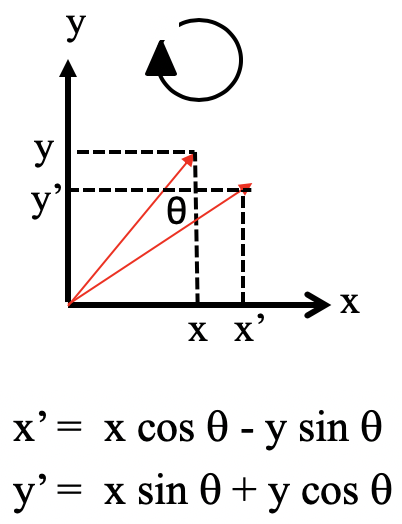
Podemos ver que la rotación cambia juntas tanto la coordenada x como la y, pero deja la coordenada z inalterada. Según la trigonometría la nueva coordenada x x' es x' = x cos θ - y sin θ. La nueva coordenada y' es y' = x sin θ + y cos θ.

La representación matricial de una operación de simetría que gira alrededor de un ángulo arbitrario debe ser capaz de convertir las coordenadas antiguas x, y, z en las nuevas coordenadas a continuación (Fig. 2.3.40).

Figura 2.3.40 Las nuevas coordenadas (forma de matriz) de la molécula NH ₃ después de la rotación alrededor de un ángulo arbitrario θ

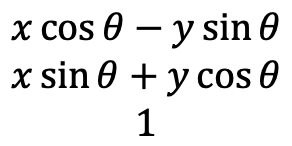
La matriz que es capaz de hacer esto tiene la siguiente forma (Fig. 2.3.41)

Figura 2.3.41 Representación de matriz para la operación de rotación alrededor de un ángulo arbitrario θ

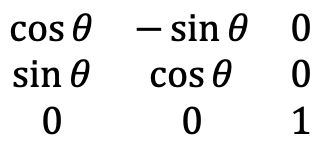
Podríamos utilizar nuevamente las reglas de multiplicación para las matrices para mostrar que esta matriz es la matriz correcta.

La matriz que acabamos de desarrollar gira alrededor de un ángulo general θ. ¿Cómo se ve esta matriz en el grupo de puntos C _3v donde giramos alrededor de 120° y 240°? Bueno, todo lo que tenemos que hacer es insertar los valores de 120° y 240° para θ en la matriz. El seno de 120° es -√3/2, y el seno de 240° es √3/2. El coseno de 120° y 240° son ambos -1/2 (Fig. 2.3.42).

Figura 2.3.42 Los valores de seno y coseno para una rotación de 120° y 240° en el sentido de las agujas del reloj

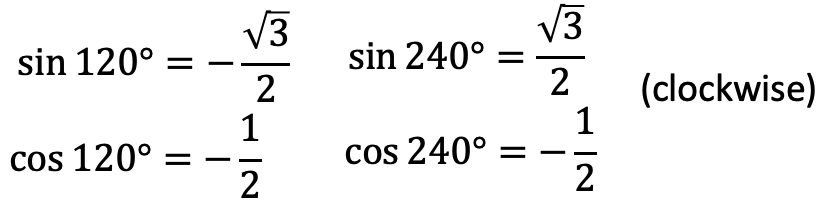
Tenga en cuenta que estos son los valores para la rotación en sentido horario. Debido a que las operaciones C ₃ giran en sentido contrario a las agujas del reloj, debemos usar los valores para la rotación de 240° para el C ₃ ¹ y los valores para la rotación de 120° para la operación C ₃ ². Considerando esto, la matriz para la operación C ₃ ² y la matriz para la operación C ₃ ¹ son las matrices que se muestran a continuación (Fig. 2.3.43).

Figura 2.3.43 Las matrices para la operación C ₃ ² y la operación C ₃ ¹

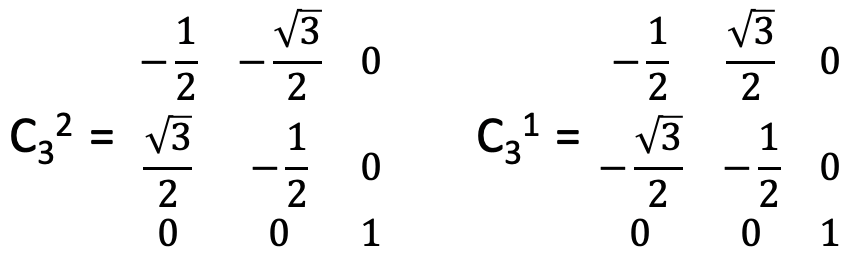
Podemos ver que hay una diferencia significativa en todas las matrices que vimos antes. Hay caracteres distintos de cero no sólo en la traza de la matriz, sino también en otras posiciones dentro de la matriz, en particular en las dos primeras filas que representan las coordenadas x e y. Esto es consecuencia de que las coordenadas x e y ya no son independientes en C _3v, cambian de manera dependiente. Nosotros decimos que son degenerados.

Ahora podemos determinar las operaciones de simetría restantes en C _3v. Hay tres planos de espejo verticales conjugados a considerar. El primer plano espejo se encuentra dentro del plano xz y pasa a través del enlace N-H que está dentro del plano xz. La matriz para ello es simple. Tiene la siguiente forma (Fig. 2.3.44).

Figura 2.3.44 La matriz para el primer plano de espejo en el grupo de puntos C _3v

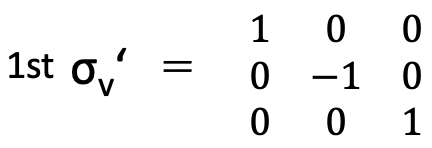
Es sencillo entender por qué la matriz tiene esta forma. Debido a que el plano espejo está en el plano xz las coordenadas x y z no se ven afectadas por la reflexión en este plano. Por lo tanto, hay dos +1 caracteres en la traza de la matriz en las filas para las coordenadas x y z, respectivamente, y todos los demás caracteres en estas filas son 0. El carácter en la segunda fila en la traza de la matriz es -1 porque el signo algebraico de la coordenada y cambia a medida que reflejamos en el plano xz. Sin embargo, los otros dos planos especulares no son coplanares con dos coordenadas cualesquiera, y para estos planos las coordenadas x e y vuelven a depender. A continuación se muestran la matriz para el segundo plano espejo y la matriz para el tercero (Fig. 2.3.45).

Figura 2.3.45 Las matrices para el segundo plano de espejo y la matriz para el tercer plano de espejo en C _3v

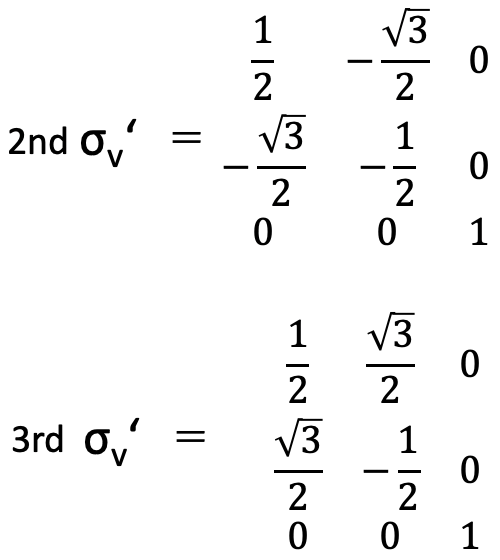
No los vamos a derivar en detalle aquí. Es suficiente para nosotros entender aquí que estas matrices tienen formas más complejas con valores distintos de cero fuera del rastro de la matriz debido a la degeneración de las coordenadas x e y. Por último, no debemos olvidar la identidad. Debido a que la identidad no hace nada con un objeto, su matriz es siempre la matriz de abajo en cualquier grupo de puntos (Fig. 2.3.46).

Figura 2.3.46 La matriz de identidad para cualquier grupo de puntos

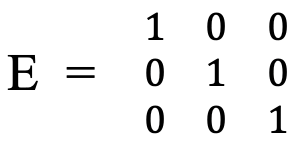
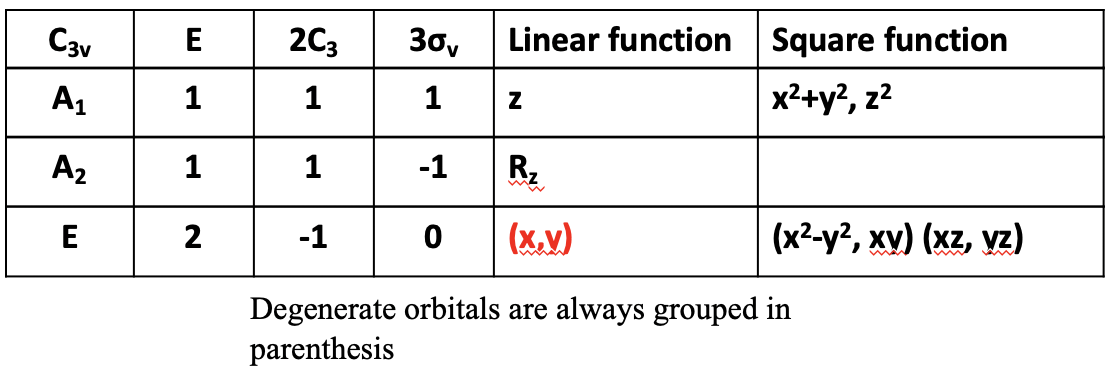
Debido a que conocemos ahora las representaciones matriciales de las operaciones de simetría podemos entender la tabla de caracteres para el grupo de puntos C _3v (Fig. 2.3.47)

Figura 2.3.47 La tabla de caracteres para el grupo de puntos C _3v

La tabla de caracteres tiene tres clases para los tres grupos de operaciones de simetría no conjugadas. En la primera clase sólo existe la identidad. Se puede ver que la segunda clase contiene las operaciones C ₃ ¹ y C ₃ ², resumidas como 2C ₃. La tercera clase contiene las 3 operaciones conjugadas σ _v. En el grupo puntual C _3v hay tres representaciones irreducibles. Los dos primeros tienen los tipos de simetría _A1 y _A2 respectivamente, el tercero de es de tipo E. El último es nuevo para nosotros. Significa “doble degeneración”, y este tipo de simetría existe debido a la doble degeneración de la coordenada x e y. Se puede ver que la tabla de caracteres establece explícitamente que x e y son doblemente degenerados cuando se mira en la última columna de la tabla de caracteres. Las letras x e y están entre paréntesis separadas por una coma. Los paréntesis indican la degeneración de estas dos coordenadas. De manera más general, dos funciones cualesquiera que sean funciones lineales de x o y son degeneradas en C _3v. Se puede ver que también hay otras funciones que son degeneradas. Por ejemplo, las funciones de x ² -y ² y xy son degeneradas. También las funciones de xz e yz son degeneradas.

Se puede ver que los caracteres en la representación irreproducible del tipo de simetría E también son inusuales. Anteriormente, solo nos encontramos con los caracteres 1 y -1. Sin embargo, el carácter debajo de la identidad es 2, y el carácter de la clase para los planos de espejo verticales es 0. ¿Cómo podemos entender a estos personajes? La respuesta tiene que ver con la doble degeneración de las coordenadas x e y. Debido a esta doble degeneración, los caracteres en las representaciones irreducibles son la suma de los caracteres en la traza de las matrices para la coordenada x e y. Verifiquemos cuáles son. Se pueden ver las tres matrices que representan las tres clases de las operaciones de simetría a continuación (Fig. 2.3.48).

Figura 2.3.48 Las tres matrices que representan las tres clases de operaciones de simetría

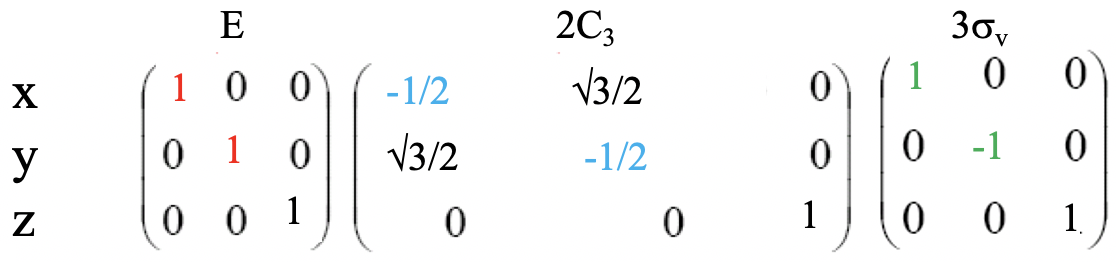
Para la identidad la suma de los dos caracteres es 1+1=2 lo que explica el carácter 2 en la representación irreducible E. Para la matriz que representa las operaciones C ₃ los caracteres en la traza de la matriz para x e y son -1/2. Cuando se resume -1/2 + (-1/2) da -1 lo que explica el carácter -1 en la representación irreducible. Por último, para la matriz que representa los planos especulares verticales los caracteres en la traza de la matriz para las coordenadas x e y son 1 y -1, respectivamente. -1+1=0 lo que explica el carácter 0 en la representación irreducible del tipo de simetría E.

La coordenada z tiene el tipo de simetría _A1 que es sencillo de entender porque los caracteres para z en la traza de las matrices para las tres clases diferentes de operaciones de simetría son todos 1. También se puede ver en la tabla de caracteres que nuevamente hay una representación irreducible a la que no pertenece ninguna coordenada. Es el que tiene la simetría tipo A ₂. En C _3v solo las funciones rotacionales alrededor de z tienen ese tipo de simetría.

Tipos de simetría de representaciones irreducibles degeneradas

No solo hay representaciones irreducibles doblemente degeneradas, denotadas por un símbolo E, también pueden haber tres degeneradas, indicadas por un símbolo T. En este caso las tres coordenadas x, y, y z son degeneradas. La triple degeneración no aparece en el grupo puntual C _3v, sino en otros grupos puntuales, en particular los grupos puntuales de alta simetría (Fig. 2.3.49).

Figura 2.3.49 La definición de representaciones irreducibles “E” y “D”

Tanto los símbolos E como T pueden llevar subíndices y primos que tienen significados específicos. El prime (') y (“) double prime en la etiqueta de representación de simetría indica “simétrico” o “antisimétrico” con respecto a σ _h, por ejemplo E` o E`` (Fig. 2.3.50).

Figura 2.3.50 La definición de prime (') y (“) en representaciones irreducibles

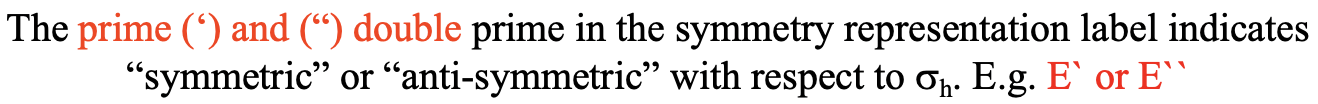
Los subíndices g y u representan las palabras alemanas “gerade” y “ungerade” y a g y a u indican “simétrico” o “antisimétrico” con respecto a la inversión, i, respectivamente (Fig. 2.3.51).

Figura 2.3.51 La definición de g (gerade) y u (ungerada) en representaciones irreducibles

Por ejemplo, puede haber tipos de simetría como T _g o E _u. Hay otros subíndices posibles, y no necesitamos atravesarlos exhaustivamente. Basta con entender que indican una cierta propiedad de simetría en un tipo de simetría.

Tablas de caracteres y orbitales degenerados

Una de las propiedades más útiles de las tablas de caracteres es que se pueden identificar orbitales degenerados muy fácilmente. Por ejemplo, una mirada rápida a la tabla de caracteres del grupo de puntos C _3v revela que los orbitales 2p _x y 2p _y en NH ₃ deben estar degenerados (Fig. 2.3.52).

Figura 2.3.52 Tabla de caracteres del grupo de puntos C _3v

Esto se debe a que el orbital 2p _x es una función lineal de x, y el orbital 2p _y es una función lineal de y, y las funciones lineales de x e y se enumeran entre paréntesis en la representación irreducible doblemente degenerada del tipo E. Esta doble degeneración también podría derivarse por inspeccionar los orbitales en la molécula NH ₃, pero esto no es tan fácil como buscar la tabla de caracteres. Se pueden ver los orbitales 2p _x y 2p _y en la molécula de amoníaco a continuación (Fig. 2.3.53).

Figura 2.3.53 Los orbitales 2p _{x y 2p y} en amoníaco

Los dos orbitales se encuentran perpendiculares entre sí, pero la molécula NH ₃ tiene simetría rotacional C ₃. Por lo tanto, ¿por qué los dos orbitales serían degenerados en simetría? Si son degenerados, entonces debe haber al menos una operación de simetría que pueda interconvertir los dos orbitales. De la representación anterior no es obvio qué operación de simetría podría ser esta.

Identificando la Doble Degeneración de 2p _x y 2p _y en NH ₃

Podemos hacer un pequeño truco para ver que una operación de reflexión es la que puede interconvertir los dos orbitales. El truco es rotar 45° el sistema de coordenadas. Se puede ver la molécula de amoníaco en la perspectiva del ave a continuación (Fig. 2.3.54).

Figura 2.3.54 Amoníaco en la perspectiva del ave con una flecha que indica el plano de reflexión que interconvierte 2p _x y 2p _y

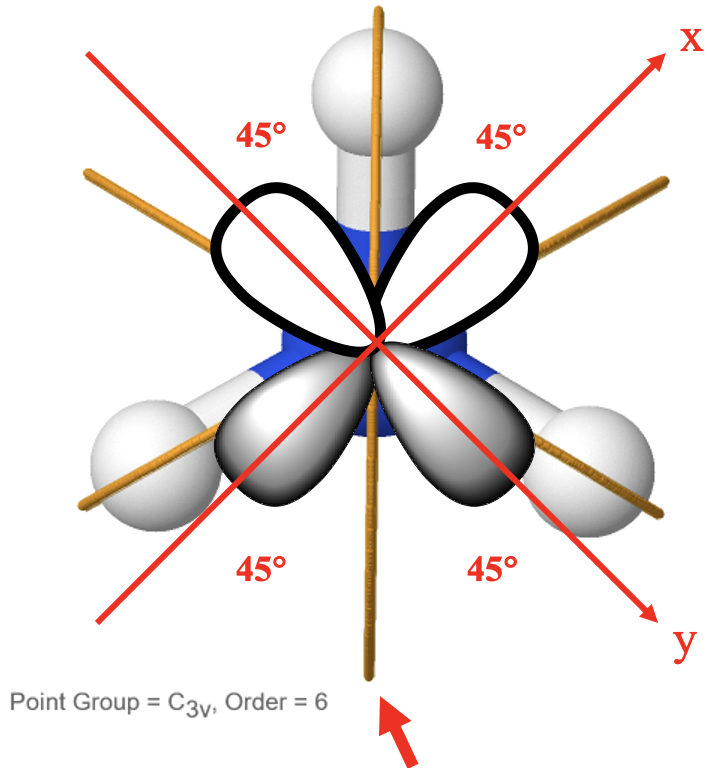
Esto significa que miramos perpendiculares a la base de la pirámide. Se puede ver la molécula NH ₃ con sus tres planos espejo arriba. Ahora podemos elegir nuestro sistema de coordenadas para que los ejes x e y se roten 45° con respecto a uno de los planos espejo. Por definición, el orbital 2p _x debe estar orientado a lo largo del eje x, y el orbital 2p _y debe estar orientado a lo largo del eje y. Se puede ver que uno de los planos espejo, a saber, el que se orienta verticalmente, es capaz de interconvertir los dos orbitales. Al reflexionar, los lóbulos izquierdo y derecho de ambos orbitales intercambiarán sus posiciones, de manera que una vez completada la operación de simetría, se interconvierten los orbitales 2p. En general podemos ver que probar la degeneración de dos orbitales por inspección puede ser complicado. Un rápido vistazo a la tabla de caracteres puede decirnos mucho más fácilmente si dos orbitales están degenerados.

---

Template:ContribLandskron