1.6: Estructura y Unión - Estructura Cristalina
- Page ID
- 69544
Introducción
En cualquier tipo de discusión sobre materiales cristalinos, es útil comenzar con una discusión de cristalografía: el estudio de la formación, estructura y propiedades de los cristales. Una estructura cristalina se define como la disposición repetitiva particular de átomos (moléculas o iones) a lo largo de un cristal. La estructura se refiere a la disposición interna de las partículas y no a la apariencia externa del cristal. Sin embargo, estos no son del todo independientes ya que la apariencia externa de un cristal suele estar relacionada con la disposición interna. Por ejemplo, los cristales de sal de roca cúbica (NaCl) son físicamente cúbicos en apariencia. Solo algunas de las posibles estructuras cristalinas son motivo de preocupación con respecto a las sales inorgánicas simples y éstas serán discutidas en detalle, sin embargo, es importante entender la nomenclatura de la cristalografía.
Cristalografía
Celosía Bravais
La celosía Bravais es el bloque básico de construcción a partir del cual se pueden construir todos los cristales. El concepto se originó como un problema topológico de encontrar el número de diferentes formas de organizar puntos en el espacio donde cada punto tendría una atmósfera idéntica. Es decir, cada punto estaría rodeado por un conjunto idéntico de puntos que cualquier otro punto, de manera que todos los puntos serían indistinguibles entre sí. El matemático Auguste Bravais descubrió que había 14 colecciones diferentes de los grupos de puntos, que se conocen como celosías de Bravais. Estas celosías se dividen en siete “sistemas cristalinos diferentes, diferenciados por la relación entre los ángulos entre los lados de la celda unitaria y la distancia entre puntos en la celda unitaria. La celda unitaria es el grupo más pequeño de átomos, iones o moléculas que, cuando se repiten a intervalos regulares en tres dimensiones, producirán la red de un sistema cristalino. El parámetro de celosía es la longitud entre dos puntos en las esquinas de una celda unitaria. Cada uno de los diversos parámetros de celosía se designan con las letras a, b y c. Si dos lados son iguales, como en una celosía tetragonal, entonces las longitudes de los dos parámetros de celosía se designan a y c, omitiéndose b. Los ángulos son designados por las letras griegas α, β y γ, de tal manera que un ángulo con una letra griega específica no es subtendido por el eje con su equivalente romano. Por ejemplo, α es el ángulo incluido entre los ejes b y c.
El cuadro\(\PageIndex{1}\) .8 muestra los diversos sistemas cristalinos, mientras que en la Figura\(\PageIndex{1}\) .16 se muestran las 14 celosías de Bravais. Es importante distinguir las características de cada uno de los sistemas individuales. En la Tabla\(\PageIndex{1}\) .9 se muestra un ejemplo de un material que toma cada una de las celosías de Bravais.
| Sistema | Longitudes y ángulos axiales | Geometría de celda unitaria |
| cúbico | a = b = c, α = β = γ= 90 ◦ | 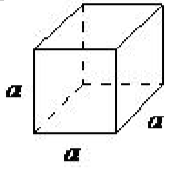 |
| tetragonal | a = b ≠ c, α = β = γ= 90 ◦ | 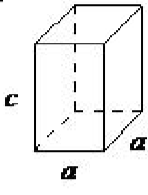 |
| ortorrómbico | a ≠ b ≠ c, α = β = γ= 90 ◦ | 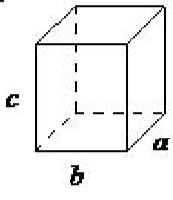 |
| romboédrico | a = b = c, α = β = γ ≠ 90 ◦ | 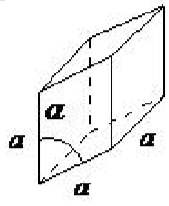 |
| hexagonal | a = b ≠ c, α = β = 90 ◦, γ = 120 ◦ | 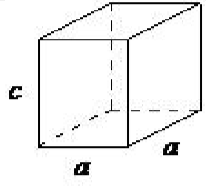 |
| monoclínico | a ≠ b ≠ c, α = γ = 90 ◦, β ≠ 90 ◦ | 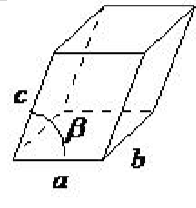 |
| triclínica | a ≠ b ≠ c, α ≠ β ≠ γ | 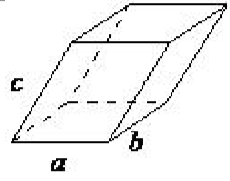 |
| Sistema de cristal | Ejemplo |
| triclínica | K 2 S 2 O 8 |
| monoclínico | Como 4 S 4, KNO 2 |
| romboédrico | Hg, Sb |
| hexagonal | Zn, Co, NIs |
| ortorrómbico | Ga, Fe 3 C |
| tetragonal | En, TiO 2 |
| cúbico | Au, Si, NaCl |
La celosía cúbica es el más simétrico de los sistemas. Todos los ángulos son iguales a 90 ◦, y todos los lados son de la misma longitud (a = b = c). Solo se requiere la longitud de uno de los lados (a) para describir completamente este sistema. Además del cúbico simple, la celosía cúbica también incluye cúbico centrado en el cuerpo y cúbico centrado en la cara (Figura\(\PageIndex{1}\) .16). El cúbico centrado en el cuerpo resulta de la presencia de un átomo (o ion) en el centro de un cubo, además de los átomos (iones) posicionados en los vértices del cubo. De manera similar, un cúbico centrado en la cara requiere, además de los átomos (iones) posicionados en los vértices del cubo, la presencia de átomos (iones) en el centro de cada una de las caras de los cubos.
La celosía tetragonal tiene todos sus ángulos iguales a 90 ◦, y tiene dos de los tres lados de igual longitud (a = b). El sistema también incluye tetragonal centrado en el cuerpo (Figura\(\PageIndex{1}\) .16).
En una celosía ortorrómbica todos los ángulos son iguales a 90 ◦, mientras que todos sus lados son de longitud desigual. El sistema solo necesita ser descrito por tres parámetros de celosía. Este sistema también incluye ortorrómbico centrado en el cuerpo, ortorrómbico centrado en la base y ortorrómbico centrado en la cara (Figura\(\PageIndex{1}\) .16). Una red centrada en la base tiene, además de los átomos (iones) posicionados en los vértices de la red ortorrómbica, átomos (iones) posicionados en solo dos caras opuestas.
La celosía romboédrica también se conoce como trigonal, y no tiene ángulos iguales a 90 ◦, pero todos los lados son de igual longitud (a = b = c), requiriendo así solo por un parámetro de celosía, y los tres ángulos son iguales (α = β = γ ).
Una estructura cristalina hexagonal tiene dos ángulos iguales a 90 ◦, con el otro ángulo (γ) igual a 120 ◦. Para que esto suceda, los dos lados que rodean el ángulo de 120 ◦ deben ser iguales (a = b), mientras que el tercer lado (c) está a 90 ◦ a los otros lados y puede ser de cualquier longitud.
La celosía monoclínica no tiene lados de igual longitud, pero dos de los ángulos son iguales a 90 ◦, siendo el otro ángulo (generalmente definido como β) algo distinto de 90 ◦. Se trata de un prisma de paralelogramo inclinado con bases rectangulares. Este sistema también incluye monoclínico centrado en la base (Figura\(\PageIndex{1}\) .16).
En la red triclínica ninguno de los lados de la celda unitaria es igual, y ninguno de los ángulos dentro de la celda unitaria es igual a 90 ◦. La red triclínica se elige de tal manera que todos los ángulos internos sean agudos u obtusos. Este sistema cristalino tiene la simetría más baja y debe ser descrito por 3 parámetros de celosía (a, b y c) y los 3 ángulos (α, β y γ).
Posiciones de los átomos, direcciones de los cristales e indicaciones Miller
Posiciones de los átomos y ejes cristalinos
La estructura de un cristal se define con respecto a una celda unitaria. Como todo el cristal consiste en células unitarias repetitivas, esta definición es suficiente para representar todo el cristal. Dentro de la celda unitaria, la disposición atómica se expresa usando coordenadas. Hay dos sistemas de coordenadas comúnmente en uso, lo que puede causar cierta confusión. Ambos usan una esquina de la celda unitaria como origen. El primer sistema menos comúnmente visto es el de coordenadas cartesianas u ortogonales (X, Y, Z). Estos suelen tener las unidades de Angstroms y se relacionan con la distancia en cada dirección entre el origen de la célula y el átomo. Estas coordenadas pueden ser manipuladas de la misma manera que se utilizan con gráficas bidimensionales o tridimensionales. Es muy sencillo, por lo tanto, calcular distancias y ángulos interatómicos dadas las coordenadas cartesianas de los átomos. Desafortunadamente, la naturaleza repetitiva de un cristal no se puede expresar fácilmente usando tales coordenadas. Por ejemplo, considere una celda cúbica de dimensión 3.52 Å. Pretende que esta celda contiene un átomo que tiene las coordenadas (1.5, 2.1, 2.4). Es decir, el átomo está a 1.5 Å de distancia del origen en la dirección x (que coincide con el eje de la célula a), 2.1 Å en el y (que coincide con el eje de la célula b) y 2.4 Å en el z (que coincide con el eje de la célula c). Habrá un átomo equivalente en la siguiente celda unitaria a lo largo de la dirección x, que tendrá las coordenadas (1.5 + 3.52, 2.1, 2.4) o (5.02, 2.1, 2.4). Este fue un cálculo bastante simple, ya que la célula tiene una simetría muy alta y así los ejes celulares, a, b y c, coinciden con los ejes cartesianos, X, Y y Z. Sin embargo, considere células de menor simetría como triclínicas o monoclínicas en las que los ejes celulares no son mutuamente ortogonales. En tales casos, expresar la naturaleza repetitiva del cristal es mucho más difícil de lograr.
En consecuencia, las coordenadas atómicas generalmente se expresan en términos de coordenadas fraccionarias, (x, y, z). Este sistema de coordenadas es coincidente con los ejes celulares (a, b, c) y se relaciona con la posición del átomo en términos de la fracción a lo largo de cada eje. Considerar el átomo en la celda cúbica discusión anterior. El átomo fue de 1.5 Å en la dirección a alejándose del origen. Como el eje a tiene una longitud de 3.52 Å, el átomo está (1.5/3.52) o 0.43 del eje alejado del origen. De igual manera, es (2.1/3.52) o 0.60 del eje b y (2.4/3.5) o 0.68 del eje c. Las coordenadas fraccionarias de este átomo son, por lo tanto, (0.43, 0.60, 0.68). Las coordenadas del átomo equivalente en la siguiente celda sobre la dirección a, sin embargo, se calculan fácilmente ya que este átomo está simplemente a 1 celda unitaria de distancia en a. así, todo lo que uno tiene que hacer es agregar 1 a la coordenada x: (1.43, 0.60, 0.68). Dichas transformaciones se pueden realizar independientemente de la forma de la celda unitaria. Las coordenadas fraccionarias, por lo tanto, se utilizan para retener y manipular la información cristalina.
Direcciones Crystal
La designación de los vectores individuales dentro de cualquier red cristalina dada se logra mediante el uso de multiplicadores de número entero del parámetro de celosía del punto en el que el vector sale de la celda unitaria. El vector se indica mediante la notación [hkl], donde h, k y l son recíprocas del punto en el que el vector sale de la celda unitaria. El origen de todos los vectores se asume definido como [000]. Por ejemplo, la dirección a lo largo del eje a de acuerdo con este esquema sería [100] porque éste tiene un componente solo en la dirección a y ningún componente a lo largo de la dirección axial b o c. Un vector diagonalmente a lo largo de la cara definida por los ejes a y b sería [110], mientras que ir de una esquina de la celda unitaria a la esquina opuesta estaría en la dirección [111]. En la Figura\(\PageIndex{1}\) .17 se muestran algunos ejemplos de las distintas direcciones en la celda unitaria. La notación de dirección del cristal se compone de la combinación más baja de números enteros y representa distancias unitarias en lugar de distancias reales. Una dirección [222] es idéntica a una [111], por lo que se usa [111]. No se utilizan fracciones. Por ejemplo, un vector que intercepta el centro de la cara superior de la celda unitaria tiene las coordenadas x = 1/2, y = 1/2, z = 1. Todos tienen que invertirse para convertir a la combinación más baja de enteros (números enteros); es decir, [221] en la Figura\(\PageIndex{1}\) .17. Finalmente, todos los vectores paralelos tienen la misma dirección del cristal, por ejemplo, los cuatro bordes verticales de la celda que se muestran en la Figura\(\PageIndex{1}\) .17 tienen todos la dirección del cristal [hkl] = [001].
Las direcciones de cristal pueden agruparse en familias. Para evitar confusiones existe una convención en la elección de corchetes que rodean los tres números para diferenciar una dirección de cristal de una familia de direcciones. Para una dirección, se utilizan corchetes [hkl] para indicar una dirección individual. Los corchetes angulares < hkl > indican una familia de direcciones. Una familia de direcciones incluye cualquier dirección que sea equivalente en longitud y tipos de átomos encontrados. Por ejemplo, en una celosía cúbica, las direcciones [100], [010] y [001] pertenecen todas a la <100>familia de planos porque son equivalentes. Si la celosía cúbica se girara 90 ◦, las direcciones a, b y c permanecerían indistinguibles, y no habría manera de decir en qué posiciones cristalográficas están situados los átomos, por lo que la familia de direcciones es la misma. En un cristal hexagonal, sin embargo, este no es el caso, por lo que la [100] y [010] serían ambas <100>direcciones, pero la dirección [001] sería distinta. Finalmente, las direcciones negativas se identifican con una barra sobre el número negativo en lugar de un signo menos.
Planos de cristal
Los planos en un cristal se pueden especificar usando una notación llamada índices Miller. El índice Miller está indicado por la notación [hkl] donde h, k y l son recíprocos del plano con los ejes x, y y z. Para obtener los índices Miller de un plano determinado se requieren los siguientes pasos:
- El plano en cuestión se coloca en una celda unitaria.
- Luego se encuentran sus intercepciones con cada uno de los ejes de cristal.
- Se toma el recíproco de las intercepciones.
- Éstas se multiplican por un escalar para asegurar que está en la relación simple de números enteros.
Por ejemplo, la cara de una celosía que no interseca el eje y o z sería (100), mientras que un plano a lo largo de la diagonal del cuerpo sería el plano (111). Una ilustración de esto junto con los planos (111) y (110) se da en la Figura\(\PageIndex{1}\) .18.
Al igual que con las direcciones cristalinas, las direcciones de los índices Miller pueden agruparse en familias. Los índices individuales de Miller se dan entre paréntesis (hkl), mientras que las llaves {hkl} se colocan alrededor de los índices de una familia de planos. Por ejemplo, (001), (100) y (010) están todos en la familia {100} de planos, para una celosía cúbica.
Descripción de las estructuras cristalinas
Las estructuras cristalinas pueden describirse de varias maneras. La manera más común es referirse al tamaño y la forma de la celda unitaria y las posiciones de los átomos (o iones) dentro de la célula. Sin embargo, esta información a veces es insuficiente para permitir una comprensión de la verdadera estructura en tres dimensiones. La consideración de varias celdas unitarias, la disposición de los átomos entre sí, el número de otros átomos con los que están en contacto y las distancias a los átomos vecinos, a menudo proporcionarán una mejor comprensión. Hay varios métodos disponibles para describir estructuras extendidas en estado sólido. El más aplicable con respecto a semiconductores elementales y compuestos, metales y la mayoría de aislantes es el enfoque de empaquetamiento cercano.
Estructuras empaquetadas: empaque hexagonal y empaque de cierre cúbico
Muchas estructuras cristalinas se pueden describir usando el concepto de empaquetamiento cerrado. Este concepto requiere que los átomos (iones) estén dispuestos de manera que tengan la densidad máxima. Para entender el empaque cercano en tres dimensiones, se debe considerar la manera más eficiente de empaquetar esferas de igual tamaño en dos dimensiones.
La forma más eficiente para que esferas de igual tamaño se empaqueten en dos dimensiones se muestra en la Figura\(\PageIndex{1}\) .19, en la que se puede observar que cada esfera (la esfera sombreada gris oscuro) está rodeada por, y está en contacto con, otras seis esferas (las esferas gris claro en la Figura\(\PageIndex{1}\) .19). Cabe señalar que el contacto con otras seis esferas lo máximo posible es que las esferas sean del mismo tamaño, aunque es posible un empaque de menor densidad. Las capas empaquetadas cercanas se forman por repetición a una hoja infinita. Dentro de estas capas empaquetadas están presentes tres filas empaquetadas, mostradas por las líneas discontinuas en la Figura\(\PageIndex{1}\) .19.
La manera más eficiente para que las esferas de igual tamaño se empaqueten en tres dimensiones es apilar capas empaquetadas una encima de la otra para dar una estructura compacta cerrada. Hay dos formas sencillas en las que esto se puede hacer, dando como resultado estructuras hexagonales o cúbicas empaquetadas.
Cierre hexagonal embalado
Si dos capas empaquetadas cercanas A y B se ponen en contacto entre sí para maximizar la densidad, entonces las esferas de la capa B descansarán en el hueco (vacante) entre tres de las esferas de la capa A. Esto se demuestra en la Figura\(\PageIndex{1}\) .20. Los átomos en la segunda capa, B (gris claro sombreado), pueden ocupar una de dos posiciones posibles (Figura\(\PageIndex{1}\) .20a o b) pero no ambas juntas o una mezcla de cada una. Si se coloca una tercera capa encima de la capa B de tal manera que cubra exactamente la capa A, la posterior colocación de capas dará como resultado la siguiente secuencia... ABABAB... Esto se conoce como empaque hexagonal cerrado o hcp.
La celda hexagonal compacta es un derivado del sistema reticular hexagonal Bravais (Figura\(\PageIndex{1}\) .16) con la adición de un átomo dentro de la celda unitaria en las coordenadas (1/3, 2/3, 1/2). El plano basal de la celda unitaria coincide con las capas empaquetadas cercanas (Figura\(\PageIndex{1}\) .21). En otras palabras, la capa muy empaquetada constituye la familia {001} de planos de cristal.
La fracción de empaquetamiento en una celda empaquetada hexagonal es 74.05%; es decir 74.05% del volumen total está ocupado. La fracción de empaquetamiento o densidad se deriva asumiendo que cada átomo es una esfera dura en contacto con sus vecinos más cercanos. La determinación de la fracción de empaquetamiento se realiza calculando el número de esferas enteras por celda unitaria (2 en hcp), el volumen ocupado por estas esferas y una comparación con el volumen total de una celda unitaria. El número da una idea de cuán abierta o llena es una estructura. En comparación, la fracción de empaquetamiento para cúbico centrado en el cuerpo (Figura\(\PageIndex{1}\) .16) es de 68% y para diamante cúbico (una importante estructura semiconductora que se describirá más adelante) es 34%.
Cupic cerrado: cúbico centrado en la cara
De manera similar a la generación de la estructura hexagonal de empaquetamiento cerrado, se apilan dos capas de empaquetamiento cerrado (Figura\(\PageIndex{1}\) .19) sin embargo, la tercera capa (C) se coloca de tal manera que no cubre exactamente la capa A, mientras se asienta en un conjunto de abrevaderos en la capa B (Figura\(\PageIndex{1}\) .22), luego al repetir la secuencia de empaque será... ABCABCABC... Esto se conoce como empaque de cierre cúbico o ccp.
La celda unitaria de estructura cúbica compacta es en realidad la de una celosía Bravais cúbica centrada en la cara (fcc). En la celosía fcc las capas compactas cercanas constituyen los planos {111}. Al igual que con la fracción de empaquetamiento de celosía hcp en una celda cúbica empaquetada (fcc) es 74.05%. Dado que el cúbico centrado en la cara o fcc se usa más comúnmente en preferencia al cúbico empaquetado cerrado (ccp) en la descripción de las estructuras, el primero se utilizará a lo largo de este texto.
Número de coordinación
El número de coordinación de un átomo o ion dentro de una estructura extendida se define como el número de átomos vecinos más cercanos (iones de carga opuesta) que están en contacto con él. A menudo se usa una definición ligeramente diferente para los átomos dentro de las moléculas individuales: el número de átomos donantes asociados con el átomo o ion central. Sin embargo, esta distinción es bastante artificial, y ambas pueden emplearse.
Los números de coordinación para los átomos metálicos en una molécula o complejo son comúnmente 4, 5 y 6, pero todos los valores de 2 a 9 son conocidos y se han reportado algunos ejemplos de números de coordinación más altos. En contraste, los números comunes de coordinación en estado sólido son 3, 4, 6, 8 y 12. Por ejemplo, el átomo en el centro de la celosía cúbica centrada en el cuerpo tiene un número de coordinación de 8, porque toca los ocho átomos en las esquinas de la celda unitaria, mientras que un átomo en una estructura cúbica simple tendría un número de coordinación de 6. Tanto en las redes fcc como hcp cada uno de los átomos tiene un número de coordinación de 12.
Vacantes octaédricas y tetraédricas
Como se mencionó anteriormente, la fracción de empaque tanto en celdas fcc como hcp es de 74.05%, dejando 25.95% del volumen sin llenar. Los sitios de celosía sin llenar (intersticios) entre los átomos en una célula se denominan sitios intersticiales o vacantes. La forma y tamaño relativo de estos sitios es importante para controlar la posición de los átomos adicionales. Tanto en las células fcc como hcp, la mayor parte del espacio dentro de estos átomos se encuentra dentro de dos sitios diferentes conocidos como sitios octaédricos y sitios tetraédricos. La diferencia entre ambos radica en su número de coordinación, o el número de átomos que rodean cada sitio. Los sitios tetraédricos (vacantes) están rodeados por cuatro átomos dispuestos en las esquinas de un tetraedro. De igual manera, los sitios octaédricos están rodeados por seis átomos que conforman los ápices de un octaedro. Para una celosía cerrada dada, una vacante octaédrica será mayor que una vacante tetraédrica.
Dentro de una celosía cúbica centrada en la cara, los ocho sitios tetraédricos se colocan dentro de la celda, en la coordenada fraccionaria general de (n/4, n/4, n/4) donde n = 1 o 3, por ejemplo, (1/4, 1/ 4, 1/4), (1/4, 1/4, 3/4), etc. Los sitios octaédricos se encuentran en el centro de la celda unitaria (1/2, 1/2, 1/ 2), así como en cada uno de los bordes de la celda, e.g., (1/2 ,0,0). En el sistema hexagonal de empaquetamiento cerrado, los sitios tetraédricos están en (0,0, 3/8) y (1/3, 2/3, 7/8), y los sitios octaédricos están en (1/3, 1/3) , 1/4) y todas las posiciones equivalentes de simetría.
Tipos de estructuras importantes
La mayoría de los materiales cristalinos no tienen una estructura que ts en la red simple de Bravais de un átomo por sitio. Se encuentran otras estructuras cristalinas importantes, sin embargo, solo algunas de estas estructuras cristalinas son aquellas de las cuales ocurren para los semiconductores elementales y compuestos y la mayoría de estas se derivan de redes fcc o hcp. Cada tipo estructural se define generalmente por un arquetipo, un material (a menudo un mineral natural) que tiene la estructura en cuestión y con el que están relacionados todos los materiales similares. Con respecto a los semiconductores elementales y compuestos de uso común, las estructuras importantes son diamante, blenda de zinc, wurtzita y, en menor medida, calcopirita. Sin embargo, la sal de roca, el β -estaño, el cinabrio y el cloruro de cesio se observan como fases de alta presión o alta temperatura y por lo tanto también se discuten. A continuación se ofrece un resumen de estas estructuras. Los detalles de la gama completa de estructuras de estado sólido se dan en otra parte.
Diamante Cúbico
La estructura cúbica de diamante consiste en dos celosías cúbicas interpenetrantes centradas en la cara, con un desplazamiento 1/4 de un cubo a lo largo de la diagonal del cubo También puede describirse como celosía cúbica centrada en la cara en la que la mitad de los sitios tetraédricos se llenan mientras que todos los sitios octaédricos permanecen vacíos. La celda unitaria cúbica de diamante se muestra en la Figura\(\PageIndex{1}\) .23. Cada uno de los átomos (por ejemplo, C) tiene cuatro coordenadas, y la distancia interatómica más corta (C-C) puede determinarse a partir del parámetro de celda unitaria (a).
\[ C-C = a\dfrac{\sqrt{3}}{4} \approx 0.442a \]
Blenda de zinc
Esta es una fase binaria (ME) y lleva el nombre de su arquetipo, una forma mineral común de sulfuro de zinc (ZnS). Al igual que con la red de diamante, la blenda de zinc consiste en las dos celosías fcc interpenetrantes. Sin embargo, en la blenda de zinc una red consiste en uno de los tipos de átomos (Zn en ZnS), y la otra red es del segundo tipo de átomo (S en ZnS). También se puede describir como una red cúbica centrada en la cara de átomos de S en la que la mitad de los sitios tetraédricos están llenos de átomos de Zn. Todos los átomos en una estructura de blenda de zinc son de 4 coordenadas. La celda unitaria de blenda de zinc se muestra en la Figura\(\PageIndex{1}\) .24. Se puede calcular un número de distancias interatómicas para cualquier material con una celda unitaria de blenda de zinc usando el parámetro de celosía (a).
\[ Zn-S = a\dfrac{\sqrt{3}}{4} \approx 0.442a \]
\[ Zn-Zn = \dfrac{a}{\sqrt{2}} \approx 0.707a \]
Calcopirita
El mineral calcopirita CuFes 2 es el arquetipo de esta estructura. La estructura es tetragonal (a = b ≠ c, α = β = γ = 90 ◦, y es esencialmente una superred sobre la de la blenda de zinc. Así, es más fácil imaginar que la red de calcopirita se compone de una red de átomos de azufre en la que los sitios tetraédricos se rellenan en capas,... FeCuFe..., etc. (Figura\(\PageIndex{1}\) .25). En tal estructura idealizada c = 2 a, sin embargo, esto no es cierto para todos los materiales con estructuras de calcopirita.
Sal de roca
Como su nombre lo indica, la estructura arquetípica de sal de roca es NaCl (sal de mesa). En común con la estructura de la blenda de zinc, la sal de roca consiste en dos redes cúbicas interpenetrantes centradas en la cara. Sin embargo, la segunda celosía está desplazada 1/2 a a lo largo del eje de la celda unitaria. También puede describirse como celosía cúbica centrada en la cara en la que se llenan todos los sitios octaédricos, mientras que todos los sitios tetraédricos permanecen vacantes, y así cada uno de los átomos en la estructura de sal de roca tiene 6 coordenadas. La celda unitaria de sal de roca se muestra en la Figura\(\PageIndex{1}\) .26. Se puede calcular un número de distancias interatómicas para cualquier material con una estructura de sal de roca usando el parámetro de celosía (a).
\[ Na-Cl = \dfrac{a}{2} \approx 0.5a \]
\[ Na-Na = Cl-Cl = \dfrac{a}{\sqrt{2}} \approx 0.707a\]
Cinabrio
El cinabrio, llamado así por el arquetipo de sufilde de mercurio, HgS, es una estructura de sal de roca distorsionada en la que la célula resultante es romboédrica (trigonal) teniendo cada átomo un número de coordinación de seis.
Wurtzita
Esta es una forma hexagonal del sulfuro de zinc. Es idéntico en el número y tipos de átomos, pero está construido a partir de dos redes interpenetrantes hcp a diferencia de las redes fcc en la blenda de zinc. Al igual que con la blenda de zinc, todos los átomos en una estructura de wurtzita son de 4 coordenadas. La celda unitaria de wurtzita se muestra en la Figura\(\PageIndex{1}\) .27. Se puede calcular un número de distancias inter atómicas para cualquier material con una celda de wurtzita usando el parámetro de celosía (a).
\[ Zn-S = a\sqrt{\dfrac{3}{8}} \approx 0.612a = \dfrac{3c}{8} = 0.375c\]
\[Zn-Zn = S-S = a = 1.632c\]
No obstante, cabe señalar que estas fórmulas no necesariamente se aplican cuando la relación a/c es diferente del valor ideal de 1.632.
Cloruro de Cesio
La estructura del cloruro de cesio se encuentra en materiales con cationes grandes y aniones relativamente pequeños. Tiene una celda cúbica simple (primitiva) (Figura\(\PageIndex{1}\) .16) con un ion cloruro en las esquinas del cubo y el ion cesio en el centro del cuerpo. Los números de coordinación tanto de Cs+ como de Cl-, con las distancias atómicas internas determinadas a partir de la constante de celosía celular (a).
\[Cs-Cl = \dfrac{a\sqrt{3}}{2} = 0.866a\]
\[Cs-Cs = Cl-Cl = a\]
β-TiN
El alótropo de estaño a temperatura ambiente es β -estaño o estaño blanco. Tiene una estructura tetragonal, en la que cada átomo de estaño tiene cuatro vecinos más cercanos (Sn-Sn = 3.016 Å) dispuestos en un tetraedro muy aplanado, y dos vecinos siguientes más cercanos (Sn-Sn = 3.175 Å). La estructura general del β -estaño consiste en hexágonos fusionados, cada uno unido a su vecino a través de un anillo Sn 4 de cuatro miembros.
Defectos en sólidos cristalinos
Hasta este punto solo nos hemos preocupado por estructuras ideales para sólidos cristalinos en las que cada átomo ocupa un punto designado en la red cristalina. Desafortunadamente, los defectos normalmente existen en equilibrio entre la red cristalina y su entorno. Estos defectos son de dos tipos generales: defectos puntuales y defectos extendidos. Como sus nombres lo indican, los defectos puntuales están asociados con un sitio de celosía de cristal único, mientras que los defectos extendidos ocurren en un rango mayor.
Defectos puntuales: demasiados o muy pocos o simplemente erróneos
Los defectos puntuales tienen un efecto significativo en las propiedades de un semiconductor, por lo que es importante comprender las clases de defectos puntuales y las características de cada tipo. La Figura\(\PageIndex{1}\) .28 resume diversas clases de defectos puntuales nativos, sin embargo, pueden dividirse en dos clases generales; defectos con el número incorrecto de átomos (deficiencia o excedente) y defectos donde la identidad de los átomos es incorrecta.
Impureza intersticial
Una impureza intersticial ocurre cuando se coloca un átomo extra en un sitio reticular que debe estar vacante en una estructura ideal (Figura\(\PageIndex{1}\) .28b). Dado que todos los sitios de celosía adyacentes están llenos, el átomo adicional tendrá que comprimirse en el sitio intersticial, resultando en distorsión de la red y alteración en el comportamiento electrónico local de la estructura. Los átomos pequeños, como el carbono, preferirán ocupar estos sitios intersticiales. Las impurezas intersticiales se difunden fácilmente a través de la red a través de la difusión intersticial, lo que puede resultar en un cambio de las propiedades de un material en función del tiempo. Las impurezas de oxígeno en el silicio generalmente se localizan como intersticiales.
Vacantes
Lo contrario de una impureza intersticial es cuando no hay suficientes átomos en un área particular de la red. Estas se denominan vacantes. Existen vacantes en cualquier material por encima del cero absoluto y aumentan la concentración con la temperatura. En el caso de los semiconductores compuestos, las vacantes pueden ser ya sea vacantes catiónicas (Figura\(\PageIndex{1}\) .28c) o vacantes aniónicas (Figura\(\PageIndex{1}\) .28d), dependiendo del tipo de átomo que falte.
Sustitución
La sustitución de varios átomos en la estructura reticular normal es común, y se usa para cambiar las propiedades electrónicas de los semiconductores compuestos y elementales. Cualquier elemento de impureza que se incorpore durante el crecimiento del cristal puede ocupar un sitio de celosía. Dependiendo de la impureza, los defectos de sustitución pueden distorsionar en gran medida la celosía y/o alterar la estructura electrónica. En general, los cationes intentarán ocupar sitios de retícula catiónica (Figura\(\PageIndex{1}\) .28e), y el anión ocupará el sitio anión (Figura\(\PageIndex{1}\) .28f). Por ejemplo, una impureza de zinc en GaAs ocupará un sitio de galio, si es posible, mientras que un átomo de azufre, selenio y telurio intentaría sustituir a un arsénico. Algunas impurezas ocuparán cualquier sitio indiscriminadamente, por ejemplo, Si y Sn ocupan ambos sitios Ga y As en GaAs.
Defectos antisitio
Los defectos antisitio son una forma particular de defecto de sustitución, y son exclusivos de los semiconductores compuestos. Un defecto antisitio ocurre cuando un catión está fuera de lugar en un sitio de red aniónica o viceversa (Figura\(\PageIndex{1}\) .28g y h). Dependiendo de la disposición, estos se designan como defectos antisitio AB o defectos antisitio BA. Por ejemplo, si un átomo de arsénico está en un sitio de celosía de galio, el defecto sería un defecto de AsGA. Los defectos antisitio implican la unión en un sitio de celosía de átomos de un tamaño diferente al resto de la red, y por lo tanto esto a menudo resulta en una distorsión localizada de la red. Además, los cationes y aniones tendrán un número diferente de electrones en sus conchas de valencia, por lo que esta sustitución alterará la concentración local de electrones y las propiedades electrónicas de esta área del semiconductor.
Defectos extendidos: Dislocaciones en una celosía cristalina
Los defectos extendidos pueden crearse ya sea durante el crecimiento del cristal o como consecuencia de la tensión en la red cristalina. La deformación plástica de los sólidos cristalinos no ocurre de tal manera que todos los enlaces a lo largo de un plano se rompen y reforman simultáneamente. En cambio, la deformación se produce a través de una dislocación en la red cristalina. La Figura\(\PageIndex{1}\) .29 muestra una representación esquemática de una dislocación en una red cristalina. Dos características de este tipo de dislocación son la presencia de un plano de cristal extra, y un gran vacío en el núcleo de la dislocación. Las impurezas tienden a segregarse al núcleo de la dislocación para aliviar la tensión de su presencia.
Epitaxia
Epitaxia, es una transliteración de dos palabras griegas epi, que significa “sobre”, y taxis, que significa “ordenado”. Con respecto al crecimiento cristalino se aplica al proceso de crecimiento de capas cristalinas delgadas sobre un sustrato cristalino. En el crecimiento epitaxial, existe una orientación cristalina precisa del lm en relación con el sustrato. El crecimiento de películas epitaxiales se puede realizar mediante una serie de métodos que incluyen epitaxia de haz molecular, epitaxia de capa atómica y deposición química de vapor, todos los cuales se describirán más adelante.
La epitaxia del mismo material, como un arseniuro de galio lm sobre un sustrato de arseniuro de galio, se denomina homoepitaxia, mientras que la epitaxia donde el lm y el material del sustrato son diferentes se denomina heteroepitaxia. Claramente, en la homoepitaxia, el sustrato y lm tendrán la misma estructura, sin embargo, en la heteroepitaxia, es importante emplear donde sea posible un sustrato con la misma estructura y parámetros reticulares similares. Por ejemplo, el seleniuro de zinc (blenda de zinc, a = 5.668 Å) se cultiva fácilmente sobre arseniuro de galio (blenda de zinc, a = 5.653 Å). Alternativamente, el crecimiento de cristales epitaxiales puede ocurrir donde existe una relación simple entre las estructuras del sustrato y la capa cristalina, tal como se observa entre Al2O3 (100) sobre Si (100). Cualquiera que sea la ruta que se elija, se requiere una coincidencia cercana en los parámetros de la red, de lo contrario, las deformaciones inducidas por el desajuste reticular dan como resultado la distorsión de la lm y la formación de dislocaciones. Si el desajuste es signicante, el crecimiento epitaxial no es energéticamente favorable, provocando que se cultive un lm texturizado o un lm policristalino sin textura. Como regla general, la epitaxia se puede lograr si los parámetros de celosía de los dos materiales están dentro de aproximadamente el 5% uno del otro. Para una epitaxia de buena calidad, esta debe ser inferior al 1%. Cuanto mayor sea el desajuste, mayor será la tensión en el lm. A medida que el lm se vuelve cada vez más grueso, intentará aliviar la tensión en el lm, lo que podría incluir la pérdida de epitaxia del crecimiento de las dislocaciones. Es importante señalar que las <100>direcciones de un lm deben ser paralelas a la <100>dirección del sustrato. En algunos casos, como el Fe sobre MgO, la dirección [111] es paralela al sustrato [100]. La relación epitaxial se especifica dando primero el plano en la película que es paralelo al sustrato [100].
Bibliografía
- Mesas Internacionales para Cristalografía de Rayos X. Vol. IV; Kynoch Press: Birmingham, Reino Unido (1974).
- B. F. G. Johnson, en Química Inorgánica Integral, Pergamon Press, Vol. 4, Capítulo 52 (1973).
- A. R. West, La química del estado sólido y sus aplicaciones, Wiley, Nueva York (1984).


