2.8: Isótopos de hidrógeno
- Page ID
- 69528
Efectos físicos
La presencia de enlaces de hidrógeno intermoleculares proporciona fuerzas de atracción adicionales entre las moléculas. Así, se ven afectadas las propiedades que dependen de las fuerzas intramoleculares.
| Isótopo | Hidrógeno-1 | Hidrógeno-2 | Hidrógeno-3 |
|---|---|---|---|
| Nombre especial | Hidrógeno | Deuterio | Tritio |
| Símbolo | H | D | T |
| Número atómico |
1 |
1 | 1 |
| Número de neutrones | 0 | 1 | 2 |
| Número de masa | 1 | 2 | 3 |
| Abundancia natural | 99.9844% | 0.0156% | muy pequeño |
Síntesis de compuestos de deuterio
Electrólisis de agua
La electrólisis de hidrógeno-1 agua (H 2 O) en presencia de un álcali da como resultado la formación de hidrógeno y oxígeno.
\[ 2 H_2O_{(l)} \rightarrow 2H_{2(g)} + O_{2(g)} \]
De manera similar la hidrólisis del agua deuterada (D 2 O) produce deuterio y oxígeno.
\[ 2D_2O_{(l)} \rightarrow 2 D_{2(g)} + O_{2(g)} \]
Sin embargo, la tasa de electrólisis de D 2 O es ligeramente más lenta que la de H 2 O. Así, la hidrólisis parcial del agua con una mezcla de isótopos naturales da como resultado el ligero enriquecimiento del agua con D 2 O. El nivel de enriquecimiento en un paso es menor al 1%. Para obtener altos niveles de D 2 O (e.g., ca. 30%) es necesario reducir el volumen original de agua en 1/100,000 th.
Equilibrio químico
Las reacciones de intercambio de protones se pueden usar para enriquecer compuestos en deuterio. Por ejemplo, la reacción de HSD con agua mostrada en (2.8.3) tiene una ligera preferencia por la formación de H 2 S, es decir, K eq = 1.012. Así, el burbujeo de HSD a través del agua da como resultado el enriquecimiento del agua en HOD. Sin embargo, alrededor del 30% de enriquecimiento es aproximadamente lo mejor que se puede lograr con este método.
\[ H_2O_{(l)} + HSD_{(g)} \leftrightharpoons HOD_{(l)} + H_2S_{(g)} \]
Destilación fraccionada
El punto de ebullición de H 2 O es (por definición) 100 ◦ C, en contraste el punto de ebullición de D 2 O es 101.4 ◦ C. Así, es posible separar H 2 O de D 2 O por destilación fraccionada. Este método proporciona la ruta más adecuada para un alto enriquecimiento isotópico y de esta manera se puede producir D 2 O de 99.8%.
Nota
El término agua pesada se utiliza para D 2 O de enriquecimiento superior al 99.8%.
Usos de los compuestos de deuterio
Posible fusión nuclear
El mayor uso de D 2 O es como moderador e intercambiador de calor para reactores nucleares de fisión, sin embargo, la mayor aplicación potencial será si la fusión nuclear se realiza como un proceso comercial.
La fusión de dos átomos de deuterio para formar un átomo de helio y energía sería una fuente de energía, (2.8.4), sin embargo, la fusión deuterio-tritio es la más prometedora, (2.8.5).
\[ ^2_1H + ^2_1H \rightarrow ^3_2He + ^1_0n +energy \]
\[ ^2_1H + ^3_1H \rightarrow ^4_2He + ^1_0n +energy \]
La parte deuterio del combustible no plantea un gran problema porque aproximadamente 1 parte de cada 5000 del hidrógeno en el agua de mar es deuterio. Esto equivale a una estimación de que hay más de 10 15 toneladas de deuterio en los océanos. La parte de tritio del combustible es más problemática ya que no existe una fuente natural significativa (Cuadro\(\PageIndex{2}\) .9), y el tritio tendría que obtenerse criando el tritio a partir de litio.
\[ ^6_3Li + ^1_0n \rightarrow ^4_2He + ^3_1H\]
Dado que un galón de agua de mar podría producir tanta energía como 300 galones de gasolina, claramente hay una gran cantidad de energía que potencialmente puede realizarse a través de la fusión nuclear. Desafortunadamente, esta ventaja es también una desventaja ya que las temperaturas alcanzadas son similares a la superficie del sol, lo que vaporizaría cualquier recipiente convencional. Por lo tanto, los experimentos de fusión utilizan un campo magnético para contener la reacción. La forma del campo es como una botella, de ahí el término “botella magnética”.
Un proceso de fusión demostrado es la llamada bomba de hidrógeno o bomba termonuclear en la que se utiliza una bomba atómica de fisión para iniciar una reacción de fusión. La bomba atómica está rodeada por una capa de deuterio de litio. Los neutrones de la explosión atómica (fisión) hacen que el litio se convierta en helio, tritio y energía, (2.8.6). La explosión atómica también suministra la temperatura de 50,000,000 ◦ C necesaria para la posterior fusión de deuterio con tritio, (2.8.5). Entonces, de hecho, la bomba de hidrógeno se llama mal y debería llamarse bomba de deuterio.
Nota
Los cálculos originales para modelar la bomba de hidrógeno se realizaron utilizando ENIAC (abreviatura de Integrador Numérico Electrónico Y Computadora) que originalmente fue diseñado para generar tablas de trayectorias de proyectiles rojos de artillería grande. Las mesas de anillos de artillería fueron hechas por mujeres matemáticas que se llamaban calculadoras de ahí el nombre que se usa hoy en día. Construido en 1946, a menudo se supone que ENIAC es la primera computadora electrónica programable, sin embargo, fue anterior a las seis máquinas Colossus que se utilizaron para descifrar con éxito el código Enigma alemán ya en 1944. No obstante, la existencia de las máquinas Coloso se mantuvo en secreto hasta 1975.
Espectroscopía
En el laboratorio químico los compuestos de deuterio se utilizan comúnmente en espectroscopía para:
a) La asignación de resonancias en espectroscopía IR, Raman y RMN.
b) Como disolvente que no contiene protones en espectroscopía 1H NMR.
A continuación se ofrece una descripción de estas aplicaciones.
Mecanismo de reacción y determinación de la velocidad
Dada la mayor masa de deuterio sobre hidrógeno, existe una dierencia asociada en la velocidad de las reacciones (ver más adelante) y, por lo tanto, las investigaciones que utilizan hidrógeno y análogos de deuterio pueden proporcionar información sobre los mecanismos de reacción.
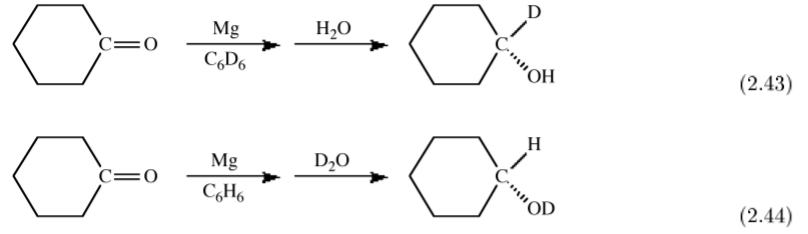
Las dierencias espectroscópicas entre hidrógeno y deuterio también se pueden usar como trazador para determinar de manera única la fuente de sustituyentes particulares. Por ejemplo, la reducción de magnesio (o Grignard) de una cetona produce tras la hidrólisis el alcohol secundario. Si la reacción se lleva a cabo en un disolvente deuterado y H 2 O se usa para la hidrólisis entonces el carbono secundario es deuterado, (2.43). En contraste, si la reacción se lleva a cabo en un disolvente no deuterado y la hidrólisis se logra con D 2 O entonces se forma el alcohol deuterado, (2.44). Estos experimentos definen que la reducción inicial ocurre en el α - carbono de la cetona.
Ejercicio\(\PageIndex{1}\)
Dadas las siguientes reacciones y la distribución isotópica de los productos sugieren el mecanismo de reacción.
\ (\ PageIndex {2}\) .8.1.png” src=” https://chem.libretexts.org/@api/dek...cise_2.8.1.png "/>
- Contestar
-
\ (\ PageIndex {2}\) .8.1 solution.png "src=” https://chem.libretexts.org/@api/dek...1_solution.png "/>
Diferencias entre hidrógeno y deuterio
Propiedades que dependen de las propiedades de los núcleos
El momento magnético nuclear de un núcleo atómico surge de los espines de los protones y neutrones dentro del núcleo. Como consecuencia, los momentos magnéticos para hidrógeno y deuterio son muy diferentes y por lo tanto las condiciones para la detección por RMN son muy diferentes. Así, al observar el espectro de RMN 1H de un compuesto no solo no se observan los átomos de deuterio, sino que ahora el acoplamiento es H-D en lugar de H-H (Figura\(\PageIndex{2}\) .31).
El deuterio es mejor para dispersar neutrones que el hidrógeno. Las secciones transversales H y D son muy distintas y diferentes en signo, lo que permite la variación del contraste en dichos experimentos. La baja densidad de electrones del hidrógeno hace que sea difícil determinar su posición mediante métodos de difracción de rayos X, los métodos de difracción de neutrones permiten una determinación de estructura altamente precisa. El hidrógeno se puede ver por difracción y dispersión de neutrones, sin embargo, tiene una gran sección transversal de neutrones incoherente. Esto es nulo para el deuterio y por lo tanto entrega señales mucho más claras que se pueden obtener para muestras deuteradas. La dispersión de neutrones de muestras deuteradas es indispensable para muchos estudios de macromoléculas en biología.
Propiedades que dependen de la masa
La diferencia de masa entre hidrógeno y deuterio obviamente resulta en una diferencia en la masa molecular de sus compuestos análogos. Esta diferencia puede ser utilizada para el análisis por espectrometría de masas, pero también da como resultado diferentes densidades de compuestos. Por ejemplo, la densidad de H 2 O a 25 ◦ C es de 0.997 g/cm 3, mientras que la densidad de D 2 O a 25 ◦ C es de 1.104 g/cm 3.
La frecuencia vibracional para una molécula diatómica, H-X, se puede definir por la ecuación:
\[ v_{H-X} = \dfrac{1}{2\pi} \sqrt{\dfrac{f_{H-X}}{\mu_{H-X}}}\]
donde f H-X es la constante de fuerza de unión H-X y µ H-X es la masa reducida.
\[ \mu_{H-X} = \dfrac{m_h \cdot m_X}{m_H + m_X} \]
Si se sustituye H por D, la constante de fuerza D-X es la misma que la constante de fuerza H-X, pero la masa reducida es el doble del valor para el enlace H-X. Como resultado, la relación de la frecuencia vibracional de un enlace H-X a la del enlace D-X análogo viene dada por la siguiente ecuación.
\[\dfrac{\mu_{D-X}}{\mu_{H-X}} = (\dfrac{\mu_{H-X}}{\mu_{D-X}})^{\dfrac{1}{2}} = \dfrac{1}{\sqrt{2}} \]
Con el cambio en la energía vibratoria hay un cambio concomitante en la fuerza de unión.
\[ E_{D-X} > E_{H-X} \]
Así, la velocidad de reacciones será más rápida para el derivado de hidrógeno que para el análogo de deuterio. La relación de las constantes de velocidad dependerá de la implicación de la ruptura o formación del enlace H-X en la etapa de limitación de velocidad (la etapa de reacción más lenta dentro del mecanismo de reacción general). Cuando se hace o rompe un enlace H-X en la etapa de limitación de velocidad, entonces la relación de las constantes de velocidad tras la sustitución de deuterio será:
\[ \dfrac{k_{H-X}}{k_{D-X}} \approx 7 \]
Esto se conoce como el efecto isótopo primario. En este caso donde la ruptura o formación del enlace H-X no es parte de la etapa de limitación de velocidad, entonces el efecto isótopo será mucho menor y se conoce como un efecto isótopo secundario.
La posición de las reacciones de equilibrio que implican intercambio de hidrógeno, (2.8.12), se verá afectada por la presencia de deuterio para favorecer que el deuterio se concentre en el enlace más estable. Esta es la base de la concentración de HOD de HSD y agua, (2.8.3).
\[ \text{X-H} + \text{Y-D} \leftrightharpoons \text{X-D} + \text{Y-H} \]
Bibliografía
- M. B. Power, S. G. Bott, J. L. Atwood y A. R. Barron. J. Am. Chem. Soc. , 1990, 112, 3446.
- A. S. Borovik y A. R. Barron, Grupo Principal Chem. 2005, 4, 135.