1.9: Calor y cambios en los estados físicos de la materia
- Page ID
- 77225
Entre los cuatro estados físicos de la materia, el sólido tiene la menor energía térmica. Las fuerzas intermoleculares en los sólidos son fuertes y no dejan que las moléculas se deslicen entre sí. Las moléculas y los enlaces en ellas aún pueden tener movimientos vibratorios que dan cuenta del contenido de energía térmica del material.
La temperatura refleja el contenido de energía térmica del material: la adición de calor aumenta los movimientos vibratorios y la temperatura aumenta. En última instancia, el sólido cambia a líquido y el líquido cambia a una fase gaseosa a medida que se agrega más calor, como se ilustra en la Figura 1.9.1.
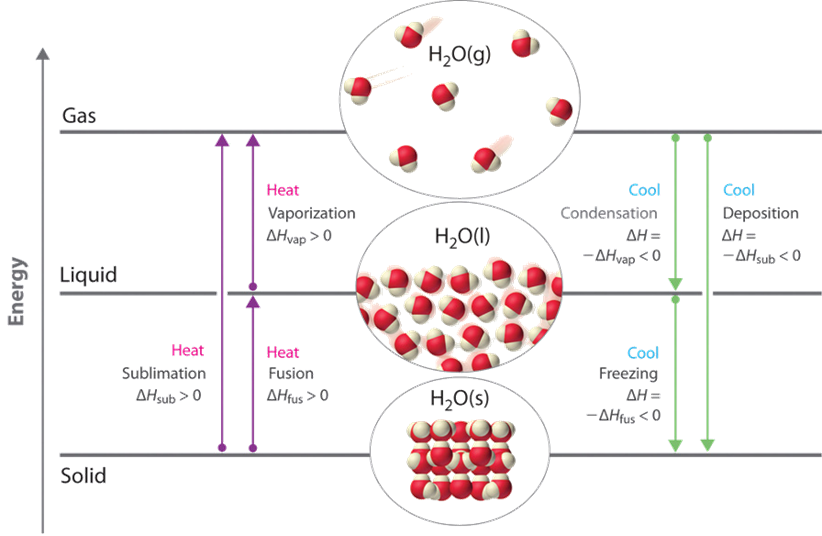
Fusión y congelación
Cuando la temperatura alcanza el punto de fusión del sólido al calentarse, la temperatura no aumenta más, pero el vendido cambia gradualmente a la fase líquida. El calor agregado en el punto de fusión se usa para cambiar las partículas de una forma bien dispuesta en el sólido a una disposición irregular en la fase líquida. Este proceso se llama fusión de sólidos.
La energía necesaria para fundir una cantidad unitaria de la sustancia es el calor de fusión (∆H fus).
El calor de fusión generalmente se expresa en las unidades de julios por gramo (\(\frac{J}{g}\)) para la cantidad unitaria en gramos o en julios por mol (\(\frac{J}{mol}\)) para la cantidad unitaria en moles.
Si se elimina calor de una sustancia en su punto de fusión, ocurre lo contrario de la fusión, es decir, la congelación, es decir, el líquido cambia gradualmente de fase líquida a sólida. La energía igual al calor de fusión se libera durante el proceso de congelación. La Fig. 1.9.2 muestra hielo y agua a 0 o C, un ejemplo de fusión y congelación.

Vaporización y condensación
Después de la fusión, la adición de calor provoca un aumento en la temperatura del líquido hasta que se alcanza el punto de ebullición. Algunas de las moléculas en un líquido tienen energía cinética lo suficientemente alta como para cruzar el límite líquido-gas y convertirse en fase gaseosa. Este proceso se llama vaporización.
La energía necesaria para evaporar una cantidad unitaria de un líquido se llama calor de vaporización (∆H vap).
El calor de vaporización suele expresarse en las unidades de julios por gramo (\(\frac{J}{g}\)) para la cantidad unitaria en gramos o julios por mol (\(\frac{J}{mol}\)) para la cantidad unitaria en moles.
El reverso de la evaporación se llama condensación, que libera calor igual al calor de vaporización. La Fig. 1.9.3 demuestra la coexistencia de bromo en fase líquida y gaseosa a temperatura ambiente a través de los procesos simultáneos de evaporación y condensación.
Cuando la temperatura alcanza el punto de ebullición del líquido, la temperatura no aumenta más, sino que el calor agregado se usa para evaporar el líquido. El calentamiento aumenta la temperatura de la fase gaseosa después de que todo el líquido haya cambiado a la fase gaseosa.

Sublimación y deposición
El sólido puede cambiar directamente a la fase gaseosa sin pasar por la fase líquida. Este proceso se llama sublimación.
La energía requerida en la sublimación (∆H sub) es la adición del calor de fusión y el calor de vaporización, es decir:
\[\Delta H_{\text {sub }}=\Delta H_{\text {fus}}+\Delta H_{\text {vap }}\nonumber\]
El reverso de la sublimación se llama deposición, es decir, la fase gaseosa cambia directamente a la fase sólida. La Fig. 1.8.4 muestra la sublimación de cristales de yodo sobre una placa caliente y la deposición de gas yodo sobre un vidrio de reloj helado.

La sublimación se encarga de secar la ropa por debajo de 0 o C condiciones en zonas frías. La sublimación también se utiliza en la liofilización de verduras y otros alimentos. Las bacterias no pueden crecer en los alimentos secos porque necesitan algo de humedad para crecer. La Fig. 1.9.5 muestra las terminologías relacionadas con los cambios de fase descritos en los párrafos anteriores.

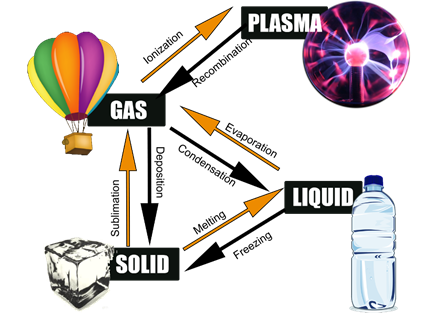
Curva de calentamiento
Una presentación gráfica de la relación del calor agregado frente al cambio de temperatura y los cambios de fase de una materia se denomina curva de calentamiento.
La Fig. 1.9.6 muestra la curva de calentamiento del agua. La curva muestra el calentamiento del hielo inicialmente, seguido de la coexistencia de sólido y líquido en el punto de liberación, luego odiando el agua líquida, luego coexistiendo las fases líquida y gaseosa en el punto de ebullición, y finalmente el calentamiento del vapor —la fase gaseosa del agua. El reverso de la curva de calentamiento se llama curva de enfriamiento.
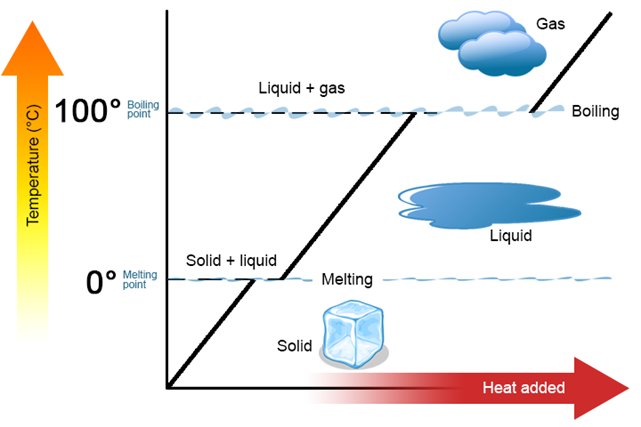
Cálculos de calor en curvas de calentamiento o enfriamiento
El calor requerido o liberado se puede calcular usando el calor específico de las fases sólida, líquida y gaseosa de la sustancia. El calor de fusión es necesario en el punto de congelación, y el calor de evaporación es necesario en el punto de ebullición de la sustancia. El cálculo del calor se explica en el siguiente ejemplo.
Calcular la energía requerida para calentar 10.0 g de hielo de -20.0 o C a vapor (vapor de agua) a 110 o C?
Solución
1er paso: calentar el hielo desde -20.0 o C hasta el punto de fusión del hielo, es decir, 0.00 o C:
m = 10.0 g, C s de hielo = 2.06\(\frac{J}{g \cdot{ }^{\circ} \mathrm{C}}\), ∆T = 0.00 o C — (-20.0 o C) = 20.0 o C
\[\mathrm{q}_{1}=\mathrm{C}_{\mathrm{s}} \mathrm{m} \Delta \mathrm{T}=2.06 \frac{J}{g \cdot{ }^{\circ} \mathrm{C}}\times 10.0 \mathrm{~g} \times 20.0^{\circ} \mathrm{C}=412 \mathrm{~J}\nonumber\]
2º paso — derretimiento del hielo, multiplica el calor de fusión con la cantidad de sustancia:
m = 10.0 g, ∆H fus = 334\(\frac{J}{g}\).
\[\mathrm{q}_{2}=\Delta \mathrm{H}_{\text {fus }} \times \mathrm{m}=334\frac{J}{g}\ \times 10.0 \mathrm{~g}=3340 \mathrm{~J}\nonumber\]
3er paso —odiar el agua desde 0.00 o C hasta el punto de ebullición del agua, es decir, 100 o C:
m = 10.0 g, C s de agua líquida = 4.184\(\frac{J}{g \cdot{ }^{\circ} \mathrm{C}}\), ∆T = 100 o C — 0.00 o C = 100 o C
\[\mathrm{q}_{3}=\mathrm{C}_{\mathrm{s}} \mathrm{m} \Delta \mathrm{T}=4.184 \frac{J}{g \cdot{ }^{\circ} \mathrm{C}}\times 10.0 \mathrm{~g} \times 100^{\circ} \mathrm{C}=4180 \mathrm{~J}\nonumber\]
4º paso — ebullición de agua líquida, multiplicar el calor de vaporización con la cantidad de la sustancia:
m = 10.0 g, ∆H vap = 2260\(\frac{J}{g}\)
\[\mathrm{q}_{4}=\Delta \mathrm{H}_{\text {vap }} \times \mathrm{m}=2260 \frac{J}{g}\ \times 10.0 \mathrm{~g}=22600 \mathrm{~J}\nonumber\]
5º paso —odiar el tallo de 100 o C a 110 o C:
m = 10.0 g, C s de vapor = 2.00\(\frac{J}{g \cdot{ }^{\circ} \mathrm{C}}\), ∆T = 110 o C — 100 o C = 10.0 o C
\[\mathrm{q}_{5}=\mathrm{C}_{\mathrm{s}} \mathrm{m} \Delta \mathrm{T}=2.00\frac{J}{g \cdot{ }^{\circ} \mathrm{C}} \times 10.0 \mathrm{~g} \times 10.0^{\circ} \mathrm{C}=200 \mathrm{~J}\nonumber\]
Calor total necesario =\(q_{1}+q_{2}+q_{3}+q_{4}+q_{5}=412 \mathrm{~J}+3340 \mathrm{~J}+4180 \mathrm{~J}+22600 \mathrm{~J}+200 \mathrm{~J}=30700 \mathrm{~J}\)
\[30700 \mathrm{~J} \times \frac{1 \mathrm{~kJ}}{1000 \mathrm{~J}}=30.7 \mathrm{~kJ}\nonumber\]
La porción más significativa del calor se consume en hervir el agua a vapor, es decir, 22.6 kJ de 30.7 kJ total. La misma cantidad de calor se libera cuando el vapor se condensa. Es por ello que la quemadura de vapor es mucho más severa que la quemadura por agua caliente.


