1.8: El calor y sus medidas
- Page ID
- 77210
El calor es energía en transferencia hacia y desde un sistema termodinámico por un mecanismo distinto al trabajo o la transferencia de materia.
La energía existe en diferentes formas, pero la energía se transforma de una forma a otra a través del trabajo o el calor. En las reacciones químicas, una porción significativa de la transferencia de energía ocurre a través del calor. Las hojas verdes en las plantas atrapan la energía de la luz y la almacenan como energía química en forma de glucosa sintetizada a partir de agua y dióxido de carbono, como se ilustra en la Fig. 1.8.1.
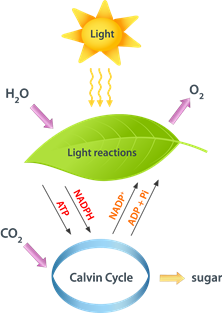
Un proceso inverso ocurre cuando comemos alimentos, es decir, las sustancias alimenticias se convierten en dióxido de carbono, agua y energía, como se ilustra en la Fig. 1.8.2. Se utiliza algo de energía para mantener nuestra temperatura corporal a un nivel promedio. Otra porción es utilizada para impulsar reacciones químicas que consumen energía y sintetizan las sustancias que necesitamos.
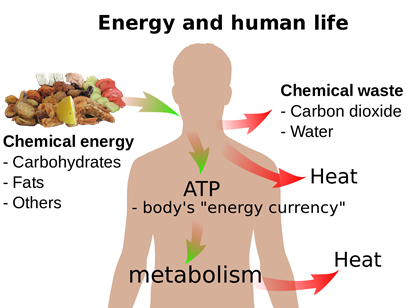
Temperatura Corporal
El cuerpo humano pierde continuamente energía como calor al medio ambiente. El calor liberado por las reacciones exotérmicas en el proceso de digestión de los alimentos suministra el calor necesario para mantener la temperatura corporal en un nivel promedio. La temperatura corporal humana varía en un rango pequeño, como se ilustra en la Fig. 1.8.3. La hipotermia es de 37.5 <35.0 °C (95.0 °F), normal body temperate is 36.5—37.5 °C (97.7—99.5 °F), fever and hyperthermia is > o 38.3 °C (99.5 o 100.9 °F), la hiperpirexia es >40.0 o 41.0 °C (104.0 o 105.8 °F).
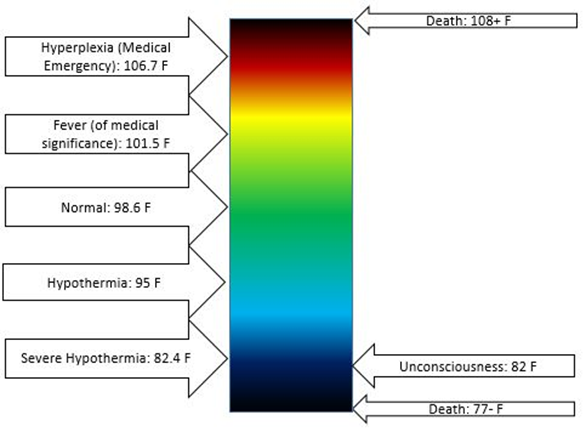
Medición de calor
La temperatura es una manifestación de la energía térmica de un objeto, pero la temperatura y la energía no son las mismas. La temperatura es una medida de picor o frialdad, y es intensiva, y la energía es una propiedad física extensa de la materia. Por ejemplo, 1 g de agua tiene algo de energía, pero 2 g de agua a la misma temperatura tiene el doble de energía.
Calor específico
La caloría (c o cal) es una unidad no SI de calor, trabajo y energía.
La energía necesaria para elevar la temperatura de 1 g de agua en 1 o C es de 1 caloría
El calor necesario para elevar la temperatura de 2 g de agua en 1 o C es de 2 calorías, y para elevar la temperatura de 2 g de agua en 2 o C es de 4 calorías. Es decir, la energía térmica (q) es directamente proporcional tanto a la masa (m) como al cambio de temperatura (∆T) de un objeto:
\ begin {ecuación}
q\ propto m\ Delta T\ nonumber
\ end {ecuación}
Introduciendo una constante de proporcionalidad, es decir, calor específico (C s) cambia la proporcionalidad a igualdad, que se conoce como la ecuación del calor:
\ begin {ecuación}
q=c_ {s} m\ Delta T\ nonumber
\ end {ecuación}
, donde C s es Calor Específico.
La energía térmica necesaria para elevar la temperatura de 1g de una sustancia en 1 o C (o 1K) es calor específico si la sustancia.
La forma matemática de la definición de calor específico es:
\ begin {ecuación}
C_ {S} =\ frac {q} {m\ Delta T}\ nonumber
\ end {ecuación}
Las unidades de calor específico son\(\frac{c a l}{g .^{\circ} \mathrm{C}}\), donde cal es una unidad de energía no SI. La unidad de energía SI es el joule (J). La siguiente es una relación exacta entre calory y joule:
\ begin {ecuación}
1\ mathrm {~cal} =4.184\ mathrm {~J}\ texto {(exacto)}\ nonumber
\ end {ecuación}
Entonces, el calor específico (C s) en unidades SI es:\(\frac{J}{g \cdot^{o} C}\)
La unidad energética en nutrición y alimentación es la caloría alimenticia o Calory (C) que se escribe con C mayúscula, y es igual a 1000 cal, es decir,
\ begin {ecuación}
\ mathrm {C} =1000\ mathrm {~cal} =1\ mathrm {~kcal} =4184\ mathrm {~J}\ nonumber
\ end {ecuación}
, donde la letra C mayúscula es calory de alimentos.
El calor específico es una propiedad física característica de un material. Varía porque las energías de los movimientos vibratorios de los enlaces y otros movimientos que contribuyen al contenido de energía térmica difieren de material a material. En el Cuadro 1 se enumeran calores específicos de algunos materiales familiares.
El agua tiene mayor calor específico que otros materiales, es decir, absorbe o libera más calor para el mismo cambio de temperatura. La variación de temperatura ambiental se mantiene moderada en las zonas costeras debido a que el cambio de temperatura del agua es menor para la misma cantidad de energía absorbida o liberada. Tenga en cuenta que el calor específico del agua líquida es diferente del agua sólida (hielo) y el agua gaseosa (vapor).
|
Sustancia |
Calor específico (\(\frac{J}{g \cdot^{o} C}\)) |
|---|---|
|
Al |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
0.902 |
|
C (grafito) |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
0.720 |
|
Fe |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
0.451 |
|
Cu |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
0.385 |
|
Au |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
0.128 |
|
NH 3 (amoníaco) |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
4.70 |
|
H 2 O (líquido) |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
4.184 |
|
H 2 O (hielo) |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
2.06 |
|
H 2 O (vapor) |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
2.00 |
|
C 2 H 5 OH (l) (etanol) |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
2.46 |
|
(CH 2 OH) 2 (l) (etilenglicol, anticongelante) |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
2.42 |
|
CCl 4 (tetracloruro de carbono) |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
0.861 |
|
Madera |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
1.76 |
|
Concreto |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
0.88 |
|
Vidrio |
\ (\ frac {J} {g\ cdot^ {o} C}\))” valign="top” width="93" class="lt-chem-372555">
0.84 |
Cálculos usando calor específico
Los valores de calor específicos se utilizan en la ecuación de calor (\(q=C_{s} m \Delta T\)) para calcular el cambio de temperatura para una cantidad dada de calor o la energía térmica necesaria para un cambio de temperatura dado de un material. Se usa comúnmente un calorímetro de taza de café ilustrado en la Fig. 1.8.4. Consiste en una taza de café con tapa. Contiene agua en la que se sumerge el objeto caliente o frío, o se realiza una reacción química para el intercambio de calor con el agua. Se utiliza un bucle de alambre para remover el agua. Un termómetro registra el cambio en la temperatura del agua. El calor absorbido o liberado por el agua se calcula a partir de los datos de masa, calor específico y cambio de temperatura del agua.
La inmersión de un objeto caliente en 50.0 gramos de agua en un calorímetro de taza de café aumentó la temperatura del agua de 22.0 o C a 28.8 o C. ¿Cuánto calor gana o pierde el agua?
Solución
Dado: m = 50.0 g agua, C s = 4.184 (\ frac {J} {g\ cdot^ {o} C}\), ∆T = T f — T i = 28.8 o C — 22.0 o C = 6.8 o C, Deseada: calor ganado o perdido por el agua, es decir, q agua =?
Cálculos:
\ begin {ecuación}
\ mathrm {q} _ {\ texto {agua}} =\ mathrm {C} _ {\ mathrm {s}}\ mathrm {m}\ Delta\ mathrm {T} =4.184\ frac {\ mathrm {J}} {\ mathrm {g} {} ^ {\ circ}\ mathrm {C}}\ times 50.0\ mathrm {g}\ veces 6.8^ {\ circ}\ mathrm {C} =+1400\ mathrm {~J}\ nonumber
\ end {ecuación}
El signo +ve dice que el agua ganó 1400 J de calor.
El nitrato de amonio (NH 4 NO 3) se utiliza como paquete frío en los hospitales para disminuir la temperatura de un área específica de la piel. Cuando se disuelven 3.21 g de NH 4 NO 3 en 50.0 g de agua en un calorímetro de taza de café a 25.0 o C, la temperatura disminuye a 20.4 o C. ¿Cuál es la cantidad de calor absorbido o liberado por el agua?
Solución
Dado: m de solución = 50.0g H 2 O + 3.21 g NH 3 NO 3 = 53.2 g, C s = 4.184 (\ frac {J} {g\ cdot^ {o} C}\), ∆T = T f — T i =20.4 o C - 25.0 o C = -4.6 o C, Deseada: calor ganado o perdido por el solución, es decir, q solución =?
Cálculos:
\ begin {ecuación}
\ mathrm {q} _ {\ text {solución}} =\ mathrm {C} _ {\ mathrm {s}}\ mathrm {m}\ Delta\ mathrm {T} =4.184\ frac {\ mathrm {J}} {g^ {\ circ}\ mathrm {C}}\ times 53.2\ mathrm {~g}\ veces\ izquierda (-4.6^ {\ circ}\ mathrm {C}\ derecha) =-1.0\ veces 10^ {3}\ mathrm {~J}\ nonumber
\ end {ecuación}
El signo —ve dice que el agua perdió calor
En los problemas que implican el calentamiento de la solución, la masa de solución incluye la masa de agua y el soluto. Se supone que el calor específico y la densidad de la solución diluida son los mismos que el del agua pura.
El cloruro de calcio (CaCl 2) se utiliza como paquete caliente, es decir, para elevar la temperatura de una porción específica de la piel. Cuando CaCl 2 se disuelve en agua, el calor es liberado por el proceso y absorbido por el agua circundante, aumentando la temperatura del agua.
Cuando 5.00 g de CaCl 2 se disuelven en 50.0 g de agua a 23 o C en un calorímetro de taza de café, la temperatura sube a 39.2 o C. ¿Cuál es la cantidad de calor absorbido o liberado por el agua?
Solución
Dado: m de solución = 50.0g H 2 O + 5.00 g CaCl 2 = 55.0 g, C s = 4.184 (\ frac {J} {g\ cdot^ {o} C}\), ∆T = T f — T i =39.2 o C - 23.0 o C = 16.2 o C, Deseada: calor ganado o perdido por la solución, es decir, q solución =?
Cálculos:
\ begin {ecuación}
\ mathrm {q} _ _ {\ text {solución}} =\ mathrm {C} _ {\ mathrm {s}}\ mathrm {m}\ Delta\ mathrm {T} =4.184\ frac {\ mathrm {J}} {g. ^ {\ circ}\ mathrm {C}}\ veces 55.0\ mathrm {~g}\ veces\ izquierda (16.2^ {\ circ}\ mathrm {C}\ derecha) =3.7\ veces 10^ {3}\ mathrm {~J}\ nonumber
\ end {ecuación}
El signo +ve dice que el agua ganó calor.
La energía liberada de los alimentos
Los alimentos y los combustibles fósiles son compuestos de carbono e hidrógeno y también pueden contener algunos otros elementos como oxígeno, nitrógeno, fósforo y azufre. Los combustibles se utilizan en las reacciones de combustión para liberar calor para diferentes propósitos. Las mismas reacciones de combustión ocurren en los sistemas vivos en varios pasos para obtener energía de los alimentos. Por ejemplo, la ecuación química para la combustión de glucosa es:
\[\ce{C6H12O6 (s) + 6O2 (g) -> 6CO2 (g) + 6H2O (l)}\quad\Delta \mathrm{H}^{\circ}=-2803 \mathrm{~kJ}\nonumber\]
, donde ∆H o es la entalpía de reacción, es decir, el calor desprendido o absorbido en condiciones de presión constante. Esta reacción libera 2803 kJ de energía como calor por mol de glucosa. El signo —ve de ∆H o indica que la reacción libera la energía, es decir, la reacción es exotérmica. La misma cantidad de energía se libera cuando la glucosa es digerida y convertida en los mismos productos en el sistema vivo bajo las mismas condiciones.
Medición de la energía liberada de los alimentos
El calor liberado de la combustión de una sustancia se mide utilizando un calorímetro de bomba ilustrado en la Fig. 1.8.5. La sustancia se coloca en una celda particular rodeada de un exceso de oxígeno. Una chispa eléctrica enciende la sustancia, y el calor liberado provoca un aumento de temperatura en el agua y los demás materiales en el medidor. La capacidad calorífica (C cp), es decir, el producto del calor y masa específicos promedio del medidor y los componentes del agua, se calibra antes del experimento. El calor liberado de la cantidad dada de la sustancia se calcula a partir de la capacidad calorífica y el incremento templado medido.
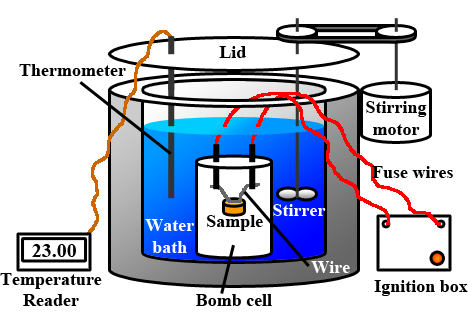
El calor de combustión por g de un alimento se llama el valor de combustible del alimento
La glucosa es uno de los carbohidratos. Los carbohidratos son componentes de los alimentos que son compuestos de carbono, hidrógeno y oxígeno en los que la proporción de hidrógeno a oxígeno es de 2 a 1. El valor promedio de combustible de los carbohidratos es de 17 kJ/g.
La segunda clase principal de alimentos es la grasa. Por ejemplo, la ecuación química de la triesterina C 57 H 110 O 6, que es una grasa, es:
\[\ce{2C57H110O6 (s) + 16O2 (g) -> 114CO2 (g) + 110H2O (l)}\quad\Delta \mathrm{H}^{\circ}=-71609 \mathrm{~kJ}\nonumber\]
El signo —ve con valor energético indica que la energía se libera, o la reacción es exotérmica. El valor promedio de combustible de las grasas es de 38 kJ/g.
El tercer tipo primario de alimento es la proteína. La proteína se utiliza principalmente como material de construcción en los sistemas vivos, pero también se usa como fuente de energía. El valor promedio de combustible de la proteína es de 17 kJ/g.
Los valores promedio de combustible de los tres componentes principales de los alimentos se enumeran en el Cuadro 2. Estos valores se utilizan para calcular el valor fule de las porciones de alimentos, como se explica en los siguientes ejemplos.
|
Alimentos |
Valor de combustible kJ/g |
|---|---|
|
Carbohidratos |
17 |
|
Proteínas |
17 |
|
Grasas |
38 |
Calcula la energía liberada de una taza de jugo de naranja que contiene 26 g de carbohidratos, sin grasa y 2 g de proteína.
Solución
Carbohidrato:\(26 \mathrm{~g} \times 17 \mathrm{~kJ} / \mathrm{g}=442 \mathrm{~kJ}\)
Proteína: Energía\(\quad\ 2 \mathrm{~g} \times 17 \mathrm{~kJ} / \mathrm{g}=34 \mathrm{~kJ}\)
total liberada\(\quad\quad=476 \mathrm{~kJ}\)
El valor energético en kJ se puede convertir en calorías de los alimentos (C) mediante el uso del factor de conversión basado en las siguientes relaciones.
\ begin {ecuación}
\ texto {caloría alimenticia C} =1000\ mathrm {~cal} =1\ mathrm {~kcal} =4184\ mathrm {~J}\ nonumber
\ end {ecuación}