4.7: Cálculos estequiométricos

Última actualización
Guardar como PDF

Page ID: 77183

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Factores de conversión a partir de una ecuación química

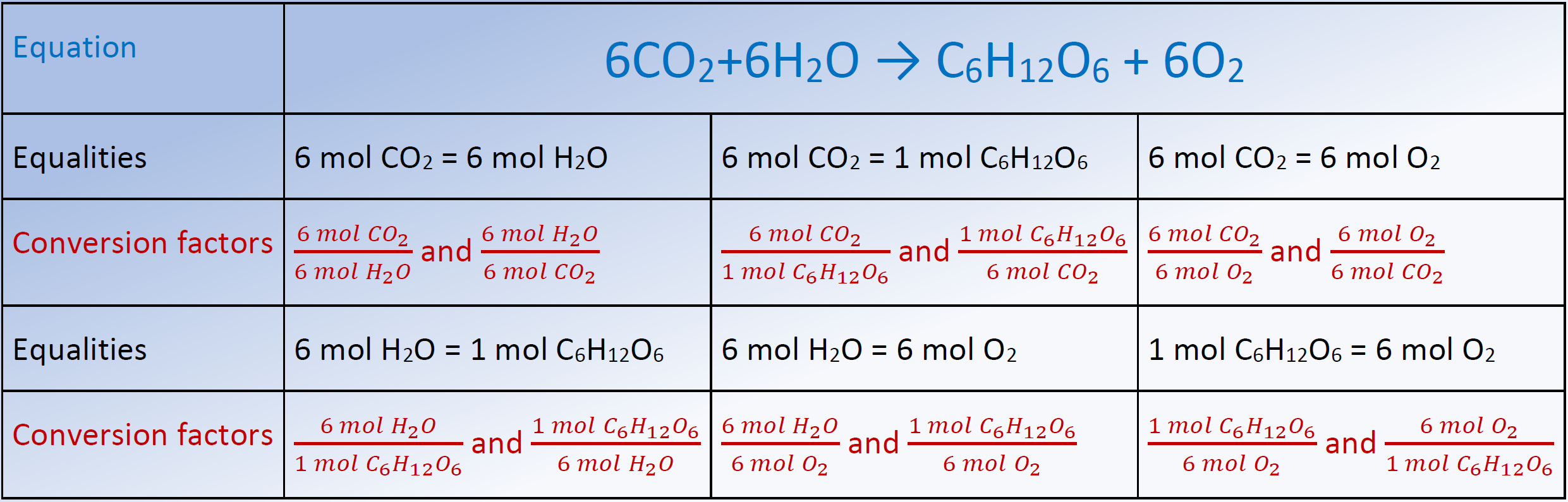
La estequiometría pronunciada como “stɔɪkiˈmɪtri” es el cálculo de la cantidad de reactivos y productos en una reacción química. Se basa en el hecho de que una ecuación química equilibrada es también un conjunto de igualdades mol a mol entre los reactivos y los productos. Cada igualdad da dos factores de conversión que permiten calcular el mol de una sustancia a partir del mol dado de cualquier otra sustancia en la ecuación.

La Fig. 4.6.1 enumera la ecuación química para la reacción de fotosíntesis, las ecualidades de mol a mol de la ecuación y los dos factores de conversión de cada una de las iguales, como ejemplo. Los factores de conversión se utilizan para calcular la cantidad desconocida en el mol a partir de la cantidad conocida en el mol de cualquier otro reactivo o producto en la misma ecuación química, como se explica en los siguientes ejemplos.

Factores estequiométricos a partir de una ecuación de reacción de fotosíntesis equilibrada — Figura\(\PageIndex{1}\): Ecuación química equilibrada de la reacción de fotosíntesis, igualaciones mol a mol y factores de conversión derivados de la ecuación.

Conversión de topo a mol a partir de una ecuación química

El cálculo del mol de la sustancia deseada a partir del mol dado de cualquier reactivo o producto necesita un factor de conversión. Los pasos son:

escribir la cantidad dada y la cantidad deseada,
escribir la ecuación química equilibrada,
escribir la igualdad entre lo dado y las sustancias deseadas,
derecho el factor de conversión que tiene la sustancia dada en el denominador y la sustancia deseada en el numerador,
multiplicar la cantidad dada con el factor de conversión. Verifique dos veces para asegurarse de que cancela la sustancia dada y deje la sustancia deseada en la respuesta.

Ejemplo\(\PageIndex{1}\)

¿Calcular los moles de glucosa producidos a partir de 3.0 moles de dióxido de carbono en la reacción de fotosíntesis?

Solución

i. Dado: 3.0 mol CO ₂, Deseado:? moles de C ₆ H ₁₂ O ₆

ii. Ecuación química:\(\ce{6CO2 + 6H2O -> C6H12O6 + 6O2}\)

iii. La igualdad deseada: 6 mol CO ₂ = 1 mol C ₆ H ₁₂ O ₆,

iv. Factor de conversión deseado:\(\frac{1 \mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}{6 \mathrm{~mol} \mathrm{~CO_2}}\)

v. Cálculos:\[3.0 \cancel{\mathrm {~mol~CO_2}} \times \frac{1 \mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}{6 \cancel{\mathrm{~mol} \mathrm{~CO_2}}}=0.50 \mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}\nonumber\]

Ejemplo\(\PageIndex{2}\)

El magnesio reacciona con HCl por esta reacción:\(\ce{Mg(s) + 2HCl(aq) -> MgCl2(aq) + H2(g)^}\). Calcular los moles de Mg necesarios para producir 3 moles de H ₂?

Solución

i. Dado: 3 mol de H ₂. Deseado:? Moles de Mg.

ii. Se da la ecuación química.

iii. La igualdad deseada: 1 mol Mg = 1 mol H ₂.

iv. El factor de conversión deseado:\(\frac{1 ~mol~Mg}{1 ~mol{~H}_{2}}\)

v. Cálculo:\[3 \cancel{\mathrm{~mol} \mathrm{~H}_{2}} \times \frac{1 \mathrm{~mol} \mathrm{~Mg}}{1 \cancel{\mathrm{~mol} \mathrm{~H}_{2}}}=3 \operatorname{~mol} ~M g\nonumber\]

Conversión de moles a masa a partir de una ecuación química

Los cálculos descritos en los dos ejemplos anteriores muestran el cálculo de moles de la sustancia deseada a partir de los moles de la sustancia dada usando un factor de conversión a partir de una ecuación química. La masa molar es un factor de conversión de un mol a gramo de la sustancia. Entonces, agregar una masa molar de la sustancia deseada como segundo factor de conversión, como se explica en los siguientes ejemplos. Verifique que todas las unidades cancelen, dejando la unidad de masa de la sustancia deseada en la respuesta final.

Ejemplo\(\PageIndex{3}\)

Calcular gramos de precipitado de AgCl formado a partir de 2,0 moles de CaCl ₂ consumidos en la siguiente reacción:\[\ce{2AgNO3 + CaCl2 -> Ca(NO3)2 + 2AgCl(s)(v)}\nonumber\]

Solución

i. Dado: 2.0 moles de CaCl ₂. Deseado:? g AgCl

ii. Masa molar de AgCl = 1x107.87 g Ag.mol ^-1 + 1x35.45 g C.Mol ^-1 = 143.3 g AgCl.mol ^-1

iii. Se da la ecuación química.

iv. La igualdad deseada: 1 mol CaCl ₂ = 2 mol de AgCl, y 1 mol de AgCl =143.3 g AgCl.

v. Los factores de conversión deseados:\[\frac{2 \mathrm{~mol} \mathrm{~AgCl}}{1 \mathrm{~mol} \mathrm{~CaCl}_{2}} \quad\text { and }\quad \frac{143.3 \mathrm{~g} \mathrm{~AgCl}}{1 \mathrm{~mol} \mathrm{~AgCl}}\nonumber\]

vi. Cálculo:\[2.0\cancel{\mathrm{~mol}\mathrm{~CaCl}_{2}}\times\frac{2 \cancel{\mathrm{~mol} \mathrm{~AgCl}}}{1 \cancel{\mathrm{~mol} \mathrm{~CaCl}_{2}}} \times\frac{143.3 \mathrm{~g} \mathrm{~AgCl}}{1 \cancel{\mathrm{~mol} \mathrm{~AgCl}}}=573.3 \mathrm{~g} \mathrm{~AgCl}\nonumber\]

Ejemplo\(\PageIndex{4}\)

¿Cuántos gramos de dióxido de carbono se necesitan para reaccionar con 2 moles de agua en la reacción de fotosíntesis?

Solución

i. Dado: 2.0 moles de H ₂ O Deseado:? g CO ₂.

ii. Masa molar de CO ₂ = 1x12.011 g C.mol ^-1 + 2x15.999 g O.mol ^-1 = 44.009 g CO ₂ .mol ^-1

iii. La ecuación química:: 6CO ₂ + 6 H ₂ O → C ₆ H ₁₂ O ₆ + 6O ₂.

iv. La igualdad deseada: 6 mol CO ₂ = 6 mol H ₂ O, y 1 mol CO ₂ = = 44.009 g CO ₂.

v. Los factores de conversión deseados:\[\frac{6 \mathrm{~mol} \mathrm{~CO}_{2}}{6 \mathrm{~mol} \mathrm{~H}_{2}}\mathrm{O}\quad \text { and }\quad \frac{44.009 \mathrm{~g} \mathrm{~CO}_{2}}{1 \mathrm{~mol} \mathrm{~CO}_{2}}\nonumber\]

vi. Cálculo:\[2.0 \cancel{\mathrm{~mol} \mathrm{~} \mathrm{H}_{2} \mathrm{O}} \times \frac{6 \cancel{\mathrm{~mol} \mathrm{~CO}_{2}}}{6 \cancel{\mathrm{~mol} \mathrm{~H}_{2} \mathrm{O}}} \times \frac{44.009 \mathrm{~g} \mathrm{~CO}_{2}}{1 \cancel{\mathrm{~mol} \mathrm{~CO}_{2}}}=88 \mathrm{~g} \mathrm{~CO}{ }_{2}\nonumber\]

Conversión de masa a masa a partir de una ecuación química

Una ecuación química da un factor de conversión de mol a mol. Si la sustancia dada está en gramos y la sustancia deseada también está en gramos, entonces se necesitan dos factores de conversión adicionales basados en las masas molares. Es decir, se necesitan las siguientes conversiones:

Masa de sustancia dada"mol de la sustancia dada"mol de la sustancia deseada"gramos de la sustancia deseada.

La masa molar recíproca de la sustancia dada es el primer factor de conversión, el factor de conversión mol a mol de la ecuación química es el segundo factor de conversión, y la masa molar de la sustancia deseada es el tercer factor de conversión necesario. Asegúrese de que cada factor de conversión cancela la unidad denominador de su multiplicador a la derecha, y la unidad deseada queda en la respuesta. Los siguientes ejemplos explican estos cálculos.

Ejemplo\(\PageIndex{5}\)

Cuántos gramos de Mg se necesitan para producir 1.01 g de gas H ₂ en esta reacción:\[\ce{Mg(s) + 2HCl(aq) -> MgCl2(aq) + H2(g)^}\nonumber\]

Solución

i. Dado: 1.01 g H _{2 Deseado}:? g Mg.

ii. Masa molar de H ₂ = 2 x1.008 g H.mol ^-1 = 2.016 g H ₂ .mol ^-1, y masa molar = 24.305 g mg.mol ^-1.

iii. La ecuación química se da en el problema.

iv. Las igualdades deseadas: 1 mol Mg = 1 mol H ₂, 1 mol H ₂ = 2.016 g H ₂, 1 mol Mg = 24.305 g Mg

v. Calcular multiplicando la cantidad dada consecutivamente con los tres factores de conversión deseados a partir de las igualdades:

\[1.01 \cancel{\mathrm{~g ~H_{2}}} \times \frac{1 \cancel{\mathrm{~mol} \mathrm{~H}_{2}}}{2.016 \cancel{\mathrm{~g} \mathrm{~H}_{2}}} \times \frac{1 \cancel{\mathrm{~mol} \mathrm{~Mg}}}{1 \cancel{\mathrm{~mol} \mathrm{~H}_{2}}} \times \frac{24.305 \mathrm{~g} \mathrm{~Mg}}{1 \cancel{\mathrm{~mol} \mathrm{~Mg}}}=11.9 \mathrm{~g~Mg}\nonumber\]

Ejemplo\(\PageIndex{6}\)

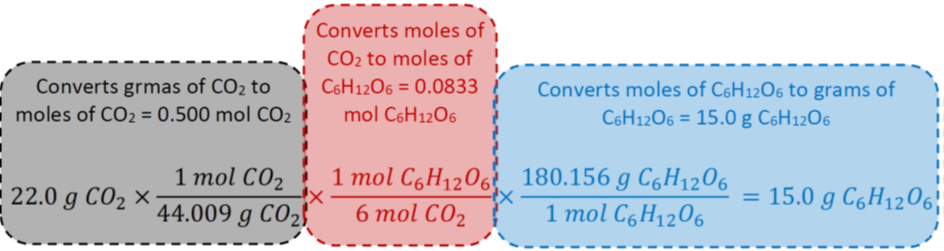
¿Cuántos gramos de glucosa se producen si se consumen 22.0 g de dióxido de carbono en la reacción de fotosíntesis?

Solución

i. Dado: 22.0 g CO _{2 Deseado}:? g C ₆ H ₁₂ O ₆.

ii. Masas molares: de CO ₂ = 1x12.011 g C.mol ^-1 + 2x15.999 g O.mol ^-1 = 44.009 g CO ₂ .mol ^-1, y masa molar de C ₆ H ₁₂ O ₆ = 6x12.011 g C.mol ^-1 + 12x1.008 g H.mol ^-1 + 6x 15.999 g O.mol ^-1 = 180.156 g C ₆ H ₁₂ O ₆ .mol ^-1.

iii. La ecuación química:\(\ce{6CO2 + 6H2O -> C6H12O6 + 6O2}\)

iv. Las igualdades deseadas: 6 mol CO ₂ = 1 mol C ₆ H ₁₂ O ₆, 1 mol CO ₂ = 44.009 g CO ₂, 1 mol C ₆ H ₁₂ O ₆ = 180.156 g C ₆ H ₁₂ O ₆.

v. Calcular multiplicando la cantidad dada consecutivamente con los tres factores de conversión deseados a partir de las igualdades:

\[22.0 \cancel{\mathrm{~g} \mathrm{~CO}_{2}} \times \frac{1 \cancel{\mathrm{~mol} \mathrm{~CO}_{2}}}{44.009 \cancel{\mathrm{~g} \mathrm{~CO}_{2}}} \times \frac{1 \cancel{\mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}}{6 \cancel{\mathrm{~mol} \mathrm{~CO}_{2}}} \times \frac{180.156 \mathrm{~g} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}{1 \cancel{\mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}}=15.0 \mathrm{~g} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}\nonumber\]

La Fig. 4.6.2 ilustra lo que hace cada factor de conversión en el caso del ejemplo anterior número 4.6.5

Mas a cálculo de masa basado en una ecuación química — Figura\(\PageIndex{2}\): Ilustración de la operación de factores de conversión en un cálculo masa-masa basado en una ecuación química equilibrada del ejemplo 4.. 6.6 a pregunta: “calcular gramos de C ₆ H ₁₂ O ₆ producidos a partir de 22.0 g CO ₂ en reacción de fotosíntesis \(\ce{6CO2 + 6H2O -> C6H12O6 + 6O2}\)”.