6.6: El pH
- Page ID
- 77254
¿Qué es el pH?
La acidez de una solución acuosa se relaciona con la concentración de iones H 3 O +, pero hay dos problemas con ella. El primer problema es que la concentración molar de ion hidronio [H 3 O +] varía en un amplio rango, generalmente de 1 a 0.00000000000001 lo cual no es fácil de comprender. La escala logarítmica resuelve el problema, por ejemplo, si un número aumenta de 1 a 1000, aumenta de 0 a 3 en una escala logarítmica a la base 10. El segundo problema es que el [H 3 O +] suele ser un número pequeño entre 0 y 1. El registro de un número que está entre 0 y 1 es un número negativo que no es fácil de captar mentalmente. Si un número está entre 0 y 1, su recíproco es mayor que 1, y su log es un número +ve.
El pH se define como un log de reciprocidad de la concentración molar de iones hidronio [H 3 O +]. También se puede afirmar que el pH es un log negativo de la concentración molar de ion hidronio [H 3 O +]. La forma matemática del pH es la siguiente.
\ begin {ecuación}
p H=\ log\ frac {1} {\ left [\ mathrm {H} _ {3}\ mathrm {O} ^ {+}\ derecha]} =-\ log\ izquierda [\ mathrm {H} _ {3}\ mathrm {O} ^ {+}\ derecha]\ nonumber
\ end {ecuación}
Un pH suele ser un número positivo entre 0 y 14.
Cálculo del pH
Primero, determinar la concentración molar de ión hidronio [H 3 O +]. Que tomar log base 10 de [H 3 O +] y cambiar el signo de la respuesta, es decir:
\ begin {ecuación}
p H=-\ log\ left [\ mathrm {H} _ {3}\ mathrm {O} ^ {+}\ derecha]\ nonumber
\ end {ecuación}
Calcular el pH del agua neutra que tiene [H 3 O +] = 10 -7 M?
Solución
Dado [H 3 O +] = 10 -7 M, pH deseado =?
Fórmula:\(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\)
Conecte los valores y calcule:\(p H=-\log \left(10^{-7}\right)=7.0\)
La secuencia de claves para el cálculo en una calculadora científica de Microsoft Window es (la última casilla es la salida de la secuencia de claves):
El número dado en notación científica es 1 x 10 -7 que tiene una cifra significativa mostrada por la parte de coeficiente del número en negrita. El número de decimales en el número de pH muestra las cifras significativas, es decir, 7. 0 tiene un lugar decimal que se muestra en negrita, lo que significa que tiene una cifra significativa.
¿Calcular el pH de la solución de HCl 0.010 M?
Solución
Dado [HCl] = 0.010 M = [H 3 O +], pH deseado =?
Fórmula:\(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\)
Conecte los valores y calcule:\(p H=-\log (0.010)=2.00\)
La secuencia de claves para el cálculo en una calculadora científica de Microsoft Window es (la última casilla es la salida de la secuencia de claves):
Tenga en cuenta que el número dado 0.0 10 M tiene dos cifras significativas que se muestran en negrita. Entonces, la respuesta pH 2. 00 también tiene dos cifras significativas mostradas en negrita.
¿Calcular el pH de la solución de HCl 0.10 M?
Solución
Dado [HCl] = 0.10 M = [H 3 O +], pH deseado =?
Fórmula:\(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\)
Cálculos:\(p H=-\log (0.10)=1.00\)
A medida que el ácido 0.01M y 0.10M se agrega gradualmente para aumentar el ácido de agua neutra en el ejemplo 1 a 0.01M en el ejemplo 2 a 0.10 M en el ejemplo 3,, el pH disminuyó gradualmente de 7 a 2 a 1.
El pH de la solución ácida es menor a 7. Cuanto más ácida es la solución, menor es el pH.
El pH disminuye a medida que el [H3O+] aumenta debido a que se utiliza el recíproco de [H3O+] en el cálculo del pH. Cuanto mayor sea el número dado, menor es el recíproco; se traduce como “cuanto más ácida es la solución, menor es el pH.
Calcular el pH de la solución de NaOH 0.010 M?
Solución
Dado [NaOH] = 0.010 M = [OH -], pH deseado =?
Primero, calcula [H 3 O +] a partir del dar [OH -]:\(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=10^{-14} /\left[\mathrm{OH}^{-}\right]=10^{-14} / 0.010=1.0 \times 10^{-12}\)
Que calcular el pH:\(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=-\log \left(1.0 \times 10^{-12}\right)=12.00\)
Tenga en cuenta que el número dado 0.0 10 M tiene dos cifras significativas que se muestran en negrita. Entonces, la respuesta pH 12. 00 también tiene dos cifras significativas mostradas en negrita.
Calcular el pH de la solución de NaOH 0.10 M?
Solución
Dado [NaOH] = 0.10 M = [OH -], pH deseado =?
Primero, calcula [H 3 O +] a partir del dar [OH -]:\(10^{-14} /\left[\mathrm{OH}^{-}\right]=10^{-14} / 0.10=1.0 \times 10^{-13}\)
Fórmula: [H 3 O +] = 10 -14/[OH -] = 10 -14 /0.10 = 1.0 x 10 -13.
Que calcular el pH:\(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=-\log \left(1.0 \times 10^{-13}\right)=13.00\)
A medida que la base, 0.010M y 0.10M se agregan gradualmente en los dos exámenes previos al agua neutra a pH 7, el pH aumenta de 7 a 12 a 13.
El pH de la solución básica es superior a 7. Cuanto más básica es la solución, mayor es el pH.
Medición de pH
El pH se suele medir en laboratorios mediante medidores digitales de pH. El electrodo del medidor de pH se calibra primero con soluciones de valores de pH conocidos, y luego el electrodo se sumerge en la solución de prueba para leer su valor de pH. Hay disponibles papeles indicadores de pH universales que se vuelven a un color específico cuando se colocan en la solución. El pH se lee haciendo coincidir el color del papel de prueba con el color de la tabla. La Fig. 6.6.1 muestra un medidor de pH digital y dos papeles indicadores de pH universales comúnmente utilizados para mediciones de pH en laboratorios.
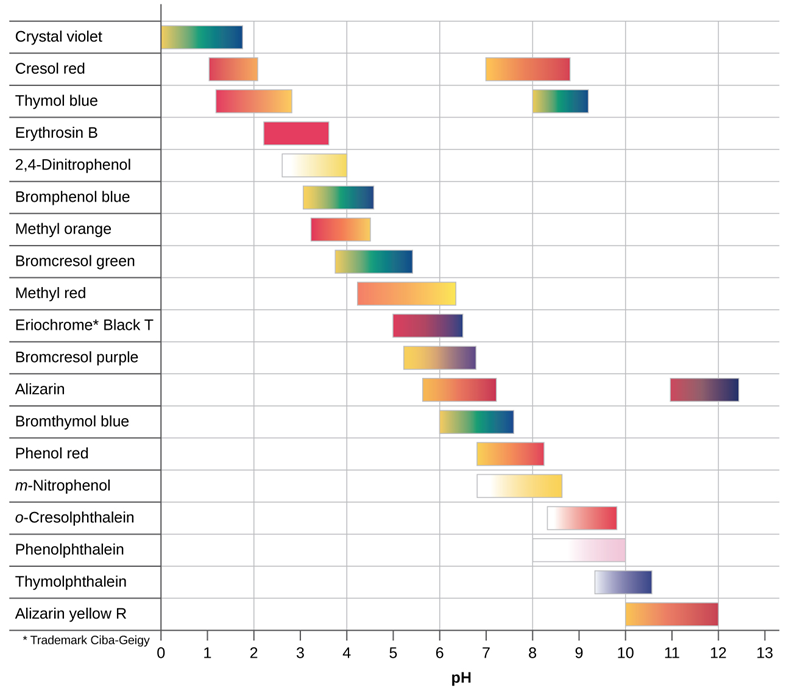
Los indicadores de pH son ácidos débiles o bases débiles que cambian de color en un rango de pH específico. Se agregan unas gotas de la solución de un papel indicador de pH a la solución de prueba en la que se cambia el pH mediante la adición de ácido o base. El cambio en el color de la solución indica el rango de pH en el que el indicador cambia el color. La Figura 6.6.2 muestra los colores y los rangos de transición de color de algunos de los indicadores de pH comunes.
Cálculo de la concentración de iones hidronio a partir
La fórmula para calcular la concentración molar de iones hidronio [H 3 O +] se obtiene reordenando la fórmula de pH. \(p H=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\), reorganiza para:\(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\operatorname{antilog}(-p H)=10^{-p H}\).
Calcular [H 3 O +] de una muestra de orina que tiene pH 7.56?
Solución
Dado: pH = 7.56, Deseado: [H 3 O +] =?
Fórmula:\(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=10^{-p H}\).
Enchufe los valores y calcule:\(\left[H_{3} O^{+}\right]=10^{-p H}=10^{-(7.56)}=2.8 \times 10^{-8} M\)
La secuencia de claves para el cálculo en una calculadora científica de Microsoft Window es (la última casilla es la salida de la secuencia de claves):
La respuesta calculada en el ejemplo anterior es un número largo, pero se redondea a dos cifras significativas que se muestran en negrita en 2.8\(\times 10^{-8} M\), debido a que el número dado pH 7. 56 tiene dos cifras significativas mostradas en negrita.
Importancia de la Escala de pH
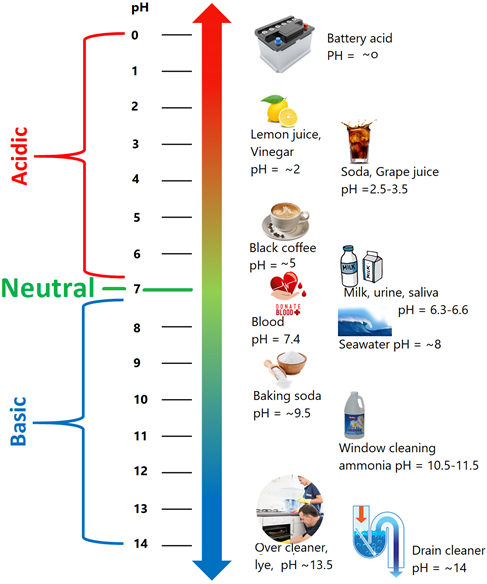
La escala de pH varía de ~0 a ~14. El pH de 7 es neutro, el pH superior a 7 es básico y el pH inferior a 7 es ácido, como se ilustra en la Fig. 6.6.3. Los diferentes alimentos tienen diferentes valores de pH, como se muestra en la Fig. 6.1.1. De igual manera, varios de los ácidos y bases en uso doméstico tienen un rango de pH específico, como se muestra en la Fig. 6.6.3.
El control del pH es esencial en el buen funcionamiento de los sistemas biológicos. Las plantas prosperan si el suelo no tiene un pH demasiado ácido o demasiado básico. Las carencias y los revers tienen un rango específico de pH en el que la vida acuática puede sobrevivir. El agua natural estadounidense tiene un pH en el rango de 6.5 a 8.5. El agua de mar tiene un rango estrecho específico de pH 7.5 a pH 8.4 en el que la vida en el mar puede funcionar correctamente.
El pH de los fluidos corporales
Los fluidos corporales humanos varían en pH, como se muestra en la Fig. 6.6.4. La saliva en la boca es ligeramente ácida, pero el estómago tiene el pH más bajo del cuerpo. El pH fuertemente ácido en el estómago ayuda a digerir algunos alimentos, y también ayuda a matar las bacterias que pueden ingresar al estómago a través de los alimentos. Cuando el alimento ingresa al intestino grueso, el pH cambia a básico lo que ayuda a digerir los alimentos que no pudieron ser digeridos en el ambiente ácido del estómago. El pH cambia a más básico en el intestino delgado.
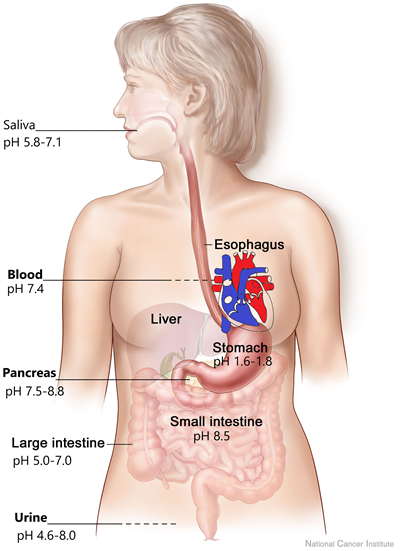
La sangre tiene un pH de 7.4, y puede variar en un pequeño rango de 7.35 a 7.45. Si el pH de la sangre sale del rango de 7.35 a 7.45 puede resultar en problemas médicos. Las enzimas en el cuerpo necesitan un rango de pH específico porque los enlaces de hidrógeno juegan un papel vital en las estructuras necesarias para un correcto funcionamiento. Los cambios de pH afectan los enlaces de hidrógeno y pueden hacer que las enzimas sean menos activas o pueden inactivarlas. El pH de la sangre se mantiene mediante una acción compleja de tampones que se describen en las secciones posteriores. El pH de la orina puede variar en un amplio rango de 4.6 a 8, dependiendo de la dieta y ejercicios recientes.
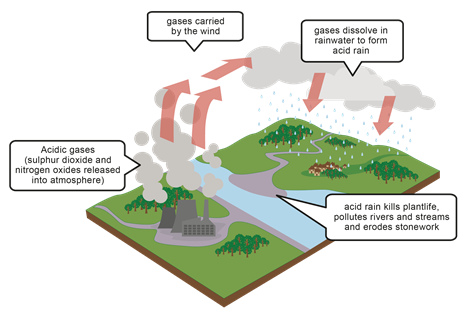
Lluvia ácida
Los gases ácidos como NO, NO 2, N 2 O 4, SO 2 se liberan al ambiente principalmente durante la combustión de combustibles fósiles. Estos gases se disuelven en el agua de lluvia y hacen que la lluvia sea ácida. Por ejemplo, el dióxido de azufre se disuelve en agua y hace que el ácido sulfuroso:
\[\mathrm{SO}_{2}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{I}) \rightleftarrows \mathrm{H}_{2} \mathrm{SO}_{3}(\mathrm{aq})\nonumber\]
La lluvia ácida daña el medio ambiente al hacer que el suelo, el agua del río y el agua carente sean ácidos. El suelo ácido y el agua, a su vez, afectan a las plantas y a la vida acuática. El agua ácida también reacciona con el carbonato de calcio y corroe los metales que son responsables del daño a la escultura y otras estructuras, como se ilustra en la Fig. 6.6.5, Fig. 6.6.6 y Fig. 6.6.7.
