1.4: Unidad 3: Barra sinusoidal
- Page ID
- 153541
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivo
Después de completar esta unidad, deberías ser capaz de:
- Entender el principio de la barra sinusoidal.
- Explica cómo usar una barra sinusoidal correctamente.
- Comprender los bloques de calibre deslizante y el escurrido.
- Calcular la altura del bloque de calibre.
La barra sinusoidal
Una barra sinusoidal se utiliza junto con bloques de calibre deslizante para una medición angular precisa. Una barra sinusoidal se utiliza ya sea para medir un ángulo con mucha precisión o ubicar la cara cualquier trabajo a un ángulo dado. Las barras sinusoidales están hechas de acero resistente a la corrosión con alto contenido de cromo y están endurecidas, rectificadas de precisión y estabilizadas.

Figura 1. La barra sinusoidal
Dos cilindros de igual diámetro se colocan en los extremos de la barra. Los ejes de estos dos cilindros son mutuamente paralelos entre sí, y también son paralelos a, y a igual distancia de, la superficie superior de la barra sinusoidal. Se puede obtener una precisión de hasta 0.01mm/m de longitud de la barra sinusoidal.
Una barra sinusoidal se usa generalmente con bloques de calibre deslizante. La barra sinusoidal forma la hipotenusa de un triángulo rectángulo, mientras que los bloques de calibre deslizante forman el lado opuesto. La altura del bloque de calibre deslizante se encuentra multiplicando el seno del ángulo deseado por la longitud de la barra sinusoidal: H = L * sin (θ).
Por ejemplo, para encontrar la altura del bloque de calibre para un ángulo de 13˚ con una barra sinusoidal de 5.000″, multiplica el pecado (13˚) por 5.000″: H = 5.000″ * sin (13˚). Los bloques de calibre deslizante apilados a una altura de 1.124″ se usarían entonces para elevar la barra sinusoidal al ángulo deseado de 13˚.
Principios de barra sinusoidal
- La aplicación de trigonometría se aplica al uso de barra sinusoidal.
- Se utilizan una placa de superficie, una barra sinusoidal y medidores de deslizamiento para la formación precisa de un ángulo.
- Es posible configurar cualquier ángulo θ usando la longitud estándar del lado AB, y calculando la altura del lado BC usando BC = AB * sin (θ).
- El ángulo θ viene dado por θ = asin (BC/AB).
- La Figura 1 muestra una barra sinusoidal típica montada sobre una placa superficial con bloques de calibre deslizante de la altura requerida BC para formar un ángulo deseado θ.
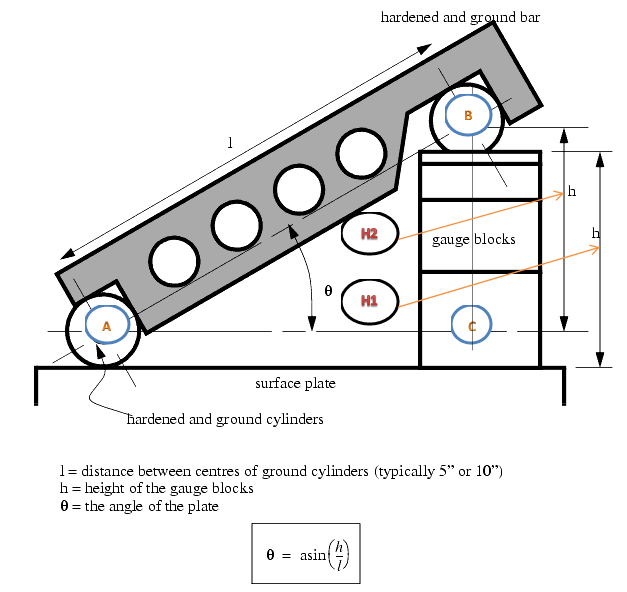
Figura 2: Formando un ángulo con una barra sinusoidal y bloques calibradores
Escursión
El término escurrido se refiere a una condición de contacto íntimo y completo por adherencia apretada entre caras de medición. El escurrido se realiza a mano mediante movimientos de deslizamiento y torsión. Un manómetro se coloca perpendicular a otro usando presión de medición estándar y luego se aplica un movimiento giratorio hasta que los bloques se alinean. De esta manera se expulsa aire de entre las caras del calibre haciendo que los bloques se adhieran. Esta adherencia es causada parcialmente por la atracción molecular y parcialmente por la presión atmosférica. De manera similar, para separar calibres de deslizamiento, se debe utilizar un movimiento combinado de deslizamiento y torsión.
1. Para establecer un ángulo en cualquier barra sinusoidal, primero debe determinar la distancia central de la barra sinusoidal (C), el ángulo que desea establecer (A) y si el ángulo está en grados-minutos-segundos o grados decimales.
2. A continuación, ingrese esa información en las áreas de entrada correspondientes a continuación. Utilice un punto decimal para el separador, ya sea que el ángulo esté en grados-minutos-segundos o grados decimales.
3. Pulsa el botón 'Calcular' y luego ensambla una pila de bloques de calibre (G) para igualar el tamaño que se devuelve. Las unidades de la pila coincidirán con las unidades de la distancia central (es decir, Si ingresa la distancia central como 5 para una placa sinusoidal de 5 pulgadas, la pila de bloques de calibre también estará en pulgadas).
4. Coloque estos bloques de medidores de deslizamiento debajo del rollo de bloque de calibre del dispositivo sinusoidal y se establece el ángulo deseado.
5. Aprieta el mecanismo de bloqueo en aquellos dispositivos que tienen uno y ya está listo para comenzar.
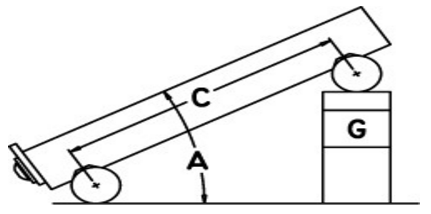
Figura 3: Utiliza la fórmula: G = C * Sin (A)
Si solo quieres establecer un ángulo con una barra sinusoidal y pila de bloques, entonces toma el seno del ángulo deseado en tu calculadora y multiplica el resultado por la distancia entre los centros de los cilindros en la barra sinusoidal. Armar una pila de bloques igual a este valor y ponerla debajo de uno de los cilindros.
Cálculo de configuración de la barra
Para calcular la altura del bloque de calibre necesaria para configurar una barra sinusoidal a un ángulo específico, todo lo que tienes que hacer es tomar el SIN del ángulo y multiplicarlo por la longitud de la barra sinusoidal. La longitud de la barra sinusoidal es la distancia entre los centros de los pasadores de calibre de barra sinusoidal.
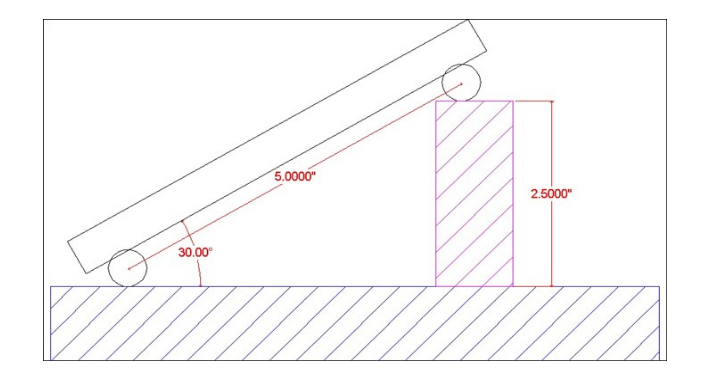
Figura 4. Barra sinusoidal
Ejemplo:
Configure una barra sinusoidal de 5.0” o una placa sinusoidal a 30°
SIN (30˚) = 0.5000
0.5000 x 5.0″ (Longitud de la barra sinusoidal) = 2.5000″
Redondear 2.5000″ a 4 Decimales = 2.5000″ Altura del Bloque Calibre.
Tabla 1 Ángulos y alturas comunes para una barra sinusoidal de 5 pulgadas:
| Ángulo | Altura |
|---|---|
| 5° | 0.4358″ |
| 10° | 0.8682″ |
| 15° | 1.2941″ |
| 20° | 1.7101″ |
| 25° | 2.1131″ |
| 30° | 2.5000″ |
| 35° | 2.8679″ |
| 40° | 3.2139″ |
| 45° | 3.5355″ |
| 50° | 3.8302″ |
| 55° | 4.0958″ |
| 60° | 4.3301″ |
Uso de barra sinusoidal
Para medir un ángulo conocido o ubicar cualquier trabajo en un ángulo dado:
- Siempre use una placa de superficie perfectamente plana y limpia.
- Coloque un rodillo en la placa de superficie y el otro rodillo en la pila de bloques de calibre deslizante de altura H.
- Deje que la barra sinusoidal se establezca en un ángulo θ.
- Entonces sin (θ) = H/L, donde L es la distancia entre el centro.
- Conociendo así θ, H se puede encontrar y cualquier trabajo se puede establecer en este ángulo ya que la cara superior de la barra sinusoidal está inclinada en un ángulo θ con respecto a la placa superficial.
- Para un mejor resultado ambos rodillos deben colocarse sobre un bloque de calibre deslizante de altura H1 y H2 respectivamente. Véase la figura anterior,
- ??? ? = (?? −??) /L
PRUEBA UNITARIA
- Describir el uso de la barra sinusoidal.
- Calcule la elevación requerida de la barra sinusoidal para el ángulo de 37˚.
- Una barra sinusoidal de 5.00” es elevada 1.50”. Calcular el ángulo.
- Determine la elevación para 30˚ usando barra sinusoidal de 5.00”.
- Determine la elevación para 42˚ usando barra sinusoidal de 5.00”.
- Una barra sinusoidal de 5.00” es elevada 1.25”. ¿Qué ángulo se establece?
- ¿Qué pila de bloques de calibre establecería un ángulo de 35˚ usando una barra sinusoidal de 5.00”?

